OpenCV C++案例实战二十七《角度测量》
前言
本案例通过使用OpenCV中的鼠标点击事件进行物体角度测量。以鼠标点击三点确定一个角度。第一个点:即为需要测量角度所在位置点(中心点),第二、三点确定角度。
一、鼠标响应事件
原图如图所示:
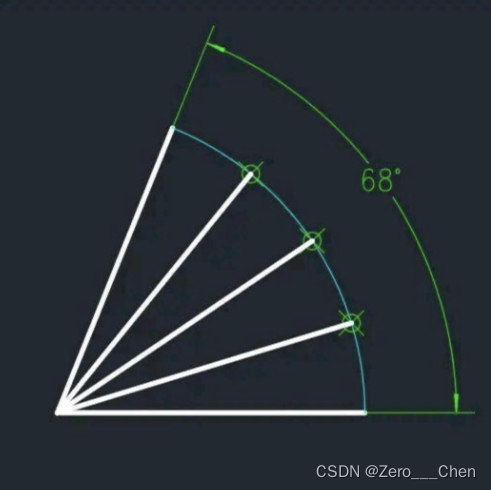
首先第一步,利用鼠标响应事件进行取点操作。OpenCV中的setMouseCallback可以完成此操作。参数也比较简单。
void setMouseCallback(
const String& winname, //窗口名称
MouseCallback onMouse, //响应回调函数
void* userdata = 0 //用户传入数据,可选
);
1.1功能源码
具体请看源码实现
//利用鼠标响应事件进行取点
void DrawCircle(int event, int x, int y, int flags, void* userdata)
{
//鼠标左键点击,记录并绘制圆点
/*
鼠标点击三点确定一个角度。第一个点:即为需要测量角度所在位置点(中心点);第二、三个点:确定角度
*/
Mat canvas = *((Mat*)userdata); //传入图像
if (event == EVENT_LBUTTONDOWN)
{
if (x > 0 && y > 0)
{
point.x = x; //当鼠标左键点击时,记录鼠标点击位置
point.y = y;
}
}
if (event == EVENT_LBUTTONUP)
{
//当鼠标左键抬起时,保存鼠标点击坐标位置
clickcount++; //点击次数+1
myPoints.push_back(point);
circle(canvas, point, 5, Scalar(0, 0, 255), -1);//绘制点
putText(canvas, to_string(clickcount), Point(point.x-10,point.y-10), FONT_HERSHEY_SIMPLEX, 1, Scalar(0, 0, 255), 3);
imshow("Demo", canvas);
}
}
1.2功能效果
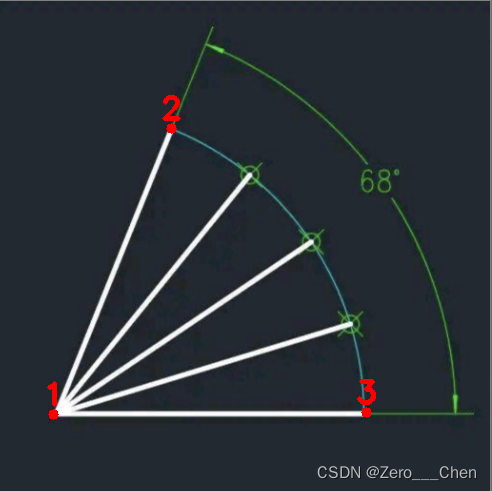
二、计算直线角度
2.1 计算直线斜率
根据直线起始点计算直线斜率。k=(y2-y1) / (x2-x1)
//计算直线斜率
double gradient(Point2f pt1, Point2f pt2)
{
if (pt1.x == pt2.x)
{
return 9999999.9; //斜率不存在
}
else
{
return (pt2.y - pt1.y) / (pt2.x - pt1.x);
}
}
根据传入的三个点,我们可以分别计算出两条直线的斜率,分别是k1,k2。
2.2计算直线角度
两直线角度公式如下:tanθ=|(k1-k2)/ (1+k1*k2) |

此时,我们计算出来的θ还是弧度,我们需要把它转为角度制。
弧度与角度转换公式为:
1° = π / 180 ≈ 0.01745 rad
1 rad = 180 / π = 57.30°
所以我们最终的角度为: Angle = θ*180 / π
2.3功能源码
//计算两直线所成角度
double getAngle(vector<Point2f>myPoints, Point2f &ArcCenter, Point2f &StartPoint, Point2f &EndPoint)
{
ArcCenter = myPoints[0];//中心点,确定需要测量哪个角
StartPoint = myPoints[1];//起点
EndPoint = myPoints[2];//终点
//两直线斜率
double k1 = gradient(StartPoint, ArcCenter);
double k2 = gradient(EndPoint, ArcCenter);
//弧度
double theta = atan(abs((k2 - k1) / (1 + k1 * k2)));
//角度
double Angle = theta * 180 / CV_PI;
return Angle;
}
三、绘制圆弧
至此我们已经完成了取点、角度计算工作。为了效果显示,这里,我们将三点形成的角度用圆弧绘制出来。
这里我贴出某点绕原点旋转θ角度后坐标位置推到过程。

类似的,我们可以推导出,平面中某一点绕任意点旋转θ角度后坐标
平面中,一点(x,y)绕任意点(dx,dy)逆时针旋转θ角度后坐标位置:
x1 = dx + (x-dx)cos(θ) - (y-dy)sin(θ)
y1 = dy + (x-dx)sin(θ) + (y-dy)cos(θ)
平面中,一点(x,y)绕任意点(dx,dy)顺时针旋转θ角度后坐标位置:
x1 = dx + (x-dx)cos(-θ) - (y-dy) sin(-θ)
y1 = dy + (x-dx)sin(-θ) + (y-dy)cos(-θ)
3.1功能源码
//绘制圆弧
void DrawArc(Mat src, Point2f& ArcCenter, Point2f& StartPoint, Point2f& EndPoint, double &angle)
{
double Angle1 = atan2((StartPoint.y - ArcCenter.y), (StartPoint.x - ArcCenter.x));//起始弧度
double Angle2 = atan2((EndPoint.y - ArcCenter.y), (EndPoint.x - ArcCenter.x));//终止弧度
double Angle = Angle2 - Angle1;//总弧度
Angle = Angle * 180.0 / CV_PI;//弧度转角度
if (Angle < 0) Angle = 360 + Angle;
if (Angle == 0) Angle = 360;
int ArcLength = floor(Angle / 1); // 向下取整
vector<Point2f> ArcPoints;//取出所有圆弧上的点
for (int i = 0; i < ArcLength; i++)
{
//每隔一度取一个点
double SinTheta = sin(i * CV_PI / 180);
double CosTheta = cos(i * CV_PI / 180);
double x = ArcCenter.x + CosTheta * (StartPoint.x - ArcCenter.x) - SinTheta * (StartPoint.y - ArcCenter.y);
double y = ArcCenter.y + SinTheta * (StartPoint.x - ArcCenter.x) + CosTheta * (StartPoint.y - ArcCenter.y);
ArcPoints.push_back(Point2f(x, y));
}
//绘制圆弧
for (int i = 0; i < ArcPoints.size() - 1; i++)
{
line(src, Point(ArcPoints[i]), Point(ArcPoints[(i + 1)]), Scalar(0, 255, 0), 2);
}
line(src, Point(ArcCenter), Point(StartPoint), Scalar(0, 255, 0), 2);
line(src, Point(ArcCenter), Point(EndPoint), Scalar(0, 255, 0), 2);
putText(src, to_string(angle), EndPoint, FONT_HERSHEY_SIMPLEX, 1, Scalar(0, 255, 0), 2);
}
四、结果显示
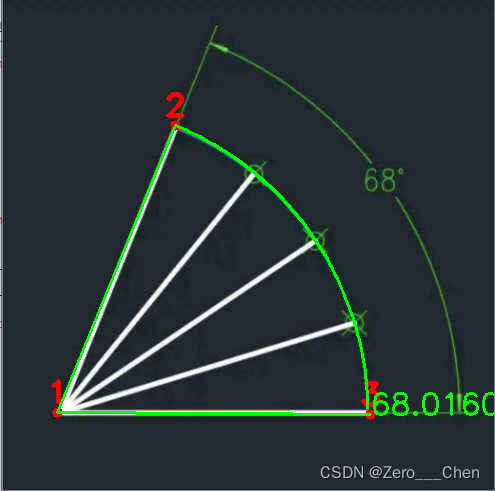

五、源码
具体功能实现请看源码,有不清楚的地方可私信我。。
#include<iostream>
#include<opencv2/opencv.hpp>
#include<math.h>
using namespace std;
using namespace cv;
Point2f point(-1, -1);//初始化鼠标点击坐标
vector<Point2f>myPoints;//将鼠标点击到的坐标存入vector,作为全局变量
int clickcount = 0;//记录鼠标点击次数
//利用鼠标响应事件进行取点
void DrawCircle(int event, int x, int y, int flags, void* userdata)
{
//鼠标左键点击,记录并绘制圆点
/*
鼠标点击三点确定一个角度。第一个点:即为需要测量角度所在位置点(中心点);第二、三个点:确定角度
*/
Mat canvas = *((Mat*)userdata); //传入图像
if (event == EVENT_LBUTTONDOWN)
{
if (x > 0 && y > 0)
{
point.x = x; //当鼠标左键点击时,记录鼠标点击位置
point.y = y;
}
}
if (event == EVENT_LBUTTONUP)
{
//当鼠标左键抬起时,保存鼠标点击坐标位置
clickcount++; //点击次数+1
myPoints.push_back(point);
circle(canvas, point, 5, Scalar(0, 0, 255), -1);//绘制点
putText(canvas, to_string(clickcount), Point(point.x-10,point.y-10), FONT_HERSHEY_SIMPLEX, 1, Scalar(0, 0, 255), 3);
imshow("Demo", canvas);
}
}
//计算直线斜率
double gradient(Point2f pt1, Point2f pt2)
{
if (pt1.x == pt2.x)
{
return 9999999.9; //斜率不存在
}
else
{
return (pt2.y - pt1.y) / (pt2.x - pt1.x);
}
}
//计算两直线所成角度
double getAngle(vector<Point2f>myPoints, Point2f &ArcCenter, Point2f &StartPoint, Point2f &EndPoint)
{
ArcCenter = myPoints[0];//中心点,确定需要测量哪个角
StartPoint = myPoints[1];//起点
EndPoint = myPoints[2];//终点
//两直线斜率
double k1 = gradient(StartPoint, ArcCenter);
double k2 = gradient(EndPoint, ArcCenter);
//弧度
double theta = atan(abs((k2 - k1) / (1 + k1 * k2)));
//角度
double Angle = theta * 180.0 / CV_PI;
return Angle;
}
//绘制圆弧
void DrawArc(Mat src, Point2f& ArcCenter, Point2f& StartPoint, Point2f& EndPoint, double &angle)
{
double Angle1 = atan2((StartPoint.y - ArcCenter.y), (StartPoint.x - ArcCenter.x));//起始弧度
double Angle2 = atan2((EndPoint.y - ArcCenter.y), (EndPoint.x - ArcCenter.x));//终止弧度
double Angle = Angle2 - Angle1;//总弧度
Angle = Angle * 180.0 / CV_PI;//弧度转角度
if (Angle < 0) Angle = 360 + Angle;
if (Angle == 0) Angle = 360;
int ArcLength = floor(Angle / 1); // 向下取整
vector<Point2f> ArcPoints;//取出所有圆弧上的点
for (int i = 0; i < ArcLength; i++)
{
//每隔一度取一个点
double SinTheta = sin(i * CV_PI / 180);
double CosTheta = cos(i * CV_PI / 180);
double x = ArcCenter.x + CosTheta * (StartPoint.x - ArcCenter.x) - SinTheta * (StartPoint.y - ArcCenter.y);
double y = ArcCenter.y + SinTheta * (StartPoint.x - ArcCenter.x) + CosTheta * (StartPoint.y - ArcCenter.y);
ArcPoints.push_back(Point2f(x, y));
}
//绘制圆弧
for (int i = 0; i < ArcPoints.size() - 1; i++)
{
line(src, Point(ArcPoints[i]), Point(ArcPoints[(i + 1)]), Scalar(0, 255, 0), 2);
}
line(src, Point(ArcCenter), Point(StartPoint), Scalar(0, 255, 0), 2);
line(src, Point(ArcCenter), Point(EndPoint), Scalar(0, 255, 0), 2);
putText(src, to_string(angle), EndPoint, FONT_HERSHEY_SIMPLEX, 1, Scalar(0, 255, 0), 2);
}
int main()
{
Mat src = imread("src.jpg");
if (src.empty())
{
cout << "can not read the image..." << endl;
system("pause");
return-1;
}
while (true)
{
imshow("Demo", src);
namedWindow("Demo", WINDOW_AUTOSIZE);
setMouseCallback("Demo", DrawCircle, &src);
if (clickcount == 3)
{
Point2f ArcCenter, StartPoint, EndPoint;
double Angle = getAngle(myPoints, ArcCenter, StartPoint, EndPoint);
DrawArc(src, ArcCenter, StartPoint, EndPoint, Angle);
myPoints.clear();//当完成一次测量后,重置数据
clickcount = 0;
}
char key = waitKey(1);
if (key == 'c')
{
//按c键则重新加载图像
src = imread("src.jpg");
}
else if (key == 27)
{
//按esc键退出程序
break;
}
}
destroyAllWindows();
system("pause");
return 0;
}
总结
本文使用OpenCV C++ 进行物体角度测量,主要操作有以下几点。
1、利用鼠标响应事件取点,三点确定一个角度
2、利用两直线角度公式计算直线角度,注意弧度转角度
3、绘制圆弧,便于显示。注意某一点绕任意点旋转θ角度后的坐标计算公式。