目录

1、回归定义
Regression(回归)就是找到一个函数 functionfunction ,通过输入特征 或者特征系列xx,输出一个数值 ScalarScalar。
例子:Pokemon精灵攻击力预测(Combat Power of a pokemon):
输入:进化前的CP值、物种(Bulbasaur)、血量(HP)、重量(Weight)、高度(Height)
输出:进化后的CP值
2、模型步骤
2.1、模型假设 - 线性模型
2.2.1、一元线性模型(单个特征)
以一个特征 x c p x_{cp} xcp?为例,线性模型假设 ? y = b + w ? x c p \ y = b + w·x_{cp} ?y=b+w?xcp?,所以 w w w和 b b b可以猜测很多模型。x表示输入的对象,下标cp表示对象的一个特征。
2.2.2、多元线性模型(多个特征)
输入多个特征,例如,进化前的CP值、物种(Bulbasaur)、血量(HP)、重量(Weight)、高度(Height)等,特征会有很多。
由此,假设模型为:
线性模型 Linear model:
y
=
b
+
∑
w
i
x
i
y = b + \sum w_ix_i
y=b+∑wi?xi?
?
x
i
x_i
xi?:就是各种特征(fetrure)
x
c
p
,
x
h
p
,
x
w
,
x
h
,
?
?
?
x_{cp}, x_{hp}, x_w, x_h,···
xcp?,xhp?,xw?,xh?,???
w
i
w_i
wi?:各个特征的权重(weight)
w
c
p
,
w
h
p
,
w
w
,
w
h
,
?
?
w_{cp},w_{hp},w_w,w_h,··
wcp?,whp?,ww?,wh?,??
b
b
b:偏移量(bias)

2.2、模型评估 - 损失函数
手机训练数据,共十组数据,定义 x 1 x^1 x1是进化前的CP值, y ^ 1 \hat{y}^1 y^?1进化后的CP值, ^ \hat{} ^ 所代表的是真实值每一个点 ( x c p n , y ^ n ) (x_{cp}^n,\hat{y}^n) (xcpn?,y^?n),对应着进化前的CP值和进化后的CP值。
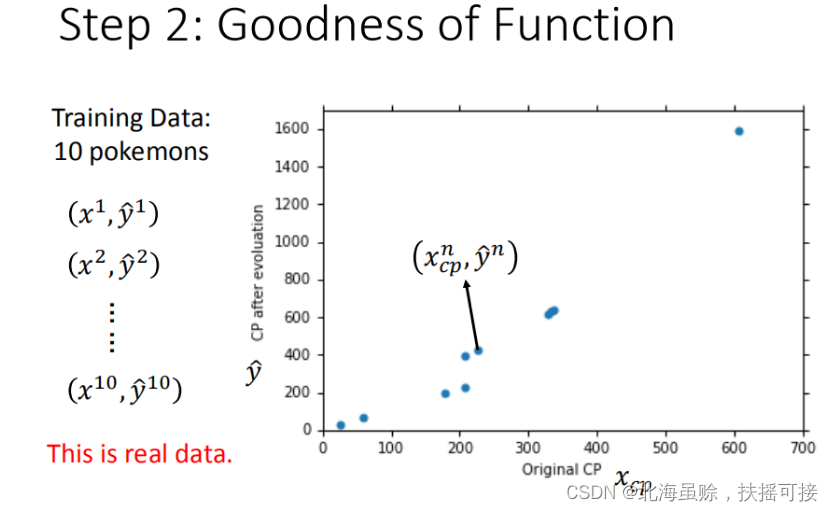
使用损失函数(Loss function)来衡量模型的好坏,统计10组数据真实值与预测值差值平方和
(
y
^
n
?
f
(
x
c
p
n
)
)
2
(\widehat{y}^{n}-f(x_{cp}^{n}))^{2}
(y
?n?f(xcpn?))2的和,和越小模型越好。

寻求最小的损失函数(Loss function)对应的(w,b)。
2.3、最佳模型 - 梯度下降
已知损失函数 L ( w , b ) = ∑ n = 1 10 ( y ^ n ? ( b + w ? x c p ) ) 2 L(w,b)= \sum _{n=1}^{10}(\widehat{y}^{n}-(b+w \cdot x_{cp}))^{2} L(w,b)=∑n=110?(y ?n?(b+w?xcp?))2,寻找 w ? , b ? = a r g min ? L ( w , b ) w^{*},b^{*}=arg \min L(w,b) w?,b?=argminL(w,b)
2.3.1、单变量寻优
定义
w
?
=
a
r
g
min
?
i
n
L
(
w
)
w^{*}=arg \min inL(w)
w?=argmininL(w),通过梯度下降寻找到关于w的局部最优解(非全局最优,寻找的点为极值非最值)
下图中
w
0
w^0
w0为随机选取初始点;
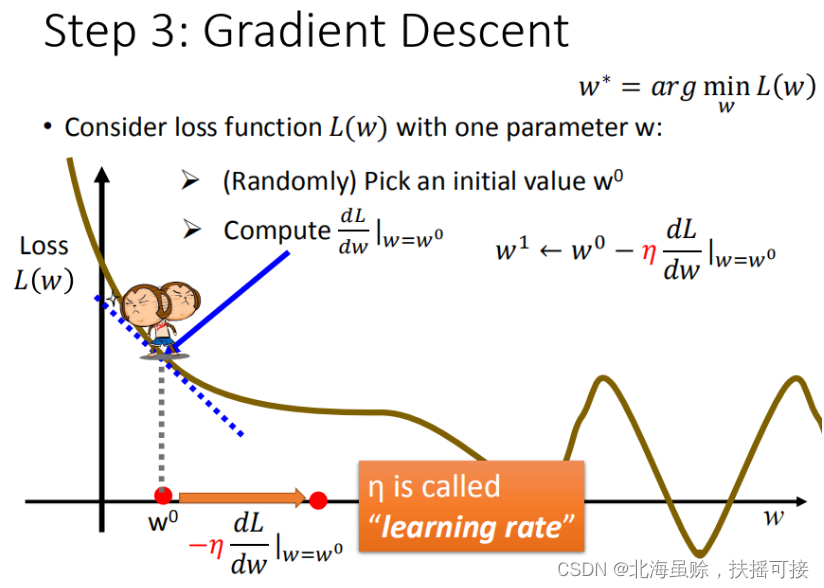
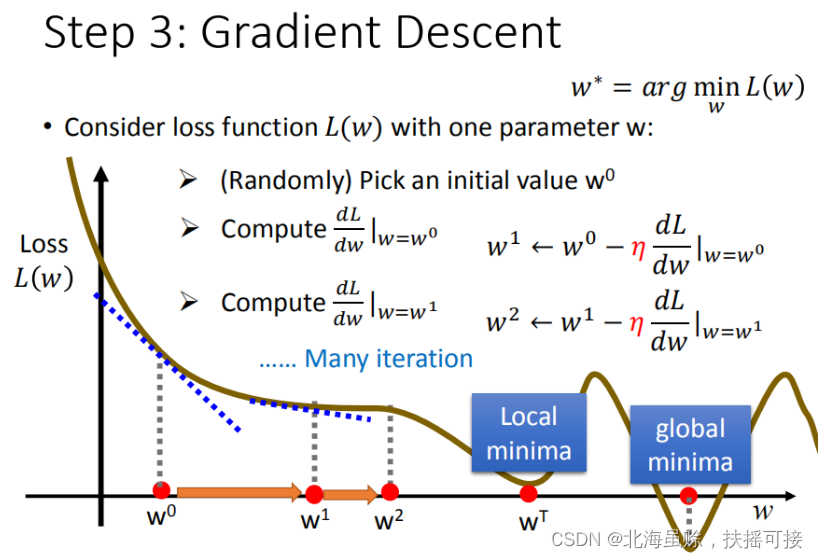
2.3.2、多变量寻优
引入多个模型参数,求偏微分:

优化过程可视化:
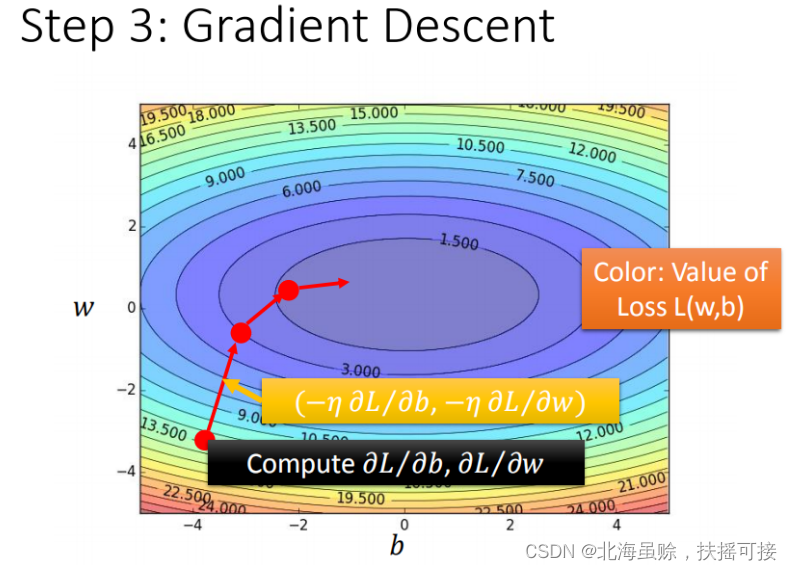
可能存在的问题:
梯度消失;
梯度爆炸…
3、模型验证与检验
使用训练集和测试集的平均误差来验证模型的好坏 我们使用将10组原始数据,训练集求得平均误差为31.9,如图所示:
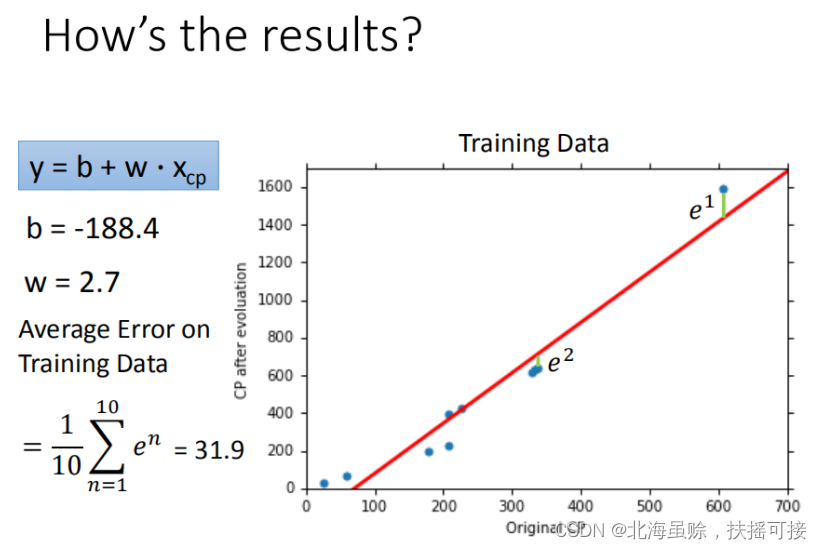
然后再使用10组Pokemons测试模型,测试集求得平均误差为35.0 如图所示:
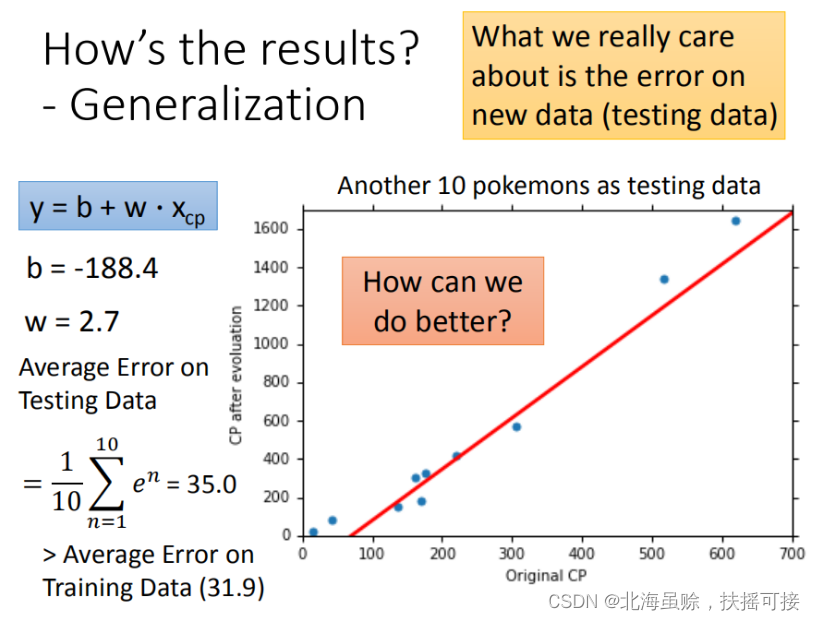
(本人认为使用测试集来验证模型结果,有一点奇怪,但是在本文中,却又比较合理,因为没有具体区分测试集与验证集)
增加模型阶数,会发现出现**过拟合(overfitting)**情况:
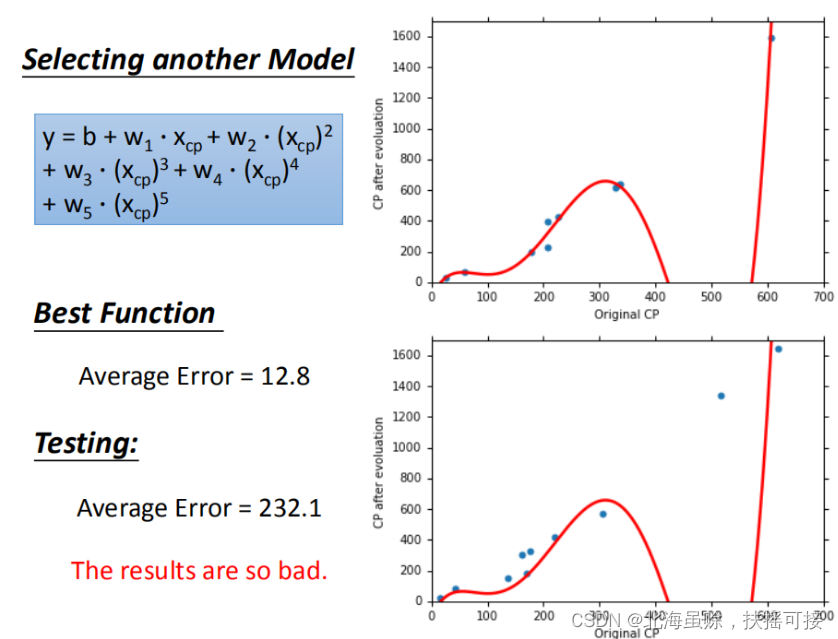
在训练集上面表现更为优秀的模型,为什么在测试集上效果反而变差了?这就是模型在训练集上过拟合的问题。
4、优化模型
通过修改模型处理对象数目来优化模型。例如,Pokemons种类是隐藏得比较深得特征,不同Pokemons种类影响了进化后的CP值的结果。
4.1、四个种类的二元线性模型是合并到一个线性模型中
通过对 Pokemons种类 判断,将 4个线性模型 合并到一个线性模型中
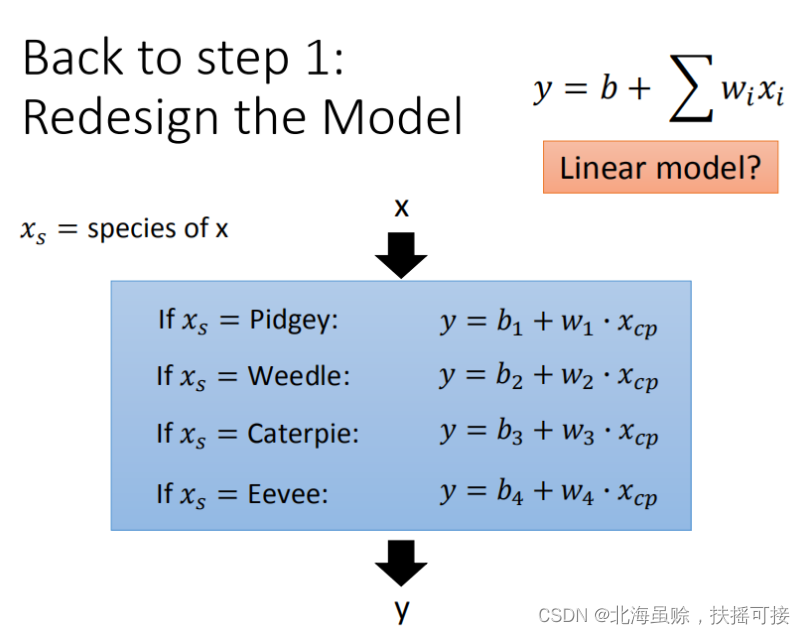
或者转化为合并形式,(引入冲击函数(激活函数))
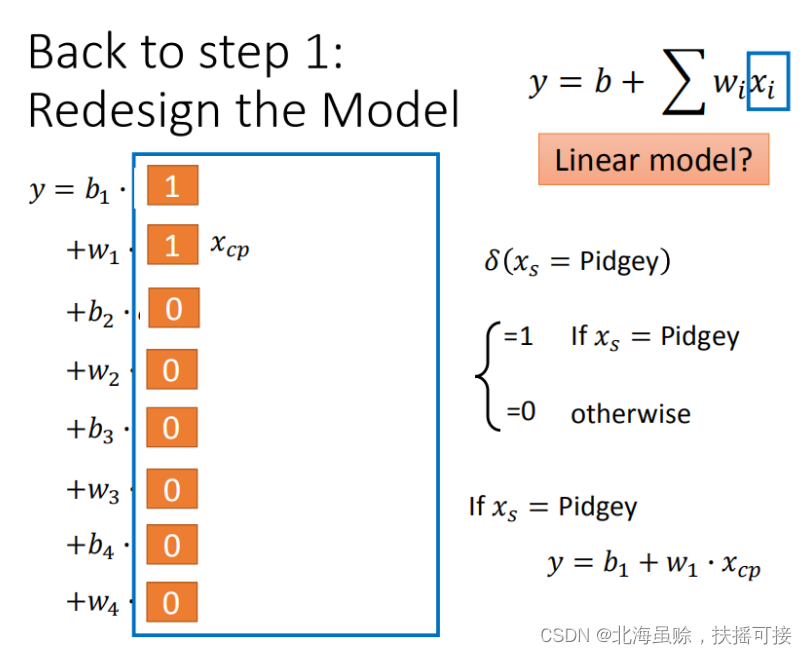
优化结果:
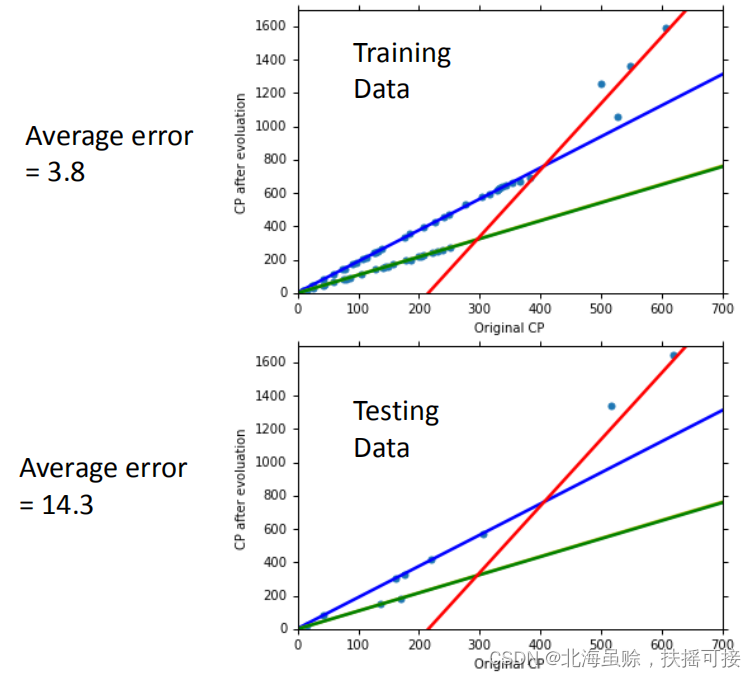
4.2、多输入特征分析(放大招)
如果希望模型更强大表现更好(更多参数,更多input),将血量(HP)、重量(Weight)、高度(Height)也加入到模型中。
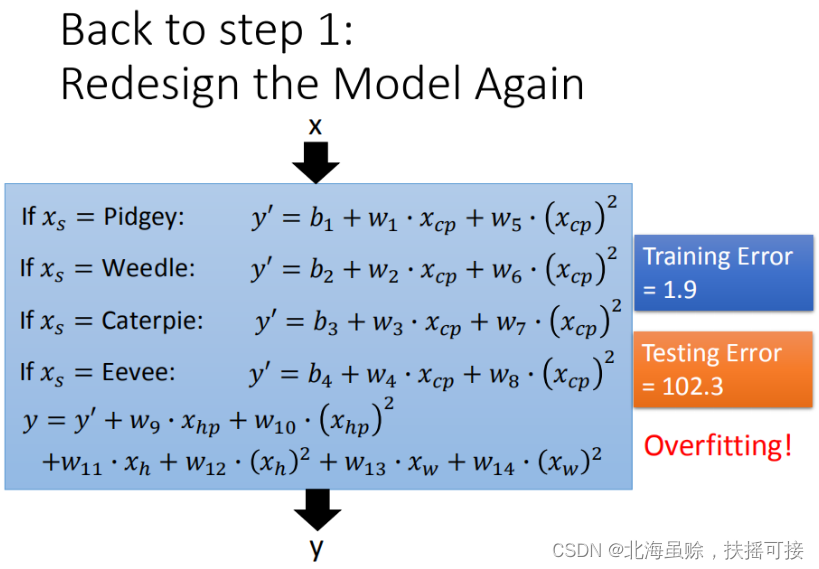
更多特征,更多input,数据量没有明显增加,仍旧导致overfitting。在上图中,可以看出模型默认
x
c
p
x_{cp}
xcp? 是与种类有关,而其他特征与种类无关,(可能是个小BUG,不过完善了肯定继续过拟合)。
4.3、加入正则化(平滑操作)
更多特征,但是权重 ww 可能会使某些特征权值过高,仍旧导致overfitting,所以加入正则化。正则化可以通过调整模型的倾斜程度,调整模型对于噪声的敏感度。

不同正则项的验证与测试结果如下:
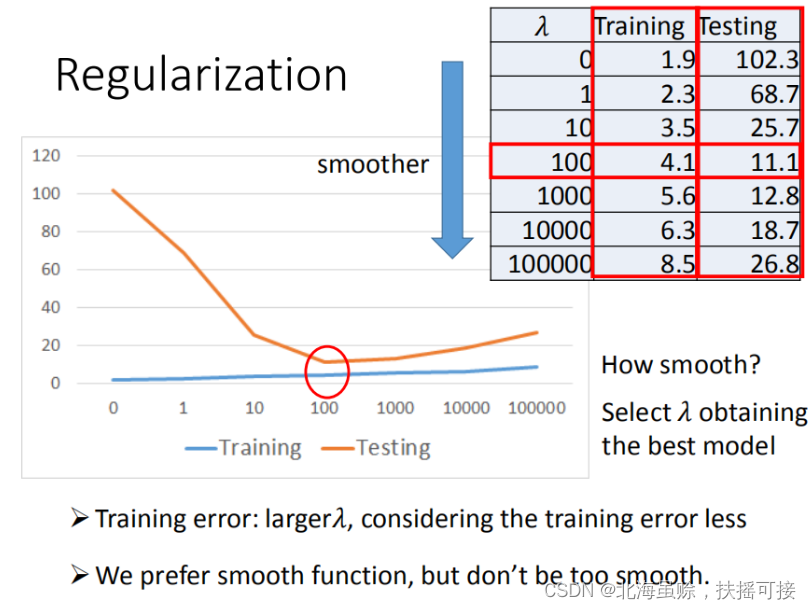
- w 越小,表示 function较平滑的, function输出值与输入值相差不大。
- 在很多应用场景中,并不是 w越小模型越平滑越好,但是经验值告诉我们 w越小大部分情况下都是好的。
- b 的值接近于0,对曲线平滑是没有影响
5、总结
Pokemon:原始的CP值极大程度的决定了进化后的CP值,但可能还有其他的一些因素。
Gradient descent:梯度下降的做法;后面会讲到它的理论依据和要点。
Overfitting和Regularization:过拟合和正则化,主要介绍了表象;后面会讲到更多这方面的理论
解决过拟合方法有很多,除了正则化,还有earlystopping等,具体我也有点忘了。