前言
因为最近看论文发现同一个模型用了不同的注意力机制计算方法,因此懵了好久,原来注意力机制也是多种多样的,为了以后方便看懂人家的注意力机制,还是要总结总结。
注意力机制
注意力机制的计算思路非常简单,只有两步:
- 在输入信息上计算注意力分布
- 根据注意力分布计算输入信息的加权平均
注意力分布的计算简单理解就是算出注意力权重α
得出的权重可以画图可视化注意力关注的点在哪
有了权重即可得出加权求和后得到的特征了
软注意力机制
采取“软性”选择机制,不是从存储的多个信息中只挑出一条信息来,而是雨露均沾,从所有的信息中都抽取一些,只不过最相关的信息抽取得就多一些。
软注意力的注意力分布:
在给定输入信息X和查询向量q下,选择第i个信息的概率,
αi=p(z=i | X, q)
= softmax(s(xi, q))
其中,αi称为注意力分布,s(xi, q)称为注意力打分函数。
注意力打分函数有以下几种形式:
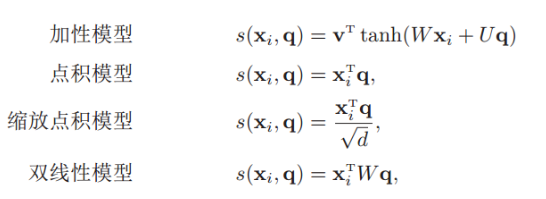
其中W、U和v是可学习的网络参数,d是输入信息的维度。xi为输入的信息,q为输入的查询向量。
加权平均:
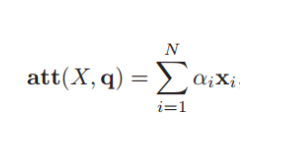
其中X=[x1, x2, …, xN],q为查询向量。
首先X与q计算出注意力分布αi
然后X再与αi加权求和得出注意力机制计算后的结果
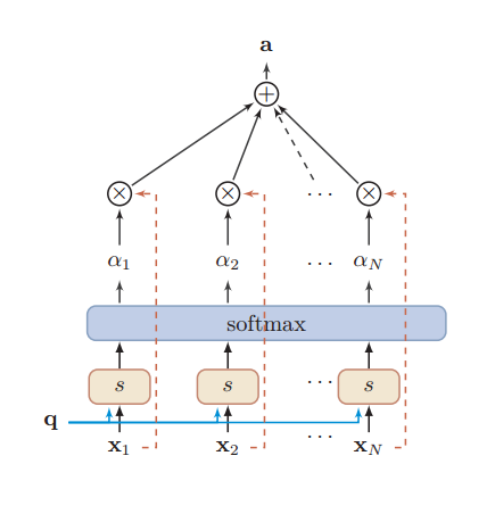
值得注意的是,这里X=[x1, x2, …, xN]用了两次,第一次先与q计算出αi,第二次X与αi计算出注意力机制计算后的结果。
由于X用了两次,不易让人一目了然,我们可以对其进行一般化的处理,引入键值对注意力模式。
用键值对(key-value pair)来表示输入信息,那么N个输入信息就可以表示为(K, V)= [(k1,v1),(k2,v2),…,(kN,vN)],其中“键”(k)用来计算注意分布σi,“值”(v)用来计算聚合信息。
那么软注意力机制的公式可以重写如下:
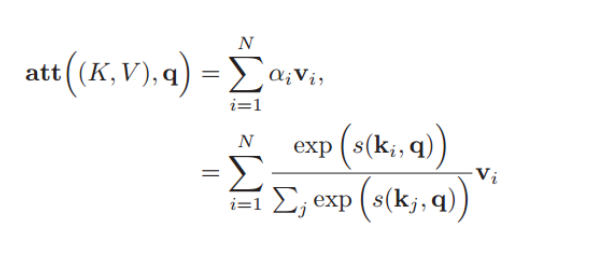
其中(K,V)=([k1,k2…kN],[v1,v2…vN])
K与查询向量q通过注意力打分函数s()对每个v计算出对应的α值,然后Σαivi即可。
这样一来,使得注意力机制更加一般化了。
可以理解为,从对应的ki与q的关系中,能够抽取出多少vi的特征,其中ki和vi并不一定要相等。
那么就可以将注意力机制看做是一种软寻址操作:把输入信息X看做是存储器中存储的内容,元素由地址Key(键)和值Value组成,当前有个Key=Query的查询,目标是取出存储器中对应的Value值,即Attention值。而在软寻址中,并非需要硬性满足Key=Query的条件来取出存储信息,而是通过计算Query与存储器内元素的地址Key的相似度来决定,从对应的元素Value中取出多少内容。每个地址Key对应的Value值都会被抽取内容出来,然后求和,这就相当于由Query与Key的相似性来计算每个Value值的权重,然后对Value值进行加权求和。加权求和得到最终的Value值,也就是Attention值。
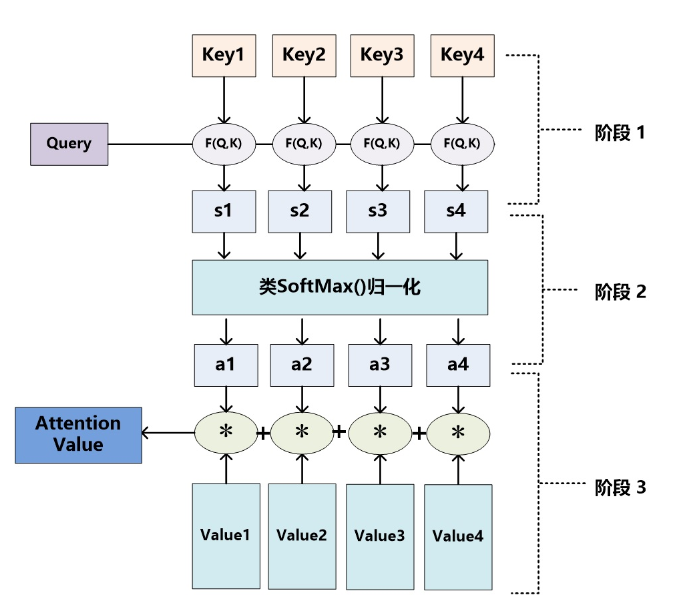
看这副图应该会更好理解。
Transformer中使用的是自注意力机制(self-attention),那么什么是自注意力机制呢?
在上面软注意力机制中提到了键值对注意力模式,那么需要计算注意力需要Q(查询向量)、K(键向量)、V(值向量)三个输入。
当Q=K=V的时候,注意力机制就被称为自注意力机制了。
代码实现
下面将代码实现一下上面不同注意力打分函数的注意力机制,为了方便,全部采取自注意力机制的形式,即Q=K=V。
代码如下:
加性模型
import torch
import torch.nn as nn
import math
import torch.nn.functional as F
# 加性模型
class attention1(nn.Module):
def __init__(self, q_size, k_size, v_size, seq_len):
# q、k、v的维度,seq_len每句话中词的数量
super(attention1, self).__init__()
self.linear_v = nn.Linear(v_size, seq_len)
self.linear_W = nn.Linear(k_size, k_size)
self.linear_U = nn.Linear(q_size, q_size)
self.tanh = nn.Tanh()
def forward(self, query, key, value, dropout=None):
key = self.linear_W(key)
query = self.linear_U(query)
k_q = self.tanh(query + key)
alpha = self.linear_v(k_q)
alpha = F.softmax(alpha, dim=-1)
out = torch.bmm(alpha, value)
return out, alpha
attention_1 = attention1(100, 100, 100, 10)
q = k = v = torch.randn((8,10,100)) # 可以理解为有8句话,每句话有10个词,每个词用100维的向量来表示
out, attn = attention_1(q, k, v)
print(out.shape)
print(attn.shape)
点积模型:
import torch
import torch.nn as nn
import math
import torch.nn.functional as F
# 点积模型
class attention2(nn.Module):
def __init__(self):
super(attention2, self).__init__()
def forward(self, query, key, value, dropout=None):
alpha = torch.bmm(query, key.transpose(-1, -2))
alpha = F.softmax(alpha, dim=-1)
out = torch.bmm(alpha, value)
return out, alpha
attention_2 = attention2()
q = k = v = torch.randn((8,10,100))
out, attn = attention_2(q, k, v)
print(out.shape)
print(attn.shape)
缩放点积模型:
transformer用的就是这种注意力模型,不过是多头,下面会讲到
import torch
import torch.nn as nn
import math
import torch.nn.functional as F
# 缩放点积模型
class attention3(nn.Module):
def __init__(self):
# q、k、v的维度,seq_len每句话中词的数量
super(attention3, self).__init__()
def forward(self, query, key, value, dropout=None):
d = k.size(-1)
alpha = torch.bmm(query, key.transpose(-1, -2)) / math.sqrt(d)
alpha = F.softmax(alpha, dim=-1)
out = torch.bmm(alpha, value)
return out, alpha
attention_3 = attention3()
q = k = v = torch.randn((8,10,100))
out, attn = attention_3(q, k, v)
print(out.shape)
print(attn.shape)
双线性模型:
import torch
import torch.nn as nn
import math
import torch.nn.functional as F
# 双线性模型
class attention4(nn.Module):
def __init__(self, x_size):
# seq_len每句话中词的数量
super(attention4, self).__init__()
self.linear_W = nn.Linear(x_size, x_size)
def forward(self, query, key, value, dropout=None):
alpha = torch.bmm(query, self.linear_W(key).transpose(-1, -2))
alpha = F.softmax(alpha, dim=-1)
out = torch.bmm(alpha, value)
return out, alpha
attention_4 = attention4(100)
q = k = v = torch.randn((8,10,100))
out, attn = attention_4(q, k, v)
print(out.shape)
print(attn.shape)
一般都用点积模型吧。
硬注意力机制
软性注意力机制可以理解为表示的是所有输入向量在注意力分布下的期望,而硬性注意力关注某一个输入向量。
硬性注意力有两种实现方式 :
- 选取最高概率的一个输入向量

- 通过在注意力分布式上随机采样的方式实现(类似掷骰子)
缺点:最终的损失函数与注意力分布之间的函数关系不可导,不能反向传播来训练,需要使用强化学习训练。
不过我到现在还没见过硬注意力机制的代码,也没遇到过要使用的情况,一般都是软注意力机制居多,因此就当了解了解吧。
多头注意力机制
由于单套注意力关注的特征可能有局限性,那么可以多加几套注意力机制来聚焦不同的方面,这就是多头注意力机制,简单来说有几头注意力机制就有几套不同的Q、K、V。
代码实现思路是参考transformer的多头注意力机制实现的,多头可以通过一次矩阵乘法完成,只需要线性变换层即可,也能够使得模型训练的参数变多,使得注意力机制更有效,但是注意力机制并不会记录时序信息,因此在NLP实际使用中还会加入位置编码,详细可以参考transformer的一些理解以及逐层架构剖析与pytorch代码实现
代码实现
import torch
import torch.nn as nn
import math
import torch.nn.functional as F
# 缩放点积模型
class attention3(nn.Module):
def __init__(self):
super(attention3, self).__init__()
def forward(self, query, key, value, dropout=None):
d = key.size(-1)
alpha = torch.matmul(query, key.transpose(-1, -2)) / math.sqrt(d)
alpha = F.softmax(alpha, dim=-1)
out = torch.matmul(alpha, value)
return out, alpha
class MultiheadAttention(nn.Module):
def __init__(self, head, embedding_size, dropout=0.1):
super(MultiheadAttention, self).__init__()
assert embedding_size % head == 0 # 得整分
self.head = head
self.W_K = nn.Linear(embedding_size, embedding_size)
self.W_Q = nn.Linear(embedding_size, embedding_size)
self.W_V = nn.Linear(embedding_size, embedding_size)
self.fc = nn.Linear(embedding_size, embedding_size)
self.dropout = nn.Dropout(dropout)
self.d_k = embedding_size // head
self.attention = attention3()
def forward(self, query, key, value):
batch_size = query.size(0)
# 转换成多头,一次矩阵乘法即可完成
query = self.W_Q(query).view(batch_size, self.head, -1, self.d_k)
key = self.W_K(key).view(batch_size, self.head, -1, self.d_k)
value = self.W_V(value).view(batch_size, self.head, -1, self.d_k)
out, alpha = self.attention(query, key, value, self.dropout)
out = out.view(batch_size, -1, self.d_k * self.head)
out = self.fc(out)
return out, alpha
m = MultiheadAttention(4, 20)
c = torch.randn((4,5,20))
out, alpha = m(c,c,c)
print(out.shape)
print(alpha.shape)
query = self.W_Q(query).view(batch_size, self.head, -1, self.d_k)
query = self.W_Q(query).view(batch_size, -1,self.head, self.d_k).transpose(1, 2)
不懂就问,这两种写法有什么区别吗,看到好多代码都是下面这种写法…
参考
https://www.bilibili.com/video/BV1DK411M73n?p=9&vd_source=f57738ab6bbbbd5fe07aae2e1fa1280f