whole CNN

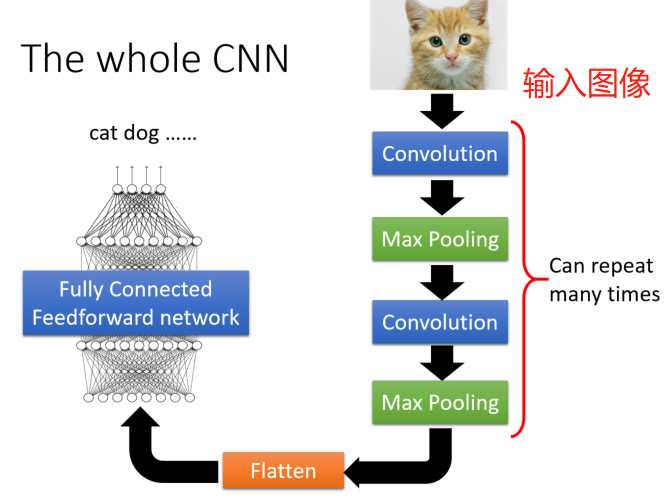
在这里插入图片描述
根据需要分类图像的特点分析，确定需要多少卷积层和池化层。
convolution的特性：

池化层的特性：

convolution

operation

假设有66图像且像素值如下：

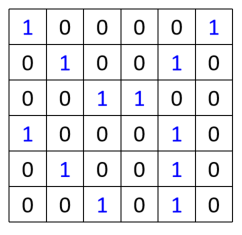
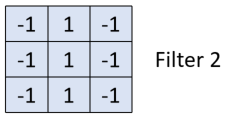
假设有一组filter如下，表现为一个矩阵，其中的每一个数值是网络中的参数，需要学习出来：

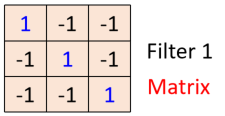
假设这里是33的矩阵，即只侦测的pattern的尺寸就是3*3
下一个问题：这里的filter如何和原图进行运算？

将filter放在图像的左上角，如图

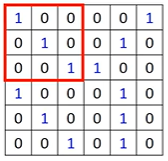
将上图中左上角图像的像素数值和filter的9个数值做内积，得到“3”
挪动filter的位置如下（stride是挪动的距离）

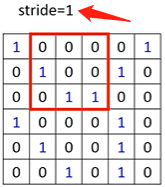
继续内积，得到“-1”
不同的stride得到的数值不同
按照stride=1将滤波器依次平移，下移并作内积
-
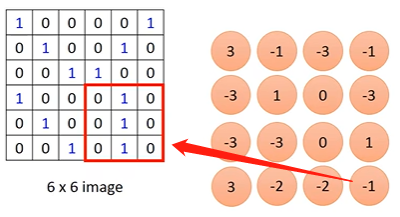
经过这些移动内积运算后，从66的矩阵变成44的矩阵
观察本例中用的的filter，对角线均为“1”，表明这个过程是检测有没有在原图中出现这样连续对角为“1”的情况出现，如果出现，就对应为内积的最大值

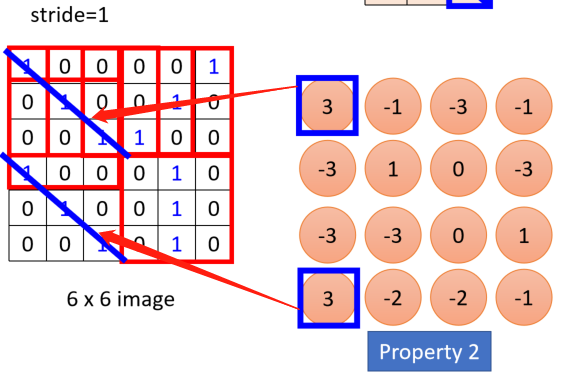
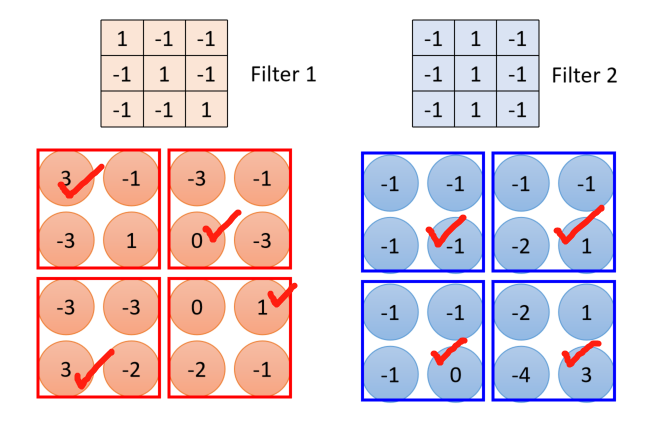
每一个filter表明一个需要检测的特征，因此对每一个filter都做如上的操作

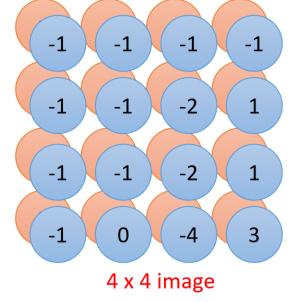
在这里插入图片描述
注意到这里，经过fitler后得到的矩阵比原矩阵维数少2，这是不考虑边缘补0的情况。
如上图所示，可以第二组结论，这些矩阵称为“feature map”。
对彩色图像来说，要在RGB通道上各自做操作，因此此时的filter不在是一个矩阵，而表现为一个立方体
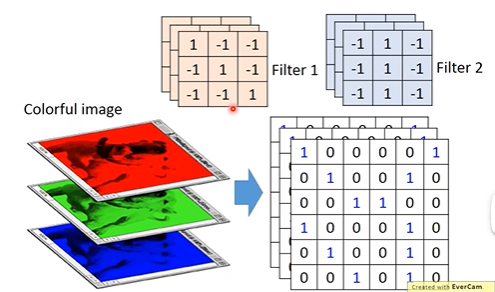
在这里插入图片描述
如图所示，假设每一个色彩通道是66矩阵，则整图表现为366，filter为33*3，即每一个通道都对应一个卷积核，此时filter的27个值和原图中的27个值做内积（注意：并不是每个通道单独算，是合在一起算。

convolution和fully connected的关系

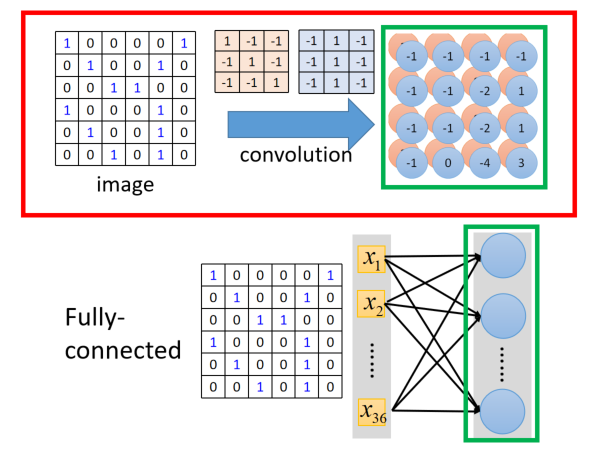
在这里插入图片描述
covolution的操作相当去掉一些元素做加权求和的操作，以filter1为例

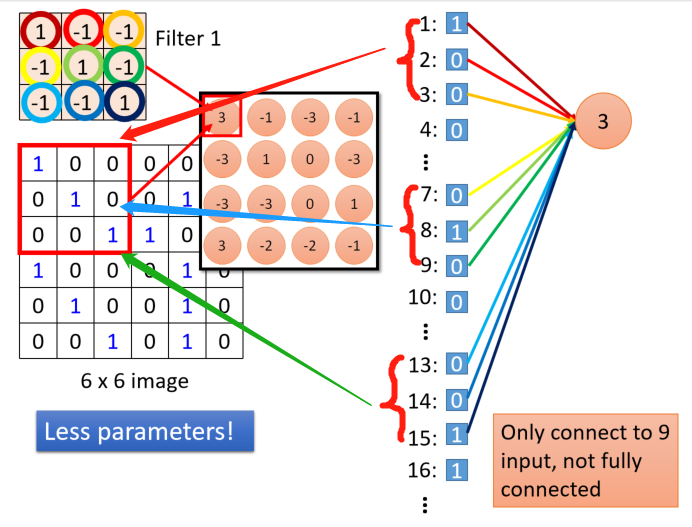
将66图像的所有像素值展开为一个列向量，第一个33的窗口的像素分别对应为“第一行是1,2,3",“第二行是7,8,9”,“第三行是13,14,15”.假设”3“是第一个neuro的结果，就是filter和原图像对应位置内积的结果，那么这个neuro就是只对9个数值进行加权求和，这里的权值就是filter中的数值。
同理：
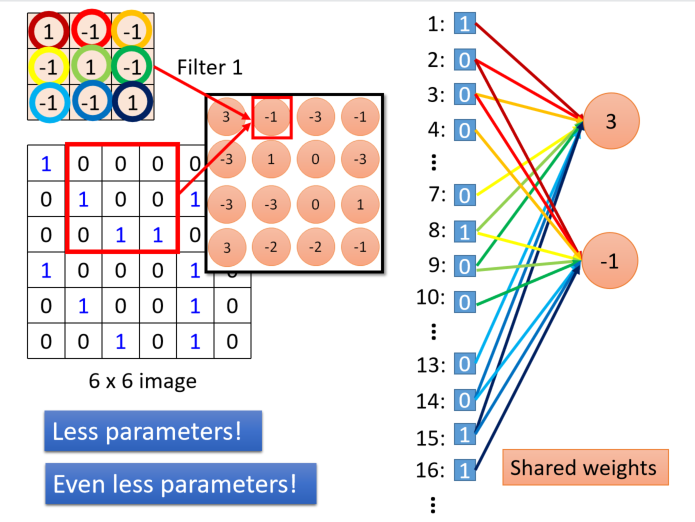
在这里插入图片描述
上图中，不同的颜色代表不同的权值，当移动到第二个位置时，显然对于第一个neuro用到的第一个元素”1“的权值与第二个neuro用到的第二个元素”0“的权值时一样的，就是共享weight。

Max Pooling

对上一步得到的feature map进一步减少元素值，例如，4个为一组，将其中最大的数值保留
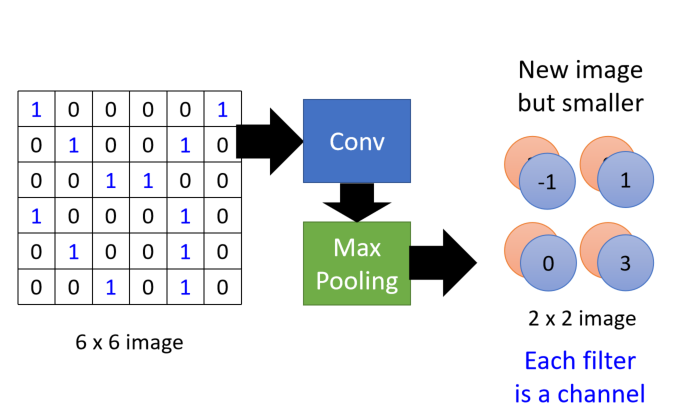
在这里插入图片描述

其深度是指代用了几个filter，如上图的两个颜色就是用2个filter原酸后的结果。这样得到的新的矩阵立方体可以继续在进行convolution–max pooling进一步降低元素个数。

Flatten

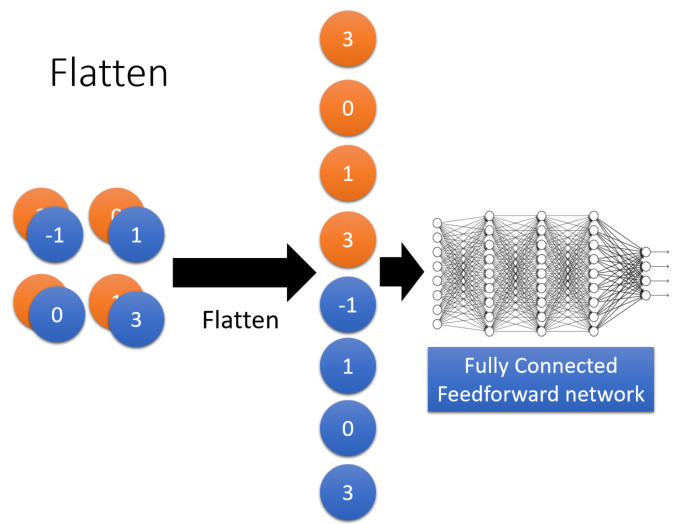
在这里插入图片描述

what does CNN learn

在第二次convolution–pooling时用到的filter的元素并不是像素。
假设：第k个filter的输出时11*11矩阵，如图所示：
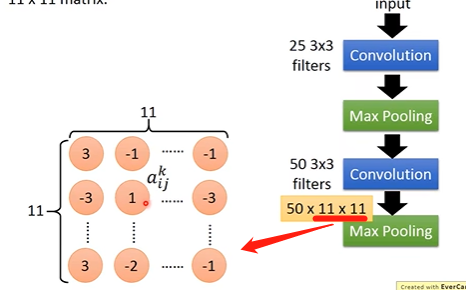
在这里插入图片描述
令该矩阵中某个元素为 $a_{ij}^k$ ,上标k表示第k个filter
定义一个新的参数称为“degree”，表示第k个filter的激活程度，

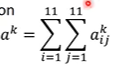
问题转换为找到一个合适的input x，使得这里的 $a^k$ 是最大的，可以采用gradient ascent的方法
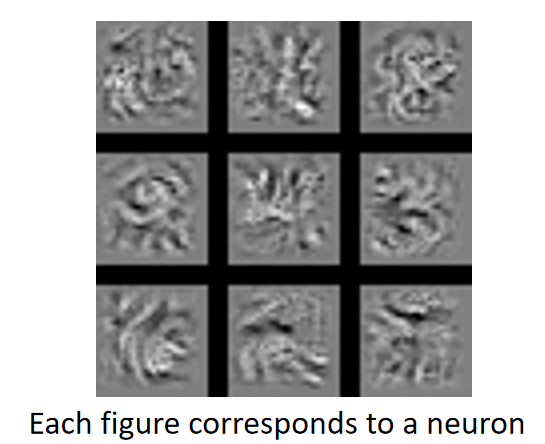
这一步相当于是确定filter的作用，即探测有某个区域。如图为能够使得12个filter最大的图像
在这里插入图片描述
每一个图像就表征了这个filter想要探测出的图形。
考虑如图中的fully connected的工作，假设每一个neuron的输出为 $a^j$

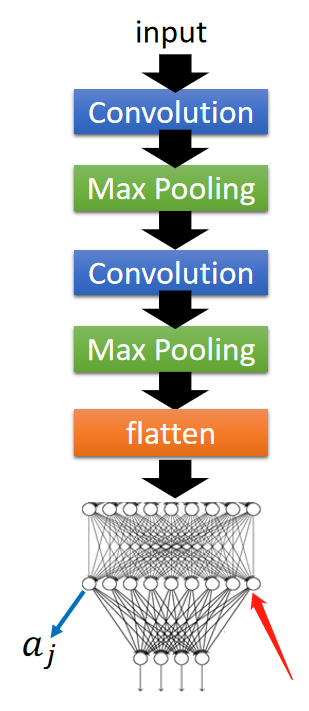
同样的思路，找一张输入x，使得这里的 $a^j$ 最大，如图示例

以此类推，对输出y，同样需要找出一个输入使得output最大
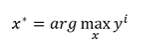
在这里插入图片描述
但是这种方式找出来的图并不是我们想要的很明显的pattern，因此变化思路
不是直接对y找使其最大的输入，而是增加一个所有像素值的sum。