#基于新闻文本、#GCN、#半监督 、#WMD算法(with KNN)
一、文章动机
- 使用半监督学习方法的好处:标记数据将训练过程引导到正确的方向,未标记的数据用于增强模型泛化和性能。在时间,成本,人力和注释不一致方面进行优化。
- 在分类任务中,WMD算法与K-nearest neighbor(K最邻近法)相结合具有非常良好的性能。
- GCN集合了卷积优势和图的数据结构化功能。
【WMD(Word Mover’s Distance)算法】
-
WMD算法是2015年提出,基于word2vec基础上通过计算文本间词的距离来衡量文本相似度的算法。
-
WMD度量值适用于根据语义上接近但在语法上不同的单词之间的对齐方式计算两个文本文档之间的距离。基本上测量两个文本文档之间的差异,作为一个文档的词向量到达另一个文档的词向量所需的最小距离。
-
算法思路:把文本以BOW的方式录入,使用word2vec的词向量矩阵,获得录入文本的每个词的词向量。在衡量两个文本的相似度的时候,计算两个文本的词向量的距离。
对于每个文本中的词出现的次数进行归一化处理,对于文章中第i 个词出现的次数有: d i = c i ∑ j = 1 n c j d_i=\frac{c_i}{\sum_{j=1}^{n}c_j} di?=∑j=1n?cj?ci??,使用 c ( i , j ) = ∣ ∣ x i ? x j ∣ ∣ 2 c(i,j)=||x_i-x_j ||_2 c(i,j)=∣∣xi??xj?∣∣2? 表示两个词间的欧氏距离。
WMD对于两个词之间的距离计算公式如下所示:
∑ j = 1 n T i j = d i \sum_{j=1}^{n} T_{ij}=d_i ∑j=1n?Tij?=di?
∑ i = 1 n T i j = d j ’ \sum_{i=1}^{n} T_{ij}=d_j^’ ∑i=1n?Tij?=dj’?
每对词 i i i 和 j j j 间的距离设定权重参数 T ( i , j ) T_(i,j) T(?i,j) ,使得文章D的第i个词对应到 D ’ D’ D’文章中所有的词的权重值和等于 d i d_i di?。同理,文档 D ’ D’ D’的第 j j j个词的权重值的和等于 d j ’ d_j^’ dj’?。为了达到 ∑ i , j = 1 n T i , j \sum_{i,j=1}^nT_{i,j} ∑i,j=1n?Ti,j? 最优,使用时间动态规划算法(DP)。
二、模型架构
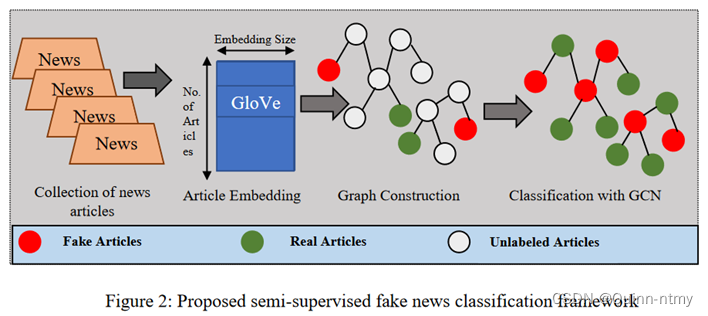
大体包括三个基本组件:
(1)利用GloVe从数据集中的新闻文章中收集词嵌入:求出每个单词的GloVe向量,并且求均值得到文章嵌入;
(2)使用Word Mover’s Distance(WMD)算法构建新闻之间的相似度图(同质图);
(3)使用GCN在半监督中得到新闻文本嵌入,对新闻文章进行二元分类。
三、实验详细步骤
1、数据预处理阶段:删除未使用的列、空和缺失数据,删除停用词,tokenize化文章,对每个单词进行词形还原(lemmatization),转换标签名称等。
2、将输入样本拆分为80%训练集,10%验证集,10%测试集。
3、创建三种类型节点:真实、虚假、未标记。
4、使用GloVe嵌入将文章转换为矢量,Embedding Dim=300 。
5、将每篇文章都表示为GloVe嵌入(步骤4生成)所包含的单词向量的平均值。
6、嵌入的结果用于在数据集中的文章之间构造相似图,使用具有K-nearest neighbour的WMD构建相似性图,K=3和K=5。(每个节点代表一篇文章,大多数相似的节点都通过图形中的边缘连接)
7、训练4层的GCN,120个epoch,dropout=0.5,lr=0.01。
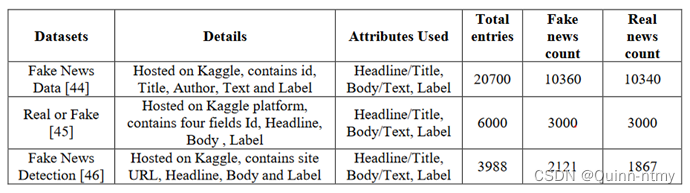
四、数据集