前言
在卷积神经网络示例中,我们注意到,在每个MaxPooling2D层之后,特征图的尺寸都会减半。例如:在第一个MaxPooling2D层之前,特征图的尺寸是26 * 26,但最大池化运算将其减半为13 * 13。这就是最大池化的作用:对特征图进行下采样,与步进卷积类似。
提示:以下是本篇文章正文内容,下面案例可供参考
一、最大池化
最大池化是从输入特征图中提取窗口,并输出每个通道的最大值。它的概念与卷积类似,但是最大池化使用的硬编码的max张量运算对局部图块进行变换, 而不是使用学到的线性变换(卷积核)。最大池化与卷积的最大不同之处在于,最大池化通常使用2 * 2的窗口和步幅2,其目的是将特征图下采样2倍。与此相对的是,卷积通常使用3 * 3窗口和步幅1。
二、为什么要对特征图进行下采样
我们为什么要用这种方式对特征图下采样呢?为什么不删除最大池化层,一直保留较大的特征图?我们来这么做试一下。这时模型的卷积基如下所示:
model_no_max_pool = models.Sequential()
model_no_max_pool.add(layers.Conv2D(32,(3,3),activation='relu',input_shape=(28,28,1)))
model_no_max_pool.add(layers.Conv2D(64,(3,3),activation='relu',input_shape=(28,28,1)))
model_no_max_pool.add(layers.Conv2D(64,(3,3),activation='relu',input_shape=(28,28,1)))
print(model_no_max_pool.summary())
该模型的架构如下:
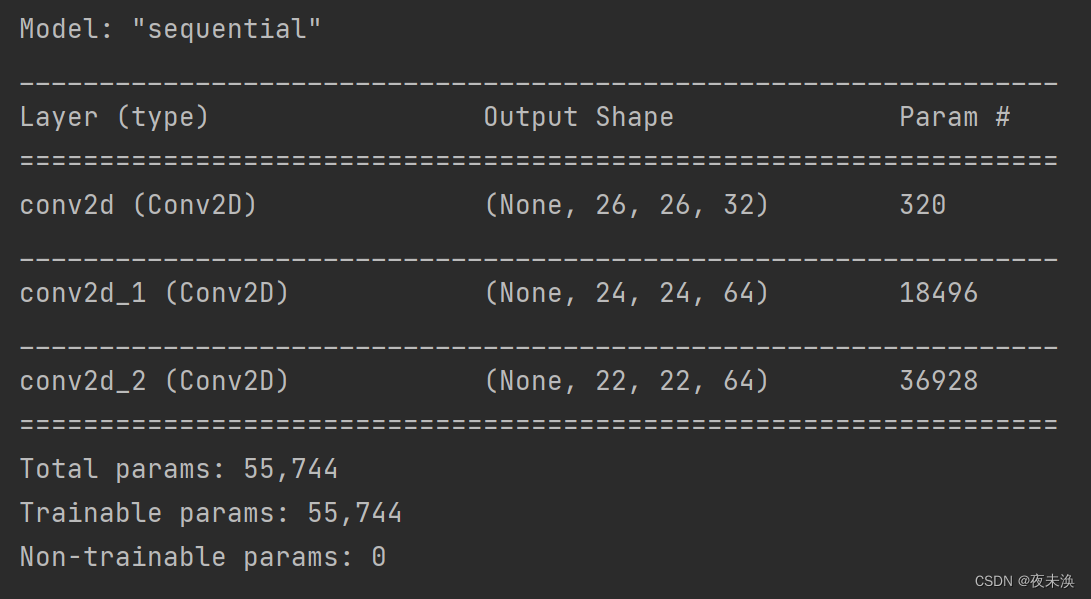
这种架构的问题如下:
- 这种架构不利于特征的空间层次结构。第三层的3 * 3窗口中只包含初始输入的7 * 7窗口中所包含的信息。卷积神经网络学到的高级模式相对于初始输入来说仍然很小,这可能不足以学会对数字进行分类(你可以试试仅通过7像素*7像素的窗口观察图像来识别其中的数字)。我们需要让最后一个卷积层的特征包含输入的整体信息。
- 最后一层的特征图对每个样本共有22 * 22 * 64=30976个元素。这太多了,如果你将其展平并在上面添加一个大小为512的Dense层,那一层将会有1580万个参数。这对于这样一个小模型来说太多了,会导致严重的过拟合。
简而言之,使用下采样的原因,一是减少需要处理的特征图的元素个数,二是通过让连续卷积层的观察窗口越来越大(即窗口覆盖原始输入的比例越来越大),从而引入空间过滤器的层级结构。
注意,最大池化不是实现这种下采样的唯一方法。你已经知道,还可以在前一个卷积层中使用步幅来实现。此外,你还可以使用平均池化来代替最大池化,其方法是将每个局部输入图块变换为取该图块各通道的平均值,而不是最大值。但最大池化的效果往往比这些替代方法更好。简而言之,原因在于特征中往往编码了某种模式或概念在特种图的不同位置是否存在(因此得名特征图),而观察不同特征的最大值而不是平均值能够给出更多的信息。因此,最合理的子采样策略是首先生成密集的特征图(通过无步进的卷积),然后观察特征每个小图块上的最大激活,而不是查看输入的稀疏窗口(通过步进卷积)或对输入图块取平均,因为后两种方法可能导致错过或淡化特征是否存在的信息。