写在前面
是在Monopair的启发下完成的工作。论文提到是提出的结构可以作为一个独立的插件提升3D模型检测效果,因此有兴趣读一下
主要工作一览
如图1所示,核心思想是建立所有目标对象之间的联系,并全局优化它们的3D位置。此外,还通过逆投影映射将BEV与图像视图相关联,并将2D检测结果用于指导BEV中的3D定位。为了达到这一目标,提出了单应损失,将2D和3D信息结合起来,并全局平衡相互之间的关系,以获得更准确的3D方框。通过这样做,提出的损失函数能够有效地编码2D和3D空间中必要的几何信息,并且网络将被强制显式地捕捉对象之间的全局几何关系,这被证明是有助于3D检测的。由于可区分和可解释,损失函数可以插入任何成熟的单目3D探测器。实践中,以IMV oxelNet和MonoFlex为例,结合训练阶段的新的单应性损失,在Kitti 3D检测基准(2021年11月)上实验表明方法的性能远远超过最新技术。主要贡献可概括如下:

1.提出了一种新的损失函数,称为单应损失(homography loss,为方便写作下文皆称Hloss),利用图像视图和鸟眼视图之间的单应关系,利用场景中所有对象的几何关系,全局地约束它们的相互位置。同时,2D和3D空间的几何一致性将得到很好的保持。这是第一个在单目3D目标检测中充分利用全局几何约束的工作。
2.基于单应损失的单目3D探测器达到了Kitti 3D检测基准的最新性能,并超过了所有其他单目3D探测器的结果,表明了提出的损失函数的优越性。
3.将该损失函数应用于几种流行的单目3D探测器。在不增加任何额外推理代价的情况下,训练更加稳定,更容易收敛,实现了更高的精度和性能。证明其是一个即插即用的模块,可以适用于任何单目3D探测器。
方法论
Hloss提出的意义与依据论述
基于这样的两个事实:
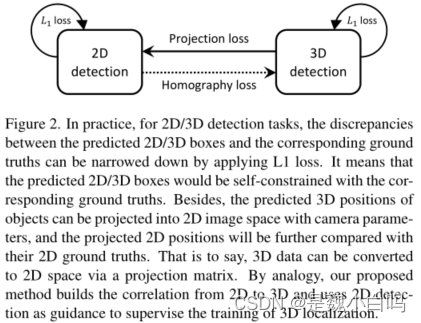
1.任一2D/3D检测任务,两者都可通过应用L1损失来缩小预测的2D/3Dbox和对应的真值之间的差异。这意味着预测的2D/3Dboix将受到相应GT的自我约束。
2.一般地,3D数据可以通过投影损失(Projection loss)转换为2D空间的数据。
因此可以类推出结论:可以建立一个2D到3D空间的损失,以2D的目标检测知道3D定位的监督训练。
从数学模型角度推理引出Hloss的提出设计意义和依据(图2)。
论文也给出了从拓扑学角度的推论
 ?
?
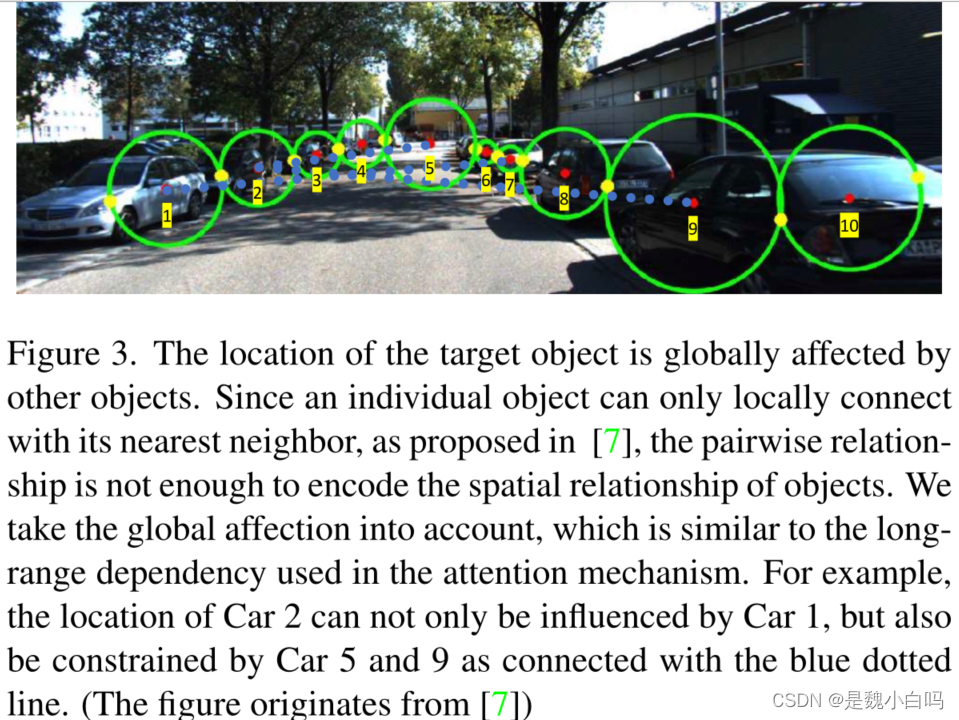
论文提出,之前的工作只考虑了相邻的连接关系,这不足以编码多个目标对象之间的空间关系。本文考虑了提到的这种全局关系,并指出这类似于注意力机制中的远程依赖。例如,2号车的位置不仅会受到1号车的影响,还会受到5号车和9号车的约束,因为它们与蓝色虚线相连。
Hloss
首先是二维点到三维点的转换关系:
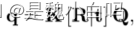
其中,q为像素点,Q为三维位置点,K是内参矩阵,Rt为外参矩阵?。
并通过H矩阵换算:
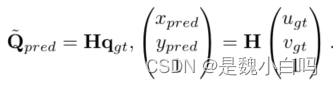
其中,H表示单应矩阵,H通过两个视图之间的映射来存储所有目标对象的相互关系。本文使用奇异值分解(SVD)来计算单应矩阵H。
最后转化为loss函数形式:
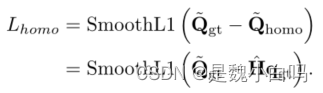
可以看到,主要是借助SmoothL1来实现计算的可微分的形式构建。
真正使用的时候自然是以多损失组合的形式出现。
整个过程倒不是很难理解,重点是这个点子的形成过程,也就是逻辑的推导过程,很值得学习。
试验
这里只粘贴了表1,其他试验数据可看论文
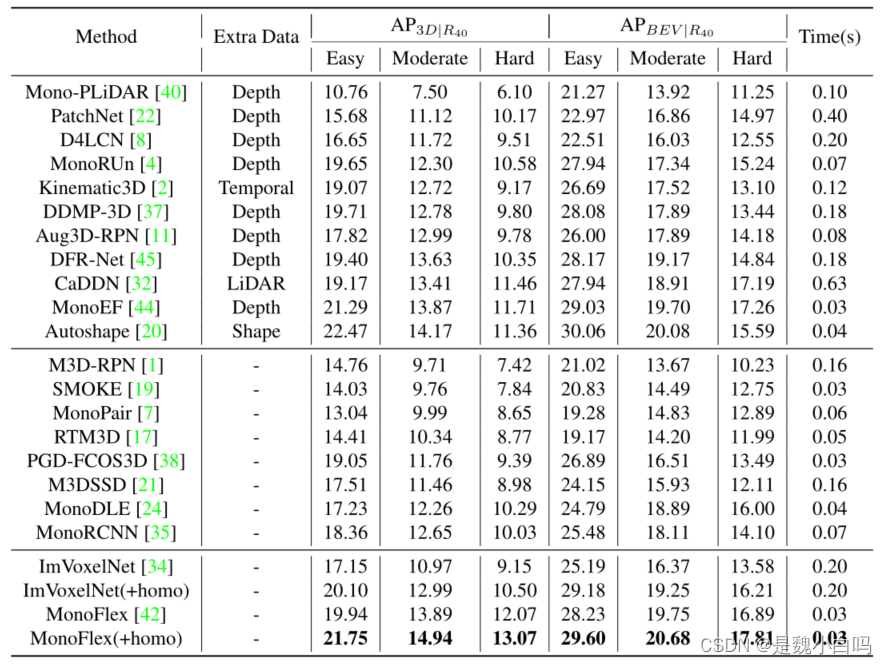
可以的看到全面实现了单目3D检测的SOTA