声明:本文为学习笔记,侵权删
一、相关系数r
r类似于直线斜率k,r>0,则表示正相关,r<0,则表示负相关。
|r|表示相关程度:
|r|=0? ? ? ? ? ? ? ? ? ? ? ? 非线性相关
|r| ∈?(0,0.3)? ? ? ? ? ? 弱线性相关
|r| ∈ [0.3,0.8)? ? ? ? ?中度线性相关
|r| [0.8,1]? ? ? ? ? ? ? ? ?强线性相关
要注意的是:相关性并不代表因果关系。
比如这幅图,难道人造黄油消费量下降导致了离婚率下降???
因此,通常情况下,在进行回归分析之前,需要主观判断两个变量是否具有因果关系。存在因果关系接下来的回归分析才有意义。
回归分析分为线性回归和非线性回归,线性回归又分为一元线性(一个自变量和一个因变量)和多元线性回归(多个自变量和一个因变量)。
二、一元线性回归
线性回归分析通常分为五步:
S1:绘制散点图,确定相关系数
S2:确定自变量和因变量
S3:建立回归模型(初始化模型,训练模型,查看系数和截距)【构建回归模型,我们采用最小二乘法。】
S4:检验回归模型
S5:使用模型预测
所谓建立回归模型,在一元线性回归中,就是在二维平面上找到一条最能够反映出数据关系的直线。但无论如何,除非r=±1,否则即使这条直线最能够描述数据关系,并不是所有的数据点都会落在这条直线上。若最佳直线是Y=kx+b,对于每一个数据点,X和Y的实际的数学关系可能是Y=kx+b+ε。其中ε为误差。对于一条最佳直线,ε应当是最小的。
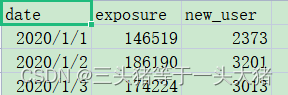
用下面这个数据集为例,描述了广告的曝光度和用户增长的数据。
 ?
?
首先,计算出保管度和用户增长数据之间的相关系数:
import pandas as pd
data = pd.read_csv(r"D:\Python Code\dataMining\ad_exposure.csv")
r = data["exposure"].corr(data["new_user"])
print(r) #r=0.9923775641391593很显然,r=0.99,强线性相关。接着画出对应的exposure和new_user的散点图,可以看出确实两者的正相关的关系是很清晰的:
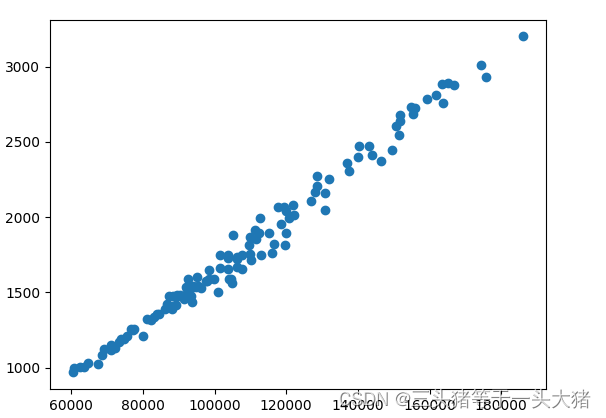
?
接下来,确定自变量和因变量。通过常识,可以推断出,广告曝光度是自变量,用户增长是因变量。
三、一元线性回归模型的构建与应用
即:根据曝光度预测新用户的数量
from turtle import color
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
data = pd.read_csv(r"D:\Python Code\dataMining\ad_exposure.csv")
r = data["exposure"].corr(data["new_user"])
print(r) #r=0.9923775641391593
plt.scatter(data["exposure"],data["new_user"])
plt.xlabel("曝光度")
plt.ylabel("新增用户")
#建立模型并训练模型
x=data[["exposure"]]#注意:自变量一定是二维列表
y=data["new_user"]#因变量可以是一维也可以是二维列表
#初始化线性回归模型
lr = LinearRegression()
#训练模型
lr.fit(x,y)
print(lr.coef_[0])#直线y=kx+b的斜率k 输出:0.018204640095790838
print(lr.intercept_)#直线的y轴截距b 输出:-181.57552715797647
#使用score()函数,计算判定系数。判定系数∈[0,1],越接近1说明模型精度越高
score = lr.score(x,y)
print(score)# 0.9848132298067719 接近1,说明模型精度较高
#使用predict()函数,计算预测值.注意,predict输入的参数也要求是二维列表
pred = lr.predict([[200000],[16000],[43546]])#此处计算了三个预测值
print(pred)#[3459.352492 109.69871437 611.16373045]分别对应根据上面三个曝光度预测得到的新用户数量
#把得到的线性模型画在图上
plt.plot(data["exposure"],lr.coef_*data["exposure"]+lr.intercept_,color="orange")
plt.show()
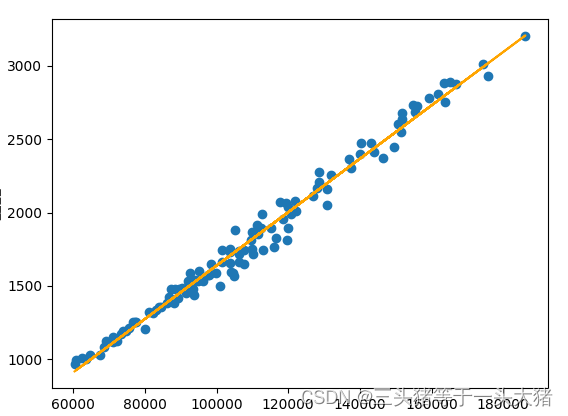
?
四、多元线性回归的应用
多元线性回归与一元线性回归的差别就在于他有多个自变量,同时,多元线性回归也只有一个因变量。分析步骤与一元线性回归类似。
这里使用如下的数据集,同样是关于新用户数量,只不过多了几个自变量:

?先通过散点图,看看数据集中每一个自变量和因变量之间的关系,并计算出两两之间的相关系数:
import pandas as pd
import seaborn as sb
import matplotlib.pyplot as plt
data = pd.read_csv(r"D:\Python Code\dataMining\ad_exposure_multi.csv")
#画出两两之间数据的散点图分布,对角线上的柱状图描述的是那一行/列自身数据的分布情况
sb.pairplot(data)
plt.show()
#计算两两之间的相关系数
data_corr = data.corr()
print(data_corr)
输出:
exposure rank hot search new_user
exposure 1.000000 0.090620 0.516877 0.507091 0.904991
rank 0.090620 1.000000 -0.274103 -0.297074 -0.054877
hot 0.516877 -0.274103 1.000000 0.993623 0.769915
search 0.507091 -0.297074 0.993623 1.000000 0.761797
new_user 0.904991 -0.054877 0.769915 0.761797 1.000000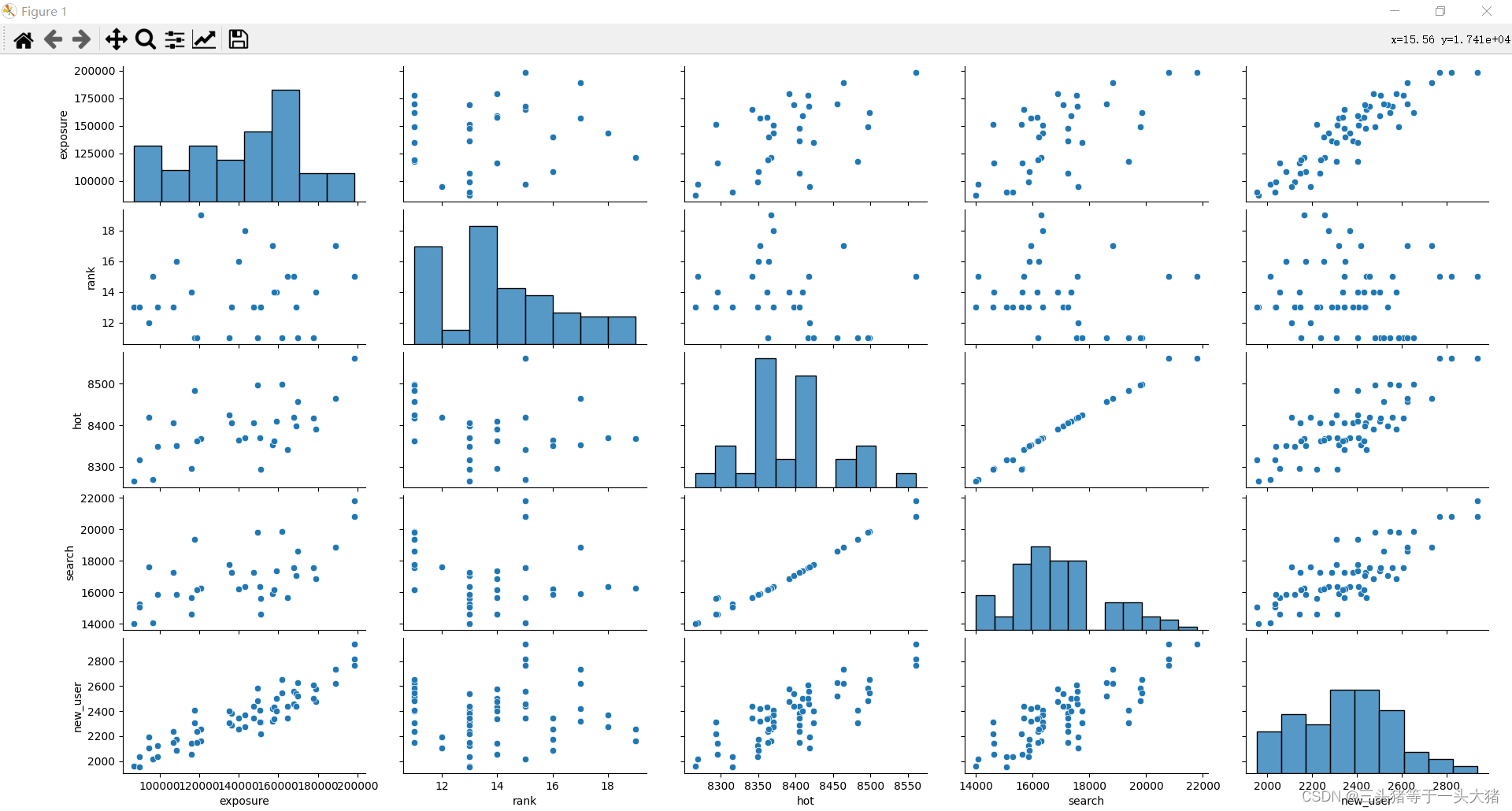
?
如果计算出来的相关系数不够直观,可以绘制热力图:
#绘制关于相关系数的热力图 cmap设置颜色,此处为红蓝
#square:每个单元格是不是正方形
#annot:每个单元格里是否显示数值
sb.heatmap(data_corr, cmap="RdBu",square=True,annot=True)
plt.show()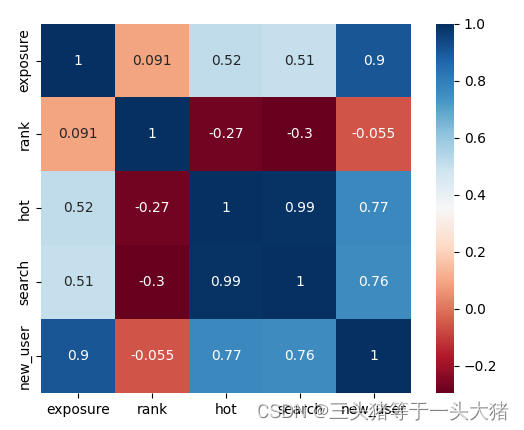
接下来一步:选定自变量和因变量。由于现在存在多个自变量,有些自变量可能关系不大,因此需要筛选出相关性较高的那些自变量最为模型的输入。根据常识,因变量可以确定,为新用户(new_user)。那么自变量呢?通过上面每个变量之间的相关系数画出的散点图或热力图可以看出:曝光度(exposure),热度(hot),搜索量(search)与新用户的变化有较大的关系,而rank没啥关系。所以,自变量选定为曝光度,热度,搜索量。
接下来:建立模型并训练。与一元线性回归(y=kx+b)相似,多元线性回归只不过把一元线性回归得到的直线推广到高维,变成面、体甚至更高维,即
x = data[["exposure","hot","search"]]
y = data["new_user"]
#如果自变量比较多,一个个写比较麻烦,可以用下面几行代替x = data[["exposure","hot","search"]]
#Corr = data_corr["new_user"].drop(index="new_user")
##取相关系数绝对值大于0.6的,0.6是主观设定的
#indexes = Corr[abs(Corr)>0.6].index.values#.values加不加不影响结果,加了values是为了下一行的print输出会清楚一些
#print(indexes)#["exposure","hot","search"]
#x = data[indexes]
lr = LinearRegression()
lr.fit(x,y)
print(lr.coef_) #[0.00485872 1.00583097 0.01321146]
print(lr.intercept_) #-7004.53064849516
#new_user=0.0048*exposure + 1.0058*hot + 0.0132*search - 7004.53
#评估模型
valid = lr.score(x,y)
print(valid) #0.9437117881084567 0.9,挺好的
from sklearn.metrics import r2_score
print(r2_score(y,lr.predict(x))) #0.9437117881084567 另一种评估方法(r2被称为判定系数)
#预测
predict = lr.predict([[23411,53323,23427],[300234,10907,30235]])#测试两组数据
print(predict)#[47052.64627675 5824.26795237]五、多重共线性和过拟合
多重共线性
仔细观察上面的数据,很容易发现:hot和search之间是强线性相关的,hot,search和exposure之间也是中度线性相关的。可是上面设计模型的时候并没有考虑到自变量之间的相关性。事实上,自变量之间的相关性会对模型产生影响。这种情况叫做多重共线性。如果不处理,很容易出现过拟合。
多重共线性的判断有两个方法:相关系数法和方差膨胀系数法(VIF检验)。相关系数法就是上面提到的,通过输出各个自变量之间的相关系数,主观判断是否存在多重共线性。需要注意的是,相关系数高是多重共线性的充分不必要条件。存在多重共线性并不能说明自变量间相关系数一定高。因此,为了结论更加严谨,更多得采用VIF检验。
VIF的值表示一个自变量与其余自变量之间共线的程度。
VIF<10? ? ? ? ? ? ?不存在多重共线性
10≤VIF<100? ? ?较强的多重共线性,视情况而定
VIF≥100? ? ? ? ? ?严重的多重共线性,必须处理
还是用上面的数据做个例子:
from statsmodels.stats.outliers_influence import variance_inflation_factor
data = pd.read_csv(r"D:\Python Code\dataMining\ad_exposure_multi.csv")
x = data[["exposure", "hot", "search"]]
y = data[["new_user"]]
#VIF检验
#x.columns.get_loc(i)表示返回i所在列的列序号数字。如,第1列,返回数字0;第2列,返回数字1,以此类推。
vif = [variance_inflation_factor(x.values, x.columns.get_loc(i)) for i in x.columns]
print(vif)#[32.31907643878631, 136.9115541589221, 176.7628569694301]
#输出代表exposure_VIF=32.31 hot_VIF=136.91 search_VIF=176.76 从上面的输出可以得到:hot和search的VIF都大于100,因此必须处理。上文提到,多重共线性会导致过拟合,因此,可以先通过数据集划分,将原始数据集分为训练集和测试集(一般二八分或者三七分),避免数据集本身带来的过拟合问题(即:数据集划分本就是一种避免过拟合的方法,可以很好得加强模型的泛化性)。
#数据集划分,这里用二八分(0.2的测试集)
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=1)
lr = LinearRegression()
lr.fit(x_train,y_train)
print(lr.score(x_test,y_test))#0.94402942946134 结果说明模型不错接下来,数据集处理完了,我们开始解决多重共线性的问题。
常见的解决方法有:手动移除自变量,逐步回归法,岭回归。
手动移除自变量
顾名思义,手动把不想要的自变量删掉,像这样:
x = x.drop(columns="hot")
vif = [variance_inflation_factor(x.values, x.columns.get_loc(i)) for i in x.columns]
print(vif) #[32.18058990784746, 32.18058990784746]
x = x.drop(columns="search")
vif = [variance_inflation_factor(x.values, x.columns.get_loc(i)) for i in x.columns]
print(vif)#[24.92545466605748, 24.92545466605748]这里分别去掉了hot和search,可以看出,去掉search的时候vif值更小。
那么如何判断存在严重多重共线性的自变量是否对模型有影响呢?通常通过两个方面去评判:模型的score评分和生成模型y=k1x1+...+knxn+b中,相关系数(k1...kn以及b)的变化。
分别尝试去掉hot和search,通过score函数看看对结果有没有什么大的改变。运行后发现,去掉hot, score的得分为0.944809238253474,比没删的时候高了一丢丢,去掉search的时候,score得分为0.9438771873898076,比去掉之前还低了一丢丢。不过这点变化实在太小,基本可以说明:hot和search至少对模型的score的评分没什么影响。
那么再来看看相关系数的变化。
#原始数据集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=1)
lr = LinearRegression()
lr.fit(x_train,y_train)
print(lr.coef_)#[[0.0047 1.09843685 0.01140502]]
print(lr.intercept_)#[-7723.96582017]
#删掉hot
x = x.drop(columns="hot")
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=1)
lr = LinearRegression()
lr.fit(x_train,y_train)
print(lr.coef_)#[[0.00474731 0.05530953]]
print(lr.intercept_)#[741.83652988]
#删掉esearch
x = x.drop(columns="search")
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=1)
lr = LinearRegression()
lr.fit(x_train,y_train)
print(lr.coef_)#[[0.00469407 1.37825535]]
print(lr.intercept_)#[-9877.68111726]通过三次对比发现,原始数据中,y轴截距是-7723,也就是说,exposure,hot,search都为0的时候,新用户的数量是-7723,反倒少人了。而且少的也太多了,是不正常的数据。同样的情况发生在删掉search的时候。而删掉hot的时候,y轴截距为741,也就是时候就算没曝光,没热度,没搜索,依旧会有一定新用户增长,稍微正常一点(毕竟老用户推荐新用户,不需要曝光热度和浏览量)。
这样的情况就说明,原始的模型是失真的。同时,删掉search可能会导致和没删一样的问题:模型失真,因此search对结果的价值比较大,不该被删掉。而hot呢,删掉以后模型变正常了,那就删了吧。
关于岭回归和逐步回归,我参考的是这两篇文章[逐步回归,岭回归],这里就不详述了。不过有一点要说明:逐步回归和岭回归两个方法做出来的结果和上面手动删除系数的方法结论是反的,具体原因我也不晓得,还请大佬教教~