1.软件版本
MATLAB2010b
2.模糊神经网络理论概述
? ? ? ? 由于模糊控制是建立在专家经验的基础之上的,但这有很大的局限性,而人工神经网络可以充分逼近任意复杂的时变非线性系统,采用并行分布处理方法,可学习和自适应不确定系统。利用神经网络可以帮助模糊控制器进行学习,模糊逻辑可以帮助神经网络初始化及加快学习过程。通常神经网络的基本构架如下所示:
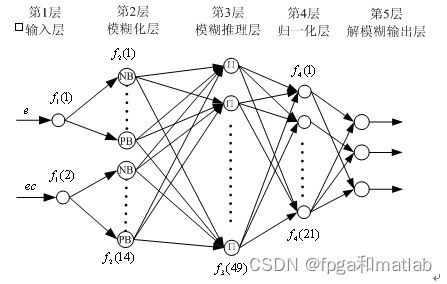
? ? ? 整个神经网络结构为五层,其中第一层为“输入层“,第二层为“模糊化层”,第三层为“模糊推理层”,第四层为“归一化层”,第五层为“解模糊输出层”。?
? ? ? 第一层为输入层,其主要包括两个节点,所以第一层神经网络的输入输出可以用如下的式子表示:
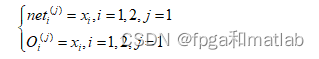
![]()
? ? ? ??第二层为输入变量的语言变量值,通常是模糊集中的n个变量,它的作用是计算各输入分量属于各语言变量值模糊集合的隶属度。用来确定输入在不同的模糊语言值对应的隶属度,以便进行模糊推理,如果隶属函数为高斯函数,那么其表达式为:
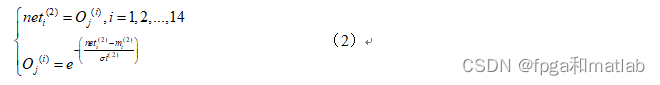
其中变量的具体含义和第一层节点的变量含义相同。
第三层是比较关键的一层,即模糊推理层,这一层的每个节点代表一条模糊规则,其每个节点的输出值表示每条模糊规则的激励强度。该节点的表达式可用如下的式子表示:
?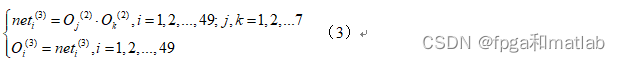
第四层为归一化层,其输出是采用了Madmdani模糊规则,该层的表达式为:?
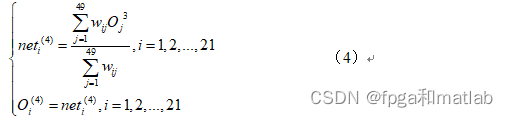
第五层是模糊神经网络的解模糊层,即模糊神经网络的清晰化.?
3.算法的simulink建模
? ? ? ? 为了对比加入FNN控制器后的性能变化,我们同时要对有FNN控制器的模型以及没有FNN控制器的模型进行仿真,仿真结果如下所示:
? ? ? ? 非FNN控制器的结构:
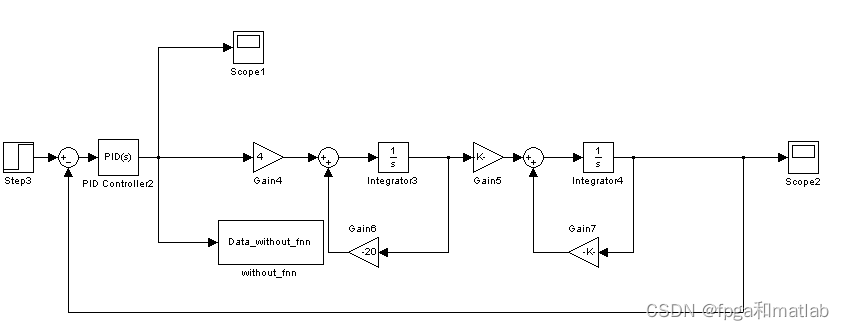
其仿真结果如下所示:
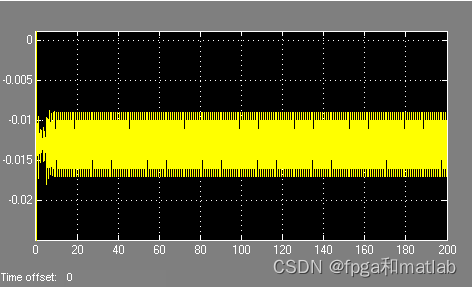
FNN控制器的结构:
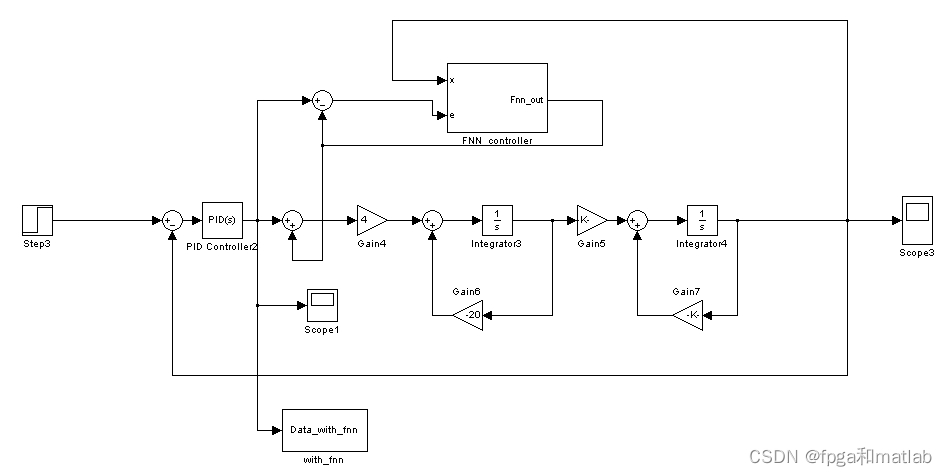
??? 其仿真结果如下所示:
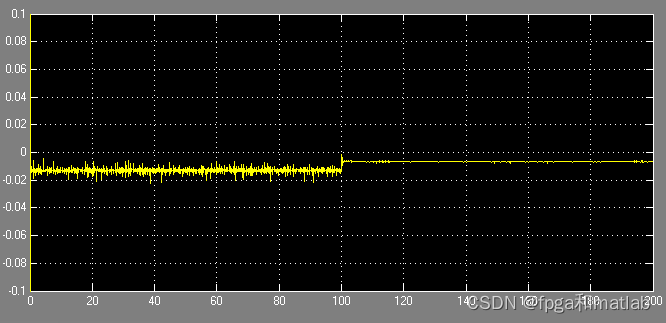
前面的是训练阶段,后面的为实际的输出,为了能够体现最后的性能,我们将两个模型的最后输出进行对比,得到的对比结果所示:
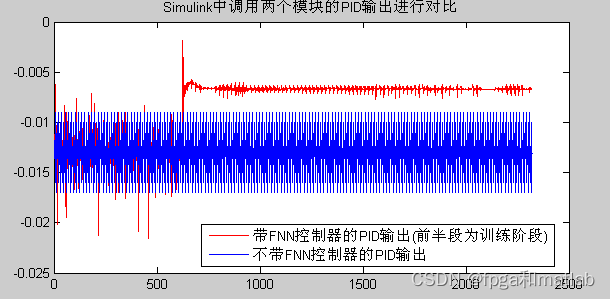
?? 从上面的仿真结果可知,PID的输出值范围降低了很多,性能得到了进一步提升。
调速TS模型,该模型最后的仿真结果如下所示:
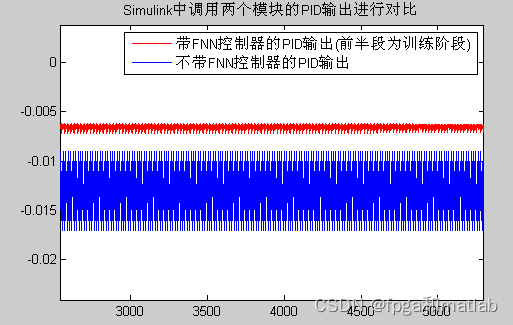
??? 从上面的仿真结果可知,采用FNN控制器后,其PID的输出在一个非常小的范围之内进行晃动,整个系统的性能提高了80%。这说明采用模糊神经网络后的系统具有更高的性能和稳定性。
4.部分程序
Mamdani模糊控制器的S函数
function [out,Xt,str,ts] = Sfunc_fnn_Mamdani(t,Xt,u,flag,Learn_rate,coff,lamda,Number_signal_in,Number_Fuzzy_rules,x0,T_samples)
%输入定义
% t,Xt,u,flag :S函数固定的几个输入脚
% Learn_rate :学习度
% coff :用于神经网络第一层的参数调整
% lamda :神经网络的学习遗忘因子
% Number_signal_in :输入的信号的个数
% Number_Fuzzy_rules :模糊控制规则数
% T_samples :模块采样率
%输入信号的个数
Number_inport = Number_signal_in;
%整个系统的输入x,误差输入e,以及训练指令的数组的长度
ninps = Number_inport+1+1;
NumRules = Number_Fuzzy_rules;
Num_out1 = 3*Number_signal_in*Number_Fuzzy_rules + ((Number_signal_in+1)*NumRules)^2 + (Number_signal_in+1)*NumRules;
Num_out2 = 3*Number_signal_in*Number_Fuzzy_rules + (Number_signal_in+1)*NumRules;
%S函数第一步,参数的初始化
if flag == 0
out = [0,Num_out1+Num_out2,1+Num_out1+Num_out2,ninps,0,1,1];
str = [];
ts = T_samples;
Xt = x0;
%S函数的第二步,状态的计算
elseif flag == 2
%外部模块的输出三个参数变量输入x,误差输入e,以及训练指令的数组的长度
x = u(1:Number_inport);%输入x
e = u(Number_inport+1:Number_inport+1);%误差输入e
learning = u(Number_inport+1+1);%训练指令的数组的长度
%1的时候为正常工作状态
if learning == 1
Feedfor_phase2;
%下面定义在正常的工作状态中,各个网络层的工作
%层1:
In1 = x*ones(1,Number_Fuzzy_rules);
Out1 = 1./(1 + (abs((In1-mean1)./sigma1)).^(2*b1));
%层2:
precond = Out1';
Out2 = prod(Out1)';
S_2 = sum(Out2);
%层3:
if S_2~=0
Out3 = Out2'./S_2;
else
Out3 = zeros(1,NumRules);
end
%层4:
Aux1 = [x; 1]*Out3;
%训练数据
a = reshape(Aux1,(Number_signal_in+1)*NumRules,1);
%参数学习
P = (1./lamda).*(P - P*a*a'*P./(lamda+a'*P*a));
ThetaL4 = ThetaL4 + P*a.*e;
ThetaL4_mat = reshape(ThetaL4,Number_signal_in+1,NumRules);
%错误反馈
e3 = [x' 1]*ThetaL4_mat.*e;
denom = S_2*S_2;
%下面自适应产生10个规则的模糊控制器
Theta32 = zeros(NumRules,NumRules);
if denom~=0
for k1=1:NumRules
for k2=1:NumRules
if k1==k2
Theta32(k1,k2) = ((S_2-Out2(k2))./denom).*e3(k2);
else
Theta32(k1,k2) = -(Out2(k2)./denom).*e3(k2);
end
end
end
end
e2 = sum(Theta32,2);
%层一
Q = zeros(Number_signal_in,Number_Fuzzy_rules,NumRules);
for i=1:Number_signal_in
for j=1:Number_Fuzzy_rules
for k=1:NumRules
if Out1(i,j)== precond(k,i) && Out1(i,j)~=0
Q(i,j,k) = (Out2(k)./Out1(i,j)).*e2(k);
else
Q(i,j,k) = 0;
end
end
end
end
Theta21 = sum(Q,3);
%自适应参数调整
if isempty(find(In1==mean1))
deltamean1 = Theta21.*(2*b1./(In1-mean1)).*Out1.*(1-Out1);
deltab1 = Theta21.*(-2).*log(abs((In1-mean1)./sigma1)).*Out1.*(1-Out1);
deltasigma1 = Theta21.*(2*b1./sigma1).*Out1.*(1-Out1);
dmean1 = Learn_rate*deltamean1 + coff*dmean1;
mean1 = mean1 + dmean1;
dsigma1 = Learn_rate*deltasigma1 + coff*dsigma1;
sigma1 = sigma1 + dsigma1;
db1 = Learn_rate*deltab1 + coff*db1;
b1 = b1 + db1;
for i=1:Number_Fuzzy_rules-1
if ~isempty(find(mean1(:,i)>mean1(:,i+1)))
for i=1:Number_signal_in
[mean1(i,:) index1] = sort(mean1(i,:));
sigma1(i,:) = sigma1(i,index1);
b1(i,:) = b1(i,index1);
end
end
end
end
%完成参数学习过程
%并保存参数学习结果
Xt = [reshape(mean1,Number_signal_in*Number_Fuzzy_rules,1);reshape(sigma1,Number_signal_in*Number_Fuzzy_rules,1);reshape(b1,Number_signal_in*Number_Fuzzy_rules,1);reshape(P,((Number_signal_in+1)*NumRules)^2,1);ThetaL4;reshape(dmean1,Number_signal_in*Number_Fuzzy_rules,1);reshape(dsigma1,Number_signal_in*Number_Fuzzy_rules,1);reshape(db1,Number_signal_in*Number_Fuzzy_rules,1);dThetaL4;];
end
out=Xt;
%S函数的第三步,定义各个网络层的数据转换
elseif flag == 3
Feedfor_phase;
%定义整个模糊神经网络的各个层的数据状态
%第一层
x = u(1:Number_inport);
In1 = x*ones(1,Number_Fuzzy_rules);%第一层的输入
Out1 = 1./(1 + (abs((In1-mean1)./sigma1)).^(2*b1));%第一层的输出,这里,这个神经网络的输入输出函数可以修改
%第一层
precond = Out1';
Out2 = prod(Out1)';
S_2 = sum(Out2);%计算和
%第三层
if S_2~=0
Out3 = Out2'./S_2;
else
Out3 = zeros(1,NumRules);%为了在模糊控制的时候方便系统的运算,需要对系统进行归一化处理
end
%第四层
Aux1 = [x; 1]*Out3;
a = reshape(Aux1,(Number_signal_in+1)*NumRules,1);%控制输出
%第五层,最后结果输出
outact = a'*ThetaL4;
%最后的出处结果
out = [outact;Xt];
else
out = [];
endTS模糊控制器的S函数
function [out,Xt,str,ts] = Sfunc_fnn_TS(t,Xt,u,flag,Learn_rate,coffa,lamda,r,vigilance,coffb,arate,Number_signal_in,Number_Fuzzy_rules,x0,Xmins,Data_range,T_samples)
%输入定义
% t,Xt,u,flag :S函数固定的几个输入脚
% Learn_rate :学习度
% coffb :用于神经网络第一层的参数调整
% lamda :神经网络的学习遗忘因子
% Number_signal_in :输入的信号的个数
% Number_Fuzzy_rules :模糊控制规则数
% T_samples :模块采样率
Data_in_numbers = Number_signal_in;
Data_out_numbers = 1;
%整个系统的输入x,误差输入e,以及训练指令的数组的长度
ninps = Data_in_numbers+Data_out_numbers+1;
Number_Fuzzy_rules2 = Number_Fuzzy_rules;
Num_out1 = 2*Number_signal_in*Number_Fuzzy_rules + ((Number_signal_in+1)*Number_Fuzzy_rules2)^2 + (Number_signal_in+1)*Number_Fuzzy_rules2 + 1;
Num_out2 = 2*Number_signal_in*Number_Fuzzy_rules + (Number_signal_in+1)*Number_Fuzzy_rules2;
%S函数第一步,参数的初始化
if flag == 0
out = [0,Num_out1+Num_out2,1+Num_out1+Num_out2,ninps,0,1,1];
str = [];
ts = T_samples;
Xt = x0;
%S函数的第二步,状态的计算
elseif flag == 2
x1 = (u(1:Data_in_numbers) - Xmins)./Data_range;
x = [ x1; ones(Data_in_numbers,1) - x1];
e = u(Data_in_numbers+1:Data_in_numbers+Data_out_numbers);
learning = u(Data_in_numbers+Data_out_numbers+1);
%1的时候为正常工作状态
if learning == 1
NumRules = Xt(1);
NumInTerms = NumRules;
Feedfor_phase;
%最佳参数搜索
New_nodess = 0;
reass = 0;
Rst_nodes = [];
rdy_nodes = [];
while reass == 0 && NumInTerms<Number_Fuzzy_rules
%搜索最佳点
N = size(w_a,2);
node_tmp = x * ones(1,N);
A_AND_w = min(node_tmp,w_a);
Sa = sum(abs(A_AND_w));
Ta = Sa ./ (coffb + sum(abs(w_a)));
%节点归零
Ta(Rst_nodes) = zeros(1,length(Rst_nodes));
Ta(rdy_nodes) = zeros(1,length(rdy_nodes));
[Tamax,J] = max(Ta);
w_J = w_a(:,J);
xa = min(x,w_J);
%最佳节点测试
if sum(abs(xa))./Number_signal_in >= vigilance,
reass = 1;
w_a(:,J) = arate*xa + (1-arate)*w_a(:,J);
elseif sum(abs(xa))/Number_signal_in < vigilance,
reass = 0;
Rst_nodes = [Rst_nodes J ];
end
if length(Rst_nodes)== N || length(rdy_nodes)== N
w_a = [w_a x];
New_nodess = 1;
reass = 0;
end
end;
%节点更新
u2 = w_a(1:Number_signal_in,:);
v2 = 1 - w_a(Number_signal_in+1:2*Number_signal_in,:);
NumInTerms = size(u2,2);
NumRules = NumInTerms;
if New_nodess == 1
ThetaL5 = [ThetaL5; zeros(Number_signal_in+1,1)];
dThetaL5 = [dThetaL5; zeros(Number_signal_in+1,1)];
P = [ P zeros((Number_signal_in+1)*(NumRules-1),Number_signal_in+1);
zeros(Number_signal_in+1,(Number_signal_in+1)*(NumRules-1)) 1e6*eye(Number_signal_in+1); ];
du2 = [du2 zeros(Number_signal_in,1);];
dv2 = [dv2 zeros(Number_signal_in,1);];
end
%层2:
x1_tmp = x1;
x1_tmp2 = x1_tmp*ones(1,NumInTerms);
Out2 = 1 - check(x1_tmp2-v2,r) - check(u2-x1_tmp2,r);
%层3:
Out3 = prod(Out2);
S_3 = sum(Out3);
%层4:
if S_3~=0
Out4 = Out3/S_3;
else
Out4 = zeros(1,NumRules);
end
Aux1 = [x1_tmp; 1]*Out4;
a = reshape(Aux1,(Number_signal_in+1)*NumRules,1);
%层五
P = (1./lamda).*(P - P*a*a'*P./(lamda+a'*P*a));
ThetaL5 = ThetaL5 + P*a.*e;
ThetaL5_tmp = reshape(ThetaL5,Number_signal_in+1,NumRules);
%错误反馈
%层4:
e4 = [x1_tmp' 1]*ThetaL5_tmp.*e;
denom = S_3*S_3;
%层3:
Theta43 = zeros(NumRules,NumRules);
if denom~=0
for k1=1:NumRules
for k2=1:NumRules
if k1==k2
Theta43(k1,k2) = ((S_3-Out3(k2))./denom).*e4(k2);
else
Theta43(k1,k2) = -(Out3(k2)./denom).*e4(k2);
end
end
end
end
e3 = sum(Theta43,2);
%层2
Q = zeros(Number_signal_in,NumInTerms,NumRules);
for i=1:Number_signal_in
for j=1:NumInTerms
for k=1:NumRules
if j==k && Out2(i,j)~=0
Q(i,j,k) = (Out3(k)./Out2(i,j)).*e3(k);
else
Q(i,j,k) = 0;
end
end
end
end
Thetass = sum(Q,3);
Thetavv = zeros(Number_signal_in,NumInTerms);
Thetauu = zeros(Number_signal_in,NumInTerms);
for i=1:Number_signal_in
for j=1:NumInTerms
if ((Out2(i)-v2(i,j))*r>=0) && ((Out2(i)-v2(i,j))*r<=1)
Thetavv(i,j) = r;
end
if ((u2(i,j)-Out2(i))*r>=0) && ((u2(i,j)-Out2(i))*r<=1)
Thetauu(i,j) = -r;
end
end
end
%根据学习结果辨识参数计算
e3_tmp = (e3*ones(1,Number_signal_in))';
du2 = Learn_rate*Thetavv.*e3_tmp.*Thetass + coffa*du2;
dv2 = Learn_rate*Thetauu.*e3_tmp.*Thetass + coffa*dv2;
v2 = v2 + du2;
u2 = u2 + dv2;
if ~isempty(find(u2>v2))
for i=1:Number_signal_in
for j=1:NumInTerms
if u2(i,j) > v2(i,j)
temp = v2(i,j);
v2(i,j) = u2(i,j);
u2(i,j) = temp;
end
end
end
end
if ~isempty(find(u2<0)) || ~isempty(find(v2>1))
for i=1:Number_signal_in
for j=1:NumInTerms
if u2(i,j) < 0
u2(i,j) = 0;
end
if v2(i,j) > 1
v2(i,j) = 1;
end
end
end
end
%WA由学习结果更新
w_a = [u2; 1-v2];
%上面的结果完成学习过程
Xt1 = [NumRules;reshape(w_a,2*Number_signal_in*NumInTerms,1);reshape(P,((Number_signal_in+1)*NumRules)^2,1); ThetaL5;reshape(du2,Number_signal_in*NumInTerms,1);reshape(dv2,Number_signal_in*NumInTerms,1);dThetaL5;];
ns1 = size(Xt1,1);
Xt = [Xt1; zeros(Num_out1+Num_out2-ns1,1);];
end
out=Xt;
%S函数的第三步,定义各个网络层的数据转换
elseif flag == 3
NumRules = Xt(1);
NumInTerms = NumRules;
Feedfor_phase;
u2 = w_a(1:Number_signal_in,:);
v2 = 1 - w_a(Number_signal_in+1:2*Number_signal_in,:);
%层1输出
x1 = (u(1:Data_in_numbers) - Xmins)./Data_range;
%层2输出
x1_tmp = x1;
x1_tmp2 = x1_tmp*ones(1,NumInTerms);
Out2 = 1 - check(x1_tmp2-v2,r) - check(u2-x1_tmp2,r);
%层3输出
Out3 = prod(Out2);
S_3 = sum(Out3);
%层4输出.
if S_3~=0
Out4 = Out3/S_3;
else
Out4 = zeros(1,NumRules);
end
%层5输出
Aux1 = [x1_tmp; 1]*Out4;
a = reshape(Aux1,(Number_signal_in+1)*NumRules,1);
outact = a'*ThetaL5;
out = [outact;Xt];
else
out = [];
end
function y = check(s,r);
rows = size(s,1);
columns = size(s,2);
y = zeros(rows,columns);
for i=1:rows
for j=1:columns
if s(i,j).*r>1
y(i,j) = 1;
elseif 0 <= s(i,j).*r && s(i,j).*r <= 1
y(i,j) = s(i,j).*r;
elseif s(i,j).*r<0
y(i,j) = 0;
end
end
end
return
A05-04