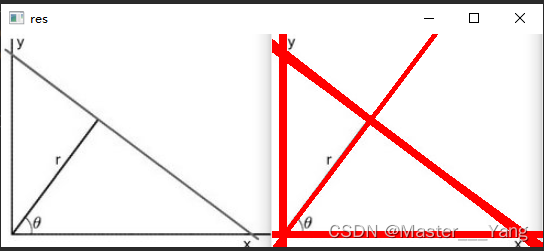
霍夫变换通常用来提取图像的直线和圆等。
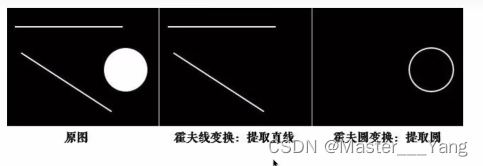
1.霍夫线变换
1.1原理
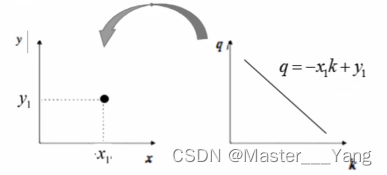
在笛卡尔坐标系下,两点能够确定一条直线。将y=kx+q改写为(k,q)表达式:
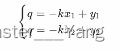
对应的变换通过图像可以表现为:
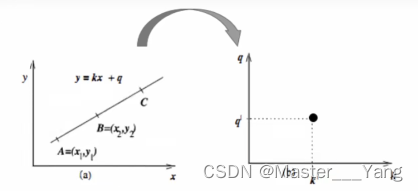
变换后的空间我们叫做霍夫空间。即:笛卡尔坐标系中的一条直线,对应于霍夫空间中的一个点。反过来,同样成立,霍夫空间中的一条线。对应于笛卡尔坐标系中一个点。如下所示:
对于三点的情况:

可以看出如果在笛卡尔坐标系的点共线,那么这些点在霍夫空间中对应的直线交于一点。如果不止存在一条直线时。如下所示:
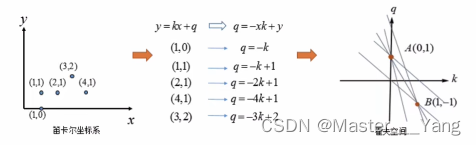
对于上述直线的斜率存在的情况下,用直角坐标系容易解决。对于直线不存在,则需要采用极坐标。
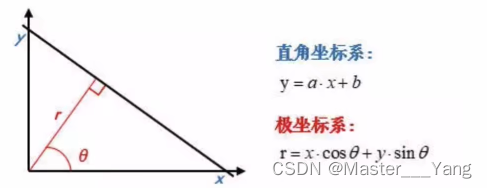
在极坐标下是一样的,极坐标中的点对应于霍夫空间的线,这时的霍夫空间是不在是参数(k, ρ)的空间,而是(ρ,θ)的空间,ρ是原点到直线的垂直距离,θ表示直线的垂线与横轴顺时针方向的夹角,垂直线的角度为0度,水平线的角度是180度。
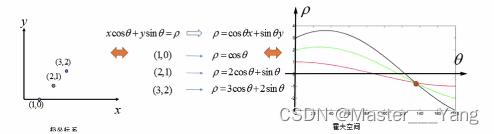
因此我们只需要得到霍夫空间中交点的位置,就可以求出原坐标系下的直线。
1.2霍夫线检测步骤
为了保存霍夫空间中交点的情况,可以使用二维数组进行保存。初始化所有的值均为0,行表示ρ,列表是θ。
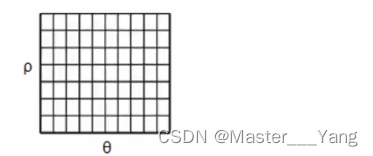
该数组的大小决定了结果的准确性,若希望角度的精度为1度,那就需要180列。对于ρ,最大值为图片对角线的距离,如果希望精度达到像素级别,行数应该与图像的对角线的距离相等。
累加计算:将经过边缘检测的图像,取图像上(x,y)处的点。依次遍历θ从0,1,…180。带入极坐标公式下进行计算,在相应的位置上进行加一。
依次取图像上的点,重复进行上述操作,即可得到最终数组的情况,找到二维数组上大于指定阈值的点,该点就能就可以把图像中的直线给表示出来。
1.3代码实现
cv2.HoughLines(img,rho,theta,threshold)
img:要求是二值化图像或者进行canny边缘检测。
rho,theta:ρ和θ的精度。
threshold:高于该阈值,才认为是直线。
import numpy as np
import cv2
img = cv2.imread("img/lines.png",1)
img2 = np.copy(img)
edges = cv2.Canny(cv2.cvtColor(img,cv2.COLOR_BGR2GRAY), 50,150)
lines = cv2.HoughLines(edges, 1, np.pi / 180, 120)
print(lines)
for line in lines:
rho , theta = line[0]
a = np.cos(theta)
b = np.sin(theta)
x0 = rho * a
y0 = rho * b
x1 = int(x0 + 1000 * (-b))
y1 = int(y0 + 1000 * a)
x2 = int(x0 - 1000 * (-b))
y2 = int(y0 - 1000 * a)
cv2.line(img2, (x1, y1), (x2, y2), (0, 0, 255), 3)
cv2.imshow("res",np.hstack([img,img2]))
cv2.waitKey(0)
自定义简单的霍夫线代码实现:
def houghlines(img, threshold):
theta = 180
rtho = int(np.sqrt(img.shape[0] ** 2 + img.shape[1] ** 2))
arr = np.zeros((rtho, theta), dtype=np.int32)
height, width = img.shape[0:2]
for i in range(height):
for j in range(width):
if img[i][j] != 0:
for k in range(theta):
rou = int(j * np.cos(k * np.pi / 180) + i * np.sin(k * np.pi / 180))
arr[rou][k] = arr[rou][k] + 1
line = []
for i in range(len(arr)):
for j in range(len(arr[i])):
if arr[i][j] > threshold:
line.append([i, j])
return line