本文是李沐老师和王木头老师视频的学习笔记
权重衰退
一般模型的参数越多那么模型的容量就越大(模型能对数据拟合的程度),为了防止模型过拟合有时我们需要降低模型的容量,比如通过限制参数值的范围来到达缩小模型容量的目的。
m
i
n
??
l
(
w
,
b
)
s
u
b
j
e
c
t
??
t
o
∣
∣
w
∣
∣
2
≤
θ
min\; \mathscr{l}(w,b) \quad subject\; to \quad ||w||^2 \leq \theta
minl(w,b)subjectto∣∣w∣∣2≤θ
θ
\theta
θ越小正则项越小
这是一个约束条件为
∣
∣
w
∣
∣
2
≤
θ
||w||^2\leq \theta
∣∣w∣∣2≤θ的条件极值问题,使用拉格朗日乘子法求解,那么构造:
m
i
n
??
l
(
w
,
b
)
+
λ
2
(
∣
∣
w
∣
∣
2
?
θ
)
min\;\mathscr{l}(w,b)+\cfrac{\lambda}{2}\big(||w||^2-\theta\big)
minl(w,b)+2λ?(∣∣w∣∣2?θ)
而对于
λ
\lambda
λ和
θ
\theta
θ知其一就可以解除另一个,所以可以等价为:
m
i
n
??
l
(
w
,
b
)
+
λ
2
∣
∣
w
∣
∣
2
min\;\mathscr{l}(w,b)+\cfrac{\lambda}{2}||w||^2
minl(w,b)+2λ?∣∣w∣∣2
可证明
λ
→
∞
w
?
→
0
\lambda\rightarrow\infty\quad w^*\rightarrow 0
λ→∞w?→0使用
λ
\lambda
λ控制
θ
\theta
θ
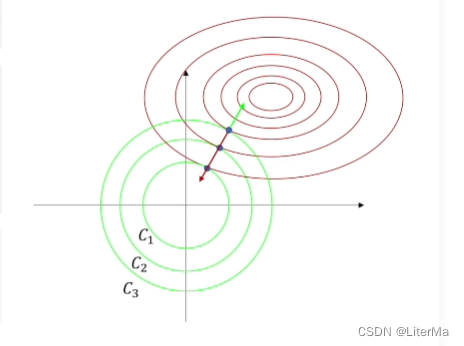
如下图中
C
C
C代表
θ
\theta
θ个方向坐标轴为
w
w
w的大小,可见
C
C
C越大
w
w
w越小则起到了控制模型容量的作用。
那么梯度的计算和参数更新就变为了:
梯度:
?
?
w
(
l
(
w
,
b
)
+
λ
2
∣
∣
w
∣
∣
2
)
??
=
??
l
(
w
,
b
)
?
w
+
λ
w
\cfrac{\partial}{\partial w}\big ( \mathscr l(w,b)+\cfrac{\lambda}{2}||w||^2 \big )\;=\; \cfrac{\mathscr l (w,b)}{\partial w}+\lambda w
?w??(l(w,b)+2λ?∣∣w∣∣2)=?wl(w,b)?+λw
提取公因数后参数更新公示:
w
t
+
1
=
(
1
?
η
λ
)
w
t
?
η
?
l
(
w
t
,
b
t
)
?
w
t
w_{t+1}=(1-\eta\lambda)w_t-\eta\cfrac{\partial \mathscr l(w_t,b_t)}{\partial w_t}
wt+1?=(1?ηλ)wt??η?wt??l(wt?,bt?)?
当
λ
η
<
1
\lambda\eta<1
λη<1时叫做权重衰退。
丢弃法
丢弃法对输出的元素
x
i
x_i
xi?做如下扰动:
{
0
,
p
r
o
b
a
b
i
l
i
t
y
??
p
x
i
1
?
p
,
o
t
h
e
r
i
s
e
\left\{\begin{matrix}0,\quad probability \;p \\\cfrac{x_i}{1-p},\quad otherise\end{matrix}\right.
?
?
??0,probabilityp1?pxi??,otherise?
经过此扰动对于每个
x
i
x_i
xi?的期望仍为
x
i
x_i
xi?
E
(
x
i
′
)
=
0
?
p
+
(
1
?
p
)
?
x
i
1
?
p
=
x
i
E(x_i^{'})=0\cdot p+(1-p)\cdot \cfrac{x_i}{1-p}=x_i
E(xi′?)=0?p+(1?p)?1?pxi??=xi?
丢弃法将一些隐藏层的输出随机的置为0,从而来控制模型复杂度,其丢弃概率为控制模型复杂度的超参数。
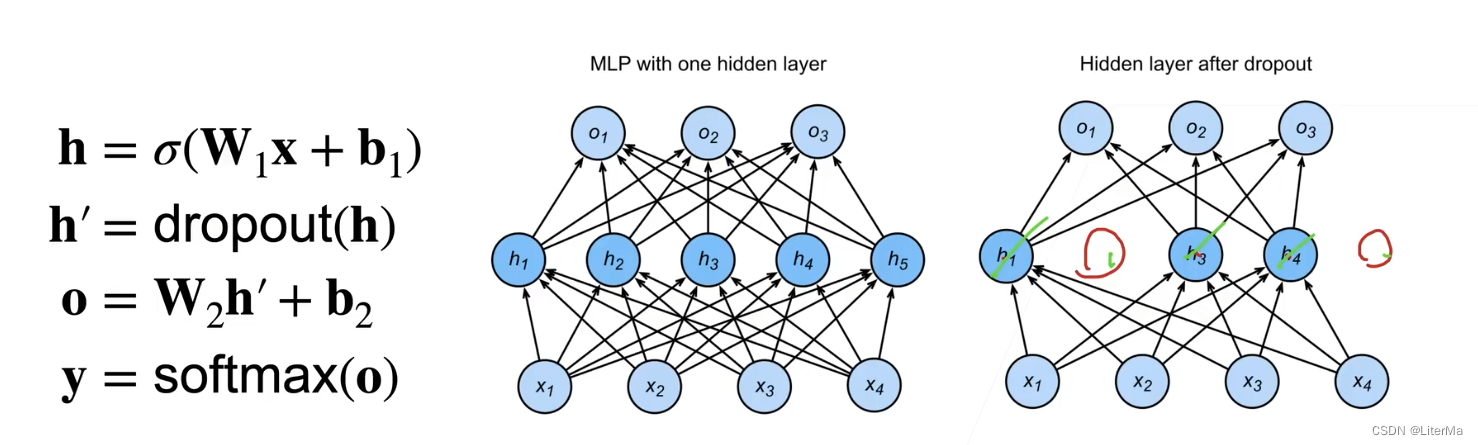
dropout只在训练时启用,用于调整参数,在推理时并不使用。