本文是接着上一篇深度学习之 7 深度前馈网络_水w的博客-CSDN博客
目录
自动梯度计算
手动使用链式法则计算每个参数的导数并编程实现非常繁琐且极易出错。可使用计算 机实现参数的自动梯度计算,其方法可分为 数值微分 、 符号微分 和 自动微分 三类。
1、数值微分
用数值的方法来计算函数
𝑓 𝑥
的导数,函数
𝑓(𝑥)在点𝑥处的导数定义为:
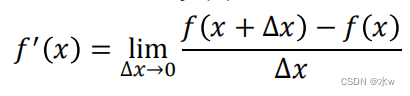
?在实际应用中,经常使用下面的方式来计算梯度,以减小截断误差,
? ?𝑥 难以确定,太小会引起舍入误差,太大则增加截断误差;? 虽然实现非常简单,但实用性较差;? 计算复杂性高,因为需要为每个参数单独施加扰动,若参数数量为 𝑁 ,则复杂度为 𝑂(𝑁 2 )
2、符号微分
? 一种基于符号计算(代数计算)的自动求导方法,用计算机来 求解带变量的数学表达式? 变量被看作符号, 不需要代入具体的值 ,输入和输出都是数学表达式;? 包括基于规则的化简、因式分解、微分、积分、解代数方程、解常微分方程等运算;? 编译时间长;? 需要专门的数学计算语言;? 很难调试;? 对于深层复合函数,输出的表达式非常冗长,形成表达式膨胀(expression swell);
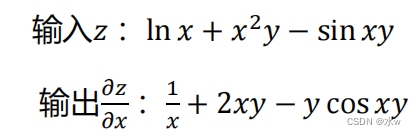
3、自动微分
? 一种介于数值微分和符号微分之间的方法????????? 数值微分强调一开始直接代入数值近似求解,而符号微分强调直接对表达式进行求解,最后才代入数值;????????? 自动微分将符号微分法应用于最基本的算子,比如常数、幂函数、指数函数、对数函数、三角函数等,将其代入数值,保留中间结果,最后再应用于整个函数;? 灵活性高????????? 微分求解过程对用户是透明的;????????? 不需要专门的数学语言和编程;????????? 采用图的方式进行计算,可以做很多优化;
4、计算图
? 将复合函数分解为一系列基本操作,并以图的形式连接起来;
? 是数学运算的图结构表示,每个非叶子节点代表一个基本操作,每个叶子节点代 表一个输入变量或常量;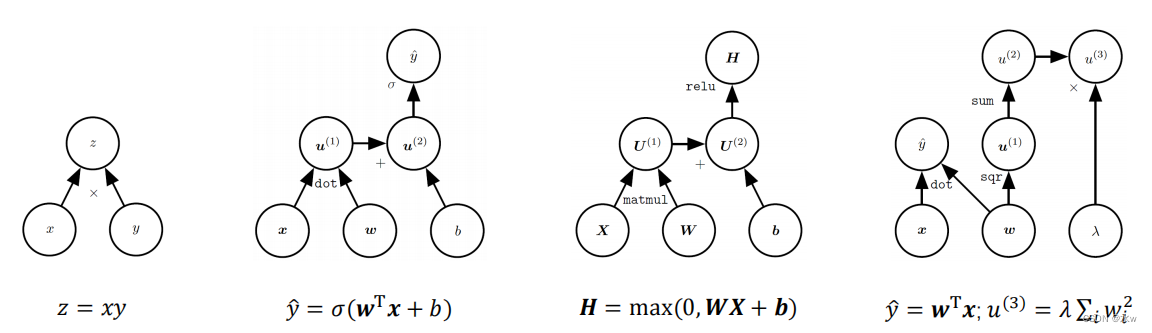
实例?:
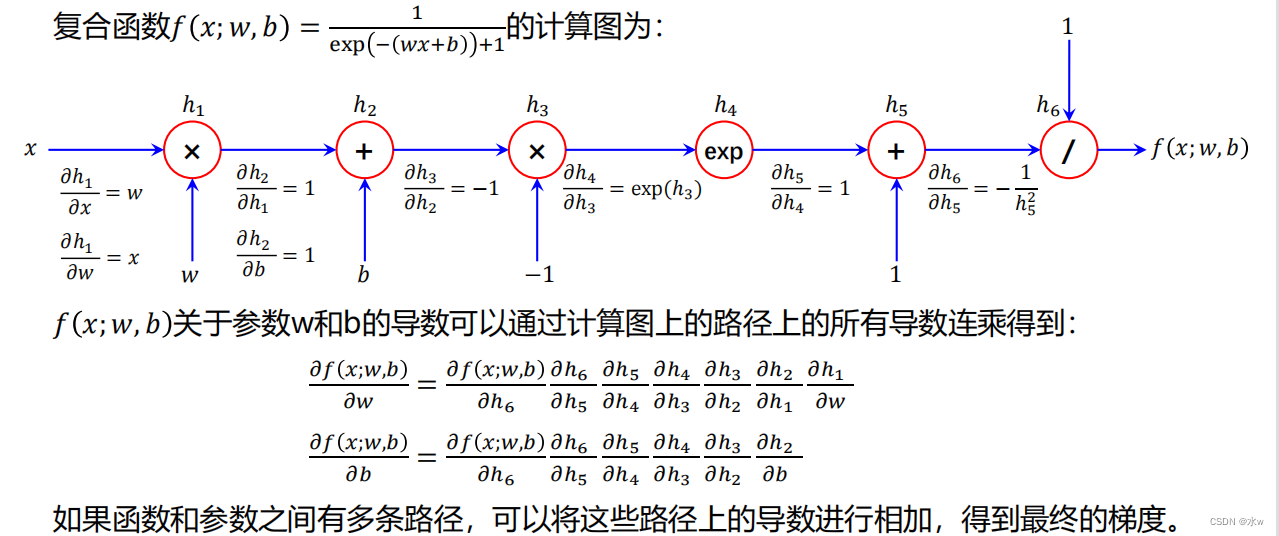
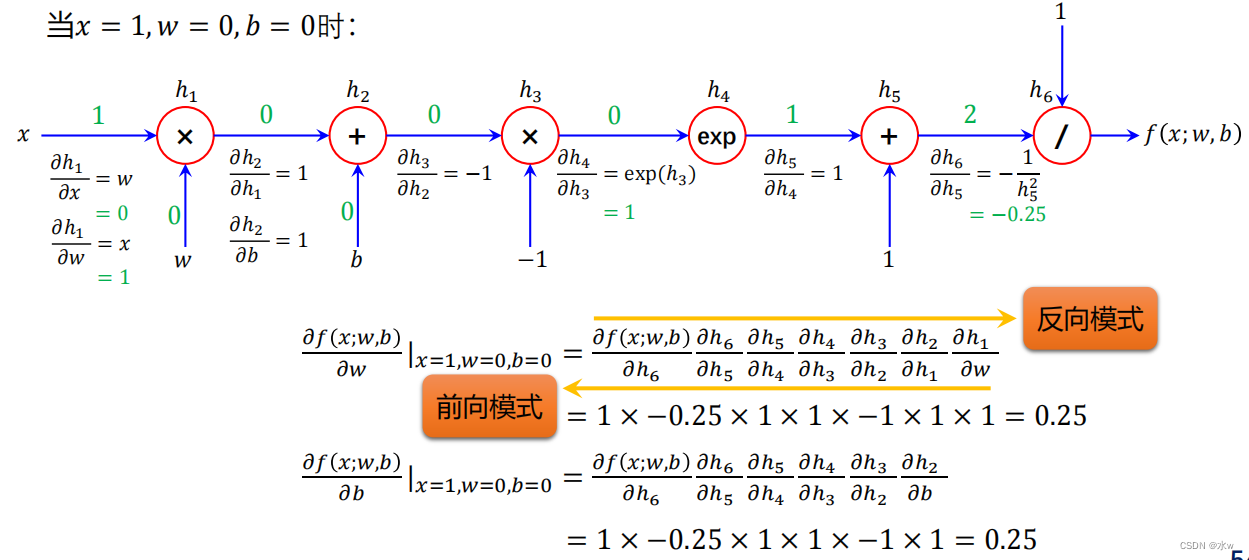 ?
?
正则化单隐层MLP计算图: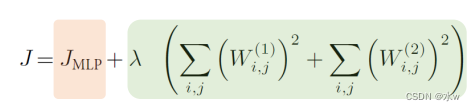 ??
??
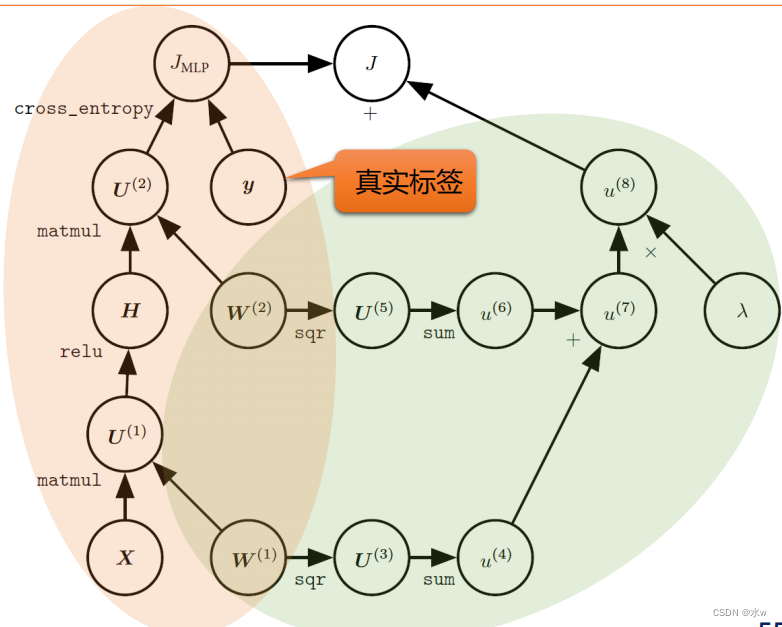 ?
?
?5、静态计算图、动态计算图
在当前深度学习框架中,Theano和Tensorflow采用的是静态计算图, 而DyNet、Chainer和PyTorch采用的是动态计图。Tensorflow 2.0 也开始支持动态计算图。? 静态计算图(Static Computational Graph)????????? 在编译时构建计算图,构建好后在程序运行时不能改变????????? 在构建时可以进行优化、并行能力强????????? 灵活性较差? 动态计算图(Dynamic Computational Graph)????????? 在程序运行时动态构建计算图????????? 不容易优化,当不同输入所使用的网络结构不一样时,难以并行计算????????? 灵活性比较高
神经网络参数优化的主要问题
1、非凸优化
?
神经网络的优化问题是一个非凸优化问题
以一个最简单的1-1-1结构的两层网络为例:
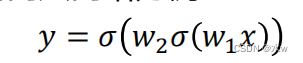
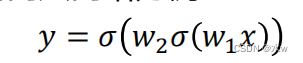
其中𝑤1和𝑤2为网络参数,𝜎(?)为Logistic激活函数。
给定一个样本
1,1
,
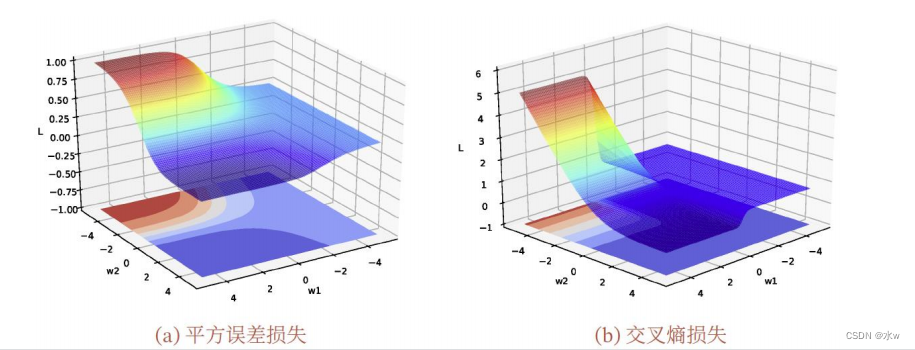
平方误差损失
和
交叉熵损失
与参数
𝑤
1
和
𝑤
2
的关系如下图:
2、梯度消失
? 误差在反向传播过程中不断衰减甚至消失?
?
回顾误差反向传播的迭代公式:
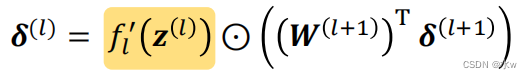
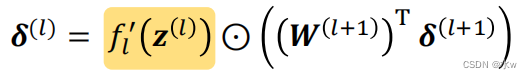
?误差在每一层传播时都要乘以该层激活函数的导数。
?
当采用
Sigmoid
型激活函数时,导数为:
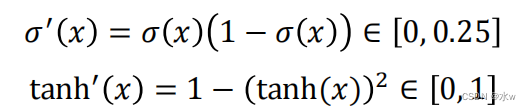
?二者的导数的值域都小于或者等于1,在饱和区的导数更接近于0,这就会造成梯度的不断衰减,甚至消失,使得整个网络很难训练。
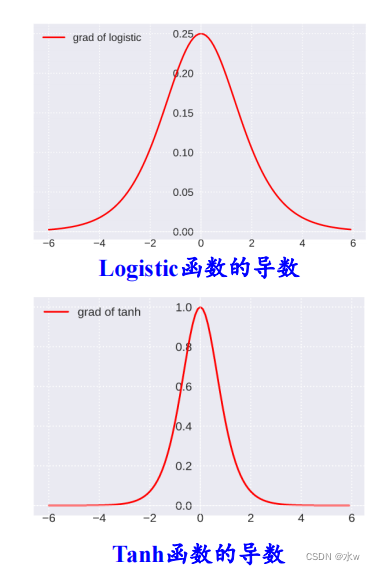
?