KS和roc曲线
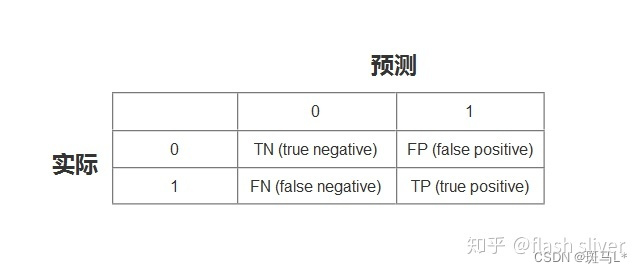
- TN:将负类预测为负类(真负类)
- FN:将正类预测为负类(假负类)
- TP:将正类预测为正类(真正类)
- FP:将负类预测为正类(假正类)
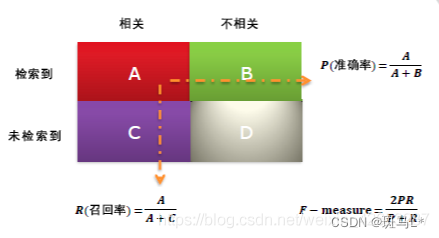
精确率:是针对我们预测结果而言的,它表示的是预测为正的样本中有多少是真正的正样本。
召回率:是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。
准确率 (Accuracy)
测试样本中正确分类的样本数占总测试的样本数的比例。
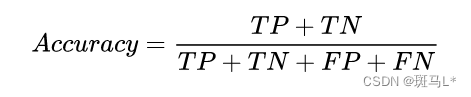
精确率 (Precision)
准确率又叫查准率,测试样本中正确分类为正类的样本数占分类为正类样本数的比例。
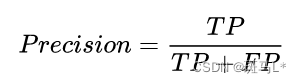
召回率 (Recall)
召回率又称查全率,测试样本中正确分类为正类的样本数占实际为正类样本数的比例。
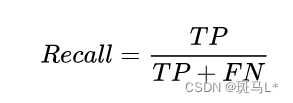
F1 值
F1 值是查准率和召回率的加权平均数。F1 相当于精确率和召回率的综合评价指标,对衡量数据更有利,更为常用。
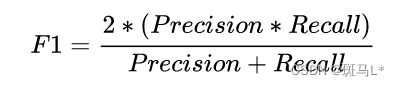
真正类率(TPR)
预测的正类中实际正实例占所有正实例的比例。(跟召回率一样的计算公式)
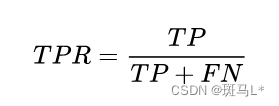
负正类率(FPR)
预测的正类中实际负实例占所有负实例的比例。
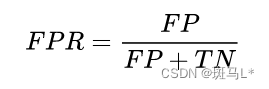
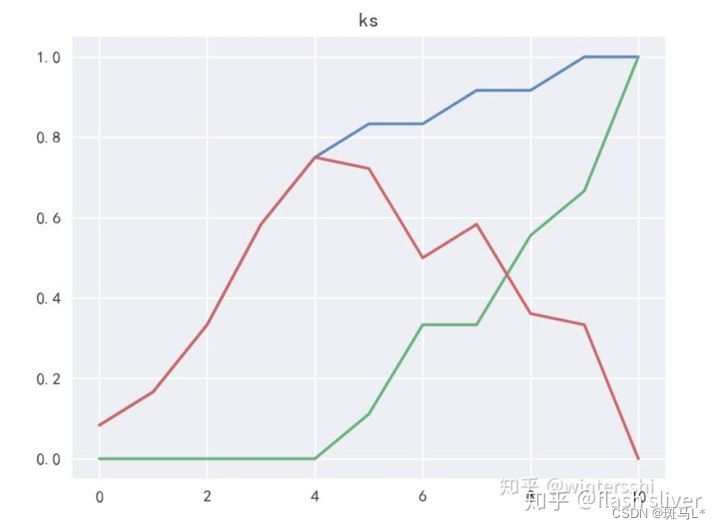
KS曲线
我们训练出来的模型,一般不是直接给出是正类还是负类的结果,给的是为正类的概率,我们还需要选择一个阈值,实例通过模型得到的概率大于阈值,判断为正类,小于阈值判断为负类。也就是说阈值的不同,以上的各个指标的值也是不同的。把阈值看成自变量,以上TPR、和FPR看成因变量,在二维坐标系里面做关系曲线,这就是KS曲线。
KS值
我们想要评估模型的能力,在阈值不同的情况下,TPR和FPR 又不一样,突然迷惘起来,这个时候,需要找到一个唯一评判标准,最值有唯一性,上图红色部分表示TPR-FPR,那我们就用最高点作为模型能力的评估标准吧!!对,没有错,最高点就是所谓的KS值,我们用KS值来作为评估模型区分能力的指标,KS值越大,模型的区分能力越强。公式如下:
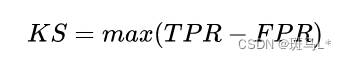
ROC 曲线
ROC的全称是“受试者工作特征”(Receiver Operating Characteristic)曲线。
还是以上的TPR和FPR值,以上我们知道了KS值能表示模型的区分能力,我们只在阈值等于KS值时,觉得模型是好的,这样忽视掉了阈值取其他值的情景,有没有一种评估标准,无关阈值的取值呢?
在实际应用场景中,模型预测了一个样本集,在预测为正类中,我们当然希望的是,预测为正类的样本中,实际也为正类样本的比例越高越好,预测为正类的样本中,实际为负类样本的比例越小越好,也就是说,TPR越大越好,最好等于1,FPR越小越好,最好等于0,可是没有这么完美的事情,TPR变大的同时,FPR也会变大。数学家是聪明的,同时变化是吧,变化的速度总是有区别的吧?
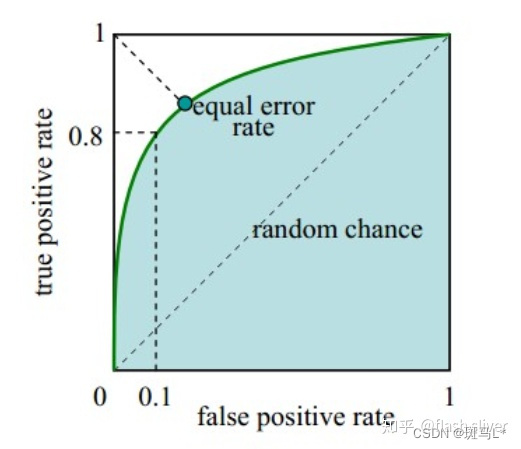
我们随机取很多阈值,得到很多FPR和TPR。用 X轴表示FPR,Y轴表示TPR,绘制上图曲线,这个曲线就是ROC曲线。(0,0)和(1,1)这两个坐标点根据实际情况,我们知道是固定的,假如两者的变化率是一样的,也就是说是一条过(0,0) 和(1,1) 的直线,此时斜率为1,也就是说随着阈值的变化,FPR和TPR 都同等程度变化。绘制出了曲线,是否可以用曲线的特性来表示模型的能力呢?我们希望得到的是:
- FPR 变化快的时候,TPR变化慢.
- FPR变化慢的时候,变化快。
到这里,我们又找到了一个评估模型的指标,对,就是图中的阴影面积,观察发现,我们可以用这个阴影面积的大小,来反应上面我们希望得到的特性,这个阴影面积的大小叫做AUC值。
AUC
AUC(Area Under Curve) 被定义为ROC曲线下的面积,因为ROC曲线一般都处于y=x这条直线的上方,所以取值范围在0.5和1之间,使用AUC作为评价指标是因为ROC曲线在很多时候并不能清晰地说明哪个分类器的效果更好,而AUC作为一个数值,其值越大代表分类器效果更好。需要注意的是AUC是一个概率值,当随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的分数将这个正样本排在负样本前面的概率就是AUC值。所以,AUC的值越大,当前的分类算法越有可能将正样本排在负样本值前面,既能够更好的分类。
评分卡 分箱 WOE IV
分箱
- 把离散特征的类别进行分箱二次分类(比如,中国的所有城市,通过分箱划分为县区市地区等),可以让模型快读迭代。
- 对于连续特征,分箱会降低数据的噪声影响。分箱后的数据有很强的稳定性。
- 将连续数据分箱后,进行哑变量或独热编码的处理,每个特征中的每一类别就有了权重,这样相当于为模型引入的非线性,能够提升模型的拟合能力。
一句话概括:分箱主要是为了避免连续型变量的取值过于稀疏从而影响模型去学习其中的“好坏”规律。

无监督分箱:等频分箱和等距分箱。等频分箱是使每箱的样本数相等,等距分箱是使每个箱的宽度相等。
有监督分箱:卡方分箱、决策树分箱、Best-KS分箱
- 卡方分箱:是一种自底向上的(即基于合并的)数据离散化方法。 先算出单变量每个取值的卡方,再把卡方值相近的取值合并到一个箱里。
- 决策树分箱:与卡方分箱不同,决策树分箱是一种自上而下的分箱方法。通过计算信息增益,我们可以对单个自变量的划分生成决策树。决策树的分裂节点就是每个箱的边界。最终得到的叶子节点就是每一个箱。
- Best-KS分箱也是一种从上到下的分箱方法。和决策树使用信息增益判断是否分箱不同,Best-KS分箱一般选择KS值最大的地方做分裂点。
不论采用哪种分箱方式,我们最终得到的都是各区间的分裂点。在Python中,它很可能是一个列表的形式,像这样:[5,20,35,40,60]。仅仅得到分裂点是不够的,我们还需要对原始数据进行相应的处理。这就引出了下面的两个概念:
WOE与IV值
WOE的全称是“Weight of Evidence”,即证据权重。WOE是对原始自变量的一种编码形式。
WOE的两种公式理解
1.坏人的分布减去好人的分布。

2.每个箱中的坏人好人之间的比值 与 整个特征中坏人好人之间的比值 的差异。

WOE越大,以上这两种差异就越大。原始数据中好人,坏人都混在一起,是无法分清的。我们通过分箱的操作,可以把好人坏人尽可能的分割开,而WOE就是衡量分箱后,好人坏人的分割程度的。
IV是Information Value的缩写。它其实是单变量所有WOE取值的加权平均,用来衡量这个变量整体的预测能力,或者说“区分度”。IV值越大,则变量的区分效果越好。
逻辑回归模型转化为评分卡:
由逻辑回归的基本原理,我们将客户违约的概率表示为p,则正常的概率为1-p。因此,可以设:
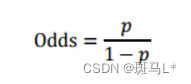
此时,客户违约的概率p可表示为:
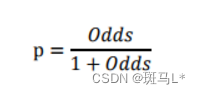
根据逻辑回归计算可得:
评分卡设定的分值刻度可以通过将分值表示为比率对数的线性表达式来定义,即可表示为下式:
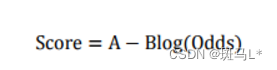
其中,A和B是常数。式中的负号可以使得违约概率越低,得分越高。通常情况下,这是分值的理想变动方向,即高分值代表低风险,低分值代表高风险。
式中的常数A、B的值可以通过将两个已知或假设的分值带入计算得到。通常情况下,需要设定两个假设:
(1)给某个特定的比率设定特定的预期分值;
(2)确定比率翻番的分数(PDO)
根据以上的分析,我们首先假设比率为x的特定点的分值为P。则比率为2x的点的分值应该为P-PDO。代入式中,可以得到如下两个等式:
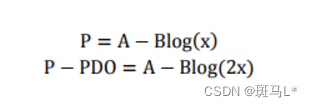
假设我们期望x=(bad/good)=5%时的分值为50分,PDO为10分(即每增加10分bad/good比例就会缩减一半),代入式中求得:B=14.43,A=6.78,这个时候bad/good=10%时score=40
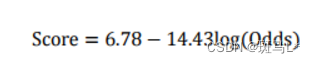
评分卡刻度参数A和B确定以后,就可以计算比率和违约概率,以及对应的分值了。通常将常数A称为补偿,常数B称为刻度。
则评分卡的分值可表达为:
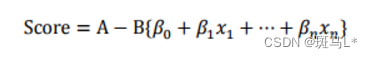
式中:变量x1…xn是出现在最终模型中的自变量,即为入模指标。由于此时所有变量都用WOE转换进行了转换,可以将这些自变量中的每一个都写(βiωij)δij的形式:
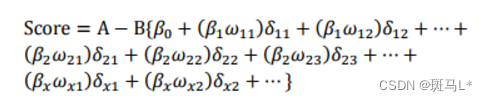
式中ωij 为第i行第j个变量的WOE,为已知变量;βi为逻辑回归方程中的系数,为已知变量;δij为二元变量,表示变量i是否取第j个值。上式可重新表示为:
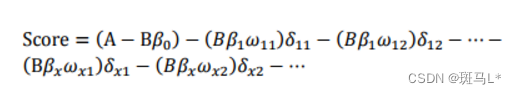
此式即为最终评分卡公式。如果x1…xn变量取不同行并计算其WOE值,式中表示的标准评分卡格式,基础分值等于(A?Bβ0);由于分值分配公式中的负号,模型参数β0,β1,…,βn也应该是负值;变量xi的第j行的分值取决于以下三个数值:
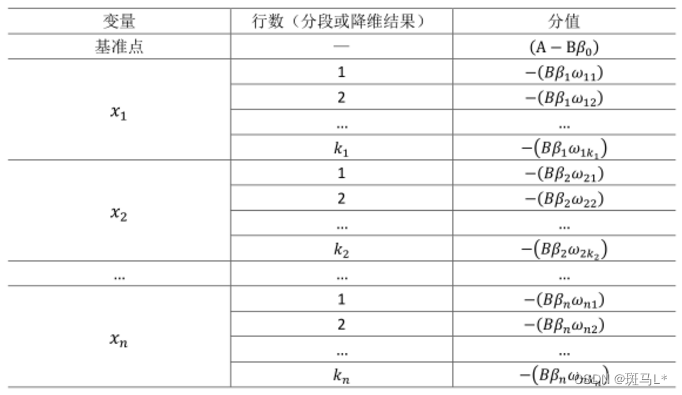
总的来说整体的思想就是根据每个变量的系数进行评分转换,好的变量我们给与高的评分,坏的变量给与低分或者负分。
T检验:比较两个平均数的差异是否显著
F检验:检查不同样本的总体方差是否相同的一种方法
实战代码:
数据为财务相关指标数据,第一列是公司代码,中间是相关指标,最后一列是是否违约数据。
# 加载所需的Python包
import numpy as np
import pandas as pd
from scipy import stats
import scorecardpy as sc
from sklearn.linear_model import LogisticRegression
# 获得数据
data = pd.read_excel(r'E:\工作\逻辑回归过程文档\datadata.xlsx')
#将指标名称改为中文
data.columns = ["COMPCODE","TOTASSET","净资产收益率","总资产收益率","每股收益盈利能力","销售净现率","每股现金净流量","流动比率","速动比率","现金债务比","权益债务比","每股净资产","营运资金与总资产的比率","应收账款周转率","存货周转率","总资产周转率","销售增长","利润增长","资本增长","长期债务与营运资金的比率","资产留存收益的比率","资产负债率"," Log(总资产)","log(净资产)","TARGET"]
#填补缺失值
for i in data.columns:
data[i] = data[i].fillna(stats.mode(data[i])[0][0]) #众数填充
#data = data.fillna(method='ffill') # ffill---前填充;bfill--后填充
data =data[~data.isin([np.nan, np.inf, -np.inf]).any(1)] #处理NAN INF值
compcode = data['COMPCODE']
data=data.drop('COMPCODE', axis=1) #取出公司代码,模型输入不需要
data=data.drop('TOTASSET', axis=1) #总资产 多的指标字段
# Traditional Credit Scoring Using Logistic Regression
# 基于逻辑回归的传统信用回归
# filter variable via missing rate, iv, identical value rate
# 通过数据缺失率、IV值、相同值来过滤变量
#dt_s = sc.var_filter(data, y="TARGET")
dt_s=data
'''
def var_filter(dt, y, x=None, iv_limit=0.02, missing_limit=0.95,
identical_limit=0.95, var_rm=None, var_kp=None,
return_rm_reason=False, positive='bad|1')
'''
# var_rm:强制删除变量的名称
# var_kp:强制保留变量的名称
# return_rm_reason:是否返回每个变量被删除的原因
# positive:坏样本的标签
# # 正态性检验
# X = data.loc[:, data.columns != 'TARGET']
# from scipy.stats import kstest
# kw_x=pd.DataFrame()
# for i in X.columns:
# norm = kstest(X[i], 'norm')
# print(norm)
# print(norm.pvalue)
# if norm.pvalue<0.5:
# t = stats.ttest_1samp(X[i],0)
# print(t) #T检验
# if t.pvalue > 0.5:
# data=data.drop(i, axis=1)
# else:
# kw_x.append(X[i])
# kw = stats.kruskal(X[i]).pvalue
# print(kw) #KW检验
# if kw.pvalue > 0.5:
# data=data.drop(i, axis=1)
# #print(data.columns)
# #多重共线性检验
# from statsmodels.stats.outliers_influence import variance_inflation_factor
# X = data.loc[:, data.columns != 'TARGET']
# vif = [variance_inflation_factor(X.values, X.columns.get_loc(i)) for i in X.columns]
# print(vif)
# # 当VIF<10,说明不存在多重共线性;当10<=VIF<100,存在较强的多重共线性,当VIF>=100,存在严重多重共线性
# print(len(X.columns))
# print(len(vif))
# for i in range(len(X.columns)):
# if vif[i] > 10:
# data = data.drop(X.columns[i], axis=1)
# print(data.columns)
#
# from sklearn.preprocessing import StandardScaler
# from sklearn.cluster import KMeans
# from pyecharts.charts import HeatMap
# import pyecharts.options as opts
# from copy import copy
# # 指标筛选
# # #相关性
# X = data.loc[:, data.columns != 'TARGET']
# class cal_corr:
#
# def __init__(self, df, n_clusters=5, threshold=0.7):
# # 对所有变量矩阵先进行处理
# self.df = self.handle_df(df.copy())
# # Kmeans聚类的时候指定聚成几类
# self.n_clusters = n_clusters
# # 相关性筛选时的阈值
# self.threshold = threshold
# # 变量的相关矩阵存下来
# self.corr = None
#
# @property
# def corr_matrix(self):
# # 变量的相关矩阵
# return self.corr
#
# @property
# def corr_pairs(self):
# # 变量两两间的相关系数对
# return self.pairs
#
# def handle_df(self, df):
# '''
# 先处理一下变量矩阵:
# 类别型变量做编码处理
# 缺失值填充为中位数
# 所有变量做一下均一化处理
# '''
#
# for item in df.select_dtypes(include=["object"]):
# df[item] = df[item].astype('category').cat.codes
#
# df = df.fillna(df.median())
# df = pd.DataFrame(StandardScaler().fit_transform(df), columns=df.columns)
# print(df.shape)
# return df
#
# def order_by_kmeans(self):
# '''
# 根据Kmeans聚类结果对变量进行排序
# '''
#
# kk = KMeans(n_clusters=self.n_clusters)
# res = kk.fit_predict(self.df.T)
#
# self.df = self.df.append(pd.Series(res, index=self.df.columns), ignore_index=True)
# self.df.sort_values(by=self.df.shape[0] - 1, axis=1, inplace=True)
# self.df.drop(self.df.shape[0] - 1, inplace=True)
#
# print(self.df.shape)
#
# def corr_heat_map(self):
# '''
# 计算相关矩阵,并使用pyecharts的heat_map呈现
# '''
#
# self.order_by_kmeans()
#
# self.corr = self.df.corr(method="pearson")
# self.corr = self.corr.round(3)
# self.corr = self.corr.apply(lambda x: abs(x))
# myvalues = []
# for i in range(len(self.corr.index)):
# for j in range(len(self.corr.index)):
# tmp = [i, j, self.corr.iloc[i, j]]
# myvalues.append(copy(tmp))
# self.__setattr__('pairs', myvalues)
#
# heat_map = HeatMap(init_opts=opts.InitOpts(width="1440px", height="1440px")) \
# .add_xaxis(list(self.corr.columns)) \
# .add_yaxis("corr", list(self.corr.index), myvalues) \
# .set_global_opts(
# title_opts=opts.TitleOpts(title="模型变量相关性"),
# datazoom_opts=[opts.DataZoomOpts(is_show=True, is_realtime=True), ],
# visualmap_opts=opts.VisualMapOpts(min_=-1.2, max_=1.2, pos_right=20),
# toolbox_opts=opts.ToolboxOpts(is_show=True),
# xaxis_opts=opts.AxisOpts(type_="category", is_scale=True, is_inverse=True,
# axislabel_opts=opts.LabelOpts(is_show=True, rotate=-60)),
# yaxis_opts=opts.AxisOpts(is_scale=True, is_inverse=False,
# axislabel_opts=opts.LabelOpts(is_show=True, position="right")),
# tooltip_opts=opts.TooltipOpts(is_show=True)) \
# .set_series_opts(label_opts=opts.LabelOpts(is_show=True, position="insideBottom"))
#
# heat_map.render()
#
# def drop_hight_corr(self):
# '''
# 根据上述算法,删除相关性高的变量
# '''
#
# cor_pair = self.pairs
# cor_pair.sort(key=lambda x: x[2], reverse=True)
# del_pair = []
# del_col = []
# for item in cor_pair:
# if (item[0] == item[1]) | (set(item[:2]) in del_pair) | (item[0] in del_col) | (item[1] in del_col):
# continue
#
# if item[2] > self.threshold:
# c1 = self.corr.iloc[item[0], [x for x in range(self.corr.shape[0]) if x not in del_col]].mean()
# c2 = self.corr.iloc[item[1], [x for x in range(self.corr.shape[0]) if x not in del_col]].mean()
#
# del_col.append(item[0] if c1 > c2 else item[1])
# del_pair.append(set(item[:2]))
# else:
# break
#
# del_col_name = self.corr.iloc[:, del_col].columns
#
# return list(del_col_name)
#
# c = cal_corr(X, n_clusters=5, threshold=0.5)
# # 在当前路径下产生的render.html文件即为相关矩阵热力图
# c.corr_heat_map()
# del_col = c.drop_hight_corr()
# #print(del_col) 被删掉的指标
# for i in range(len(del_col)):
# data=data.drop(del_col[i], axis=1)
#
#
#
# dt_s=data
lable = dt_s.columns
print(lable)#输出 保留的指标
# breaking dt into train and test
# 将DataFrame分成训练集和测试集
train, test = sc.split_df(dt_s, 'TARGET').values()
# def split_df(dt, y=None, ratio=0.7, seed=186)
# 该函数的ratio默认为0.7,即按照7:3对数据集进行分割。ratio可以随意进行设置,比如[0.5,0.2]
# woe binning ------
# 根据woe值进行分箱
bins = sc.woebin(dt_s, y="TARGET")
#sc.woebin_plot(bins) #sc.woebin_plot()可以画出变量分箱之后的Bi_variate图,这里的坏样本率图展示了每一箱的好坏样本数、样本占比、坏样本率,比较清晰明了。
'''
def woebin(dt, y, x=None,
var_skip=None, breaks_list=None, special_values=None,
stop_limit=0.1, count_distr_limit=0.05, bin_num_limit=8,
# min_perc_fine_bin=0.02, min_perc_coarse_bin=0.05, max_num_bin=8,
positive="bad|1", no_cores=None, print_step=0, method="tree",
ignore_const_cols=True, ignore_datetime_cols=True,
check_cate_num=True, replace_blank=True,
save_breaks_list=None, **kwargs):
'''
# woebin支持决策树分箱、卡方分箱、自定义分箱,默认的WOE值计算是用坏样本率/好样本率,
# 这个可以通过参数postive进行调整。如果某一箱只有好样本或者坏样本,会对缺失的类别赋予0.99进行调整,方便计算woe值。
# 重要参数含义如下:
# var_skip:指定不需要分箱的变量。
# breaks_list:分割点的List。对分箱进行调整的时候用。可以进行自定义分箱
# special_values:指定单独的箱。
# count_distr_limit:分箱结果中最小占比。默认0.05
# stop_limit:当IV值的增加值小于stop_limit或者卡方值小于qchisq(1-stoplimit, 1)时停止分割。
# bin_num_limit:最大分箱数。
# method:分箱方法,可以有"tree" or “chimerge”。
# ignore_const_cols:是否忽略常数列。
# check_cate_num:检查分类变量中类别数是否大于50。
# replace_blank:将空值替换为None。
# binning adjustment
# 分箱调整a
# # adjust breaks interactively
# # 有交互地进行重组调整
#breaks_adj = sc.woebin_adj(dt_s, "TARGET", bins)
# # or specify breaks manually
# # 或者手动进行重组调整
# breaks_adj = {
# 'age.in.years': [26, 35, 40],
# 'other.debtors.or.guarantors': ["none", "co-applicant%,%guarantor"]
# }
#bins_adj = sc.woebin(dt_s, y="TARGET", breaks_list=breaks_adj)
# converting train and test into woe values
# 将测试集和训练集转换为woe值
bins_adj=bins
train_woe = sc.woebin_ply(train, bins_adj)
test_woe = sc.woebin_ply(test, bins_adj)
y_train = train_woe.loc[:,'TARGET']
X_train = train_woe.loc[:,train_woe.columns != 'TARGET']
y_test = test_woe.loc[:,'TARGET']
X_test = test_woe.loc[:,train_woe.columns != 'TARGET']
# logistic regression ------
# 逻辑回归 -----
lr = LogisticRegression(penalty='l1', C=0.9, solver='saga', n_jobs=-1)
lr.fit(X_train, y_train)
print(lr.coef_)
print(lr.intercept_)
#
# X = bins_adj.loc[:, bins_adj.columns != 'TARGET']
# y = bins_adj.loc[:, bins_adj.columns == 'TARGET']
# y_pred = lr.predict(X)
# result = pd.DataFrame(y)
# result['predict']=y_pred
# result.index=list(compcode)
# result.to_excel(r'E:\工作\评分模型过程文档\predict2.xlsx')
# print(len(compcode)) #1197
# print(len(bins_adj)) #22
# predicted proability
# 可能性预测
train_pred = lr.predict_proba(X_train)[:,1]
test_pred = lr.predict_proba(X_test)[:,1]
# performance ks & roc ------
# ks 和 roc 的性能表现 -----
train_perf = sc.perf_eva(y_train, train_pred, title = "train")
test_perf = sc.perf_eva(y_test, test_pred, title = "test")
# score ------
# 得分 -----
card = sc.scorecard(bins_adj, lr, X_train.columns, points0=600, odds0=1/19, pdo=80)
# def scorecard(bins, model, xcolumns, points0=600, odds0=1/19, pdo=50, basepoints_eq0=False)
# scorecard()函数的参数含义如下:
# bins:分箱信息。woebin()返回的结果。
# model:模型对象。
# points0:基础分,默认为600。 odds:好坏比,默认为1:19
# pdo:比率翻番的倍数,默认为50。
# basepoints_eq0:如果为True,则将基础分分散到每个变量中。
# credit score
# 信用得分
train_score = sc.scorecard_ply(train, card, print_step=0)
test_score = sc.scorecard_ply(test, card, print_step=0)
all_score = sc.scorecard_ply(dt_s, card, print_step=0)
# print(train_score)
# print(test_score)
all_score['COMPCODE']=list(compcode)
#all_score.to_excel(r'E:\工作\评分模型过程文档\card.xlsx') #输出评分到excel
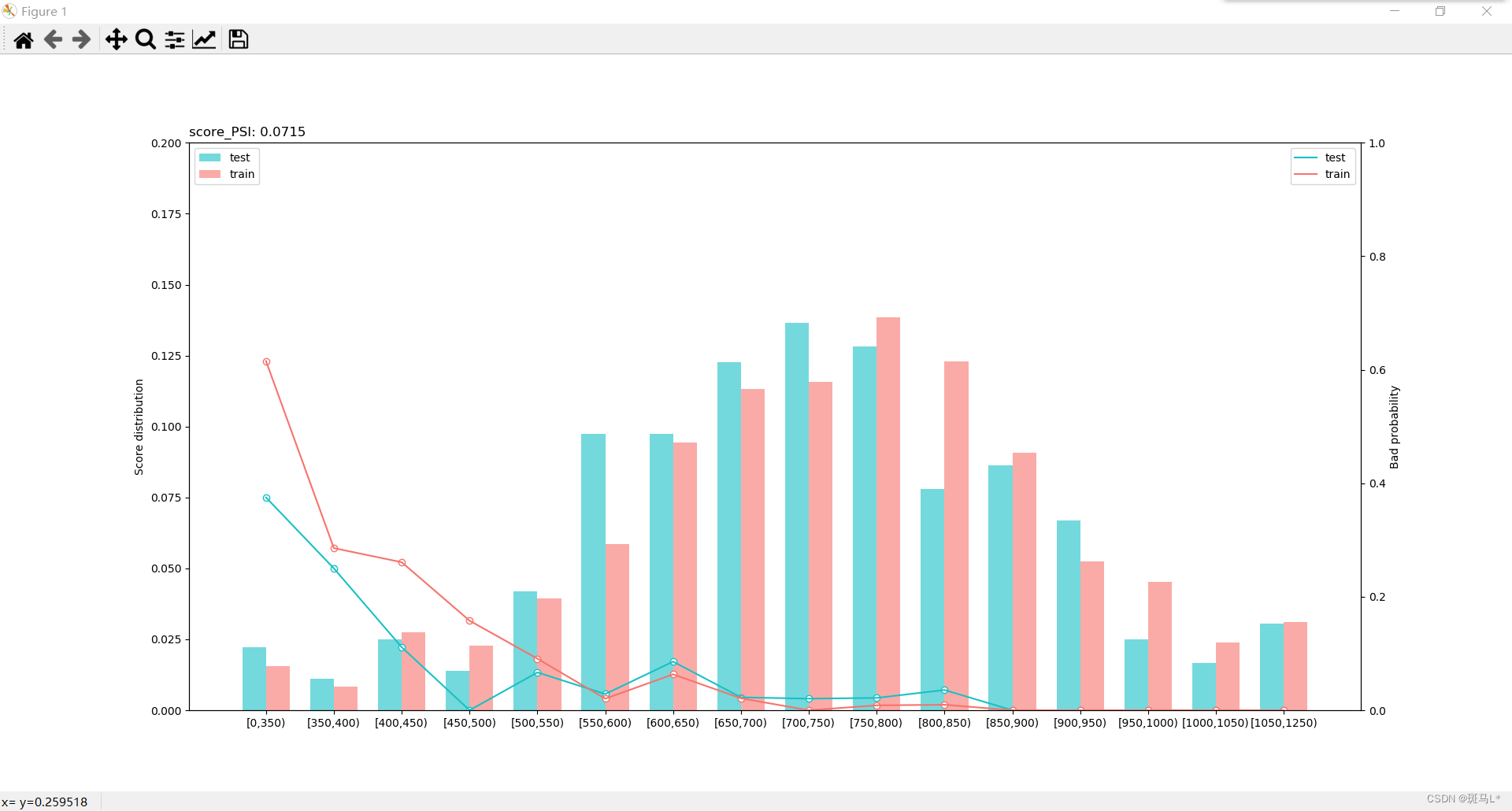
# psi 绘图
#
sc.perf_psi(
score = {'train':train_score, 'test':test_score},
label = {'train':y_train, 'test':y_test}
)
评分结果如下:
可以看到随着评分增加违约概率降低。