目录
我的主页:晴天qt01的博客_CSDN博客-数据分析师领域博主
目前进度:第四部分【机器学习算法】
聚类算法的分类
-Exclusive vs.Non-Exclusive(Overlapping)的聚类方法
聚类方法可以分为排他的聚类方法和非排他的聚类方法,排他的聚类方法,相当于一个资料点,只能属于于一个群。非排它的聚类方法,一个资料点可以属于多个群
例如overlapping就是属于非排他的聚类方法。
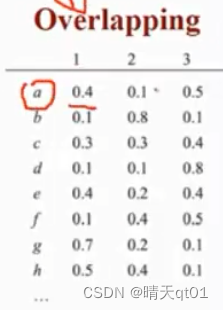
这里代表的含义是1,a对应属于群体的概率,0.4就是属于1群的概率,0.1是属于2群的概率,0.5是属于3群的概率
因为有时候一个数据点,它和2个群的距离都很近,可以它离1最近,但是其实离2页很近,这个就会产生概率值。
但是因为排他法的实际操作很容易,属于排他法的运用还是比较多,比如我们说的k-means方法。
非排他的方法不多,比较出名的是EM,它产生的结果就是上面的图。
如果我们将排他性的方法进行细分的话,就可以分为层次聚类法和划分聚类法
它们都是属于排他聚类的两大类,其实除了EM几乎都是排他聚类法。
这里说明几个比较好用,并且可以囊括大部分情况的方法。
层次聚类算法(统计根据)
单一聚类法、完全链结法、平均链结法、中心法、word’s法
划分聚类法
K-means法、Kmedoids法、SOM法(神经网络的聚类方法)、两步法
它们的差异在哪呢,比如我们选择有5群资料,层次聚类法就是将最接近的两笔数据分为1群,那么他就由5群变为4群,然后它又会计算4群的距离,然后合并两群,变成3群,最后全部合并
他是一次一次的进行划分。
划分聚类法呢就不是这样,他是通过提前划分好几群,例如我现在要划分为3群,那它就会一次性把3群聚类给你。
通常划分聚类法要比层次聚类法要好,所以大多的工具都会提供划分聚类算法。
层次算法出现在统计工具比较多。
而我们会把剩下的方法分为2类,
第一类是模糊聚类法(非排他方法)
EM(expectation maximization)
密度聚类法(一种特殊的排他方法)
以密度为基本的,一般是根据数据的形状来做聚类。之后会和大家细说
DBSCAN
层次聚类的算法,
层次聚类的算法主要是看距离矩阵(也叫相异性矩阵)的下三角,斜对角的距离一定都是0(一样的数据肯定距离为0)
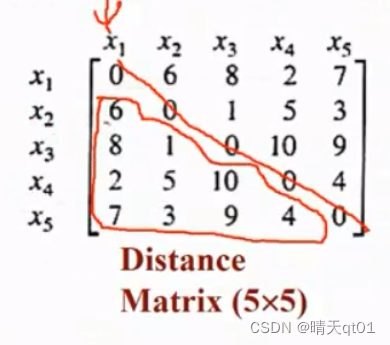
然后我们通过这个距离矩阵,来说第一个层次聚类的方法:
单一聚类法(single link)

我们可以发现,x2和x3的距离矩阵最小,然后是1和4的距离矩阵最小,所以2和3会优先被分类,然后轮到1和4,这个图其实还有一个Y轴,代表距离,距离是1的时候,2和3被分类到一群。距离是2的时候被1和4倍分类到一群。
然后我们再找下一个距离最近的,也就是3,那我们就会把5和3聚到一类,这时2和3已经是一类了,所以在距离3的时候,二者被聚为一类。
接下来我们在找距离为4的,也就是5和4,这时235已经是一个群了,14也是一群,然后把他们聚类为4的地方。
如果将资料分为两群,就在距离为3到4之间砍一刀,14一群,523一群。
分成3群就是在距离2到3之间。以此类推。
这就是单一聚类法
完全链结法
还有一种方法是完全链结法complete Link。
首先我们说明一下完全链结法是什么,就是每个点之间都有线连接,连接之后聚为一群,最终形成完全图,
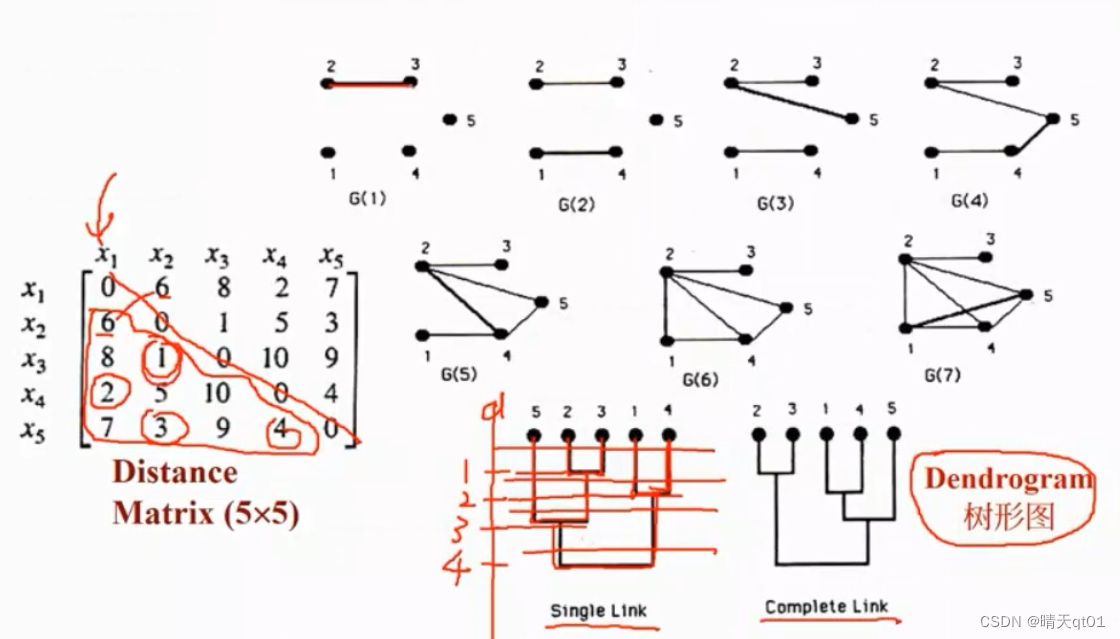
因为刚开始2和3的距离最短,所以2和3会聚为一群,然后1和4也会聚为一群,到这里方法与单一聚类法还是蛮类似的。
然后我们连接下一个距离最近的点,也就是2和5,5想要加入2,3的群体,但是没有形成完全图,5和3的连接还没出现就不能构成群。所以5暂时没法加入23,我们连接下一个点,也就是5和4,在连接下一个点2和4,因为1和3没有和4形成完全图,所以也不能成为一类。接下来距离为6的,1和2连接起来,代表我们要形成14和23的连接,但是3还没和4连接,所以不能融合。接下来长度为7的,1和5,15代表,5要加入14类的连接,这时145以及形成完全连接,所以5号加入14的连接。
这个就是完全链结法
我们来看看完全链结法和单一图像法的差别在哪,从上面来看他们的差异不大,主要就是5这个点加入的位置在哪。它是加入14好还是23好。
以我们的视角来看5加入那个好,如果是单一聚类法,因为5与2近就将5分类到23,不考虑5和3的距离是5。所以5加入23其实是不好的,一个3一个九,差距太远。
5加入14,它和1的距离是7和4的距离是4,那么他们彼此之间的距离就比较短,所以5加入14相对来说比较好。
所以我们看,完全链结法,运行时间久,它主要目的是为了让每个点之间的距离不要太远的群。
我们这边是运用图来解释,实际上运用它不会这么做。因为这么做花的时间比较久。
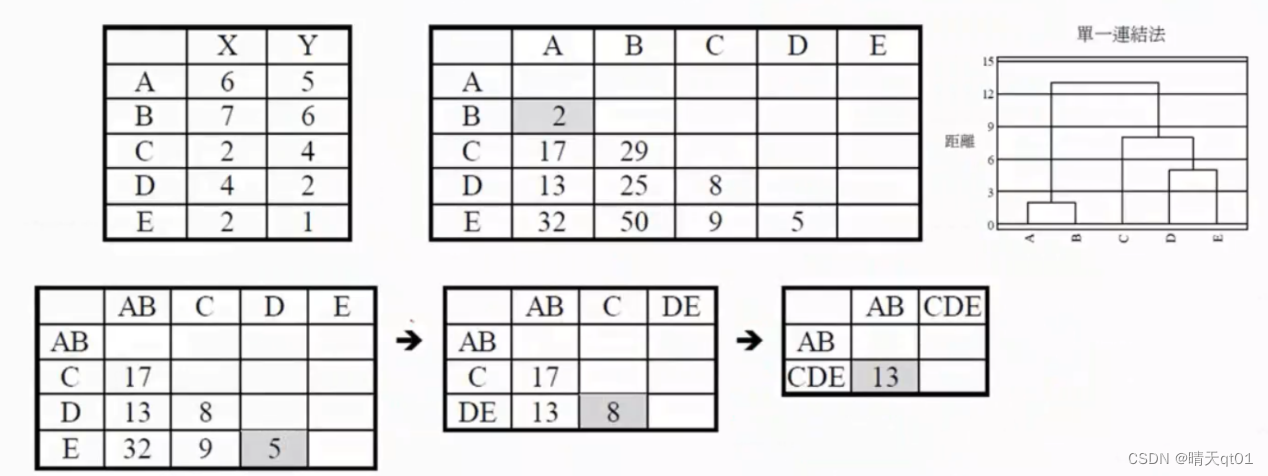
我们这里左上角的图表是一个有5个记录,2个输入字段的数据,我们将求出它的距离矩阵,欧式距离,但是我们不开根号,直接使用平方和。
我们看A和C的距离,6-2的平方加上5-4的平方。刚好17。
用不开根号的欧式距离来作为我们聚类的距离,对结果其实无影响。我们单一链结法就会把最小的距离拿出来,这里面A和B的距离是2,所以我们优先把AB合成一群,在把AB合成一群之后,我们要更新我们的距离矩阵 那么这时AB和CDE的距离怎么算呢,其实就是计算A和C距离和B和C的距离取最小值。CE也是以此类推
然后我们再去寻找最小的值。发现D和E,于是我们把D和E合成一类。
然后再次更新我们的距离矩阵,DE这个新群和ABC的距离也是一样,去D和E中与ABC距离的最小值。最后的最小值就也是一样的
在说明一下完全链结矩阵
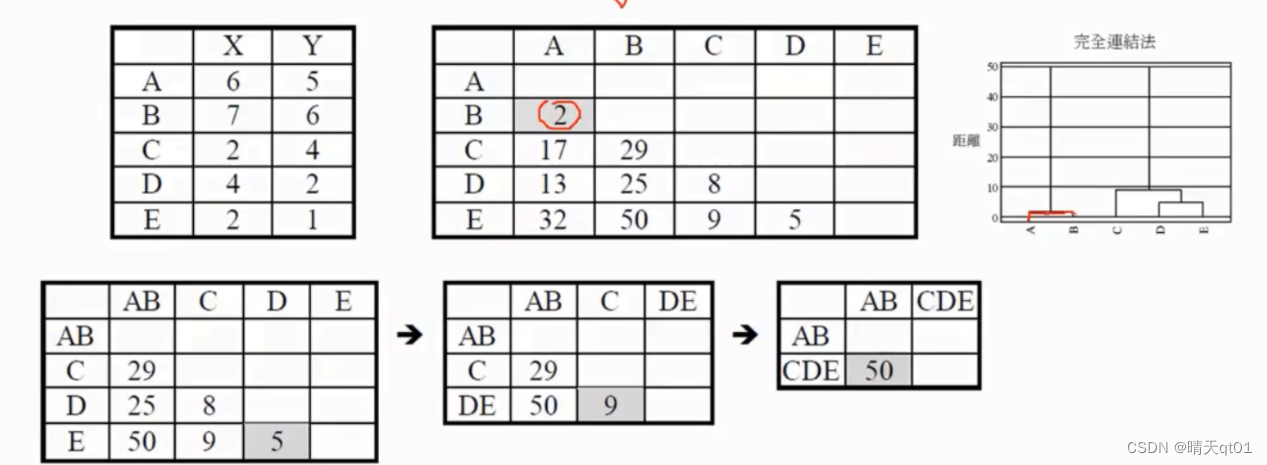
先把AB合并,然后这时,我们采用的是AB与CDE距离最大值,所以我们可以发现单一聚类法和完全链结法,一个是条件最宽松的聚类法,一个是条件最严格的聚类法。
然后我们在聚合DE,还是一样,求DE和AB,C的距离。接下来再取最小值进行合并。
这个就是完全链结法,实际上没有去求完全图。
平均链结法
还有一个是average法,那既然有最大值的完全链结法,有最小值的单一聚类法。自然会有,平均值的聚类法
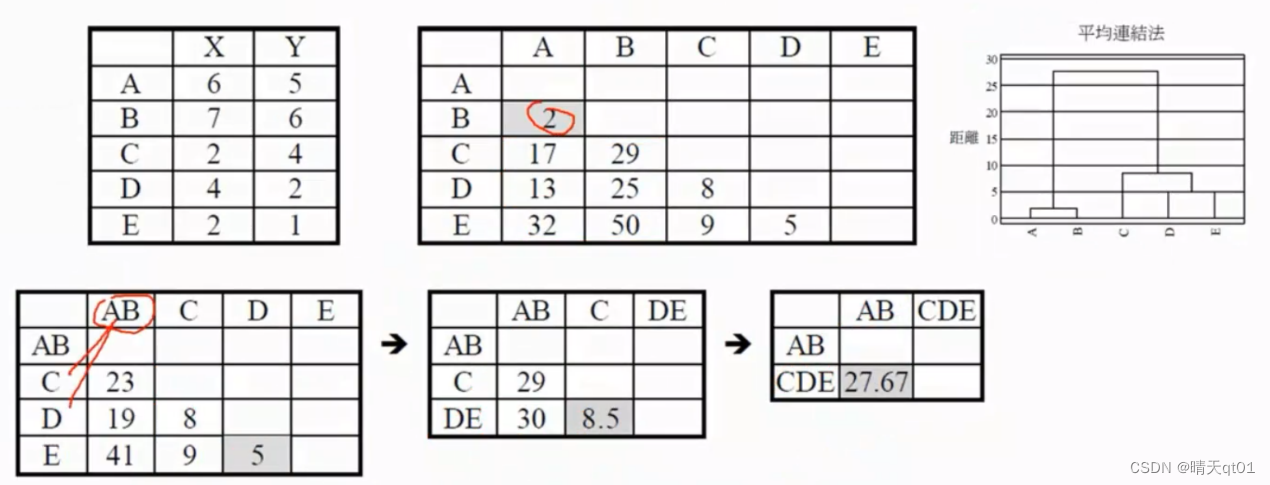
取最小值,然后取平均值。然后再找最小值,在距离。
中心链结法
还有一种方法,叫中心法,这个值是利用中心法求得的,首先,它会把A和B合成一群。

这里把AB合成一群之后,我们将求出对应的原始数据该是多少,然后再求距离矩阵。
AB合为一群之后,AB的X和Y就变成了原本二者的平均值。,然后再计算距离矩阵,AB和C的距离就是6.5-2的平方加上5.5-4的平方。结果就是22.5
然后我们再选择最小值,是DE的距离最小进行合并,这里需要注意的点是CDE的矩阵不是C和DE群的平均值,而是原始数据的3个数和除以3.
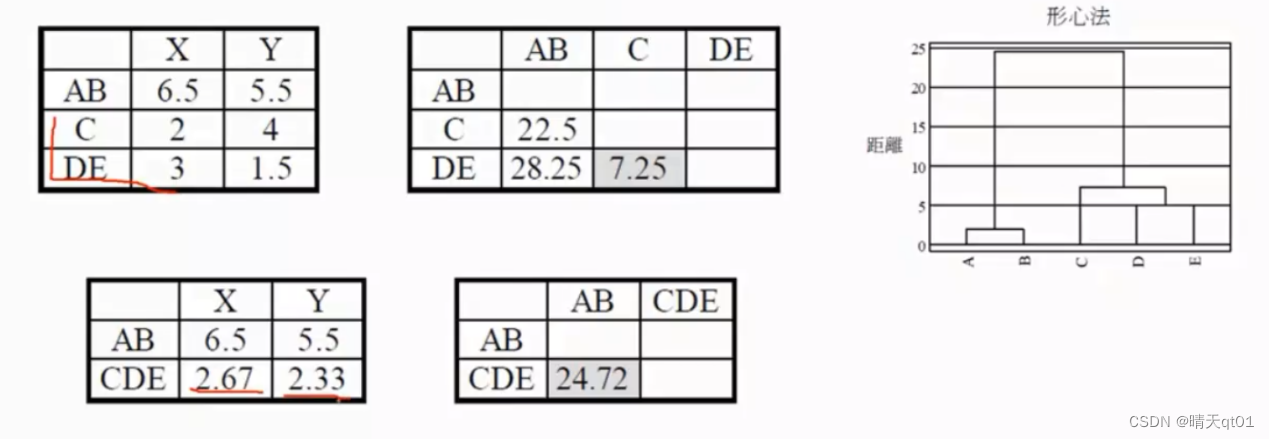
他是以群中心来代替群。
Ward’s法
这是层次聚类里最好用的方法,但是它跑的数据也比较久,为什么它效果好呢,因为它是直接使用一个指标。
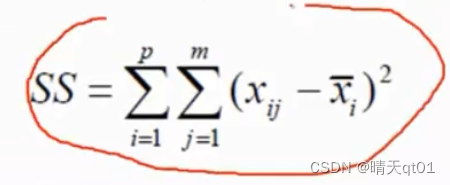
这个指标一般是用来衡量聚类好坏的指标,指标的意义是数据与群中心的平方和的差值
比如现在有两个群,一个群有3个点,一个群有2个点。每个数据与群中心的平方和,也就是与群中心的距离不开根号把这5个平方和相加就是我们的SS值,它就是用来评估聚类的好坏,而我们的Ward’s法就是直接把这个评估的指标用来分析。找到最好的指标,选出最好的聚类。不过耗费的时间也是最久的

这里再说明一下word’s的方法。
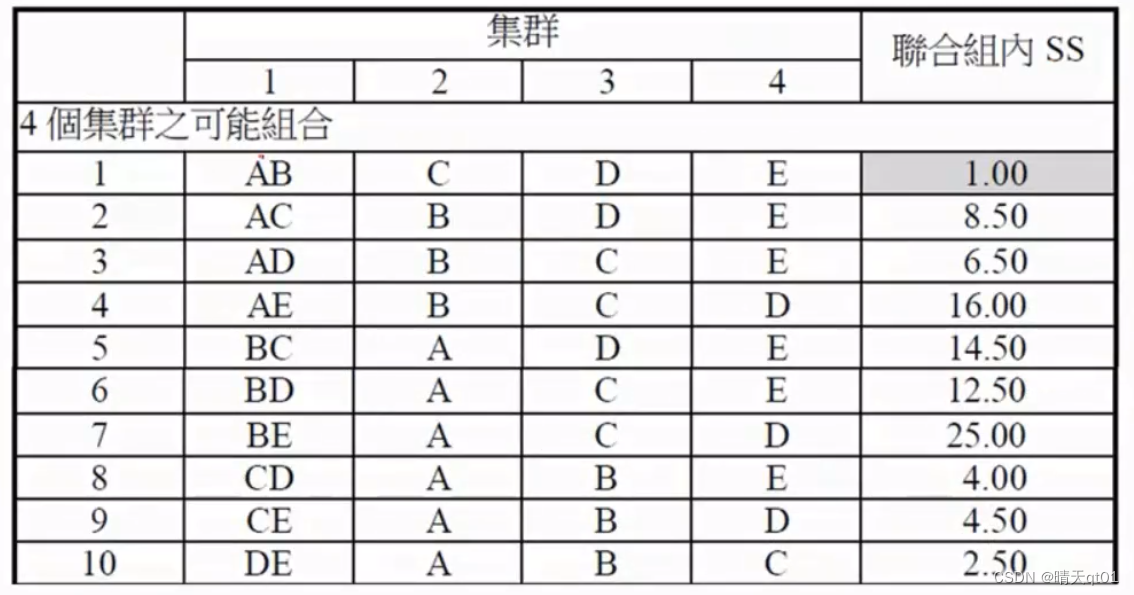
这里是分成4群的几种可能,一共有10种,我们查看SS的值,找到最小的,然后我们就选这个为我们的4群,就成功把5群聚类为4群了,然后我们接着把4群聚类为3群
C43一共6种可能

还是一样,我们计算每种可能的SS值。,然后选出它作为本次聚类的结果,然后再求下一次运作过程。
它的效果是最好的,它一定能找到最好的聚类结果,但是他的运行速度也是很慢很慢。
总结:层次聚类法中,平均链结法和ward’s法效果最好,单一聚类法效果最差。
这里是大多情况,不是绝对的。
Partitioning Methods又优于Hierarchical Methods
然后是划分聚类法中的两步法,这是通过K-means聚类先把数据聚成很多的小群。然后再用分层方法,比如ward’s法或者平均链结法等等进行划分
Methods最后决定群集数,
如何确定群集数呢,这边讲一个最简单的群集数判断法:

我们一般会用陡坡图来判断,横坐标是集群数,纵坐标的SS值或者距离等系数,一般群集数越小,点到群中心的距离会越大,这是正常现象,如果都是现象变化还好,但是出现巨大的变化就说明误差值暴增,我们就会选择把群集数分为2群。