朴素贝叶斯 (Naive Bayes）
前言
提示：这里可以添加本文要记录的大概内容：
例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。
提示：以下是本篇文章正文内容，下面案例可供参考
一、贝叶斯定理
1.1定理推导
条件概率就是事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为P(A|B)，读作“在 B 发生的条件下 A 发生的概率”。
我们可以从条件概率的定义推导出贝叶斯定理。根据条件概率的定义，在事件 B 发生的条件下事件 A 发生的概率为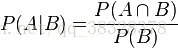
同样地，在事件 A 发生的条件下事件 B 发生的概率为：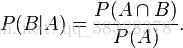
由上述概率我们可以得到：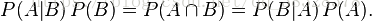
这个引理有时称作概率乘法规则。上式两边同除以 P(B)，若P(B)是非零的，我们可以得到贝叶斯定理:
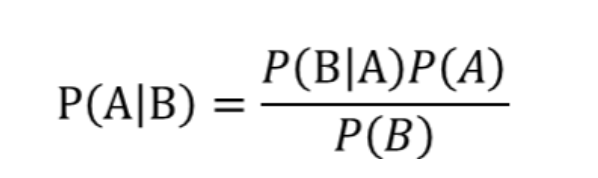
1.2贝叶斯定理例子
- 计算贝叶斯定理P(A|B)
二、朴素贝叶斯
- 朴素贝叶斯基础理论
原始的贝叶斯定理最大的问题在于联合概率密度函数的估计，首先需要根据经验来假设联合概率分布，其次当属性很多时，训练样本往往覆盖不够，参数的估计会出现很大的偏差。为了避免这个问题，朴素贝叶斯（naive Bayes）采用了“属性条件独立性假设”，即样本数据的所有属性之间相互独立。这样类条件概率p（x | c ）可以改写为：
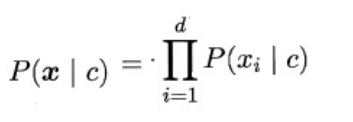
每个样本估计类条件概率P(C|X)变成为每个样本的每个属性估计类条件概率P(C|X)。
相比原始贝叶斯，朴素贝叶斯基于单个的属性计算类条件概率更加容易操作，需要注意的是：若某个属性值在训练集中和某个类别没有一起出现过，这样会抹掉其它的属性信息，因为该样本的类条件概率被计算为0。因此在估计概率值时，常常用进行平滑（smoothing）处理，拉普拉斯修正（Laplacian correction）就是其中的一种经典方法，具体计算方法如下：
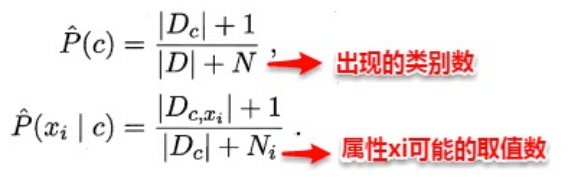
当训练集越大时，拉普拉斯修正引入的影响越来越小。对于贝叶斯分类器，模型的训练就是参数估计，因此可以事先
将所有的概率储存好，当有新样本需要判定时，直接查表计算即可。
1.高斯朴素贝叶斯（GaussianNB)
在高斯朴素贝叶斯中，每个特征都是连续的，并且都呈高斯分布。高斯分布又称为正态分布。图画出来以后像一个倒挂的钟，以均值为轴对称，如下图所示：
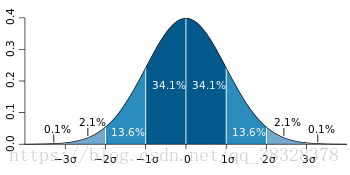
GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布:
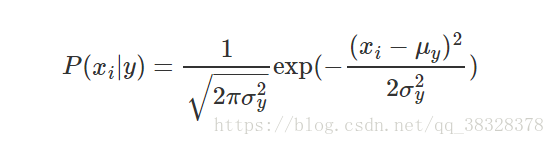
参数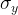 
和 
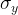使用极大似然法估计为：
# 高斯朴素贝叶斯
from sklearn import datasets
iris = datasets.load_iris()
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
clf = clf.fit(iris.data, iris.target)
y_predict=clf.predict(iris.data)
print('target=')
print(iris.target)
print('predict=')
print(y_predict)
print("高斯朴素贝叶斯，样本总数： %d 错误样本数 : %d" % (iris.data.shape[0],(iris.target != y_predict).sum()))
输出为：
target=
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
predict=
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1
1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 1 2 2 2 2
2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
高斯朴素贝叶斯，样本总数： 150 错误样本数 : 6
2.多项分布朴素贝叶斯（MultinomialNB）
MultinomialNB实现服从多项分布数据（multinomially）的贝叶斯算法，是一个经典的朴素贝叶斯文本分类中使用的变种（其中的数据是通常表示为词向量的数量，虽然TF-IDF向量在实际项目中表现得很好），对于每一个y来说，分布通过向量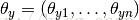 
参数化，n是类别的数目（在文本分类中，表示词汇量的长度）
表示标签i出现的样本属于类别y的概率 
。
参数 
是一个平滑的极大似然估计，即相对频率计数：
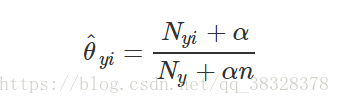
表示标签 i 在样本集中属于类别 y 的数目
表示在所有标签中类别 y 出现的数目
# 多项分布朴素贝叶斯
from sklearn import datasets
iris = datasets.load_iris()
from sklearn.naive_bayes import MultinomialNB
clf = MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
clf = clf.fit(iris.data, iris.target)
y_predict=clf.predict(iris.data)
print('target=')
print(iris.target)
print('predict=')
print(y_predict)
print("多项分布朴素贝叶斯，样本总数： %d 错误样本数 : %d" % (iris.data.shape[0],(iris.target != y_predict).sum()))
输出为：
target=
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
predict=
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1
1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 1 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
多项分布朴素贝叶斯，样本总数： 150 错误样本数 : 7
- MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
参数作用
- alpha：浮点型可选参数，默认为1.0，其实就是添加拉普拉斯平滑，即为上述公式中的λ ，如果这个参数设置为0，就是不添加平滑；
- fit_prior：布尔型可选参数，默认为True。布尔参数fit_prior表示是否要考虑先验概率，如果是false,则所有的样本类别输出都有相同的类别先验概率。否则可以自己用第三个参数class_prior输入先验概率，或者不输入第三个参数class_prior让MultinomialNB自己从训练集样本来计算先验概率，此时的先验概率为P(Y=Ck)=mk/m。其中m为训练集样本总数量，mk为输出为第k类别的训练集样本数。
- class_prior：可选参数，默认为None。
对上述总结： 其中m为训练集样本总数量，mk为输出为第k类别的训练集样本数。
| fit_prior | class_prior | 最终先验概率P(Xi) |
|---|---|---|
| False | 填或不填没有意义 | P(Y = Ck) = 1 / k |
| True | 不填 | P(Y = Ck) = mk / m |
| True | 填 | P(Y = Ck) = class_prior |
3.伯努利分布朴素贝叶斯（BernoulliNB）
BernoulliNB 实现了用于多重伯努利分布数据的朴素贝叶斯训练和分类算法，即有多个特征，但每个特征 都假设是一个二元 (Bernoulli, boolean) 变量。 因此，这类算法要求样本以二元值特征向量表示；如果样本含有其他类型的数据， 一个BernoulliNB 实例会将其二值化(取决于 binarize 参数)。
伯努利分布朴素贝叶斯的决策规则基于：
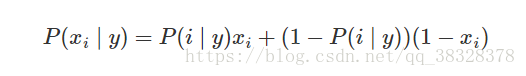
# 伯努利分布朴素贝叶斯
from sklearn import datasets
iris = datasets.load_iris()
from sklearn.naive_bayes import BernoulliNB
clf = BernoulliNB()
clf = clf.fit(iris.data, iris.target)
y_predict=clf.predict(iris.data)
print('target=')
print(iris.target)
print('predict=')
print(y_predict)
print("伯努利分布朴素贝叶斯，样本总数： %d 错误样本数 : %d" % (iris.data.shape[0],(iris.target != y_predict).sum()))
输出为：
target=
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
predict=
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0]
伯努利分布朴素贝叶斯，样本总数： 150 错误样本数 : 100
- 与多项分布朴素贝叶斯的规则不同。伯努利朴素贝叶斯明确地惩罚类 y 中没有出现作为预测因子的特征 i ，而多项分布分布朴素贝叶斯只是简单地忽略没出现的特征。
4.三种朴素贝叶斯的对比
与上述例子可知三种朴素贝叶斯的差别在：
| 朴素贝叶斯 | 样本总数 | 错误样本 |
|---|---|---|
| 高斯朴素贝叶斯 | 150 | 6 |
| 多项分布朴素贝叶斯 | 150 | 7 |
| 伯努利分布朴素贝叶斯 | 150 | 100 |
- 由上述表格可知高斯朴素贝叶斯准确率最高，也是我们朴素贝叶斯算法中最常用的。
三、朴素贝叶斯算法实现
该部分参考知乎：https://zhuanlan.zhihu.com/p/173945775
代码部分：
# 第一步，数据准备
from sklearn import datasets # 引入iris数据
import numpy as np
iris = datasets.load_iris()
X = iris.data[:,[2,3]]
y = iris.target
# print(iris.data)
print("Class labels:",np.unique(y)) # 打印分类类别的种类 [0 1 2]
# 第二步，切分训练数据和测试数据
from sklearn.model_selection import train_test_split
# 30%测试数据，70%训练数据，stratify=y表示训练数据和测试数据具有相同的类别比例
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=1,stratify=y) # 随机分配训练和测试数据集
# 第三步，数据标准化
from sklearn.preprocessing import StandardScaler
sc = StandardScaler() # 估算训练数据中的mu和sigma
sc.fit(X_train) # 使用训练数据中的mu和sigma对数据进行标准化
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
# 第四步，定制可视化函数：画出决策边界图(取2个特征才比较容易画出来)
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
def plot_decision_region(X,y,classifier,resolution=0.02):
markers = ('s','x','o','^','v')
colors = ('red','blue','lightgreen','gray','cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min,x1_max = X[:,0].min()-1,X[:,0].max()+1
x2_min,x2_max = X[:,1].min()-1,X[:,1].max()+1
xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),
np.arange(x2_min,x2_max,resolution))
Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1,xx2,Z,alpha=0.3,cmap=cmap)
plt.xlim(xx1.min(),xx1.max())
plt.ylim(xx2.min(),xx2.max())
# plot class samples
for idx,cl in enumerate(np.unique(y)):
plt.scatter(x=X[y==cl,0],
y = X[y==cl,1],
alpha=0.8,
c=colors[idx],
marker = markers[idx],
label=cl,
edgecolors='black')
# 第五步，朴素贝叶斯分类
from sklearn.naive_bayes import GaussianNB
from sklearn import metrics
gnb = GaussianNB()
gnb.fit(X_train_std,y_train) # 训练
res5 = gnb.predict(X_test_std) # 预测
print('predict=')
print(res5)
# print(sum(res5==y_train)) # 预测结果与真实结果比对
print(metrics.classification_report(y_test, res5, digits=4))# 准确率 召回率 F值 support
plot_decision_region(X_train_std,y_train,classifier=gnb,resolution=0.02)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
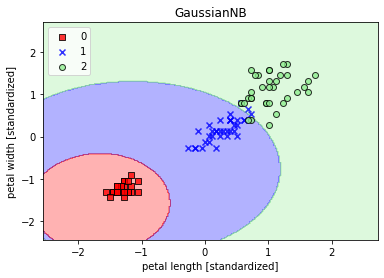
plt.title('GaussianNB')
plt.legend(loc='upper left')
plt.show()
输出结果如下：
- macro avg： 0.9792 0.9778 0.9778
Class labels: [0 1 2]
predict=
[2 0 0 1 1 1 2 1 2 0 0 2 0 1 0 1 2 1 1 2 2 0 1 2 1 1 1 2 0 2 0 0 1 1 2 2 0
0 0 1 2 2 1 0 0]
precision recall f1-score support
0 1.0000 1.0000 1.0000 15
1 0.9375 1.0000 0.9677 15
2 1.0000 0.9333 0.9655 15
accuracy 0.9778 45
macro avg 0.9792 0.9778 0.9778 45
weighted avg 0.9792 0.9778 0.9778 45
绘制的训练数据分类效果如下图所示，边界呈曲线分布。
总结
算法的优缺点
优点
- 逻辑清晰简单、易于实现，适合大规模数据。 根据算法的原理，只要我们把样本中所有属性相关的概率值都计算出来，然后分门别类地存储好，就获得了我们的朴素贝叶斯模型。
- 运算开销小。 根据上一条我们可以得知，所有预测需要用到的概率都已经准备好，当新数据来了之后，只需要获取对应的概率值，并进行简单的运算就能获得结果。
- 对于噪声点和无关属性比较健壮。 噪声点和无关属性对算法影响较小，在很多邮件服务中仍然一 直沿用这个方法进行垃圾邮件过滤。
- 预测过程快。 由于所有需要用到的属性相关概率都已经计算出来了，在新数据到来需要预测的时候，只需要把对应的一些概率值取出来进行计算就可以获得结果，所用到的时间和空间都很小。
缺点
由于做了 “各个属性之间是独立的” 这个假设，同样该算法也暴露了缺点。因为在实际应用中，属性之间
完全独立的情况是很少出现的，如果属性相关度较大，那么分类的效果就会变差。所以在具体应用的时
候要好好考虑特征之间的相互独立性，再决定是否要使用该算法，比如，维度太多的数据可能就不太适
合，因为在维度很多的情况下，不同的维度之间越有可能存在联合的情况，而不是相互独立的，那么模
型的效果就会变差。