[人工智能]PyTorch构建分类网络模型（Mnist数据集，全连接神经网络）

活动地址：CSDN21天学习挑战赛

项目数据及源码

可在github下载：

https://github.com/chenshunpeng/Pytorch-competitor-MNIST-dataset-classification

任务描述

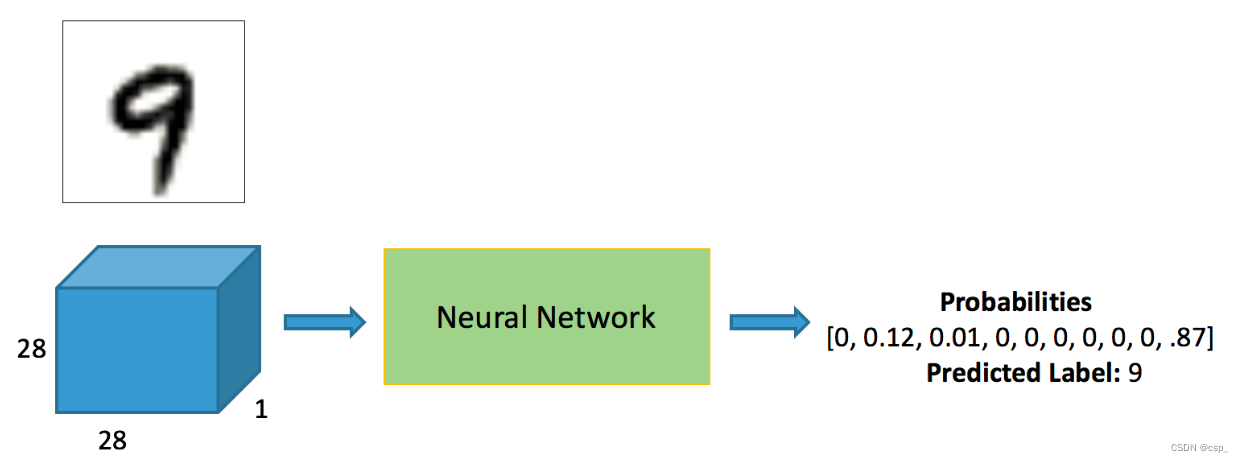
我们需要通过对手写数字数据集Mnist的训练，实现对于一个手写数字图像，判断其对应的数字值，判断方法是通过比较其和0~9这10个数字的相似程度，选出相似度最高的作为其识别的数字值，如下图，0~9这10个数字的相似程度最高的是9，为0.87，因此其识别结果为9

读取Mnist数据集

数据集地址：

http://yann.lecun.com/exdb/mnist/（也可在github项目中找到）

数据集介绍：

Dataset之MNIST：MNIST(手写数字图片识别+ubyte.gz文件)数据集简介、下载、使用方法(包括数据增强)之详细攻略

train-images-idx3-ubyte.gz:  training set images (9912422 bytes)
train-labels-idx1-ubyte.gz:  training set labels (28881 bytes)
t10k-images-idx3-ubyte.gz:   test set images (1648877 bytes)
t10k-labels-idx1-ubyte.gz:   test set labels (4542 bytes)

MNIST是一个非常有名的手写体数字识别数据集(手写数字灰度图像数据集)，在很多资料中，这个数据集都会被用作深度学习的入门样例

MNIST数据集是NIST数据集的一个子集，由0~9的数字图像构成的，每一张图片都有对应的标签数字，训练图像一共高60000张，供研究人员训练出合适的模型。测试图像一共高10000 张，供研究人员测试训练的模型的性能

其每张图片是包含28像素×28像素的灰度图像（1通道），各个像素的取值在0到255之间，每个图像数据都相应地标有数字标签

每张图片都由一个28×28的矩阵表示，且数字都会出现在图片的正中间，处理后的每一张图片是一个长度为784的一维数组（28*28=784），这个数组中的元素对应了图片像素矩阵中的每一个数字。

# 将matplotlib的图表直接嵌入到Notebook之中,或者使用指定的界面库显示图表

%matplotlib inline

from pathlib import Path
import requests

DATA_PATH = Path("data")
PATH = DATA_PATH / "mnist"

PATH.mkdir(parents=True, exist_ok=True)

FILENAME = "mnist.pkl.gz"

import pickle
import gzip

with gzip.open((PATH / FILENAME).as_posix(), "rb") as f:
    ((x_train, y_train), (x_valid, y_valid),
     _) = pickle.load(f, encoding="latin-1")

查看数据集信息：

from matplotlib import pyplot
import numpy as np

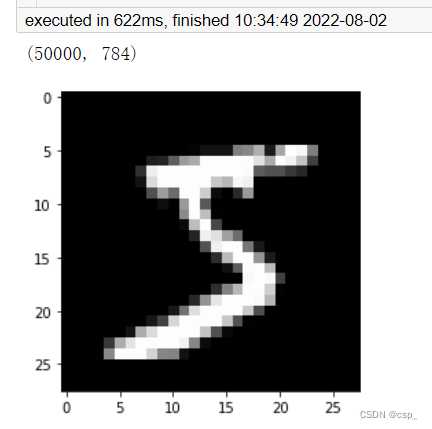
pyplot.imshow(x_train[0].reshape((28, 28)), cmap="gray")
print(x_train.shape)
# 50000个样本，每个图像是28*28*1

我们可以通过x_train[0]看到这个数字的矩阵表示，但是由于无法按照28×28显示，看不出来其是 5 的轮廓，矩阵表示如下：

tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0117,
        0.0703, 0.0703, 0.0703, 0.4922, 0.5312, 0.6836, 0.1016, 0.6484, 0.9961,
        0.9648, 0.4961, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1172, 0.1406, 0.3672, 0.6016,
        0.6641, 0.9883, 0.9883, 0.9883, 0.9883, 0.9883, 0.8789, 0.6719, 0.9883,
        0.9453, 0.7617, 0.2500, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1914, 0.9297, 0.9883, 0.9883,
        0.9883, 0.9883, 0.9883, 0.9883, 0.9883, 0.9883, 0.9805, 0.3633, 0.3203,
        0.3203, 0.2188, 0.1523, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0703, 0.8555, 0.9883,
        0.9883, 0.9883, 0.9883, 0.9883, 0.7734, 0.7109, 0.9648, 0.9414, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.3125,
        0.6094, 0.4180, 0.9883, 0.9883, 0.8008, 0.0430, 0.0000, 0.1680, 0.6016,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0547, 0.0039, 0.6016, 0.9883, 0.3516, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.5430, 0.9883, 0.7422, 0.0078, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0430, 0.7422, 0.9883, 0.2734,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1367, 0.9414,
        0.8789, 0.6250, 0.4219, 0.0039, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.3164, 0.9375, 0.9883, 0.9883, 0.4648, 0.0977, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.1758, 0.7266, 0.9883, 0.9883, 0.5859, 0.1055, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0625, 0.3633, 0.9844, 0.9883, 0.7305,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.9727, 0.9883,
        0.9727, 0.2500, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1797, 0.5078, 0.7148, 0.9883,
        0.9883, 0.8086, 0.0078, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.1523, 0.5781, 0.8945, 0.9883, 0.9883,
        0.9883, 0.9766, 0.7109, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0938, 0.4453, 0.8633, 0.9883, 0.9883, 0.9883,
        0.9883, 0.7852, 0.3047, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0898, 0.2578, 0.8320, 0.9883, 0.9883, 0.9883, 0.9883,
        0.7734, 0.3164, 0.0078, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0703, 0.6680, 0.8555, 0.9883, 0.9883, 0.9883, 0.9883, 0.7617,
        0.3125, 0.0352, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.2148, 0.6719, 0.8828, 0.9883, 0.9883, 0.9883, 0.9883, 0.9531, 0.5195,
        0.0430, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.5312, 0.9883, 0.9883, 0.9883, 0.8281, 0.5273, 0.5156, 0.0625,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
        0.0000])

将数据需转换成tensor：

import torch

x_train, y_train, x_valid, y_valid = map(torch.tensor,
                                         (x_train, y_train, x_valid, y_valid))
n, c = x_train.shape
x_train, x_train.shape, y_train.min(), y_train.max()
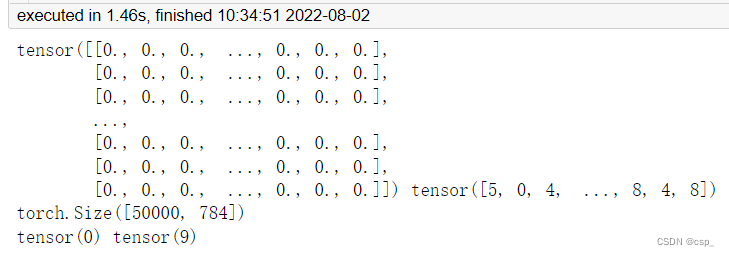
print(x_train, y_train)
print(x_train.shape)
print(y_train.min(), y_train.max())

结果：

设计全连接神经网络

全连接网络中，要求输入的是一个矩阵，因此需要将1x28x28的这个三阶的张量变成一个一阶的向量，因此将图像的每一行的向量横着拼起来变成一串，这样就变成了一个维度为1x784的向量，一共输入N个手写数图，因此，输入矩阵维度为（N，784），这样就可以设计我们的模型，如下图所示

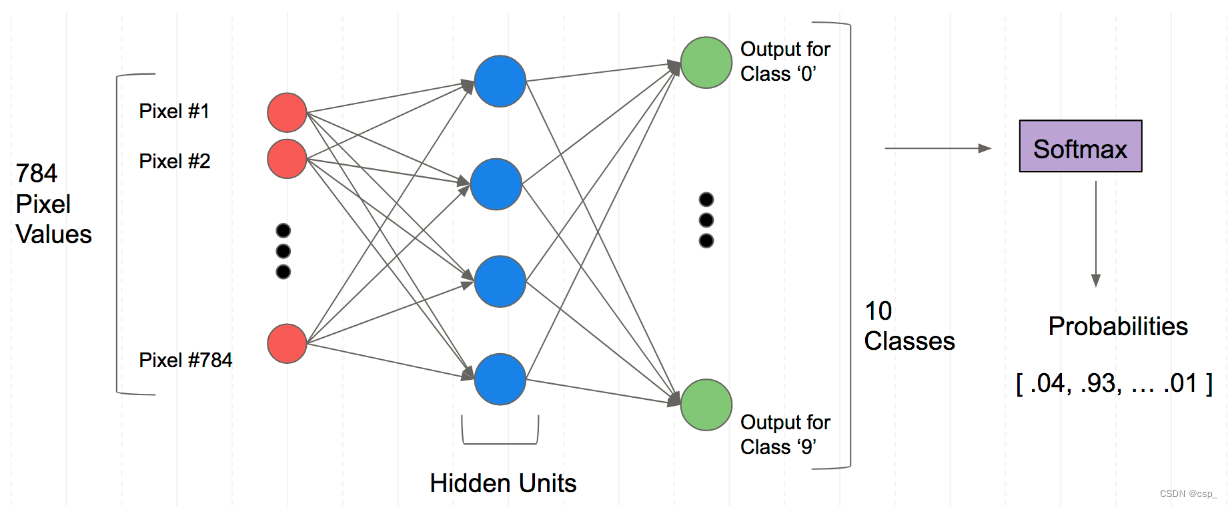
构造Mnist_NN类，定义函数

需要注意：

• Mnist_NN类必须继承nn.Module且在其构造函数中需调用nn.Module的构造函数
• 无需写反向传播函数，nn.Module能够利用autograd自动实现反向传播
• Module中的可学习参数可以通过named_parameters()或者parameters()返回迭代器

from torch import nn
from torch import optim
import torch.nn.functional as F
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
import numpy as np


# 继承nn.Module
class Mnist_NN(nn.Module):
    # 构造函数
    def __init__(self):
        # 调用nn.Module的构造函数
        super().__init__()
        self.hidden1 = nn.Linear(784, 128) # 隐层1
        self.hidden2 = nn.Linear(128, 256) # 隐层2
        self.out = nn.Linear(256, 10) # 输出层

    # 前向传播
    def forward(self, x):
        # import torch.nn.functional as F
        x = F.relu(self.hidden1(x))
        x = F.relu(self.hidden2(x))
        x = self.out(x)
        return x

创建Mnist_NN类对象net并查看信息：

net = Mnist_NN()
print(net)

输出：

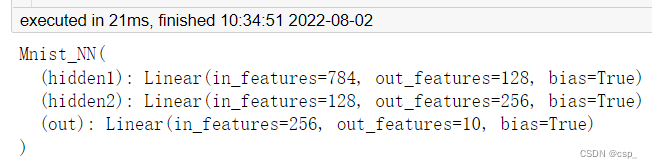
可以打印我们定义好名字里的权重和偏置项：

for name, parameter in net.named_parameters():
    print(name, parameter, parameter.size())

结果：

hidden1.weight Parameter containing:
tensor([[-0.0107,  0.0176,  0.0235,  ...,  0.0040, -0.0234,  0.0087],
        [ 0.0177, -0.0273,  0.0112,  ..., -0.0134,  0.0282, -0.0013],
        [ 0.0139, -0.0125,  0.0143,  ..., -0.0239,  0.0263, -0.0089],
        ...,
        [-0.0204,  0.0160,  0.0061,  ..., -0.0239, -0.0082, -0.0247],
        [ 0.0070, -0.0266, -0.0093,  ..., -0.0144,  0.0022,  0.0010],
        [ 0.0227,  0.0055,  0.0275,  ..., -0.0272,  0.0136, -0.0164]],
       requires_grad=True) torch.Size([128, 784])
hidden1.bias Parameter containing:
tensor([-0.0097,  0.0237,  0.0018, -0.0330, -0.0280, -0.0191, -0.0255,  0.0288,
         0.0225,  0.0101, -0.0063, -0.0276,  0.0091,  0.0075, -0.0313,  0.0057,
        -0.0356, -0.0265,  0.0286, -0.0057, -0.0100, -0.0276,  0.0178, -0.0170,
        -0.0174,  0.0337,  0.0259, -0.0143,  0.0314,  0.0331,  0.0341,  0.0189,
        -0.0315, -0.0170,  0.0237,  0.0156, -0.0345,  0.0154,  0.0197,  0.0305,
         0.0349, -0.0326,  0.0193, -0.0336,  0.0142,  0.0262,  0.0215,  0.0004,
         0.0243,  0.0236, -0.0195, -0.0208,  0.0333, -0.0104,  0.0033,  0.0118,
         0.0113, -0.0340,  0.0155,  0.0261, -0.0089,  0.0287, -0.0242,  0.0022,
        -0.0165, -0.0296,  0.0008,  0.0316, -0.0224, -0.0037,  0.0105,  0.0057,
         0.0285, -0.0158, -0.0013, -0.0340,  0.0287, -0.0043, -0.0148, -0.0273,
        -0.0066,  0.0082, -0.0170, -0.0021, -0.0280,  0.0211, -0.0165, -0.0103,
         0.0152, -0.0128, -0.0211, -0.0180, -0.0097,  0.0089,  0.0338,  0.0322,
        -0.0210, -0.0235, -0.0123, -0.0219, -0.0201,  0.0003, -0.0106, -0.0303,
        -0.0003, -0.0157,  0.0188,  0.0179,  0.0237, -0.0351, -0.0146, -0.0205,
        -0.0284,  0.0218,  0.0107, -0.0353,  0.0253, -0.0196, -0.0317, -0.0294,
         0.0184,  0.0201,  0.0059,  0.0260,  0.0134, -0.0217,  0.0091, -0.0089],
       requires_grad=True) torch.Size([128])
hidden2.weight Parameter containing:
tensor([[-0.0658,  0.0262,  0.0356,  ...,  0.0520, -0.0872,  0.0459],
        [-0.0443, -0.0812, -0.0046,  ...,  0.0819, -0.0386, -0.0344],
        [-0.0703,  0.0753, -0.0350,  ..., -0.0035,  0.0188,  0.0194],
        ...,
        [ 0.0556,  0.0688, -0.0311,  ..., -0.0033,  0.0832, -0.0497],
        [ 0.0164,  0.0710,  0.0368,  ...,  0.0303,  0.0231,  0.0512],
        [-0.0437,  0.0875,  0.0315,  ...,  0.0002,  0.0679, -0.0412]],
       requires_grad=True) torch.Size([256, 128])
hidden2.bias Parameter containing:
tensor([ 7.7913e-03, -5.2409e-02,  3.7981e-02,  6.4097e-02,  6.5983e-02,
        -1.2665e-02, -5.3630e-02,  1.8194e-02,  2.8534e-02,  8.3733e-02,
         5.3927e-02,  2.3522e-02, -2.2915e-02,  7.9818e-02, -4.8618e-02,
        -4.9321e-02, -6.4636e-02,  4.5667e-02,  6.2186e-02,  2.9977e-02,
        -3.8158e-02,  6.4900e-02, -5.5211e-02, -4.5465e-02, -7.5447e-02,
        -1.3676e-03,  1.8499e-02,  2.6505e-02, -1.3459e-02,  6.3754e-02,
        -3.7523e-02,  5.7949e-02, -5.9734e-02, -8.6329e-02,  2.9193e-02,
         2.0645e-02,  2.8751e-02,  6.2095e-02,  6.5391e-02, -1.3178e-02,
         5.2374e-02, -5.1765e-02, -5.7692e-02, -4.6615e-02, -1.6571e-02,
        -6.7677e-02, -6.8337e-02, -4.4569e-02, -1.3499e-02, -7.0806e-02,
         1.7268e-02,  7.9308e-02, -9.2949e-03,  8.3358e-02, -2.8339e-03,
         3.6183e-02, -3.0781e-03, -7.8056e-02, -2.5781e-02, -6.1548e-02,
        -4.2550e-03,  8.4365e-02,  7.6643e-02,  2.6072e-03,  3.8844e-02,
        -9.1026e-03,  1.7072e-02,  1.5069e-02, -1.5344e-02, -7.1375e-02,
        -2.4087e-02,  4.8563e-02,  4.3171e-02,  3.7335e-02,  3.9004e-02,
         4.7122e-02,  6.3475e-02,  4.2615e-02, -6.1060e-02,  1.4865e-02,
         4.5167e-02, -8.0974e-02,  5.3717e-03, -3.9014e-02,  8.3588e-02,
         6.5867e-02, -3.4913e-02,  5.8872e-02,  6.7077e-02, -6.3365e-02,
         8.6366e-02,  3.5593e-02,  4.6238e-02,  8.3289e-02, -1.4793e-02,
         7.2298e-02,  6.0482e-02,  4.2920e-02,  3.9899e-02,  8.2298e-02,
         4.3614e-02,  8.3762e-03,  6.7424e-02, -5.9824e-02, -5.2346e-02,
         5.3317e-02, -1.8010e-02,  7.9718e-03,  4.9618e-02,  5.7588e-03,
         2.6586e-02,  4.7773e-02, -7.4746e-02, -4.2066e-03,  6.3242e-02,
        -8.4219e-03, -7.7916e-02, -7.9803e-02,  1.4334e-02,  5.2814e-02,
        -7.5703e-02,  8.8523e-03,  6.0214e-03,  5.8813e-02,  4.3685e-02,
         3.1810e-03,  5.6022e-02, -6.4101e-02, -6.3819e-02, -8.0192e-02,
         2.3717e-02,  9.3828e-03, -2.4051e-02, -1.5994e-02, -6.8268e-02,
        -8.3660e-02, -7.3033e-02, -6.6568e-02,  3.7064e-02, -3.3497e-02,
        -8.7144e-02,  8.3359e-02, -1.3661e-02,  3.5242e-02,  3.0770e-02,
        -2.1677e-02, -7.5600e-02, -2.8537e-02, -1.9357e-02, -5.9502e-02,
         7.9158e-02, -2.8801e-02, -2.2144e-02,  8.5924e-04,  7.5870e-02,
         6.6614e-02,  1.4565e-02, -5.7472e-02,  8.0418e-02,  6.6934e-02,
         3.2934e-02,  5.2901e-03, -7.0742e-03,  4.2174e-02,  5.4780e-02,
        -6.9979e-02,  5.7612e-02,  4.3069e-02, -1.9059e-02,  5.2661e-02,
         3.0751e-02, -5.5104e-02, -5.3951e-02,  9.0439e-03, -2.0585e-02,
         2.0851e-02, -3.0479e-02,  4.0783e-03,  2.2134e-02,  6.5000e-02,
         8.0417e-02, -4.5733e-02,  3.5371e-02,  2.2602e-02,  3.9445e-02,
         5.0051e-02,  1.1277e-02,  8.4714e-03, -3.4974e-02,  1.4301e-02,
         5.3342e-02,  2.7742e-02, -8.6245e-02,  4.0869e-02, -8.0224e-02,
        -3.9399e-02,  8.7867e-02,  5.3911e-02,  4.4785e-02, -8.7924e-02,
         5.3280e-02,  5.5927e-02,  3.0065e-02,  4.8404e-02,  5.4177e-02,
        -6.6974e-02,  3.5416e-02,  8.9249e-03,  7.0158e-02,  2.6166e-02,
         6.6212e-04,  8.5239e-02,  3.1147e-02,  2.9362e-02,  8.2084e-02,
        -8.0664e-02, -3.9999e-02,  4.9067e-02,  6.4668e-02, -6.9497e-02,
        -4.6120e-02,  3.0965e-02, -5.0559e-02,  4.8063e-02, -6.1079e-02,
         4.0454e-02,  7.1121e-02,  6.7732e-02,  1.7263e-02,  3.8927e-02,
         3.4393e-02,  2.5543e-02, -7.6177e-02,  1.5727e-02, -3.0954e-02,
         6.5176e-02,  8.5865e-03,  4.0888e-02, -7.4767e-05,  6.3285e-02,
         2.6874e-02, -4.7549e-02, -2.6836e-02, -5.2410e-02, -4.1517e-02,
        -6.4450e-03, -5.6177e-02,  3.9314e-02, -5.7746e-02,  4.6241e-02,
        -7.3782e-02,  8.7160e-02,  8.6259e-02,  8.5354e-02, -2.9345e-02,
         1.3077e-02], requires_grad=True) torch.Size([256])
out.weight Parameter containing:
tensor([[-0.0613, -0.0281, -0.0492,  ...,  0.0526,  0.0189, -0.0455],
        [-0.0086, -0.0281, -0.0385,  ..., -0.0198, -0.0447, -0.0342],
        [ 0.0407,  0.0162, -0.0182,  ...,  0.0353, -0.0350,  0.0405],
        ...,
        [ 0.0398,  0.0623, -0.0503,  ...,  0.0261, -0.0479, -0.0239],
        [-0.0221, -0.0278,  0.0564,  ...,  0.0249, -0.0339, -0.0200],
        [ 0.0242, -0.0149,  0.0027,  ..., -0.0408,  0.0173, -0.0111]],
       requires_grad=True) torch.Size([10, 256])
out.bias Parameter containing:
tensor([-0.0526,  0.0188,  0.0049, -0.0456, -0.0164, -0.0436,  0.0448,  0.0018,
        -0.0373, -0.0142], requires_grad=True) torch.Size([10])

使用TensorDataset和DataLoader来简化数据处理：

get_data()函数：

shuffle即是否对数据集进行洗牌操作，默认设置为False（数据类型 bool）

将输入数据的顺序打乱，是为了使数据更有独立性，但如果数据是有序列特征的，就不要设置成True了

一般对训练集进行shuffle操作而对测试集保留原有的顺序结构（原始数据在样本均衡的情况下可能是按照某种顺序进行排列，如前半部分为某一类别的数据，后半部分为另一类别的数据，打乱之后数据的排列就会拥有一定的随机性，减小模型抖动）

def get_data(train_ds, valid_ds, bs):
    return (
        DataLoader(train_ds, batch_size=bs, shuffle=True),
        DataLoader(valid_ds, batch_size=bs * 2),
    )

get_model()函数：

在 PyTorch的torch.optim包中提供了非常多的可实现参数自动优化的类，如 SGD 、AdaGrad 、RMSProp 、Adam等优化算法，这些类都可以被直接调用

本次实验使用了最基本的优化算法SGD

def get_model():
    model = Mnist_NN()
    return model, optim.SGD(model.parameters(), lr=0.001)

loss_batch()函数：

def loss_batch(model, loss_func, xb, yb, opt=None):
    loss = loss_func(model(xb), yb)

    if opt is not None:
        loss.backward()
        opt.step()
        opt.zero_grad()

    return loss.item(), len(xb)

fit()函数：

• 一般在训练模型时加上model.train()，这样会正常使用Batch Normalization和 Dropout
• 测试的时候一般选择model.eval()，这样就不会使用Batch Normalization和 Dropout，将测试集的数据送入神经网络模型进行训练，计算模型在测试集上的综合表现能力

def fit(steps, model, loss_func, opt, train_dl, valid_dl):
    for step in range(steps):
        model.train()
        for xb, yb in train_dl:
            loss_batch(model, loss_func, xb, yb, opt)

        model.eval()
        with torch.no_grad():
            losses, nums = zip(
                *[loss_batch(model, loss_func, xb, yb) for xb, yb in valid_dl])
        val_loss = np.sum(np.multiply(losses, nums)) / np.sum(nums)
        print('当前step:' + str(step), '验证集损失：' + str(val_loss))

进行训练

bs即batch_size（数据类型 int），在进行深度学习处理时，常常将数据集划分为一个个的批次，每个批次有固定的数据数目，在此就是指定一个批次的数据量

train_ds = TensorDataset(x_train, y_train)
valid_ds = TensorDataset(x_valid, y_valid)
bs = 64
train_dl, valid_dl = get_data(train_ds, valid_ds, bs)
model, opt = get_model()
loss_func = F.cross_entropy # 交叉熵损失函数
fit(25, model, loss_func, opt, train_dl, valid_dl)

结果：

当前step:0 验证集损失：2.2809557510375975
当前step:1 验证集损失：2.2500623081207274
当前step:2 验证集损失：2.202859774017334
当前step:3 验证集损失：2.123643782043457
当前step:4 验证集损失：1.9911612365722657
当前step:5 验证集损失：1.7912375587463378
当前step:6 验证集损失：1.5452837438583373
当前step:7 验证集损失：1.3032891147613526
当前step:8 验证集损失：1.1027766933441163
当前step:9 验证集损失：0.949706922531128
当前step:10 验证集损失：0.8340907591819763
当前step:11 验证集损失：0.7464724873542785
当前step:12 验证集损失：0.6767623687744141
当前step:13 验证集损失：0.622122283744812
当前step:14 验证集损失：0.5775999296188354
当前step:15 验证集损失：0.5417200242042541
当前step:16 验证集损失：0.5122299160003662
当前step:17 验证集损失：0.4875089702606201
当前step:18 验证集损失：0.46718254098892215
当前step:19 验证集损失：0.4494625943660736
当前step:20 验证集损失：0.4347919206619263
当前step:21 验证集损失：0.4215654832363129
当前step:22 验证集损失：0.41056136293411255
当前step:23 验证集损失：0.4001917915582657
当前step:24 验证集损失：0.39120743613243103

预测结果可视化

predicted = model(x_train[:]).data.numpy()
res=np.argmax(predicted, axis=1)

import matplotlib.pyplot as plt

fig=plt.figure()
plt.figure(figsize=(12,5))

for i in range(30):
    plt.subplot(5,6,i+1)
    plt.tight_layout()
    plt.imshow(x_train[i].reshape((28, 28)), cmap="gray")
    plt.title("True value: {}\npredictive value: {}".format(y_train[i],res[i])) 
    plt.xticks([]) 
    plt.yticks([])

结果：