多视图多实例多标签主动学习
主动学习
主动学习(Active Learning)的大致思路就是:通过机器学习的方法获取到那些比较 “难” 分类的样本数据,让人工再次确认和审核,然后将人工标注得到的数据再次使用有监督学习模型或者半监督学习模型进行训练,逐步提升模型的效果,将人工经验融入机器学习的模型中。
多示例多标签学习
传统的监督学习中,一个图像区域以一个instance(示例)呈现,并仅关联于一个标签。很多图像多标签标注的方法是通过将图像进行物体分割或物体检测,然后对每个区域的物体进行标注。而多示例多标签学习方法省去了检测/分割部分工作。
多示例多视图学习
单视图多示例主动学习主要关注同一视图内包之间的内部关系。相比之下,多视图多示例主动学习应该考虑跨视图的包之间的相互关系。由于特征视图的异构性,所选的包标签对在视图之间可能不一致。由于每个视图表示来自不同视角的对象,因此从单个视图导出的包标签对不可靠。因此,多视图数据的个性和共性信息都应该考虑到多视图数据的主动学习。
M3AL
M3AL首先学学习了跨多个视图的包的共享信息和特有信息;然后量化每个未标记包在多个视图中的实例分布,以测试包的多样性。然后训练初始的包预测器;然后通过组合包的共享信息和特有信息及其不同的实例分布来计算整体不确定性; 最后使用组合的不确定性来选择信息最丰富的包标签对进行查询;用获得的查询响应更新标签相关矩阵和包预测器。
符号系统
| 符号 | 含义 |
|---|---|
| D l v = { ( X 1 v , Y 1 ) , ( X 2 v , Y 2 ) , ? ? , ( X l v , Y l ) } \mathcal{D}_l^v=\{(\mathcal{X_1^v},\mathbf{Y}_1),(\mathcal{X_2^v},\mathbf{Y}_2),\cdots,(\mathcal{X_l^v},\mathbf{Y}_l)\} Dlv?={(X1v?,Y1?),(X2v?,Y2?),?,(Xlv?,Yl?)} | 第 v v v个视图中的 l l l个有标记的包 |
| m i v m_i^v miv? | 第 v v v个视图中第 i i i个包中的实例个数 |
| x v \mathbf{x}^v xv | 第 v v v个视图中实例的特征空间 |
| S \mathbf{S} S | 不同视图间的共享信息 |
| P \mathbf{P} P | 不同视图间的特有信息 |
| U ( S ^ , i , c ) U(\widehat{\mathbf{S}},i,c) U(S ,i,c) | 在多个视图下包标签对 < i , c > <i,c> <i,c>的共享信息 |
| U ( P ^ v , i , c ) U(\widehat{\mathbf{P}}^v,i,c) U(P v,i,c) | 在 v v v视图下包标签对 < i , c > <i,c> <i,c>的特有信息 |
开局一张图
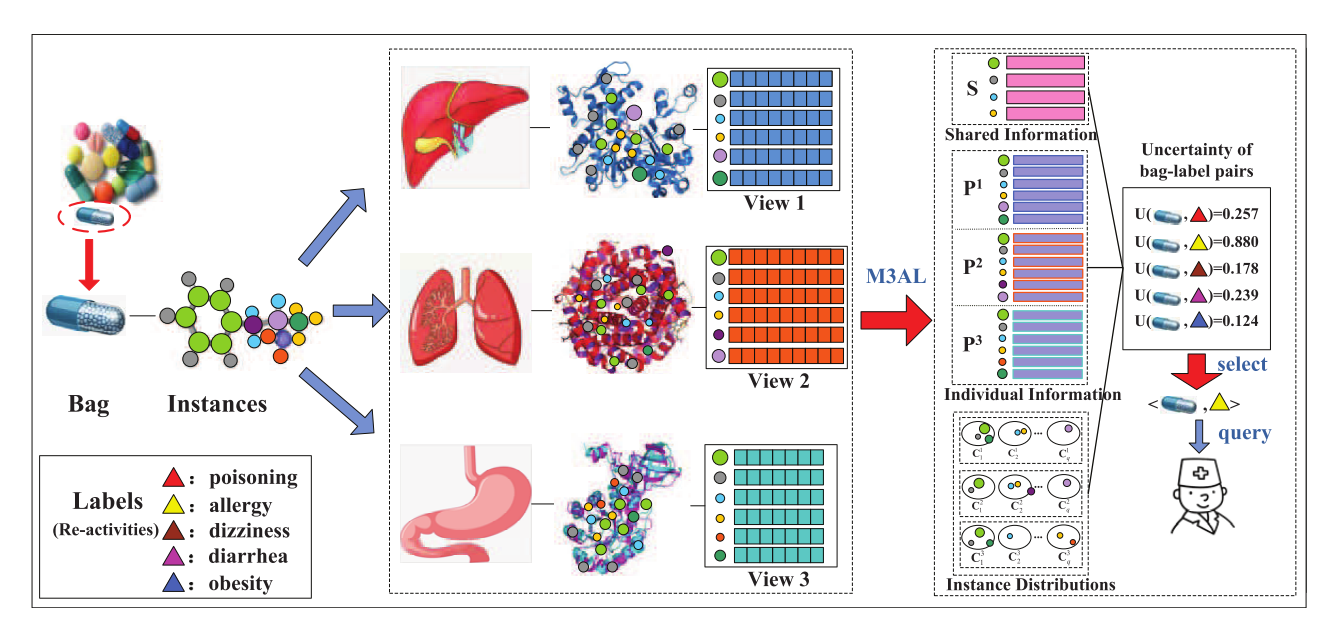
一种药物被视作一个包,一种药物由多种化合物组成,这些化合物被视作包中实例。药物在不同器官中的表示被视作不同的视图。 S \mathbf{S} S表示不同视图之间的共享信息, P \mathbf{P} P表示不同视图特有信息。考虑到这些器官的 S \mathbf{S} S和 P \mathbf{P} P,待验证的药物反应对不仅应关注不同器官共有的那些,还应关注个别器官特有的对。这些包-标签对可以优先交给生物医学专家进行定向调查。
提取多视图包的个性和共性:
Θ
(
{
P
v
=
1
v
}
,
S
)
=
min
?
1
V
∑
v
=
1
V
∣
∣
X
v
?
(
S
+
P
v
)
X
v
∣
∣
F
2
+
λ
1
Φ
1
(
S
)
(
{
P
v
}
v
=
1
V
)
+
λ
2
Φ
2
(
S
)
\Theta(\{\mathbf{P}^v_{v=1}\},\mathbf{S})=\min \frac{1}{V}\sum\limits_{v=1}^V||\mathbf{X}^v-(\mathbf{S}+\mathbf{P}^v)\mathbf{X}^v ||_F^2+\lambda_1\Phi_1(\mathbf{S})(\{\mathbf{P}^v\}^V_{v=1})+\lambda_2\Phi_2(\mathbf{S})
Θ({Pv=1v?},S)=minV1?v=1∑V?∣∣Xv?(S+Pv)Xv∣∣F2?+λ1?Φ1?(S)({Pv}v=1V?)+λ2?Φ2?(S)
首先使用别的多示例文章的处理标准将包 X i v \mathcal{X}_i^v Xiv?转换为单向量表示 X i v \mathbf{X}_i^v Xiv?,第一项时跨视图获取包的共享信息和个体特征信息,第二项用于加强不同视图下编码矩阵之间的差异 { P v } v = 1 V \{\mathbf{P}^v\}^V_{v=1} {Pv}v=1V?,第三项是追求跨视图的共性编码矩阵 S \mathbf{S} S.
包的多样性计算:
D
B
v
(
i
)
=
1
C
∑
c
=
1
C
β
c
v
(
i
)
l
o
g
(
β
c
v
(
i
)
)
+
(
1
?
β
c
v
(
i
)
)
l
o
g
(
1
?
β
c
v
(
i
)
)
l
o
g
(
0.5
)
DB^v(i)=\frac{1}{C}\sum\limits_{c=1}^C\frac{\beta_c^v(i)log(\beta_c^v(i))+(1-\beta_c^v(i))log(1-\beta_c^v(i))}{log(0.5)}
DBv(i)=C1?c=1∑C?log(0.5)βcv?(i)log(βcv?(i))+(1?βcv?(i))log(1?βcv?(i))?
D
B
(
i
)
=
1
V
∑
v
=
1
V
D
B
v
(
i
)
DB(i)=\frac{1}{V}\sum\limits_{v=1}^{V}DB^v(i)
DB(i)=V1?v=1∑V?DBv(i)
如果包的所有实例具有不相同的分布或标签,则该包的多样性较高,更可能被选择用于查询。查询具有不同实例分布的包可以大大降低模型的不确定性。
伪代码
