开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 循环神经网络（RNN） -> 正文阅读

[人工智能]循环神经网络（RNN）

循环神经网络

RNN

0 为什么需要RNN？？

RNN对具有序列特性的数据非常有效，它能挖掘数据中的时序信息以及语义信息。

利用了RNN的这种能力，使深度学习模型在解决语音识别、语言模型、机器翻译以及时序分析等NLP领域的问题时有所突破。

0.1 例子：为什么需要时序信息？

第一句话：I like eating apple！（我喜欢吃苹果！）
第二句话：The Apple is a great company！（苹果真是一家很棒的公司！）

现在的任务是要给apple打Label，我们都知道第一个apple是一种水果，第二个apple是苹果公司。

假设我们现在有大量的已经标记好的数据以供训练模型，当我们使用全连接的神经网络时，我们做法是把apple这个单词的特征向量输入到我们的模型中，在输出结果时，让我们的label里把概率最大的label当作正确的label。

但我们的语料库中，有的apple的label是水果，有的label是公司，这将导致模型在训练的过程中，预测的准确程度取决于训练集中哪个label多一些，这样的模型对于我们来说完全没有作用。

问题就出在了我们没有结合上下文去训练模型，而是单独的在训练apple这个单词的label，这也是全连接神经网络模型所不能做到的，于是就有了我们的循环神经网络。

1. 关于RNN的神经网络

1.1 结构图

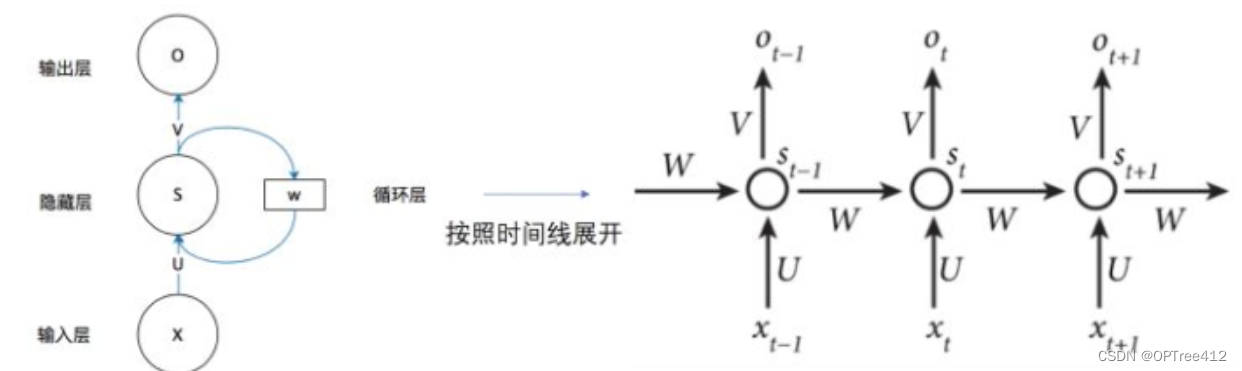
模型结构图
其中，xt是t时刻的输入值，ht是t时刻的隐藏层的值，yt是t时刻的输出层的值。U，V，W分别是输入，隐藏层，输出的权重矩阵。

从图上的参数（U，V，W）的下标不变可以看出，RNN的参数是共享的。专业一点说就是，在同一层隐藏层中，不同时刻的U，V，W均是相等地，这也就是RNN的参数共享。

另外，xt可以看出输入时候时间顺序的，因此这也注定了RNN无法做到并行运算来提高速度。

从结构图中我们可以发现ht并不单单只是由Xt决定，还与t-1时刻的隐藏层的值ht-1有关。从这个隐藏层的ht就不难看出，所谓的隐藏层的循环操作就是每一时刻计算一个隐藏层地值，然后再把该隐藏层地值传入到下一时刻，达到信息传递的目的。由此我们再看看数学公式。

2. RNN详细分析

2. 1 RNN具体公式

RNN具体公式如下
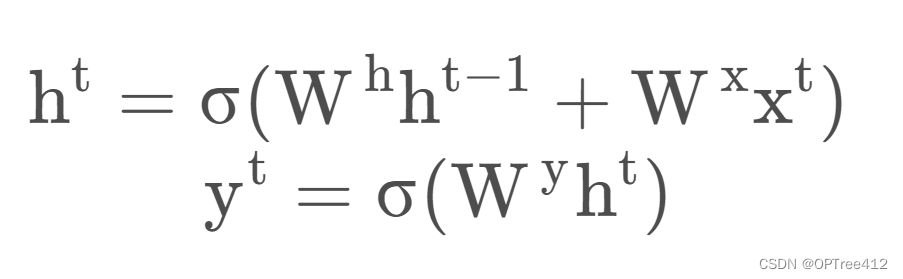
RNN的公式
我们可以看到ht与t-1时刻输入的记忆和这次的输入xt有关。这就是公式层面来表达为什么RNN具有“记忆”了。

对于RNN，对于某个序列，对于时刻t，它的词向量输出概率为P(x_t | x₁,x₂,…,x_t-1)，则softmax层每个神经元的计算如下：
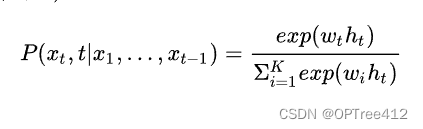
在这里插入图片描述
其中h_t是当前第t个位置的隐含状态，它与上一时刻的状态及当前输入有关，即h_t=f(h_t-1,x_t)，t表示文本词典中的第t个词对应的下标。x_t表示词典中第t个词；w_t是词权重参数。
那么整个序列的生成概率就为
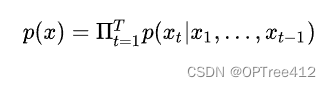
在这里插入图片描述

2. 2 RNN要这么多yt干嘛？

从上面的公式讲解来看，在每个时间步都有输出，但根据任务，这可能不是必需的。

例如，在预测句子的情绪时，我们可能只关心最终的输出，而不是每个单词之后的情绪。同样，我们可能不需要在每个时间步骤输入。所以，RNN结构可以是下列不同的组合：
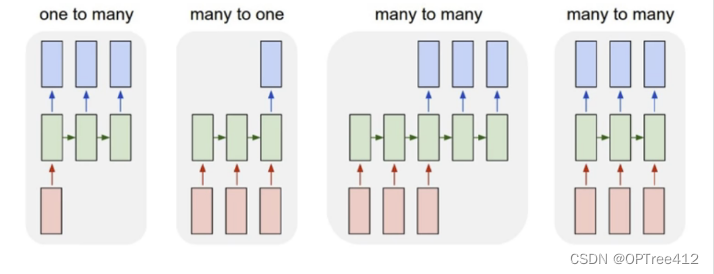
在这里插入图片描述
one - to - n（左一）：
输入的是一个独立数据，需要输出一个序列数据，常见的任务类型有：
1.基于图像生成文字描述
2.基于类别生成一段语言，文字描述

n - to - one（左二）：
输入一段序列，最后输出一个概率，通常用来处理序列分类问题，常见任务：
1.文本情感分析
2.文本分类

n - to - n（右二）：
最为经典地RNN任务，输入和输出都是等长地序列，常见的任务有：
1.计算视频中每一帧的分类标签
2.输入一句话，判断一句话中每个词的词性

n - to - m（右一）：
输入序列和输出序列不等长地任务,也就是Encoder-Decoder结构，这种结构有非常多的用法：
1.机器翻译：Encoder-Decoder的最经典应用，事实上这结构就是在机器翻译领域最先提出的
2.文本摘要：输入是一段文本序列，输出是这段文本序列的摘要序列
3.阅读理解：将输入的文章和问题分别编码，再对其进行解码得到问题的答案
4.语音识别：输入是语音信号序列，输出是文字序列

2.3 RNN的梯度问题

2.3.1 RNN的梯度消失？

RNN的梯度消失并不是真的突然就消失了，而是RNN中对较远时间步的梯度消失了。

下图是帮助你更好的理解他所谓的RNN中对较远时间步的梯度消失了是怎办么一回事。其中不同的颜色就是表示不同时期的记忆，从这里可以看出以前的记忆越来越“淡了”。
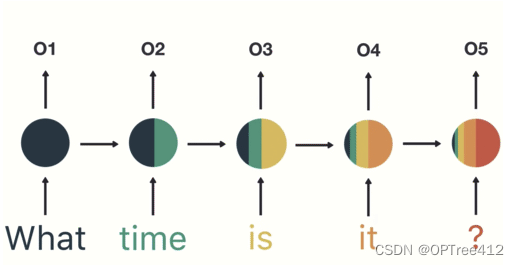
在这里插入图片描述

下面开始是纯数学推导了，谨慎观看

RNN中反向传播使用的是back propagation through time(BPTT)方法。这里假设我们的时间序列只有三段，在t=3时刻，损失函数为：
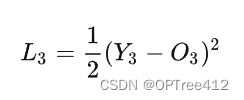
在这里插入图片描述
则对于一次训练任务的损失函数为下图公式，即每一时刻损失值的累加。

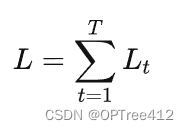
使用随机梯度下降法训练RNN其实就是对Wx、Ws、Wo求偏导，并不断调整它们以使L尽可能达到最小的过程。(注意此处把上文中的U、W、V参数相应替换为Wx、Ws、Wo，分别是输入，隐藏层，输出的权重矩阵，以保持和引用的文章一致。)

现在假设我们的时间序列只有三段，t1，t2，t3。我们只对t3时刻的Wx、Ws、Wo求偏导（其他时刻类似）：
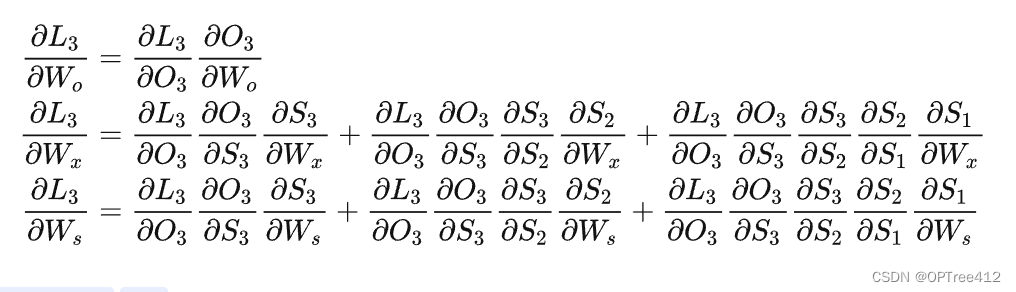
在这里插入图片描述

可以看出损失函数对于Wo（输出权重）并没有长期依赖，但是因为st着时间序列向前传播，而st（隐藏值）又是Wx（输入权重）、Ws（隐藏层权重）的函数，所以对于Wx、Ws会随着时间序列产生长期依赖。

根据上述求偏导的过程，我们可以得出任意时刻对Wx、Ws求偏导的公式，任意时刻对Ws求偏导的公式同上。
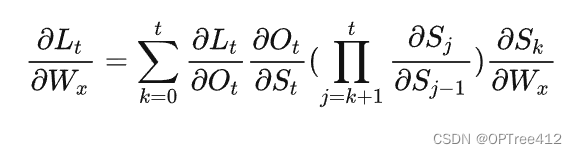
在这里插入图片描述

如果加上激活函数（tanh）
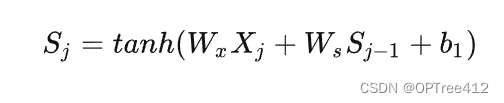
在这里插入图片描述
激活函数tanh的定义如下：

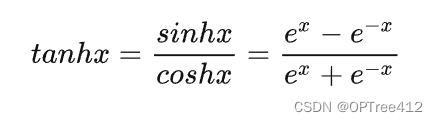
则
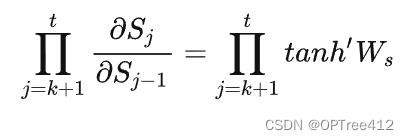
在这里插入图片描述

下图所示为tanh及其导数图像：
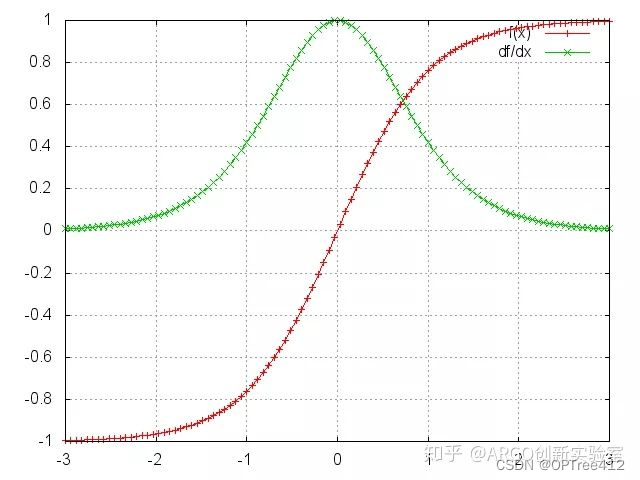
在这里插入图片描述
由上图可以看出tanh′≤1，在绝大部分训练过程中tanh的导数是小于1的，因为很少情况下会恰好出现WxXj+WsSj?1+b1=0。

如果Ws也是一个大于0小于1的值，则当t很大时，∏j=k+1 t tanh′Ws就会趋近于0。同理当Ws很大时∏j=k+1 t tanh′Ws就会趋近于无穷，这就是RNN中梯度消失原因。

举个例子：
小于1的数乘在一起，必然是越乘越小的。这才仅仅是3层，如果10层的话，根据0.25^10≈0.000000954 ，第10层的误差相对第一层卷积的参数 W1 的梯度将是一个非常小的值，这就是所谓的“梯度消失”.

2.3.2 梯度消失有啥问题呢？

简单说，当我们看到梯度趋近于0时，我们不能判断是时刻t和t+n之间没有依赖关系，还是参数的错误配置导致的。

2.3.3 换个激活函数会怎么样呢？（梯度爆炸）

sigmoid函数和tanh函数相比呢？
sigmoid函数的导数介于[0,0.25]之间，tanh函数的导入为[0,1]之间，虽然他们两者都存在梯度消失的问题，但tanh比sigmoid函数的表现要好，梯度消失得没有那么快。

为什么RNN中不选用ReLU激活函数来彻底解决梯度消失的问题呢？

其实在RNN中使用ReLU函数确实也是能解决梯度消失的问题地，但是又会引入一个新问题梯度爆炸，先看看ReLU函数和其导数图：
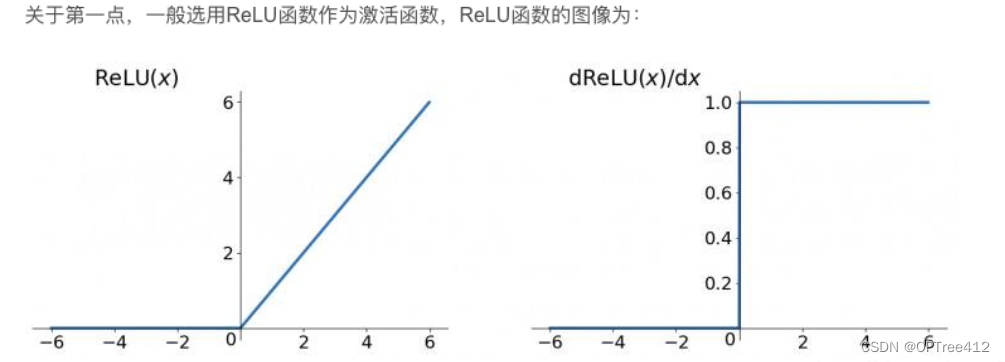
在这里插入图片描述
因为ReLu的导数恒为1，由上面推导的公式我们发现：激活函数的导数 x Ws（隐藏层权重）

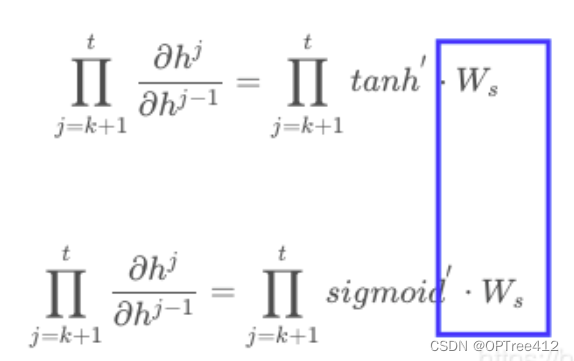
只要Ws的值大于1的话，经过多次连乘就会发生梯度爆炸的现象。但是这里的梯度爆炸问题也不是不能解决，可以通过设定合适的阈值解决梯度爆炸的问题。

对于梯度爆炸，Mikolov首先提出的解决方案是裁剪梯度，使它们的范数具有一定的最大值。
在这里插入图片描述

3. RNN的代码实战（基于pytorch）

3.1 nn.RNN()

在Pytorch中定义的RNN，其实是没有y这个输出层的。例如下图中，Pytorch版本的两个输出，output=[h1, h2, h3, h4], hn = h4。如果想要得到输出层y，可以自行加一个全连接层。
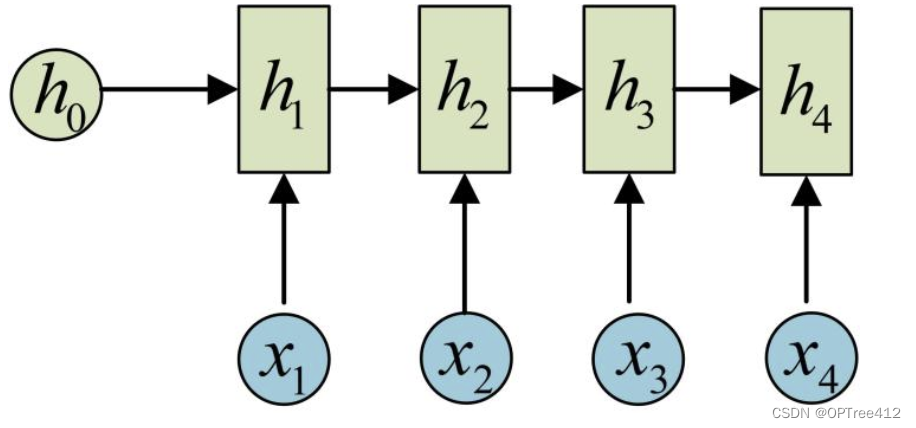
在这里插入图片描述

nn.RNN() 中最主要的参数是 input_size 和 hidden_size，这两个参数务必要搞清楚。其余的参数通常不用设置，采用默认值就可以了。

nn.RNN(input_size, hidden_size, num_layers=1, nonlinearity=tanh, bias=True, batch_first=False, dropout=0, bidirectional=False)

输入	样式	意义
input_size	`input_size=x`	`输入特征的维度`，一般rnn中输入的是词向量，那么 input_size 就等于一个词向量的维度
hidden_size	`hidden_size=h`	`隐藏层神经元个数，或者也叫输出的维度`（因为rnn输出为各个时间步上的隐藏状态）
num_layers	`num_layers=2`	网络的层数，`默认为1`
nonlinearity	`nonlinearity=‘'tanh'’`	激活函数，可以是tanh或relu，`默认为tanh`
bias	`bias=False`	是否使用偏置，`默认为True`
batch_first	`batch_first=True`	输入数据的形式，`默认是 False`，就是这样形式`(seq(num_step), batch, input_dim)`，也就是将序列长度放在第一位，batch 放在第二位；如果是True，形式为`(batch,seq(num_step), input_dim)`
dropout	`dropout=1`	是否应用dropout, `默认为0，不使用`，如若使用将其设置成1即可
birdirectional	`birdirectional=True`	是否使用双向的 rnn，`默认是 False`

3.2 nn.RNN()的输入输出

输入shape :
input_shape = [时间步数, 批量大小, 特征维度] =[num_steps(seq_length), batch_size, input_size]

输出 :
在前向计算后会分别返回输出output和隐藏状态hidden

输出output指的是隐藏层在各个时间步上计算并输出的隐藏状态，它们通常作为后续输出层的输?。需要强调的是，该“输出”本身并不涉及输出层计算，形状为output_shape = [时间步数, 批量大小, 隐藏单元个数]=[num_steps(seq_length), batch_size, num_directions*hidden_size]；
隐藏状态hidden指的是隐藏层在最后时间步的隐藏状态：当隐藏层有多层时，每?层的隐藏状态都会记录在该变量中；对于像?短期记忆（LSTM），隐藏状态是?个元组( h , c ) ，即hidden state和cell state(此处普通rnn只有一个值)，隐藏状态h的形状为hidden_shape = [层数, 批量大小,隐藏单元个数] = [num_layers* num_directions, batch_size, hidden_size]

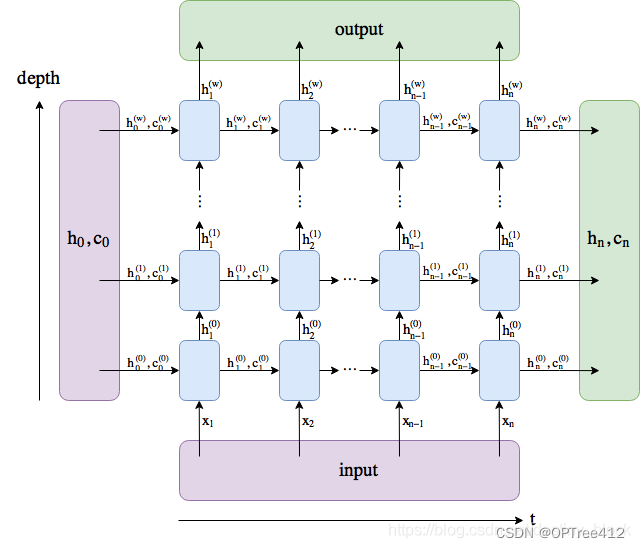
在这里插入图片描述
output 包括最后一层中的所有隐藏状态（“最后”深度方式，而不是时间方式，即所有时刻最后一层的隐层状态）。 (h_n, c_n) 包括最后一个时间步后的隐藏状态，所以你可以将它们送入另一个LSTM。