[人工智能][笔记]机器学习之机器学习模型及案例分析《一》

活动地址：CSDN21天学习挑战赛

前言

环境:
python3.7
IDEA

机器学习基本思路：

• 推导公式进行建模
• 优化模型
• 评估系数
• 根据模型进行预测

回归

1. 案例

一元线性回归的例子引出线性回归模型：
1920年汽车速度与刹车距的数据，现在，我们想研究速度与刹车距离之间到底有什么样的关系。

绘制散点图

# 1.收集数据
data_cars = pd.read_csv("../data/cars.csv",usecols = ["speed","dist"])
print(data_cars.head())

# 2.可视化
speed = data_cars["speed"]
dist = data_cars["dist"]
plt.scatter(speed,dist) # 散射
plt.title("Scatter plot of vehicle speed and braking distance")
plt.show()

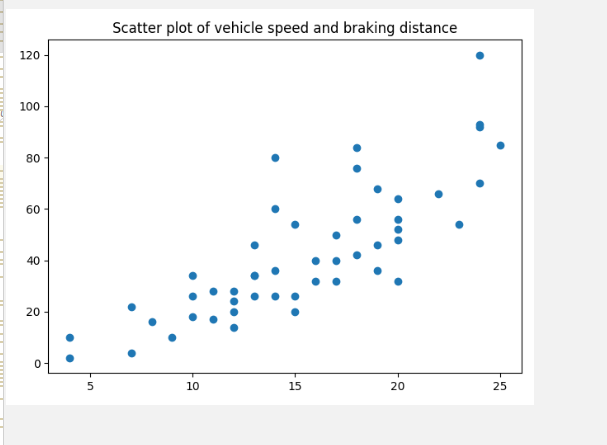
呈现线性关系：

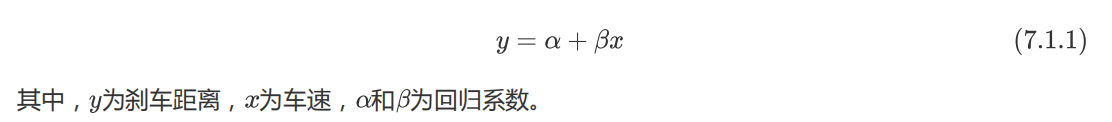
为了使预测更为精准

从图像直观描述，就是使寻找一条直线，使得所有样本点到直线的距离之和最短，如图7.1.2所示：

以下在机器学习中称为损失函数：

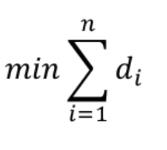
损失函数

我们可以通过直接法和迭代法两种方式对该损失函数进行优化，进而得到使损失函数最小的回归系数。下面，我们分别用这两种方法进行求解。

直接法

直接法，就是直接给出优化问题的最优解，并不是所有的优化问题都可以用直接法得到最优解，如果要
使用直接法，损失函数需要满足两个条件：
1. 损失函数为凸函数； （曲线是凹状或者凸状）
2. 损失函数为解析解，即通过严格的公式所求得的解。

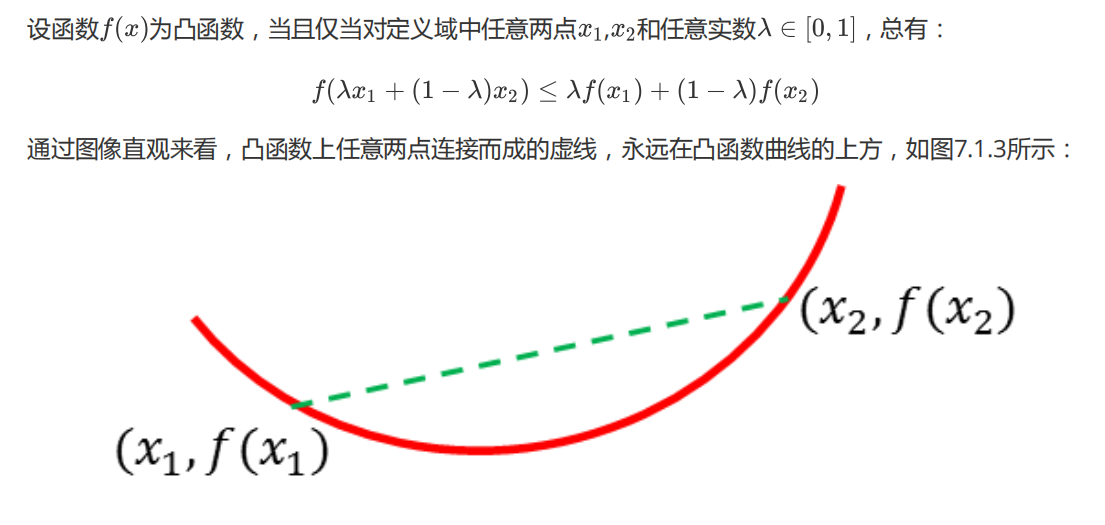
凸函数定义:

图7.1.3 凸函数曲线图

python代码：

## 2.2 损失函数
import sympy
#设定回归系数
alpha, beta = sympy.symbols("alpha beta")

#设定损失函数
L = 0.5* np.sum((dist - beta*speed - alpha)**2)

#求偏导
print(sympy.diff(L, alpha))
#50.0*alpha + 770.0*beta - 2149.0
print(sympy.diff(L, beta))
#770.0*alpha + 13228.0*beta - 38482.0
f1 = sympy.diff(L, alpha)
f2 = sympy.diff(L, beta)

### 求解线性方程组
outcome = sympy.solve([f1, f2], [alpha, beta])
print(outcome)
#{alpha: -17.5790948905109, beta: 3.93240875912409} 最优解

{alpha: -17.5790948905109, beta: 3.93240875912409} 最优解

我们将直线 y = 3.932x+ -17.570 绘制在车速与刹车距离散点图中，如图7.1.5所示。

### 绘图
alpha_num = outcome[alpha]
beta_num = outcome[beta]

dist_pre = beta_num*speed + alpha_num
plt.scatter(speed, dist)
plt.plot(speed, dist_pre, c = "r")
plt.title("Fitting results")
plt.show()

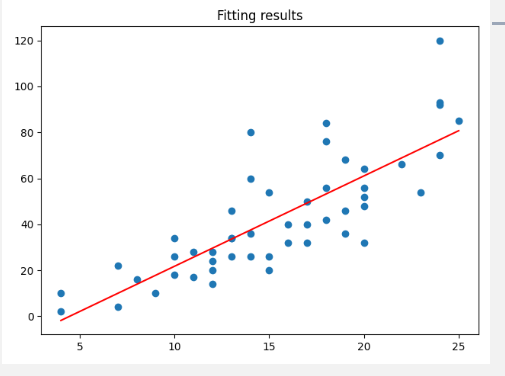
迭代法

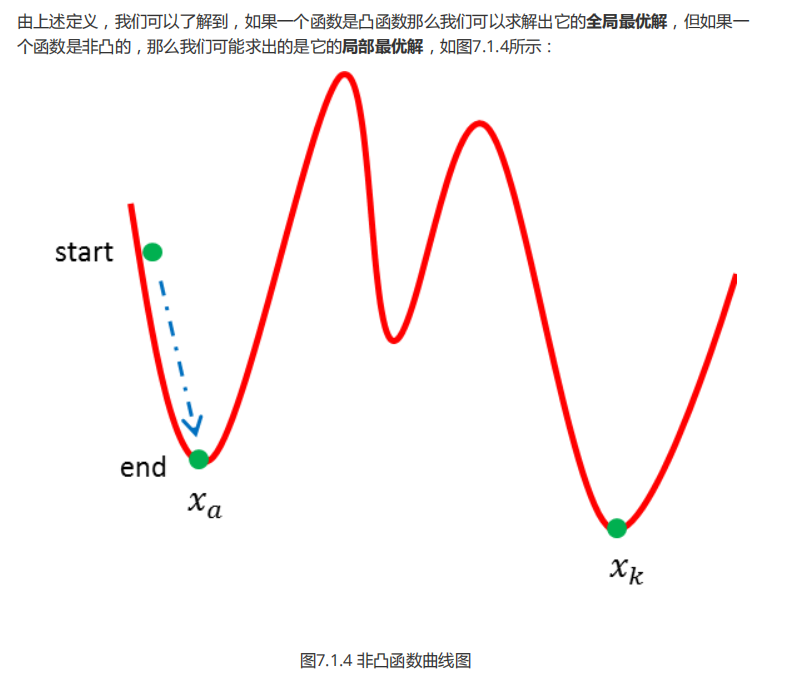
很多情况都是非凸形的 没法使用直接法进行优化 所以我们可以使用迭代法求解。迭代法是一种不断用变量的旧值递推新值的过程，即迭代的用旧值修正对最优解的估计。

这里，我们使用迭代法中的小批量梯度下降法解决问题：

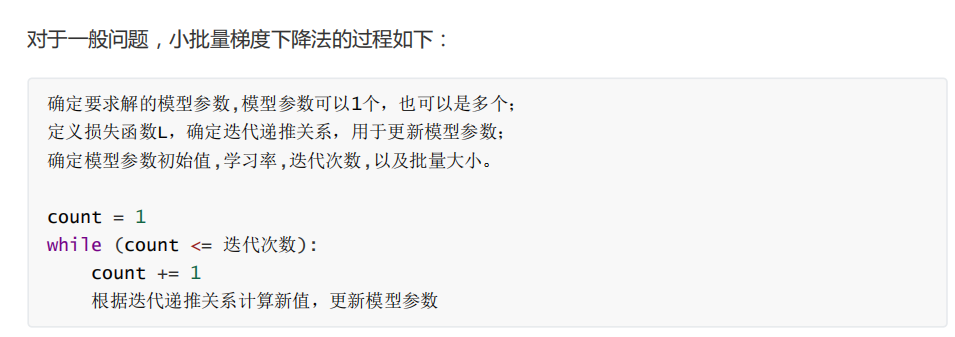
对于我们的问题，小批量梯度下降法的过程如下：

1. 确定要求解的模型参数为 α,β ；

2. 定义小批量梯度下降法的损失函数：
   

3. 求解梯度，并定义递推关系：
   
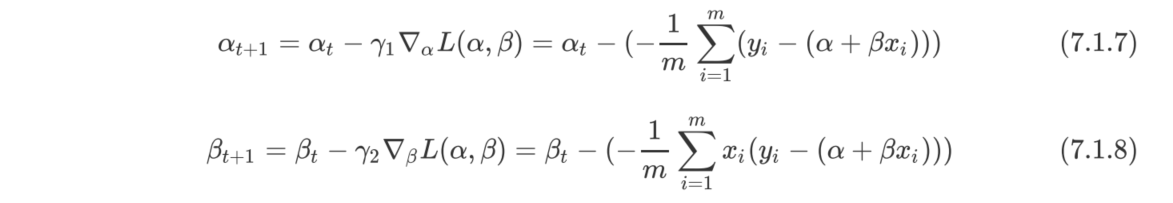
   在[0, 10)中按照均匀分布随机产生alpha和beta的初始值，定义学习率 和 均为0.02，定义迭代次数
   为20000次；

4. 迭代，迭代完成输出最后的模型参数。

#迭代法
import random

#定义递推关系,更新迭代变量
def update_var(old_alpha, old_beta, y, x, learning_rate):
    len_x = len(x)
    alpha_delta = np.sum(-(y - old_beta*x - old_alpha))/len_x
    beta_delta = np.sum(-x*(y - old_beta*x - old_alpha))/len_x
    new_alpha = old_alpha - learning_rate*alpha_delta
    new_beta = old_beta - learning_rate*beta_delta
  
    return (new_alpha, new_beta)

#迭代
def iterative_func(y, x, start_alpha, start_beta,
                   learning_rate, iterative_num, 
                   sample_num):
    alpha_list = []
    beta_list = []
    alpha = start_alpha
    beta = start_beta
    num_list = list(range(1, len(y)+1))
    for i in range(iterative_num):
        alpha_list.append(alpha)
        beta_list.append(beta)
        random.shuffle(num_list)
        
        index = num_list[:sample_num]
        alpha, beta = update_var(alpha, beta, 
                                 y[index], x[index], learning_rate)
#        print("alpha: {}, beta:{}".format(alpha, beta))
    return (alpha_list, beta_list)

#在[0, 10)之间按照均匀分布随机产生alpha和beta的初始值
start_alpha = np.random.random()*10
start_beta = np.random.random()*10

#设置学习率为0.01,迭代次数为500次,每次计算8个数据
learning_rate = 0.002
iterative_num = 20000
sample_num = 16

alpha_list, beta_list = iterative_func(dist, speed, start_alpha, start_beta,
                                     learning_rate, iterative_num,
                                     sample_num)

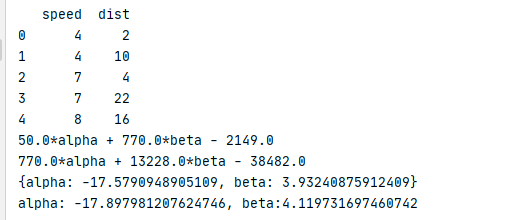
最后会发现直接法和迭代法 答案相近

最后绘制α和β变化：

...代码接上...
#写出
import csv
parameter_data = zip(alpha_list, beta_list)
with open("./outcome/gradient_descent_parameter.csv", 'w', newline = '') as f:
    csv_writer = csv.writer(f)
    csv_writer.writerow(["alpha","beta"])
    csv_writer.writerows(parameter_data)
#绘图
plt.subplot(121)
plt.plot(alpha_list)
plt.title("alpha change process")
plt.subplot(122)
plt.plot(beta_list)
plt.title("beta change process")
plt.show()

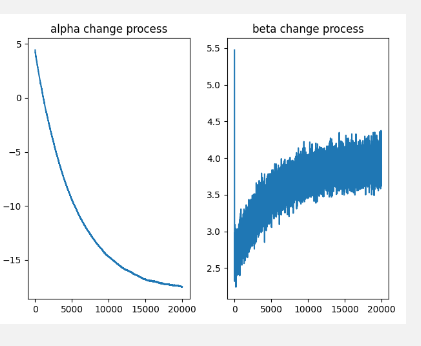
学习率：影响变化稳定的因素，我们可以设置其学习率随着迭代次数增加逐渐递减，来缓解这种现象
样本数：
迭代次数：

评估数据好坏

直接法求得的回归系数估计值进行评价，即计算其 R^2:

#判定系数R2
dist_pre = beta_num*speed + alpha_num
dist_mean = np.mean(dist)
R_2 = np.sum((dist_pre - dist_mean)**2)/np.sum((dist - dist_mean)**2)
print(R_2)
#0.651079380758251

#预测
new_speed = pd.Series([10, 20, 30])
new_dist_pre = beta_num*new_speed + alpha_num
print(new_dist_pre)

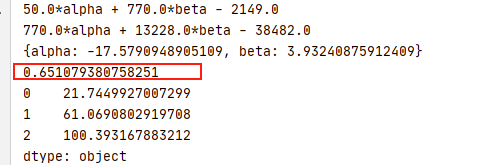
结果R^2得到0.65107938

预测

利用我们的模型对结果进行预测。
我们依然采用直接法求得的回归系数估计值，对新的样本进行预测。

假设新记录的一批车辆的车速分别为10, 20, 30，利用python，我们可以得到刹车距离的预测值为21.745，61.069，100.393。

2. 回归的基本思想

多元线性回归

在上面的例子中，我们仅有一个自变量，但是在现实生活中，我们要分析的不只是一个，而是多个自变
量与因变量之间的关系，对于这种预测任务，我们可以采用多元线性回归.

我们的目的是让机器从数据中学习出一个最优模型，从而进行预测，但是机器不会自动的学习，它需要
被注入灵魂，需要在人的指导下去工作。

所以，我们需要告诉机器如何学习，即定义一系列"策略"让机器围绕着这种"策略"不断地学习，更新自己。比如，在多元线性回归的问题中，我们的"策略"如下：

• 定义损失函数，描述模型好坏
• 利用算法最小化损失函数

损失函数

定义：

最小二乘法

梯度下降法

梯度下降法就是利用一阶泰勒展开，使 一步步逼近最优，从而最小化损失函数的方法。

在梯度下降法中，由于每次迭代带入损失函数中样品个数的不同，我们又可将其分为:

• 批量梯度下降法(BGD)，
• 小批量梯度下降法(MBGD)
• 随机梯度下降法(SGD)。

1.3 辛烷值预测案例

某石化企业的催化裂化汽油精制脱硫装置运行4年，积累了大量历史数据。从催化裂化汽油精制装置
中，我们得到了325个数据样本，因变量为产品中的辛烷值(RON)(y)，自变量有310个（x1,x2,x3…x310），它们分别为生产前
的原材料含量和各种操作变量。

# -*- coding: utf-8 -*-

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn import metrics
from mlxtend.evaluate import bias_variance_decomp

#读取原始数据
data_ron = pd.read_csv("../data/data_ron.csv")
print(data_ron.shape)
#(325, 311)
y = data_ron["RON"]
X = data_ron.iloc[:, 1: (len(data_ron) + 1)]

X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    test_size = 0.2, random_state = 10)


#构建模型
model = LinearRegression()
model.fit(X_train, y_train)
print(round(model.score(X_train, y_train), 4))
print(round(model.score(X_test, y_test), 4))


#标准化(随机梯度下降法之前需要标准化)
#stand_train = StandardScaler()
#stand_train.fit(X_train)
#X_train_standard = stand_train.transform(X_train)
#X_test_standard = stand_train.transform(X_test)
#model = SGDRegressor()
#model.fit(X_train_standard, y_train)
#print(round(model.score(X_train_standard, y_train), 4))
#print(round(model.score(X_test_standard, y_test), 4))


def mape(y_true, y_pre):
    n = len(y_true)
    mape = (sum(np.abs((y_true - y_pre)/y_true))/n)*100
    return mape

y_hat = model.predict(X_test)
MSE = metrics.mean_squared_error(y_test, y_hat)
RMSE = metrics.mean_squared_error(y_test, y_hat)**0.5
MAE = metrics.mean_absolute_error(y_test, y_hat)
MAPE = mape(y_test, y_hat)


print("MSE:{:.4f}, RMSE:{:.4f}, MAE:{:.4f}, MAPE:{:.4f}".format(MSE, RMSE, MAE, MAPE))
#MSE:0.0370, RMSE:0.1924, MAE:0.1511, MAPE:0.1710

#不进行转换会报错
X_train = np.array(X_train)
y_train = np.array(y_train)
X_test = np.array(X_test)
y_test = np.array(y_test)

mse, bias, var = bias_variance_decomp(model, X_train, y_train, X_test, y_test,loss='mse',
                                      num_rounds=30, random_seed=1)

print("mse:{:.4f}, bias:{:.4f}, var:{:.4f}".format(mse, bias, var))
#mse:0.3947, bias:0.3443, var:0.0504

主要使用sklearn的模型

可以看到，我们在训练集上的模型得分居然是1.0，这是不是说明我们的模型构建的足够好呢？不急，
我们再看看模型在测试集上的得分。

由结果可知，模型在测试集上的得分为负数，已经足够差了。这种在训练集上表现好，但在测试集上表现差的现象，我们称为过拟合，与其相对的就是在训练集上表现差，但在测试集上表现好，这种我们称之为欠拟合，

1.4 过拟合与欠拟合

泛化

定义：得出的模型能够对测试集进行准确预测，那么我们就说它具有较好的泛化能力。

就是模型的通用性很强，在测试集里面预测准确。

过拟合与欠拟合

过拟合

定义：由于我们使用过多的因变量，而导致训练集得分很高，测试集得分很低，这就是出现了过拟合的情况。

欠拟合

定义：
当我们的模型过于简单时，可能会出现欠拟合的情况，这说明了我们的训练不够充分，模型没有抓住训
练集中数据的信息。如果在上面的案例中，我们的模型出现了欠拟合，那么在训练集上，迫性的得分应
该较低，而测试集上的模型得分应该较高。

规避的方法：
遇到欠拟合时，我们应该适量增加模型的复杂度，来避免欠拟合的状况。

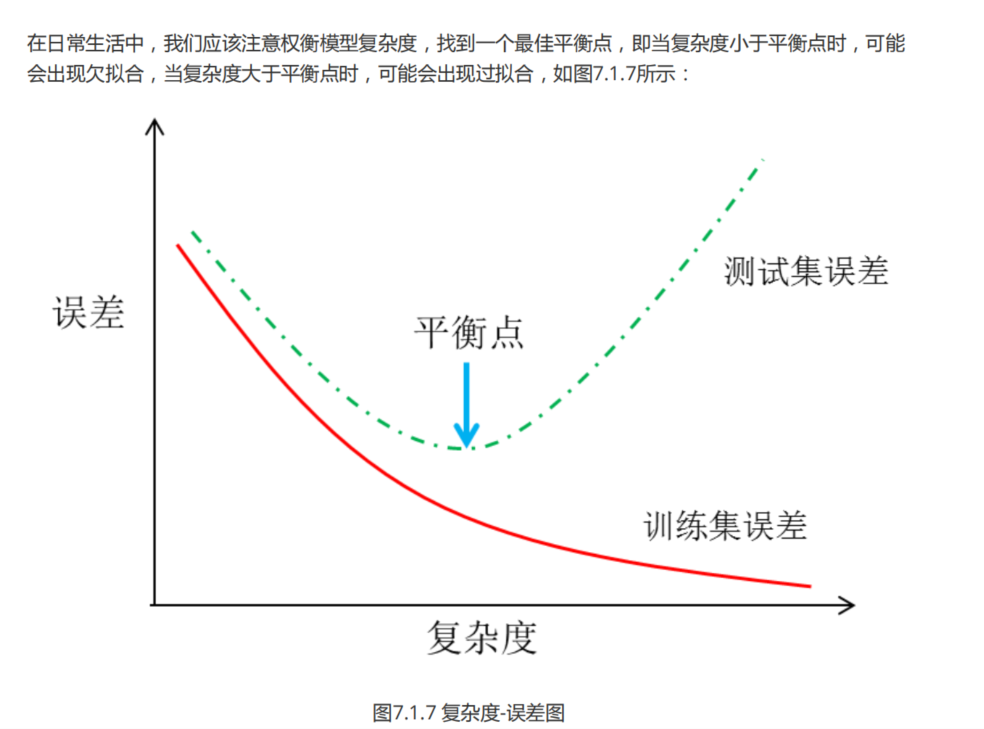
复杂度小于平衡点，欠拟合；
复杂度大于平衡点，过拟合；

简化回归模型

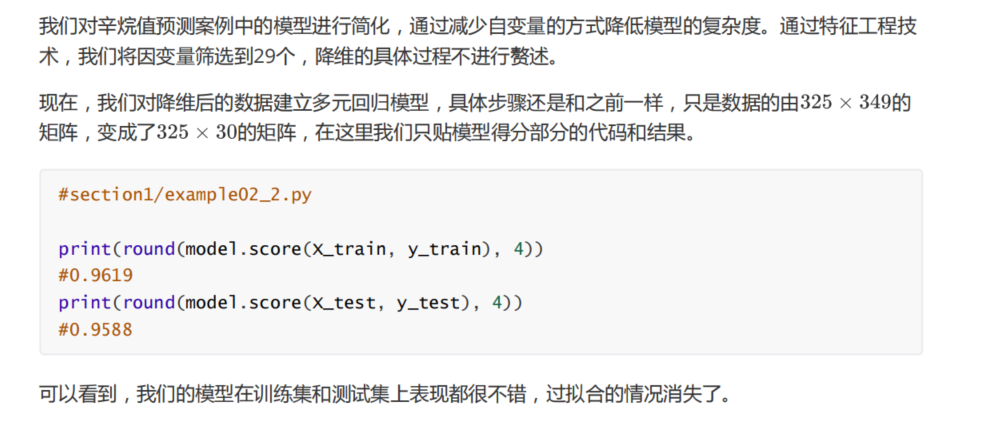
1.5 模型的评价

R^2

MSE和RMSE

MAE和MAPE

偏差-方差权衡(仔细研究一下)

评价回归模型

1.6 正则项

在建模时，我们总是希望自己的模型能够尽量在训练集上取得较高的精度，又希望模型有好的泛化能
力，这时，我们可以通过给损失函数添加正则项实现这一目标。正则项的使用可以减缓过拟合的状况，
也可以帮助我们选择模型的特征。

岭回归

Lasso回归

ElasticNet回归

python实现

总结

工具：

• 基于网页的用于交互计算的应用程序 Jupyter Notebook ___ 还可以写C++

文献管理工具：

• Mendeley Desktop
• Zotero

模型管理工具：

• DVC

?常用网站：

• 免费软件机器学习库 scikit-learn.org

参考：
机器学习理论及案例分析(part2)–回归