1 神经元模型

在生物神经网络中，一个神经元A与其他神经元相连。当它兴奋时，会向相连的神经元B发送化学物质改变相连神经元B的电位。相连神经元B的电位超过阈值则会被激活开始兴奋，然后向相连的神经元C发送化学物质。
MP神经元模型
$\sum\limits_{i = 1}^{n} w_ix_i$ 表示相连神经元对当前神经元电位的影响， $f(\sum\limits_{i = 1}^{n} w_ix_i - \theta)$ 表示当前神经元电位超过或没超过阈值时的输出。这里的函数f称为激活函数。理想激活函数应该是阶跃函数，即电位超过阈值时输出为1，没超过阈值时输出为0。但是阶跃函数不连续不光滑，不利于后期参数学习，因此使用sigmoid函数以及其他函数作为激活函数。

2 感知机和多层网络

学习了神经元模型之后，开始学习如何利用神经元模型构建神经网络模型。先从最简单的感知机模型和逻辑回归模型开始学习。在李航《统计学习方法》中，感知机模型的数学表达式为： $\sum \limits_{i = 1}^{n}w_ix_i + b$ ，逻辑回归模型数学表达式为： $\frac{1}{1 + e^{-\sum w_ix_i + b}}$ 。

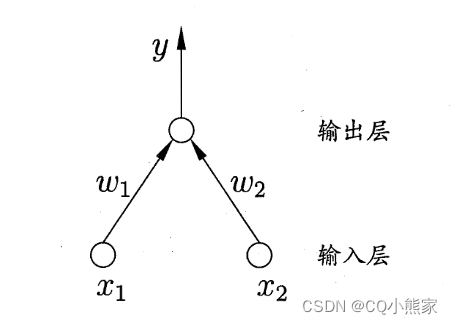
如果上图所示神经网络模型使用的激活函数是恒等函数，那么该神经网络模型等价于感知机模型；如果使用的激活函数是sigmoid函数，那么该神经网络模型等价于逻辑回归模型。数学证明，对于线性可分问题，两层的感知机模型一定可以求解。对非线性可分问题，可以通过增加网络层数、使用非线性激活函数等方法进行求解。非线性问题求解的本质是对特征空间进行变换，将非线性问题转为线性问题。

3 误差反向传播算法

多层网络的学习使用误差反向传播算法。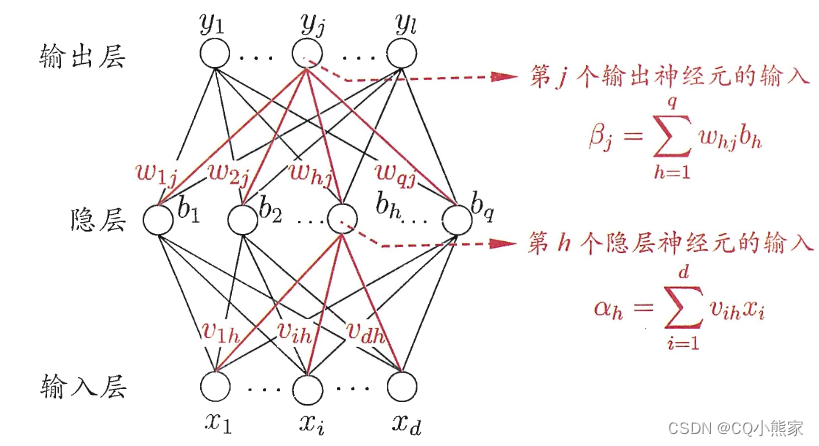 BP网络
BP推导
BP伪代码
这里的伪代码是根据每个样本的误差更新一次参数，这是标准BP算法；还有一种算法是根据所有样本的累计误差更新一次参数，称为累计误差BP算法。累计误差BP算法更新次数少，但是当累计误差下降到一定程度时，后续下降会非常缓慢，此时标准BP表现较好，下降速度较快。
BP神经网络学习能力强大，理论上只要隐藏层神经元个数做够多，就可以学得任意复杂度的连续函数。但是学习能力太强容易过拟合，有两种方法可以避免过拟合。一种是早停，使用训练集训练，使用验证集判断是否过拟合。当训练误差减小，但是验证误差增大时，认为网络模型开始过拟合，停止训练。一种是正则化，在目标函数中加入模型复杂度的惩罚项以均衡模型复杂度和误差。

4 局部极值点和鞍点

BP算法使用梯度下降法更新参数，当参数更新到局部极小值点或者鞍点处，梯度为零，没法继续更新参数。可以通过随机初始化点、随机梯度下降法（给梯度附加一个随机值）来避免进入局部极值点和鞍点。

5 其他神经网络

其他与标准神经网络不同，不同的地方包括激活函数不同，如RBF网络；网络结构不同，如Elman网络；目标函数不同，如玻尔兹曼机；
深度学习中的神经网络隐藏层层数较多而非隐藏层神经元数目较多。这样的好处是不仅有更多的神经元，而且激活函数之间还有嵌套，更有利于学习非线性函数。但是网络层数较多时，反向传播不容易收敛，可以通过无监督逐层训练（DBN）或者权值共享（CNN）来解决。