[人工智能]Pytorch深度学习（一）：前馈神经网络（FNN）

Pytorch深度学习（一）：前馈神经网络（FNN）

参考B站课程：《PyTorch深度学习实践》完结合集
传送门：《PyTorch深度学习实践》完结合集

一、线性模型：

已知数据：
$$x=[1,2,3],y=[2,4,6]$$
预测$x=4$时，$y$等于多少
建立线性模型
$$\hat{y}=w?x,x,\hat{y}\in \mathbb{R}$$
估计权重$w$（weight），再来预测$x=4$时$y$的值。
定义MSE（Mean Square Error）：
$$cost=\frac{1}{N}\sum _{n=1}^N({\hat{y}}_n?y_n{)}^2$$

二、普通方法

在可能的区间内$(0,4.1)$内遍历来试探最优的权重$w$使得误差MSE最小

import numpy as np
from matplotlib import pyplot as plt

xdata = [1, 2, 3]
ydata = [2, 4, 6]

def forward(x):
    return x * w

def loss(x, y):
    ypred = forward(x)
    return (ypred-y)**2

wlist = []      # weight
mse = []    # mean squre error
for w in np.arange(0, 4.1, 0.1):
    print('w=', w)
    lsum = 0
    for x_val, y_val in zip(xdata, ydata):
        ypred_val = forward(x_val)
        lossval = loss(x_val, y_val)
        lsum += lossval
        print('\t', x_val, y_val, ypred_val, lossval)
    print('MSE=', lsum/3)
    wlist.append(w)
    mse.append(lsum/3)

plt.plot(wlist, mse)
plt.ylabel('Mean squre error')
plt.xlabel('weight')
plt.show()

可见最佳的权重在2.0附近，但这种算法是不够好的，首先区间不好找，其次遍历的步长会影响精度，并且遍历会耗费了大量的计算力。

三、梯度下降法(Gradient Descent)

这是经典的优化算法，在局部确定MSE下降速度最快的方向（梯度的反方向）来求得局部解.
$$cost=\frac{1}{N}\sum _{n=1}^N({\hat{y}}_n?y_n{)}^2=\frac{1}{N}\sum _{n=1}^N(x_n?w?y_n{)}^2$$
则梯度方向
$$\frac{?cost}{?w}=\frac{2}{N}\sum _{n=1}^N{x}_n(x_n?w?y_n)$$
更新权重$w$
$$w=w?0.01?\frac{?cost}{?w}$$
其中，0.01是学习率，其不宜取得过大

import numpy as np
from matplotlib import pyplot as plt

xdata = [1, 2, 3]
ydata = [2, 4, 6]

w = 1.0     # stating weight
costlist = []

def forward(x):
    return x * w

def cost(xs, ys):
    cost = 0
    for x, y in zip(xs, ys):
        ypred = forward(x)
        cost += (ypred - y) **2
    return cost / len(xs)

def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w -y)
    return grad / len(xs)

print('Predict(before training', 4, forward(4))     # starting value

for epoch in range(100):
    cost_val = cost(xdata, ydata)
    costlist.append(cost_val)
    grad_val = gradient(xdata, ydata)
    w -= 0.01 * grad_val    # study rate = 0.01
    print('Epoch:', epoch, 'w=', w, 'loss=', cost_val)

print('Predict(after training)', 4, forward(4))

plt.plot(range(100), costlist)
plt.xlabel('epoch')
plt.ylabel('cost')
plt.title('Gradient Descent')
plt.show()

可见收敛效果较好。最后一步输出的权重以及，预测值如下

Epoch: 99 w= 1.9999444396553017 loss= 1.752432687141379e-08
Predict(after training) 4 7.999777758621207

四、随机梯度下降法（Stochastic Gradient Descent）

正如前所言，DG算法可能陷入局部，一旦碰到拐点等情况就没有办法求到全局最优，于是引入随机梯度下降法
优点：有可能避免陷入局部最优
缺点：计算量比DG更大

import numpy as np
from matplotlib import pyplot as plt

xdata = [1, 2, 3]
ydata = [2, 4, 6]

w = 1.0     # stating weight
costlist = []

def forward(x):
    return x * w

def loss(x,y):
    ypred = forward(x)
    return (ypred - y) ** 2

def gradient(xs, ys):
    return 2 * x *(x*w -y)

print('Predict(before training', 4, forward(4))     # starting value

for epoch in range(100):
    for x,y in zip(xdata, ydata):
        grad = gradient(x,y)
        w = w - 0.01*grad
        print('\t grad :', x, y, grad)
        l = loss(x,y)
    print('progress:', epoch, 'w=', w, 'loss=', l)
    costlist.append(l)


print('Predict(after training)', 4, forward(4))

plt.plot(range(100), costlist)
plt.xlabel('epoch')
plt.ylabel('cost')
plt.title('Stochastic Gradient Descent') 
plt.show()

progress: 99 w= 1.9999999999999236 loss= 5.250973729513143e-26
Predict(after training) 4 7.9999999999996945

可以看到同样的迭代步数，SDG算法最后产生的误差的数量级比DG算法更小

我们比较两种算法的误差图像：

但SDG算法存在计算量相对大的缺点，所以在实际应用当中可以部分数据用DG，部分数据用SDG。

五、前馈神经网络（FNN）

以上就是一个简单的前馈神经网络的例子，它的第一次“学习”过程如下：

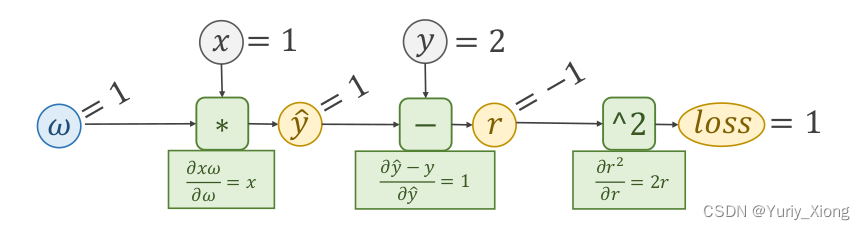
这里由于我们推导出了误差（MSE）关于权重$w$的解析式 $$\frac{?cost}{?w}=\frac{2}{N}\sum _{n=1}^N{x}_n(x_n?w?y_n)$$所以带入相关数据和即可得到梯度值，从而更新$w$。然而实际情况可能更为复杂，不一定能直接求出解析式，仔细观察我们知道：

• 我们不一定非得得到解析式，只需要得到每一次误差 $loss$ “反馈” 给权重$w$的值，用于更新$w$

这就是反馈神经网络（BPNN）的基本思想，具体见下一篇文章。