
近年来,关于AI for Science的主题被广泛讨论,重点领域包含使用AI方法加速设计并发现新材料,助力高能物理及天文领域的新问题探索,以及加速智慧工业实时设备数据与模型的“数字孪生”等等[1]。
面向上述科学计算的技术趋势和新兴场景的发展,百度飞桨致力于帮助科研人员在科学领域完成新的探索,并助力企业完成工业落地。由此,飞桨于春季5月20日WAVE SUMMIT峰会上正式发布了科学计算工具组件赛桨PaddleScience v1.0 Beta,针对传统数值计算方法面临的维数高、时间长、跨尺度的挑战,基于飞桨核心框架自动微分机制,综合数学计算与物理数据相结合的处理方法,赛桨提供物理机理约束的PINNs(物理信息神经网络)方法求解模型,可在计算流体力学(CFD)领域中完成经典流场仿真分析,并加速求解偏微分方程,最终提升智能制造系统设计、建模仿真、分析优化等技术的产业化落地能力。
赛桨 PaddleScience v1.0 Beta 包含了如下三方面的重要发布:
-
**丰富的场景案例:**提供圆柱绕流、涡激振动及方程反演等多个经典流体力学案例,支持直接复用及二次开发。
-
**API****升级更新:**提供用户自定义偏微分方程接口及边界条件定义功能,支持基础2D&3D几何定义,并支持自动并行及动静态图的运行模式等。
-
**框架技术创新:**在自动微分、分布式、编译器、执行器等方面进行技术创新,有力支撑科学计算任务高效训练和推理。
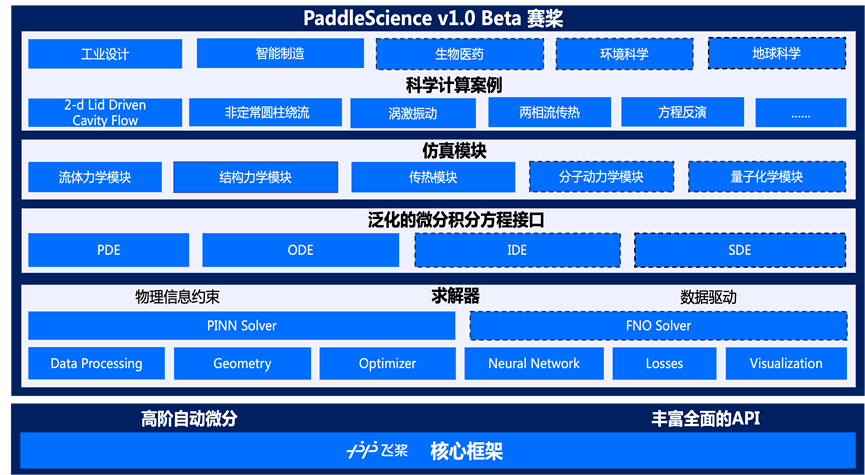
PaddleScience v1.0 Beta产品全景
丰富的案例场景
PaddleScience使用物理信息神经网络(PINNs)的方法,基于飞桨深度学习框架,将物理信息融入神经网络。重点深耕计算流体力学(CFD)的学科场景,为科研提供新的解决思路。PaddleScience当前提供的多个经典计算案例,包括2D顶盖驱动方腔流(Lid-Driven Cavity Flow)、非定常圆柱绕流、涡激震动、方程反演等经典流体问题。
2D&3D 非定常圆柱绕流
该算例提供了使用飞桨进行流体力学中经典的圆柱绕流2D&3D模型完整示例代码,基于物理信息神经网络PINNs的方法构建CFD求解器,并利用开源CFD工具OpenFoam产生的少量流场监督数据。2D圆柱绕流算例中,在NV-V100(32G)单卡训练近8h后,完成Re100工况下多个卡门涡脱落周期内的流场结构复现,同时相同精度下,对比OpenFoam(CPU-i5单线程下)执行下一30个时间步的计算速度,神经网络模型(NV-V100(32G))推理速度提升近12000倍,体现了基于PINNs方法在该问题上的快速推理能力。该项目可表明基于深度学习的方法可以应用于流体领域中飞行器、结构等气动外形的设计及优化等问题。
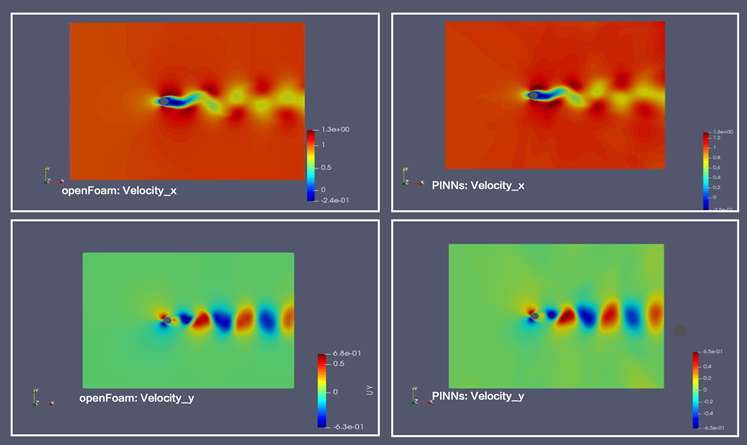
2D 非定常圆柱绕流案例:图 Re=100的2D圆柱绕流结果
(左:OpenFoam结果,右:PINNs方法结果)
涡激振动
该算例提供了使用飞桨进行涡激振动中结构特征反演模型的完整示例代码,基于涡激振动试验装备中采集的结构振动与受力信息,利用PINNs方法,构建结构刚度、阻尼的反演网络。一方面实现了结构特征的高精度预测(与真实值相对误差均小于2%),另一方面可真实复现下一时刻的流场信息。该项目可进一步应用于如流固耦合问题中气动弹性、流致振动等结构负载分析及设计优化等问题。
方程反演
该算例提供了使用飞桨进行等离子体弗拉索夫方程反演的完整示例代码,实现思路为利用物理信息神经网络PINNs解决反问题的优势,将神经网络融合物理信息,配合少量监督数据,快速完成等离子体相空间方程反演,并体现反演实际物理量如电场强度等优势。该项目可进一步用于支持模拟卫星电推力器产生的等离子体,分析等离子体对航天器敏感元件的影响。
科学计算工具组件API升级更新
赛桨 (PaddleScience) v1.0 Beta在功能及API层面做了如下大幅更新,从而支撑更多场景下的应用。
完善的方程求解功能及接口
- 支持使用连续时间方法及离散时间方法求解非稳态方程:
对于非稳态方程,连续时间方法将时间和空间均视为网络的输入。离散时间方法首先使用数值(隐式)方法对时间离散,得到仅包含空间变量的稳态方程,进而使用PINNs方法求解稳态方程,基于n时刻的已知状态(3个方向的速度)已知,求解n+1时刻的状态(3个方向的速度)。
- 新增符号化方程输入接口:
赛桨预定义了一些常用的方程,如N-S方程,Laplace方程等,同时也提供了自定义输入方程的接口,如下例子展示了如何使用该接口定义一个2D的Laplace方程。可在实例化PDE模块后分别定义自变量和因变量;使用python sympy模块定义方程,其中u.diff(x)表示因变量u关于自变量x的一阶导数,u.diff(x).diff(x)表示因变量u关于自变量x的二阶导数。
- 新增边值条件及初值条件接口:
赛桨新增了边值条件模块,并预置了Dirichlet/Neumann/Robin边值条件,仅需定义边值条件,并通过"set_bc" 接口将其指定到对应边界即可。对于非稳态方程,以类似方式增加了初值条件模块。
丰富的3D空间几何形状及可视化功能
赛桨新增了三维常用的几何形状,如立方体、立方体除去圆柱等。同时扩展了VTK可视化支持及支持空间随机离散。
一键切换的运行模式
- 支持使用分布式自动并行:
使用自动并行技术实现分布式计算内嵌在赛桨中,无需特别设置,即可实现并行化。
- 支持动态图、静态图:
赛桨后端同时支持动态图和静态图模式,可以通过简单的接口进行切换,在静态图模式可以获得更好的性能表现。
灵活的配置接口
- 新增网络初始化接口:
赛桨新增了初始化网络权重的接口 initialize(),支持从文件读取权重进行初始化,以及使用飞桨预制初始化函数(paddle.nn.initializer)进行初始化。
- 更加灵活的Loss配置接口:
赛桨提供了更加灵活的Loss设置方式,允许灵活直观的配置总体Loss。
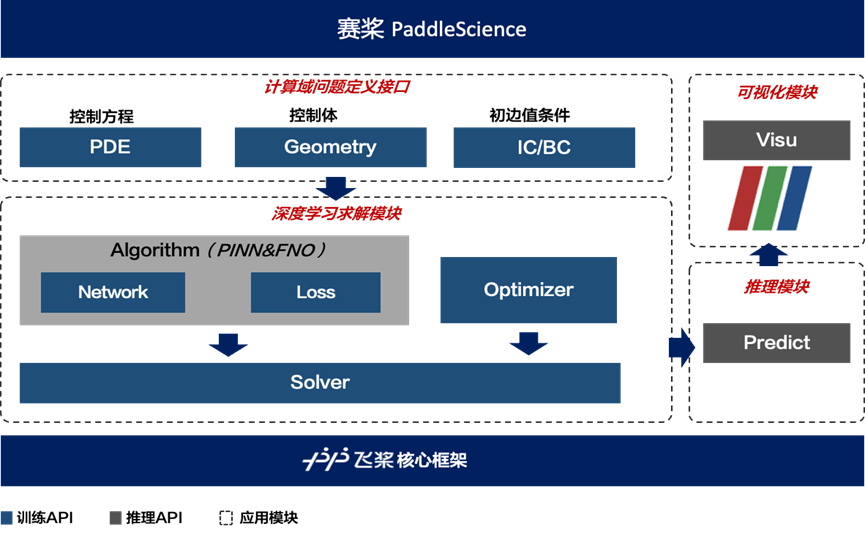
PaddleScience科学计算工具组件设计架构
框架技术创新
赛桨PaddleScience底层基于端到端的飞桨深度学习核心框架。为了有力支撑科学计算任务高效训练和推理,飞桨框架在自动微分、分布式、编译器、执行器等方面分别进行了技术创新。值得一提的是,自动微分功能升级带来了框架计算量方面的优化,结合自研编译器CINN,大幅提升性能。
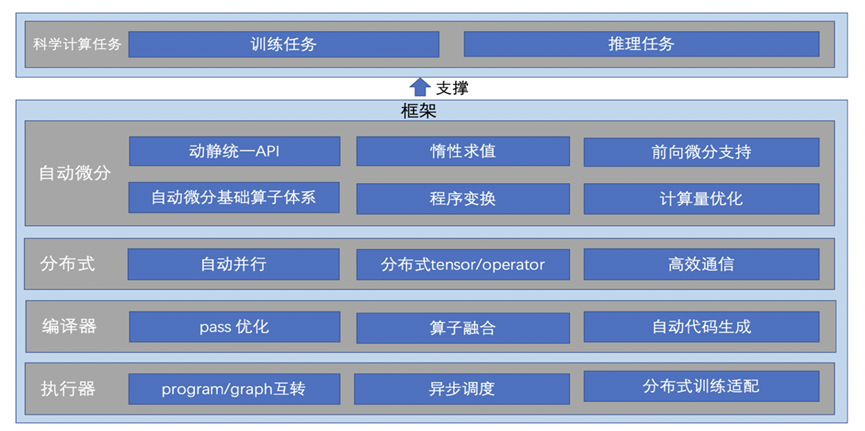
框架技术创新
- 自动微分功能:
新增对前向微分的支持,实现前反向不限阶的自动微分。用户完成前向组网后,会首先将前向过程对应的网络转化到自动微分基础算子体系上,然后多次调用linearize和transpose两种程序变换实现高阶前向/反向微分,最后将网络整体转化到飞桨原有phi算子体系上完成组网或者对接编译器进行更多优化。
- 自动微分API:
提供forward_grad和grad两个API分别支持前向微分和反向微分。提供Jacobian、Hessian两个API完成完整的一阶和二阶微分求解,支持按行延迟计算,在复杂偏微分方程组中显著提升计算性能。
- 分布式自动并行:
采用了高可扩展的飞桨自动并行技术,根据用户输入的串行网络模型和所提供集群资源信息自动进行分布式训练,在3D非定常圆柱绕流任务上32卡扩展效率可达到93%。
- 编译器:
使用通用Pass优化、算子融合以及代码生成技术,开启飞桨神经网络编译器CINN在2D定常laplace模型上实测有最大3.72倍性能提升。
- 执行器:
对典型的科学计算模型实现了Program和Graph两种表示结构的无损互转,打通了编译器优化和分布式训练结合的技术路径。
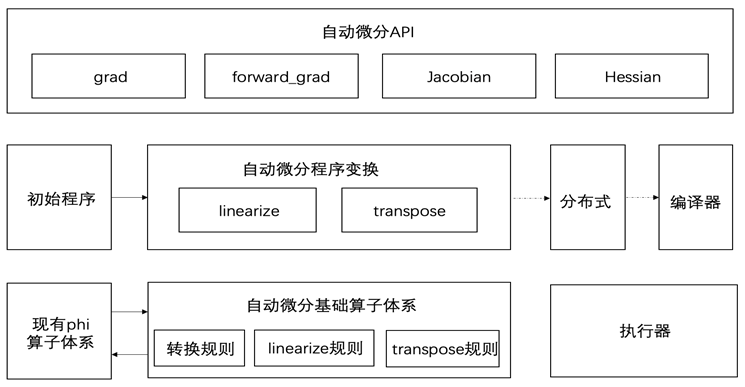
飞桨自动微分核心技术 基础算子体系与程序变换
性能分析
我们以2D定常laplace模型作为统一测试模型,设定采样点数100*100,选取多组网络层数和隐藏层节点数的全连接网络训练2000 epoch分别测试JAX和飞桨框架的性能,以JAX性能作为baseline计算飞桨框架相对于JAX的加速比。
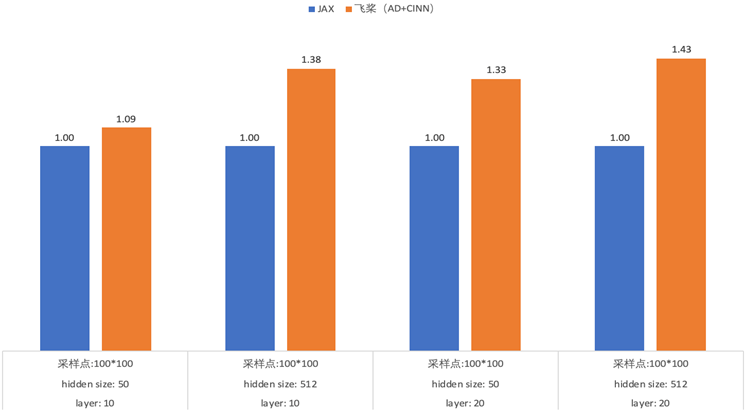
2D 定常laplace模型性能benchmark
(性能测试硬件平台:V100 16GB单卡;Intel? Xeon? Gold 6148 CPU@2.40GHz 40-core)
从实验结果可以看出, 受益于自动微分和编译器相关技术创新,飞桨框架在2D定常laplace模型上取得了优于JAX的性能。
加入飞桨PPSIG-Science小组
只要你对AI+科学计算有热爱,欢迎加入PPSIG-Science小组。这里汇聚了志同道合的朋友,协作完成项目,共同探索前沿。
- 飞桨科学计算PPSIG-Science小组:
https://www.paddlepaddle.org.cn/specialgroupdetail?id=9
- 更多关于PPSIG-Science请参考:
“先导杯”计算应用大奖赛
年度比赛盛事——第三届“先导杯”计算应用大奖赛正在如火如荼地进行中,百度飞桨发布AI for Science开放应用赛题,设置36万现金奖池,提供赛桨PaddleScience和螺旋桨PaddleHelix等智能开发套件,助力参赛队伍应用AI理论工具完成项目开发,解决学科问题。优胜队伍还有机会获得官方获奖证书、飞桨开发者技术专家(PPDE)申请绿色通道、百度飞桨AI基础应用课程、AI for Science应用课程等惊喜福利。
- 报名链接:
https://cas-pra.sugon.com/detail.html?tournament_id=15
相关阅读
- 赛桨PaddleScience Github:
https://github.com/PaddlePaddle/PaddleScience
- 飞桨AI for Science共创计划:
https://www.paddlepaddle.org.cn/science
- 飞桨PPSIG-Science小组:
https://www.paddlepaddle.org.cn/specialgroupdetail?id=9
- AI+Science系列(一):飞桨加速CFD(计算流体力学)原理与实践》:
https://mp.weixin.qq.com/s/pQtyKNOH2g-pyO7AqMuQmw
- 飞桨框架v2.3发布高可复用算子库PHI!重构开发范式,降本增效
https://mp.weixin.qq.com/s/YyBnZBm7rRnllJzwWmb_dA
- 飞桨框架v2.3 API最新升级!对科学计算、概率分布和稀疏Tensor等提供更全面支持!
https://mp.weixin.qq.com/s/XEQkkt2D4wzuaiDXEdQBYw
引用
[1] Argonne National Laboratory. AI for Science Report. (n.d.). Retrieved August 1, 2022, from https://www.anl.gov/ai-for-science-report

关注【飞桨PaddlePaddle】公众号
获取更多技术内容~