[人工智能]【CS231n assignment 2022】Assignment 3 - Part 2，LSTM

🚩前言

• 🐳博客主页：😚睡晚不猿序程😚
• ?首发时间：2022.8.13
• ?最近更新时间：2022.8.13
• 🙆本文由 睡晚不猿序程 原创，首发于 CSDN
• 🤡作者是蒻蒟本蒟，如果文章里有任何错误或者表述不清，请 tt 我，万分感谢！orz

相关文章目录 ：

• 【CS231n assignment 2022】Assignment 2 - Part 1，全连接网络的初始化以及正反向传播
• 【CS231n assignment 2022】Assignment 2 - Part 2，优化器，批归一化以及层归一化
• 【CS231n assignment 2022】Assignment 3 - Part 1，RNN

1. 内容简介

上一次我们完成了基于 RNN 的图片描述网络，RNN 网络有些许的不足，比如长程依赖问题，在这里我们会完成基于 LSTM 的图片描述模型，将会很好的改善这一问题

2. LSTM

在开始做作业之前，先来回顾一下 LSTM 的内容吧

参考资料：LSTM 详解，作者：qian99

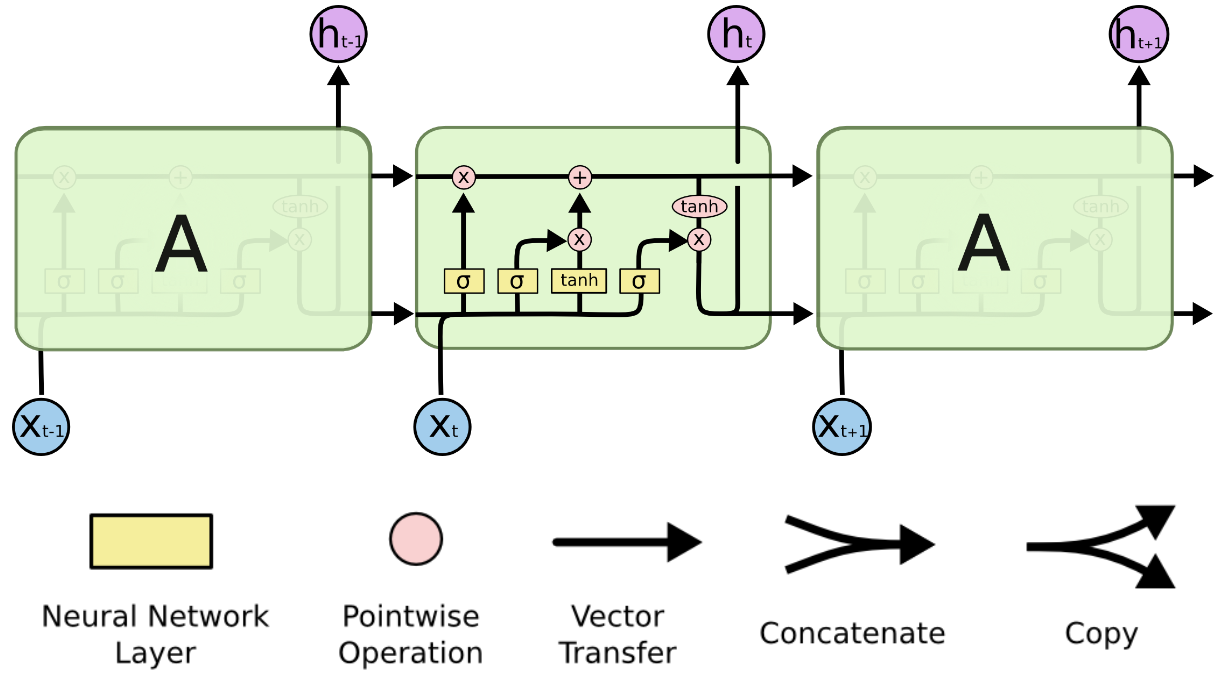
相比于 RNN，LSTM 增加了一个细胞状态（cell state）

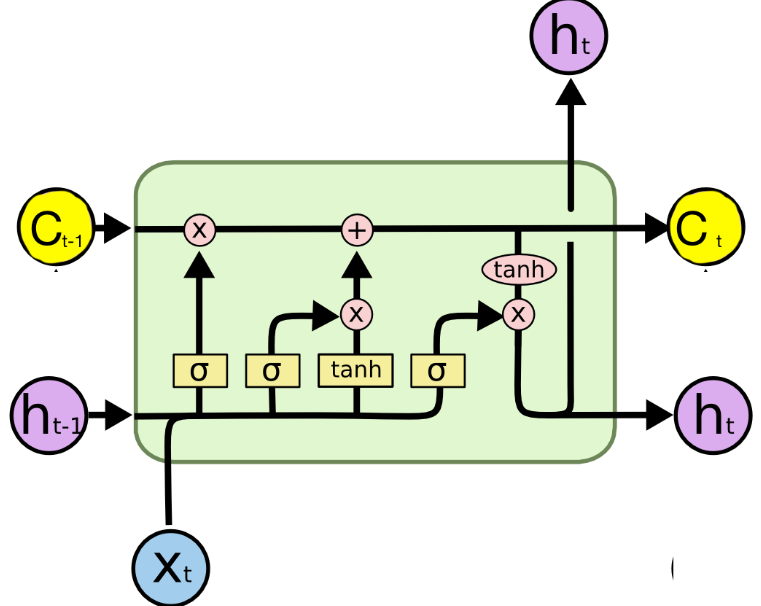
也就是说，对一个一个 LSTM 单元，输入有三个：

• 上一次的隐状态 $h_{t?1}$
• 上一次细胞状态$C_{t?1}$
• 当前输入 $x_t$ ，

输出也有两个：

• 本单元的隐状态 $h_t$
• 本单元的细胞状态$C_t$

我们可以把 LSTM 的传播分为两条线，细胞状态的信息 $C$ 一直只在上面的线上传播

隐状态一直在下面的线上传播，并且他们之间会做交互，LSTM 中包含有三个“门结构”

2.1 LSTM 的输入输出

LSTM 也是 RNN 的一种，所以我们要喂给她一个时序的数据

LSTM 有两个隐藏状态，也就是原先的隐状态和另一个细胞状态，一般初始化为0

2.2 LSTM 的门结构

门，就是被设计出来的一些计算步骤，经过这些计算，来调整输入和两个隐层的值

我们在看一下图，黄色的框框代表一个神经元，也就是一次 $w^{T}x+b$ 的操作，里面的符号是激活函数，分别是 sigmoid 和 tanh

而红色小圈圈代表着按元素计算

2.2.1 遗忘门

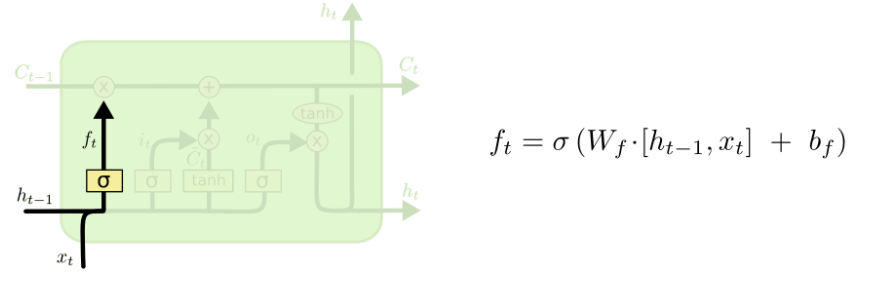
$[h_{t?1},x_t]$：意思是 h 和 x 两个张量进行链接

因为该门输出被限制为（0，1），接下来会和 C 进行按元素乘法，所以 C 中有些信息就会被忘记了（只记住一部分）

因为：只有在乘 1 的情况下，信息才会被完全保留

2.2.2 输入门

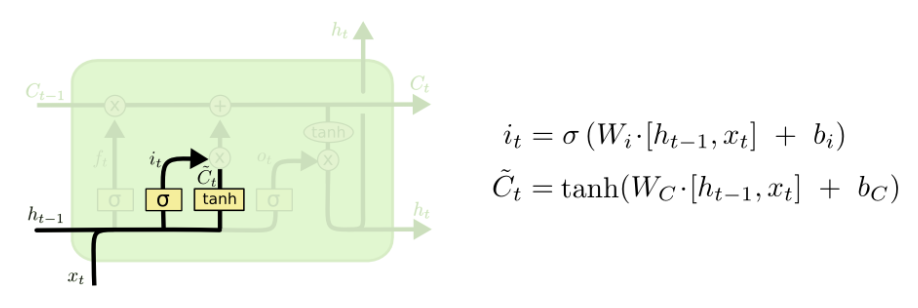
该门由两部分组成：

${\tilde{C}}_t$ ：可以看作是新的输入所带来的信息

$i_t$：和遗忘门的结构一样，所以可以看作是我们要保留多少新的信息

2.2.3 细胞状态更新

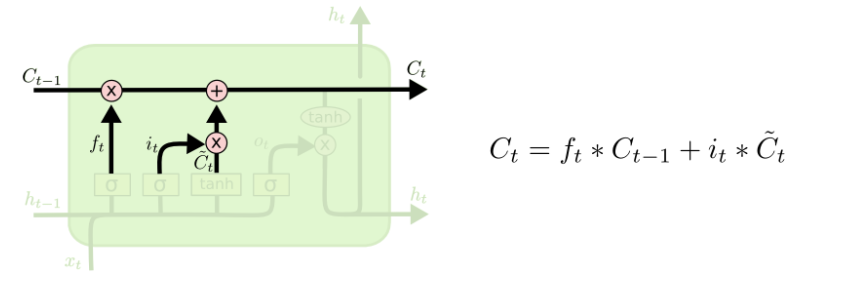
进行细胞状态的更新，也就是我们要忘掉多少以前的信息，记住多少新来的信息，接着两个合成一个当前的新状态，代表当前的全部信息

2.2.4 输出门

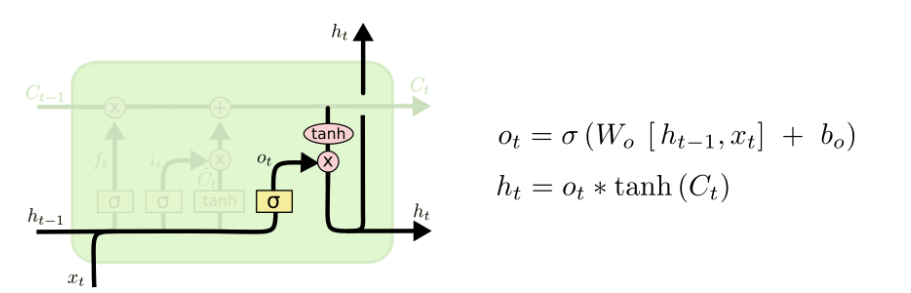
输出门得到的 LSTM 的输出，此时使用的是 $C_t$

我们经过了一个 sigmoid 函数来进行处理，决定输出哪一些内容

$C_t$ 经过了 tanh 的处理，输出范围为（-1，1），然后乘上输出门的结果，就是当前的输出 $h_t$

2.2.5 小总结

所以这里总共有三套参数

• 遗忘门权重，偏置
• 输入门权重，偏置
• ${\tilde{C}}_t$ 计算所需的权重，偏置
• 输出门权重，偏置

所以总共有四套可学习的参数~

3. LSTM for Image Caption

接下来我们要开始做作业了

3.1 LSTM

LSTM RNN 是简单 RNN 的一个常见变种。

简单 RNN 在长序列数据集上进行训练的时候容易出现梯度爆炸和梯度消失，这是多次的矩阵乘法导致的。LSTM 改善了这一问题，它使用“门机制”替代了 RNN 原本的简单更新规则

使用代码实现的时候，我们把上面四个门的权重 W 存储在一个矩阵里面来方便运算

3.1.1 变量

在每一个时间步：

输入：$x_t\in {\mathbb{R}}^D$

先前的隐状态：$h_{t?1}\in {\mathbb{R}}^H$

先前的细胞状态：$c_{t?1}\in {\mathbb{R}}^H$ ，其维度和 h相同

可学习的参数：

1. input-to-hidden 的矩阵：$W_x\in {\mathbb{R}}^{4H\times D}$
2. hidden-to-hidden 的矩阵：$W_h\in {\mathbb{R}}^{4H\times H}$
3. 偏置向量：$b\in {\mathbb{R}}^{4H}$

3.1.2 步骤

在每一个时间步：

1. 计算激活向量$a\in {\mathbb{R}}^{4H}$：$a=W_x{x}_t+W_h{h}_{t?1}+b$

2. 把得到的 $a$ 划分为四个向量： $a_i,a_f,a_o,a_g\in {\mathbb{R}}^H$

3. 分别计算四个门（就是经过激活函数处理）

   1. input gate：i
   2. forget gate：f
   3. output gate：o
   4. block gate：g

4. 进行细胞状态 c 和隐藏状态 h 的更新

   • $c_t=f\odot c_{t?1}+i\odot g$
   • $h_t=o\odot \tanh (c_t)$

代码相关

接下来我们假设：

数据：$X_t\in {\mathbb{R}}^{N\times D}$，$H_t\in {\mathbb{R}}^{N\times H}$

参数：$W_x\in {\mathbb{R}}^{D\times 4H}$, $W_h\in {\mathbb{R}}^{H\times 4H}$

激活状态：$A\in {\mathbb{R}}^{N\times 4H}$，它可以计算的非常快，公式：$A=X_t{W}_x+H_{t?1}{W}_h$

到现在我们可以理清楚在当前作业我们需要做的内容了，现在我们准备开干

3.2 LSTM: Step Forward

我们要完成一个时间步的前向传播

完成文件cs231n/rnn_layers.py 中的lstm_step_forward 函数，它将会和rnn的相似

有了上面的铺垫，做前向传播应该很容易，我们直接来看代码

def lstm_step_forward(x, prev_h, prev_c, Wx, Wh, b):
    """Forward pass for a single timestep of an LSTM.

    The input data has dimension D, the hidden state has dimension H, and we use
    a minibatch size of N.
    输入数据维度 D，隐状态维度 H，minibatch 大小为N

    Note that a sigmoid() function has already been provided for you in this file.

    Inputs:
    - x: Input data, of shape (N, D)
    - prev_h: Previous hidden state, of shape (N, H)
    - prev_c: previous cell state, of shape (N, H)
    - Wx: Input-to-hidden weights, of shape (D, 4H)
    - Wh: Hidden-to-hidden weights, of shape (H, 4H)
    - b: Biases, of shape (4H,)

    Returns a tuple of:
    - next_h: Next hidden state, of shape (N, H)
    - next_c: Next cell state, of shape (N, H)
    - cache: Tuple of values needed for backward pass.
    """
    next_h, next_c, cache = None, None, None
    #############################################################################
    # TODO: Implement the forward pass for a single timestep of an LSTM.        #
    # You may want to use the numerically stable sigmoid implementation above.  #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    H = prev_h.shape[1]
    a = x.dot(Wx)+prev_h.dot(Wh)+b   # (N,4H)

    input_gate = a[:, 0:H]
    forget_gate = a[:, H:2*H]
    output_gate = a[:, 2*H:3*H]
    block_gate = a[:, 3*H:4*H]

    i = sigmoid(input_gate)
    f = sigmoid(forget_gate)
    o = sigmoid(output_gate)
    c = np.tanh(block_gate)

    c_forgot = prev_c*f
    c_input = c*i
    next_c = c_forgot+c_input

    next_h = o*np.tanh(next_c)
    
	cache = (x, Wx, Wh, a, prev_c, prev_h, next_c)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ##############################################################################
    #                               END OF YOUR CODE                             #
    ##############################################################################

    return next_h, next_c, cache

代码详解

• 上面的讲解是将输入和隐藏状态拼接起来再进行矩阵运算，而这里选择的是分开计算，两个效果相同

3.3 LSTM: Step Backward

在这里我们要实现反向传播

根据上面的前向传播我们可以看出，这里的计算大部分都是矩阵的按元素运算，所以反向传播就是把梯度从后往前算一下就可以啦，也就是前向传播的逆过程。但是我们先注意一下 sigmoid 函数和 tanh 的求导公式：
$$\begin{gathered} \frac{?\sigma }{?x}=\sigma (x)(1?\sigma (x)) \\ \frac{?tanh}{?x}=1?tan{h}^2(x) \end{gathered}$$
了解了公式我们就可以进行反向传播了

def lstm_step_backward(dnext_h, dnext_c, cache):
    """Backward pass for a single timestep of an LSTM.

    Inputs:
    - dnext_h: Gradients of next hidden state, of shape (N, H)
    - dnext_c: Gradients of next cell state, of shape (N, H)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient of input data, of shape (N, D)
    - dprev_h: Gradient of previous hidden state, of shape (N, H)
    - dprev_c: Gradient of previous cell state, of shape (N, H)
    - dWx: Gradient of input-to-hidden weights, of shape (D, 4H)
    - dWh: Gradient of hidden-to-hidden weights, of shape (H, 4H)
    - db: Gradient of biases, of shape (4H,)
    """
    dx, dprev_h, dprev_c, dWx, dWh, db = None, None, None, None, None, None
    #############################################################################
    # TODO: Implement the backward pass for a single timestep of an LSTM.       #
    #                                                                           #
    # HINT: For sigmoid and tanh you can compute local derivatives in terms of  #
    # the output value from the nonlinearity.                                   #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    x, Wx, Wh, a, prev_c, prev_h, next_c = cache
    H = prev_c.shape[1]
    input_gate = a[:, 0:H]
    forget_gate = a[:, H:2*H]
    output_gate = a[:, 2*H:3*H]
    block_gate = a[:, 3*H:4*H]

    i = sigmoid(input_gate)
    f = sigmoid(forget_gate)
    o = sigmoid(output_gate)
    c = np.tanh(block_gate)

    do = dnext_h*np.tanh(next_c)

    dnext_c += dnext_h * o * (1 - np.tanh(next_c)**2)

    dc_forgot = dnext_c
    dc_input = dnext_c

    dc = i*dc_input
    di = c*dc_input

    dprev_c = f*dc_forgot
    df = prev_c*dc_forgot

    da = np.zeros_like(a)
    da[:, 0:H] = i*(1-i)*di
    da[:, H:2*H] = f*(1-f)*df
    da[:, 2*H:3*H] = o*(1-o)*do		# 上面三个为sigmoid 求导
    da[:, 3*H:4*H] = (1-c**2)*dc	# tanh求导

    dx = da.dot(Wx.T)
    dprev_h = da.dot(Wh.T)
    dWx = x.T.dot(da)
    dWh = prev_h.T.dot(da)
    db = np.sum(da, axis=0)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ##############################################################################
    #                               END OF YOUR CODE                             #
    ##############################################################################

    return dx, dprev_h, dprev_c, dWx, dWh, db

代码详解

• 这次的反向传播比较简单，我们从后往前计算梯度就可以了
• 注意dnext_c 的问题，其梯度有两个输入，所以要进行 += 运算

3.4 LSTM: Forward

接下来我们会完成 LSTM 的前向传播步骤啦，我们会用到我们之前构造的 stepforward 函数

因为比较简单，我们直接来看代码

def lstm_forward(x, h0, Wx, Wh, b):
    """Forward pass for an LSTM over an entire sequence of data.

    We assume an input sequence composed of T vectors, each of dimension D. The LSTM uses a hidden
    size of H, and we work over a minibatch containing N sequences. After running the LSTM forward,
    we return the hidden states for all timesteps.
    一句话 T 个词语，
    每个词维度为 D
    隐状态维度 H
    minibatch 大小为 N
    经过 LSTM 处理，返回每个时间片的隐状态

    Note that the initial cell state is passed as input, but the initial cell state is set to zero.
    Also note that the cell state is not returned; it is an internal variable to the LSTM and is not
    accessed from outside.
    初始的细胞状态被置为0
    细胞状态不会返回，细胞状态属于 LSTM 的内部变量，不是通过外部得到的

    Inputs:
    - x: Input data of shape (N, T, D)
    - h0: Initial hidden state of shape (N, H)
    - Wx: Weights for input-to-hidden connections, of shape (D, 4H)
    - Wh: Weights for hidden-to-hidden connections, of shape (H, 4H)
    - b: Biases of shape (4H,)

    Returns a tuple of:
    - h: Hidden states for all timesteps of all sequences, of shape (N, T, H)
    - cache: Values needed for the backward pass.
    """
    h, cache = None, None
    #############################################################################
    # TODO: Implement the forward pass for an LSTM over an entire timeseries.   #
    # You should use the lstm_step_forward function that you just defined.      #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    N, T, D = x.shape
    H = h0.shape[1]

    h = np.zeros((N, T, H))
    c = np.zeros((N, T, H))
    c0 = np.zeros_like(h0)
    cache = []
    for i in range(T):
        if i == 0:
            h[:, i, :], c[:, i, :], forward_cache = lstm_step_forward(
                x[:, i, :], h0, c0, Wx, Wh, b)
        else:
            h[:, i, :], c[:, i, :], forward_cache = lstm_step_forward(
                x[:, i, :], h[:, i-1, :], c[:, i-1, :], Wx, Wh, b)
        cache.append(forward_cache)

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        ##############################################################################
        #                               END OF YOUR CODE                             #
        ##############################################################################

    return h, cache

代码详解

• c 是一个内部状态（细胞状态），我们同样也要给他构造一个张量来进行保存
• c0 代表 c 的初始状态，初始化为全0

3.5 LSTM: backward

在这里我们会完成 LSTM 的反向传播算法，LSTM 的反向传播算法和 RNN 的反向传播算法类似，只需要把单步反向传播的函数更换一下就可以了，现在我们来看看代码

def lstm_backward(dh, cache):
    """Backward pass for an LSTM over an entire sequence of data.

    Inputs:
    - dh: Upstream gradients of hidden states, of shape (N, T, H)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient of input data of shape (N, T, D)
    - dh0: Gradient of initial hidden state of shape (N, H)
    - dWx: Gradient of input-to-hidden weight matrix of shape (D, 4H)
    - dWh: Gradient of hidden-to-hidden weight matrix of shape (H, 4H)
    - db: Gradient of biases, of shape (4H,)
    """
    dx, dh0, dWx, dWh, db = None, None, None, None, None
    #############################################################################
    # TODO: Implement the backward pass for an LSTM over an entire timeseries.  #
    # You should use the lstm_step_backward function that you just defined.     #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    N, T, H = dh.shape
    D = cache[0][0].shape[1]

    dx = np.zeros((N, T, D))
    dh0 = np.zeros((N, H))
    dh_i = np.zeros((N, H))
    dWx = np.zeros((D, 4*H))
    dWh = np.zeros((H, 4*H))
    db = np.zeros((4*H))
    dc_i = np.zeros_like(dh_i)
    for i in range(T-1, -1, -1):
        dh_i += dh[:, i, :]
        dx_i, dh_i, dc_i, dWx_i, dWh_i, db_i = lstm_step_backward(
            dh_i, dc_i, cache[i])
        dx[:, i, :] = dx_i
        dWx += dWx_i
        dWh += dWh_i
        db += db_i
    dh0 = dh_i

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ##############################################################################
    #                               END OF YOUR CODE                             #
    ##############################################################################

    return dx, dh0, dWx, dWh, db

代码详解

• 关于细胞状态的梯度 dc_i
  • 反向传播是从后往前，因为细胞状态并没有输出，所以初始梯度应该是一个全零的向量
• dh_i 是 += 进行赋值，因为反向传播的梯度有两个方向，和 RNN 一样，一个是“上方”传递过来的梯度，另一个是从“右边”传递过来的梯度
  • 同时 dh_i 初始也为0，因为刚开始只有“上方”传递过来的梯度，没有“右边”传递过来的梯度

3.6 LSTM Captioning Model

现在我们已经完成了 LSTM，接下来我们要在完善一下文件cs231n/classifiers/rrn.py 中CaptioningRNN中的loss函数，也就是把 LSTM 添加进去

只需要把 LSTM 的前向传播和反向传播添加进去就可以啦，添加的代码分别是：

# 使用RNN进行前向传播(随着时间，也就是“向右”)
if self.cell_type == "rnn":
    hidden_state, hidden_cache = rnn_forward(
        word_emb_in, ini_hidden_state, Wx, Wh, b)
else:
    hidden_state, hidden_cache = lstm_forward(
        word_emb_in, ini_hidden_state, Wx, Wh, b)

# 反向传播
dout, grads["W_vocab"], grads["b_vocab"] = temporal_affine_backward(
    dtemp_out, temp_cache)

if self.cell_type == "rnn":
    demb, dini_hidden, grads["Wx"], grads["Wh"], grads["b"] = rnn_backward(
        dout, hidden_cache)
else:
    demb, dini_hidden, grads["Wx"], grads["Wh"], grads["b"] = lstm_backward(
        dout, hidden_cache)

好了我们直接放出完整的代码，代码如下

    def loss(self, features, captions):
        """
        Compute training-time loss for the RNN. We input image features and
        ground-truth captions for those images, and use an RNN (or LSTM) to compute
        loss and gradients on all parameters.

        Inputs:
        - features: Input image features, of shape (N, D)
        - captions: Ground-truth captions; an integer array of shape (N, T + 1) where
          each element is in the range 0 <= y[i, t] < V

        Returns a tuple of:
        - loss: Scalar loss
        - grads: Dictionary of gradients parallel to self.params
        """
        # Cut captions into two pieces: captions_in has everything but the last word
        # and will be input to the RNN; captions_out has everything but the first
        # word and this is what we will expect the RNN to generate. These are offset
        # by one relative to each other because the RNN should produce word (t+1)
        # after receiving word t. The first element of captions_in will be the START
        # token, and the first element of captions_out will be the first word.
        # 把描述分为两个部分，captions_in不包含最后一个词，将会输入进入RNN
        # caption_out 不包含第一个词，是我们希望RNN生成的内容
        # 为何彼此偏移一个的原因是 RNN 应该在接收到 t 个单词后生成 t+1 个单词
        # caption_in 的第一个元素是 <start>
        # caption_out 的第一个元素是第一个单词

        captions_in = captions[:, :-1]
        captions_out = captions[:, 1:]

        # You'll need this
        mask = captions_out != self._null

        # Weight and bias for the affine transform from image features to initial
        # hidden state
        # 把图片特征转化成隐藏状态的全连接网路
        W_proj, b_proj = self.params["W_proj"], self.params["b_proj"]

        # Word embedding matrix
        # 词嵌入矩阵
        W_embed = self.params["W_embed"]

        # Input-to-hidden, hidden-to-hidden, and biases for the RNN
        Wx, Wh, b = self.params["Wx"], self.params["Wh"], self.params["b"]

        # Weight and bias for the hidden-to-vocab transformation.
        W_vocab, b_vocab = self.params["W_vocab"], self.params["b_vocab"]

        loss, grads = 0.0, {}
        ############################################################################
        # TODO: Implement the forward and backward passes for the CaptioningRNN.   #
        # In the forward pass you will need to do the following:                   #
        # (1) Use an affine transformation to compute the initial hidden state     #
        #     from the image features. This should produce an array of shape (N, H)#
        # (2) Use a word embedding layer to transform the words in captions_in     #
        #     from indices to vectors, giving an array of shape (N, T, W).         #
        # (3) Use either a vanilla RNN or LSTM (depending on self.cell_type) to    #
        #     process the sequence of input word vectors and produce hidden state  #
        #     vectors for all timesteps, producing an array of shape (N, T, H).    #
        # (4) Use a (temporal) affine transformation to compute scores over the    #
        #     vocabulary at every timestep using the hidden states, giving an      #
        #     array of shape (N, T, V).                                            #
        # (5) Use (temporal) softmax to compute loss using captions_out, ignoring  #
        #     the points where the output word is <NULL> using the mask above.     #
        #                                                                          #
        #                                                                          #
        # Do not worry about regularizing the weights or their gradients!          #
        #                                                                          #
        # In the backward pass you will need to compute the gradient of the loss   #
        # with respect to all model parameters. Use the loss and grads variables   #
        # defined above to store loss and gradients; grads[k] should give the      #
        # gradients for self.params[k].                                            #
        #                                                                          #
        # Note also that you are allowed to make use of functions from layers.py   #
        # in your implementation, if needed.                                       #
        ############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # 前向传播
        # 构建初始状态（通过输入的图片进行运算）
        ini_hidden_state, ini_cache = affine_forward(features, W_proj, b_proj)

        # 进行词嵌入（把输入转化成词向量表示）
        word_emb_in, word_emb_cache = word_embedding_forward(
            captions_in, W_embed)

        # 使用RNN进行前向传播(随着时间，也就是“向右”)
        if self.cell_type == "rnn":
            hidden_state, hidden_cache = rnn_forward(
                word_emb_in, ini_hidden_state, Wx, Wh, b)
        else:
            hidden_state, hidden_cache = lstm_forward(
                word_emb_in, ini_hidden_state, Wx, Wh, b)

        # 求出每个时间节点的输出（也就是“向上”）
        temp_out, temp_cache = temporal_affine_forward(
            hidden_state, W_vocab, b_vocab)

        # 求出每个时间节点的损失
        loss, dtemp_out = temporal_softmax_loss(temp_out, captions_out, mask)

        # 反向传播
        dout, grads["W_vocab"], grads["b_vocab"] = temporal_affine_backward(
            dtemp_out, temp_cache)

        if self.cell_type == "rnn":
            demb, dini_hidden, grads["Wx"], grads["Wh"], grads["b"] = rnn_backward(
                dout, hidden_cache)
        else:
            demb, dini_hidden, grads["Wx"], grads["Wh"], grads["b"] = lstm_backward(
                dout, hidden_cache)

        grads["W_embed"] = word_embedding_backward(demb, word_emb_cache)

        dfeatures, grads["W_proj"], grads["b_proj"] = affine_backward(
            dini_hidden, ini_cache)

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

        return loss, grads

3.7 Overfit LSTM Captioning Model on Small Data

在这里我们会用一个小数据集来让 LSTM 过拟合，经过测试，总损失应该会低于0.5

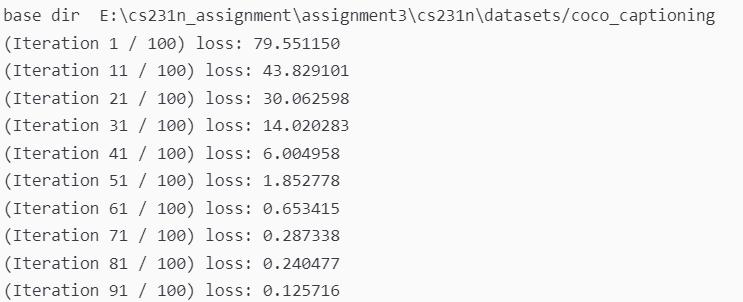
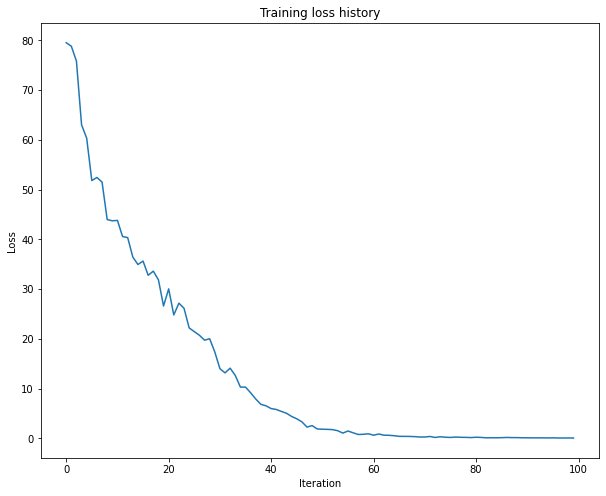
最后输出一下总损失：

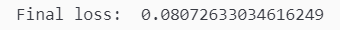
总损失仅为 0.08，非常低！

3.8 LSTM Sampling at Test Time

接下来我们要用 LSTM 来进行图像描述了，我们需要稍微修改一下sample函数来使用 LSTM，和上面的修改一样，只需要添加一个if就行了，我们直接来看完整代码

    def sample(self, features, max_length=30):
        """
        Run a test-time forward pass for the model, sampling captions for input
        feature vectors.

        At each timestep, we embed the current word, pass it and the previous hidden
        state to the RNN to get the next hidden state, use the hidden state to get
        scores for all vocab words, and choose the word with the highest score as
        the next word. The initial hidden state is computed by applying an affine
        transform to the input image features, and the initial word is the <START>
        token.
        每一个时间步，进行词嵌入，并进行前向传播的到当前的隐藏状态
        用隐藏状态来得到单词的分数，选择分数最高的作为接下来的词
        初始的隐藏状态使用输入图像做线性变换来得到
        初始的词语为<START> token


        For LSTMs you will also have to keep track of the cell state; in that case
        the initial cell state should be zero.

        Inputs:
        - features: Array of input image features of shape (N, D).
        - max_length: Maximum length T of generated captions.

        Returns:
        - captions: Array of shape (N, max_length) giving sampled captions,
          where each element is an integer in the range [0, V). The first element
          of captions should be the first sampled word, not the <START> token.
        """
        N = features.shape[0]
        captions = self._null * np.ones((N, max_length), dtype=np.int32)

        # Unpack parameters
        W_proj, b_proj = self.params["W_proj"], self.params["b_proj"]
        W_embed = self.params["W_embed"]
        Wx, Wh, b = self.params["Wx"], self.params["Wh"], self.params["b"]
        W_vocab, b_vocab = self.params["W_vocab"], self.params["b_vocab"]

        ###########################################################################
        # TODO: Implement test-time sampling for the model. You will need to      #
        # initialize the hidden state of the RNN by applying the learned affine   #
        # transform to the input image features. The first word that you feed to  #
        # the RNN should be the <START> token; its value is stored in the         #
        # variable self._start. At each timestep you will need to do to:          #
        # (1) Embed the previous word using the learned word embeddings           #
        # (2) Make an RNN step using the previous hidden state and the embedded   #
        #     current word to get the next hidden state.                          #
        # (3) Apply the learned affine transformation to the next hidden state to #
        #     get scores for all words in the vocabulary                          #
        # (4) Select the word with the highest score as the next word, writing it #
        #     (the word index) to the appropriate slot in the captions variable   #
        #                                                                         #
        # For simplicity, you do not need to stop generating after an <END> token #
        # is sampled, but you can if you want to.                                 #
        #                                                                         #
        # HINT: You will not be able to use the rnn_forward or lstm_forward       #
        # functions; you'll need to call rnn_step_forward or lstm_step_forward in #
        # a loop.                                                                 #
        #                                                                         #
        # NOTE: we are still working over minibatches in this function. Also if   #
        # you are using an LSTM, initialize the first cell state to zeros.        #
        ###########################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        hidden_state, _ = affine_forward(features, W_proj, b_proj)
        word = self._start*np.ones(N, dtype=np.int32)  # (N,)
        for i in range(max_length):
            word_embed, _ = word_embedding_forward(word, W_embed)
            if self.cell_type == "rnn":
                hidden_state, _ = rnn_step_forward(
                    word_embed, hidden_state, Wx, Wh, b)
            else:
                hidden_state, _ = lstm_step_forward(
                    word_embed, hidden_state, Wx, Wh, b)
            scores, _ = affine_forward(hidden_state, W_vocab, b_vocab)
            word = np.argmax(scores, axis=1)
            captions[:, i] = word
        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################
        return captions

接下来我们就可以验证一下了

因为我是在windows下运行，所以对验证代码做如下修改：

# If you get an error, the URL just no longer exists, so don't worry!
# You can re-sample as many times as you want.
for split in ['train', 'val']:
    minibatch = sample_coco_minibatch(small_data, split=split, batch_size=2)
    gt_captions, features, urls = minibatch
    gt_captions = decode_captions(gt_captions, data['idx_to_word'])

    sample_captions = small_lstm_model.sample(features)
    sample_captions = decode_captions(sample_captions, data['idx_to_word'])

    for gt_caption, sample_caption, url in zip(gt_captions, sample_captions, urls):
        # img = image_from_url(url)
        # Skip missing URLs.
        # if img is None: continue
        # plt.imshow(img) 	上面这些全部注释掉
        print(url)	# 输出图像的 url
        plt.title('%s\n%s\nGT:%s' % (split, sample_caption, gt_caption))
        plt.axis('off')
        plt.show()

然后就可以进行验证了，但是看起来这个模型不是很聪明的样子

这描述的是一个东西吗？是不是少了个 hot 呀？

3. 总结、预告

在这次作业中，我们成功的使用了 numpy 实现了 LSTM

欸那有一个问题，之前作业二的剩余部分怎么就不见了呢？

呜呜呜拖拉博主马上会补上来的！对不起大家呜呜呜