目录
前言
????????今天我们要分享的论文是《Deep Residual Learning for Image Recognition》,大名鼎鼎的残差网络。这篇论文主要是提出了一种残差结构,来解决训练深度网络会存在的网络退化问题。
为何残差
????????今天和往常不一样,我们先来说说为啥要用到残差结构。众所周知(我们前几篇也有提到过),深度对于一个网络来说大有裨益,提高深度就代表提高性能。但实际上,随着网络深度的提高,也会随之出现各种问题。最主要的问题有两个,其一是梯度消失问题,这个通过归一化初始化和中间层归一化能够解决。第二个问题就是网络退化的问题。
????????这篇文章的作者通过实验发现,更深的网络的测试和训练误差比浅层网络的要大,如下图。
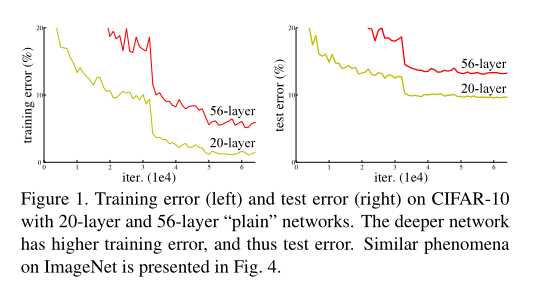
图片来自论文
????????其中红色是56层网络,而黄色是20层网络。可以看到,随着迭代次数的增加,无论是训练误差还是测试误差,56层网络的误差始终比20层网络的要大。
????????作者提出这是一种网络退化的问题,也就是网络随着深度增加,性能会逐渐饱和,然后深度再提高时,性能就会飞速下降。
????????但其实这是不符合我们的常识的,我们一直认为,网络越深,性能越好。纵使性能趋于饱和,它最多就是保持不变,怎么可能会下降呢?
????????我通过总结论文和其他相关资料,尝试给出一个我理解到的解释:理论上当我们在某一层已经获得了最优的效果,那么下一层无法再精进,就只能是上一层的恒等式。比如说第19层最优了,那么第20层的结果就应该是第19层的结果乘1,相当于做一个简单的线性变换。但实际情况是网络退化了,所以我们可以合情推理:网络拟合一个恒等式不容易。
????????至于为啥拟合恒等式不容易,有一说法是两层之间夹着非线性激活函数,比较难拟合这种线性变换。原文也提到:“退化问题表明,解算器可能难以通过多个非线性层近似单位映射。”
何为残差
????????知道了网络退化的原因,论文作者就开始设计一种新的结构:残差结构。如果说我们以前学习的是从x到y的映射规律,那么残差学习的就是x与y的差的规律。
????????用数学语言表示就是:我们原本学习的是y=f(x)中的f,但是f在深层比较难学,所以我们转而学习y=H(x)+x中的H,当我们学会H后,算出H(x),再加上x,就能得到y了嘛。
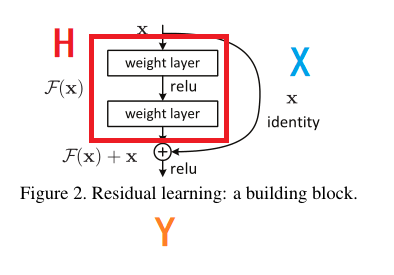
图片改自论文
????????就像这个图,中间这部分就是用来拟合我们刚才说的H,然后x从旁边走捷径到H的结果这,加起来。
????????两者的结果看起来貌似一样,但实际效果却是不一样的。使用残差结构后,我们学习到的实际是输入和输出之间的差值。假设我们的输入是100,然后输出是101。一般来说我们初始化权重都为0,是从0到1容易还是从0到101容易呢?很显然是从0到1容易。
????????而且我们在使用BP算法时,要计算梯度。以前的方法是:y’=f’(x),现在残差是y’=H’(x)+1。如果f’(x)很小,那么拟合就比较难了,如果H’(x)比较小,我们还有后面的1在撑场面,梯度不会太小,更好进行优化。
????????我们再讲通俗一点:前面的比较浅的层学习主要负责比较粗糙的拟合,而越深的层呢,负责一些精细的微调。残差相当于有了个先验,再去拟合这个扰动,所以可能会更容易拟合。(这是我个人对残差的理解)
残差结构细节
????????我们再看这个图:
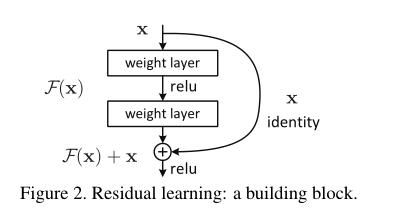
图片来自论文
????????我们使用这个结构时,要注意一点,那就是输出要和输入的维度一样(不一样的处理我们后面再说),也就是尺寸和通道要一致。我们要如何操作才能保持一致呢?
????????首先x走的这条旁边小路是不会有维度的改变的,所以主要是中间堆积的几个层。这里我们就可以用VGG网络的思路了,像我们之前这篇里写的一样,我们可以堆积3*3卷积核、步长和padding为1的卷积层。论文作者说,这里面可以堆积多层,但如果只有一层,就相当于一个线性变换,暂时还没看出它的优势在哪里。
????????那假如输入和输出维度不一样那该怎么办呢?输入和输出维度不一样一般是中间堆积的层改变了维度,和输入的x不一样了,导致加不起来。所以我们可以将x的维度改成和中间堆积层的结果一致。论文里提出了两种方法。
????????首先是通道不够就用padding来解决,我的理解是如下图:
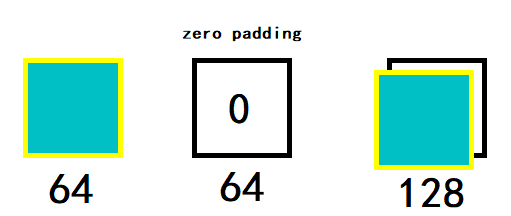
????????其次是我们可以使用1*1卷积。也就是那个扫描的区域只有1*1的大小,相当于用相同的权重给每一个像素做线性变换。比如说,我们的输入是14*14*128,我们可以使用256个1*1*128的卷积核,采取步长为1,padding为0的卷积,就能得到14*14*256的输出。不懂为何的可以看我之前写的这篇,这里就不再赘述了。
????????经过实验对比,方法一不会增加新的参数,方法二虽然增加了新的参数(1*1卷积的权重),但效果会比方法一好一点。
????????残差块除了这种结构之外,还有另外一种。
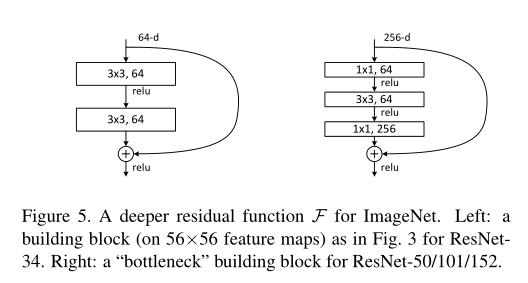
图片来自论文
????????上图中左边是我们刚才讲的一种,右边是另外一种残差块,也叫“瓶颈”。因为它先从高通道转为低通道(256变为64),然后又从低通道变为高通道(64变为256)。就像瓶颈一样,中间忽然窄了。这种结构用于ResNet的50层/101层/152层的配置中。
网络结构
????????说完残差块的细节,我们再看看ResNet的网络结构。
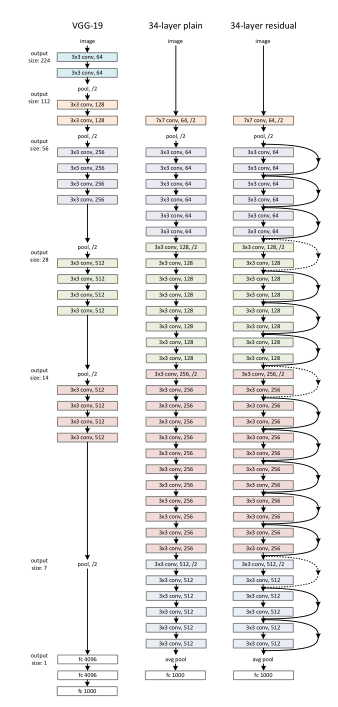
图片来自论文
????????ResNet有很多配置,最高能去到1202层,我们这里就拿最经典的34层来讲。34层的结构其实是在VGG-16的网络结构基础上改进来的。上图左边是VGG、中间是改进的网络结构,右边是中间的结构加上残差连接,所以右边才算是ResNet,中间是还没加工过的。大家可以根据我们上述的内容猜猜中三个网络的性能孰强孰弱。答案是右边最强,左边次之,中间最弱。因为中间的层数增加导致网络退化,而右边的使用了残差,发挥了深层的优势。
????????补充:图中右边的箭头,实线为相同维度的连接,虚线为不同维度的连接。
????????但其实你看这个图是不知道如何去计算的,但里面的计算大部分都是类似的,我们举一两个例子给大家。
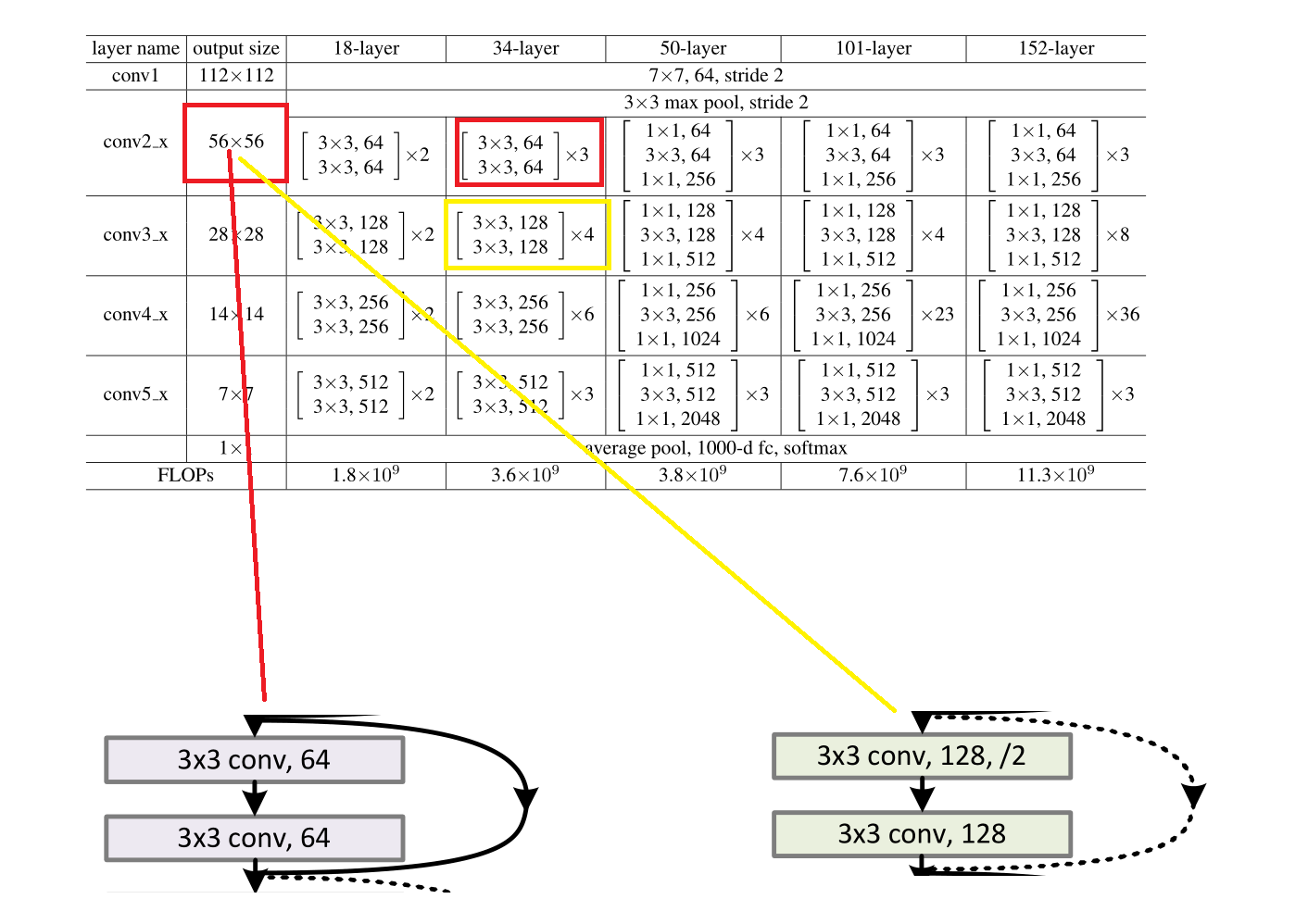
图片改自论文
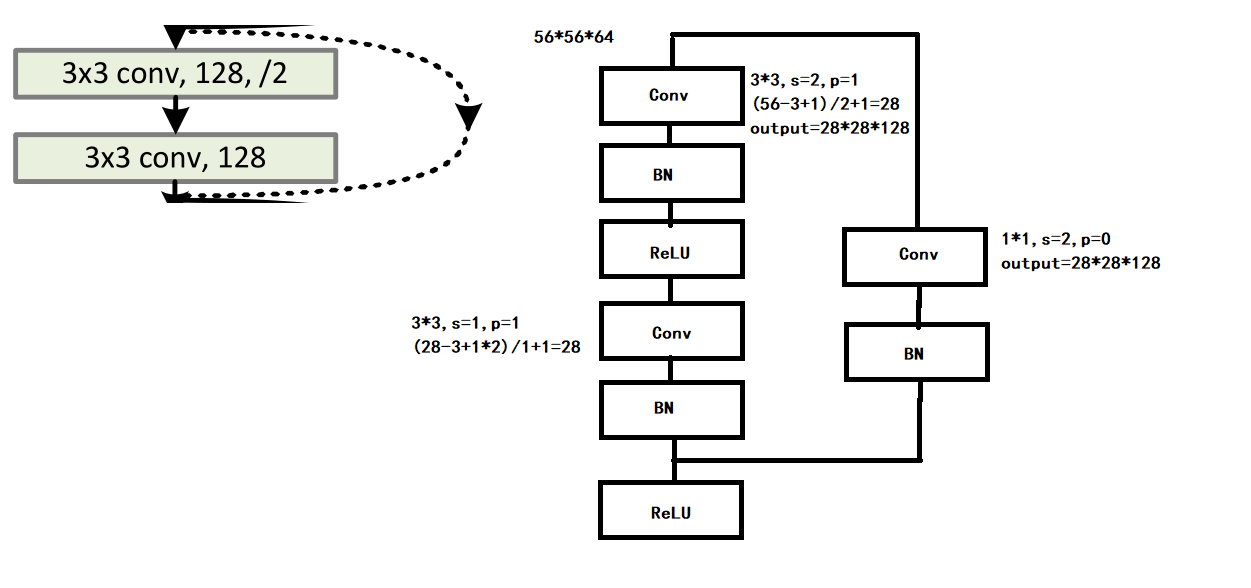
????????我们选取这两个例子,一个是实线的,一个是虚线的。我们再根据官方的这个表,可以得出两个的输入都是56*56*64。
????????首先我们先把他们的结构补全,根据官方的说法:“我们在每次卷积之后和激活之前采用批量归一化(BN)”,所以他们的正确结构应该是下图,同时实线与虚线的计算也在图中了。
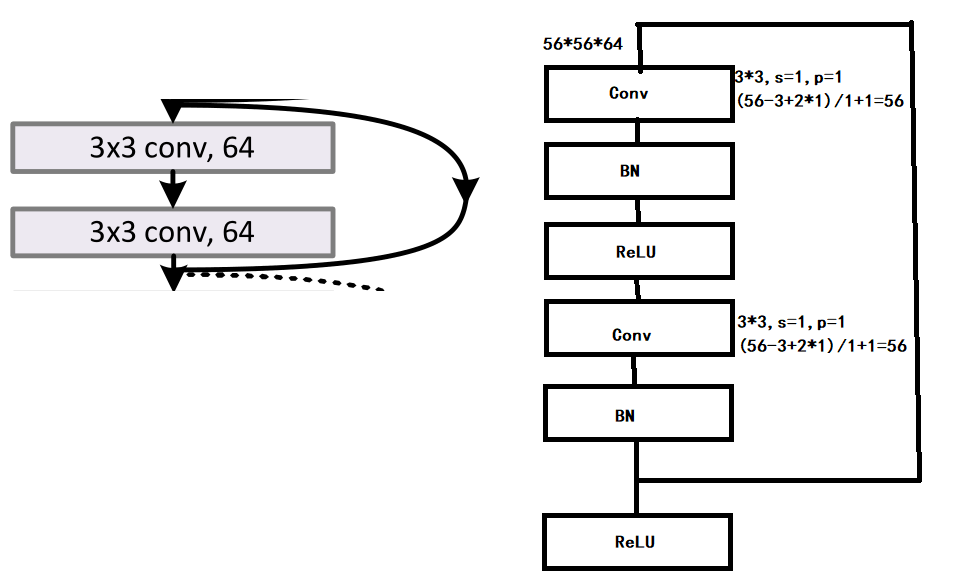
Pytorch实现
????????下面我们再进行Pytorch的实现,实现一下ResNet-34。
# 相关引入
import torch.nn as nn
import torch
# 残差块类
class ResidualBlock(nn.Module):
def __init__(self,in_channels,out_channels,stride,dotted_flag=False):
super(ResidualBlock,self).__init__()
self.conv1=nn.Conv2d(in_channels=in_channels,out_channels=out_channels,kernel_size=3,stride=stride,padding=1)
self.bn1=nn.BatchNorm2d(out_channels)
self.relu = nn.ReLU(inplace=True)
self.conv2 = nn.Conv2d(in_channels=out_channels, out_channels=out_channels, kernel_size=3, stride=1,padding=1)
self.bn2 = nn.BatchNorm2d(out_channels)
self.dotted_flag=dotted_flag
self.downsample=None
# 如果是虚线,则定义旁边那条路x的1*1卷积下采样
if self.dotted_flag:
self.downsample = nn.Sequential(
nn.Conv2d(in_channels=in_channels,out_channels=out_channels, kernel_size=1, stride=stride),
nn.BatchNorm2d(out_channels)
)
def forward(self, x):
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
if self.downsample is not None:
x = self.downsample(x)
out += x
out = self.relu(out)
return out
# 定义网络
class ResNet(nn.Module):
def __init__(self):
super(ResNet, self).__init__()
self.conv1=nn.Conv2d(in_channels=3,out_channels=64,kernel_size=7,stride=2,padding=3)
self.pool=nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
self.layer1=self.make_layer(3,64,64)
self.layer2=self.make_layer(4,64,128,True)
self.layer3 = self.make_layer(6, 128, 256,True)
self.layer4 = self.make_layer(3, 256, 512,True)
self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(512, 1000)
# 堆积残差块
def make_layer(self,num,in_channels,out_channels,dotted_flag=False):
layer=[]
for i in range(num):
if dotted_flag and i==0:
layer.append(ResidualBlock(in_channels,out_channels,2,True))
continue
layer.append(ResidualBlock(out_channels, out_channels, 1))
return nn.Sequential(*layer)
def forward(self,x):
out=self.conv1(x) # output [64,112,112]
out=self.pool(out) # output [64,56,56]
out=self.layer1(out) # output [64,56,56]
out=self.layer2(out) # output [128,28,28]
out=self.layer3(out) # output [256,14,14]
out=self.layer4(out) # output [512,7,7]
out=self.avgpool(out) # output [512,1,1]
out=torch.flatten(out, 1) # output [batch,512]
out=self.fc(out) # output [batch,1000]
return out结果讨论
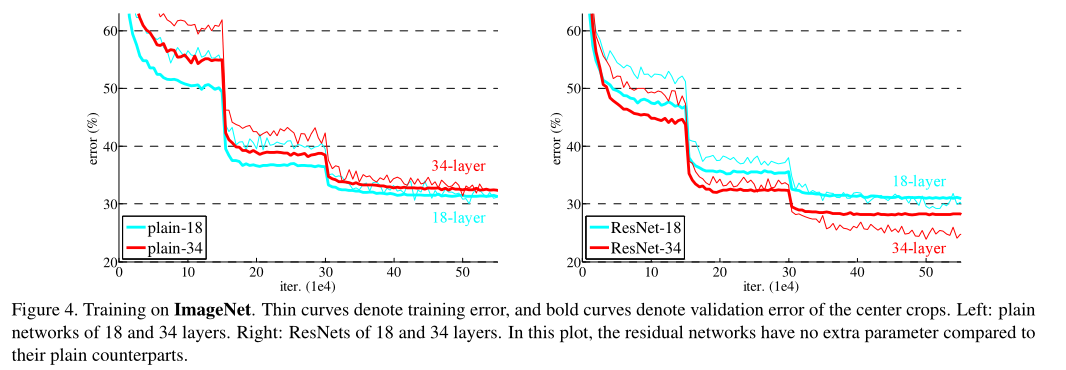
????????讨论完网络结构,我们再讨论一下使用了残差的结果。先看这个图:
图片来自论文
????????左边是没有使用残差,右边是使用了残差。而细线是训练误差,实线是测试误差。可以看到没有使用残差时是浅层效果好,而实现残差后,是深层的效果好。
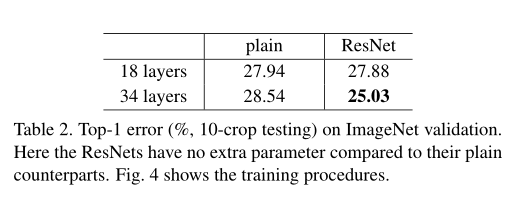
图片来自论文
????????再看具体的数据,可以看出使用了残差可以使浅层和深层的效果都提升,而因为使用了残差后,34层发挥了深层优势,所以误差最小。
作者:公|众|号【荣仙翁】
内容同步在其中,想看更多内容可以关注我哦。