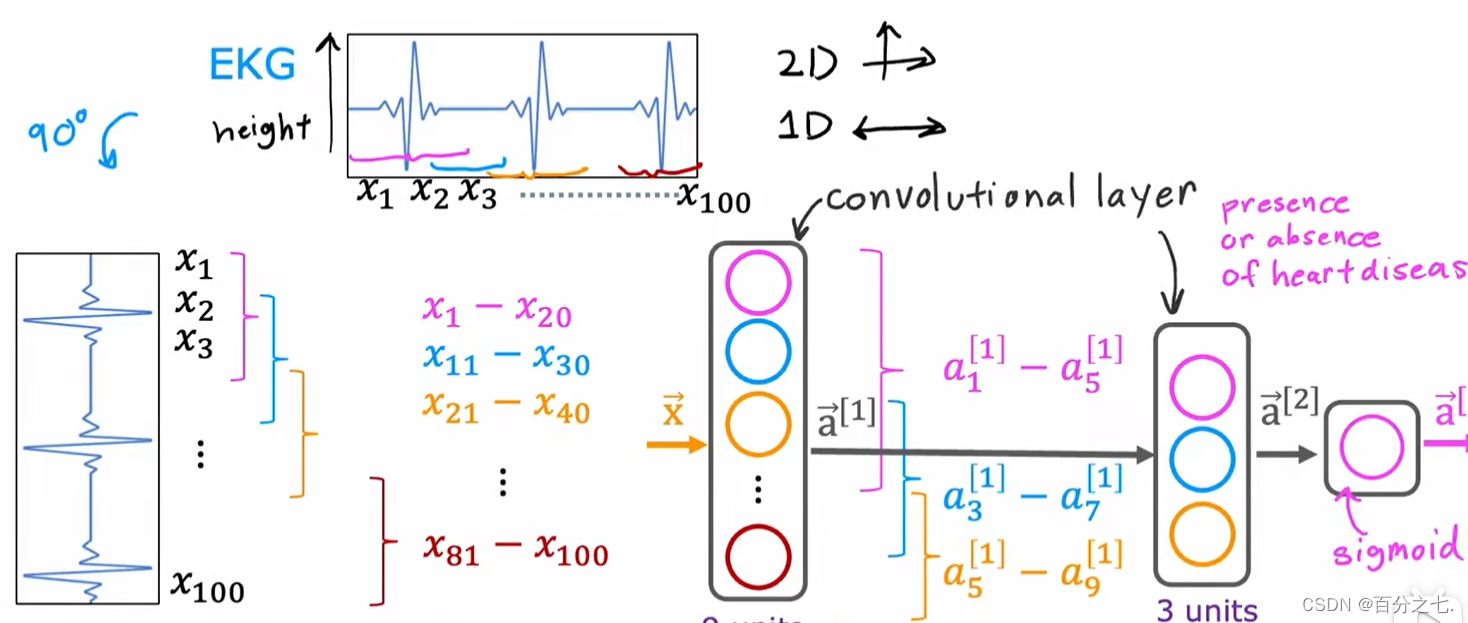
神经网络中的网络层
神经网络的预测：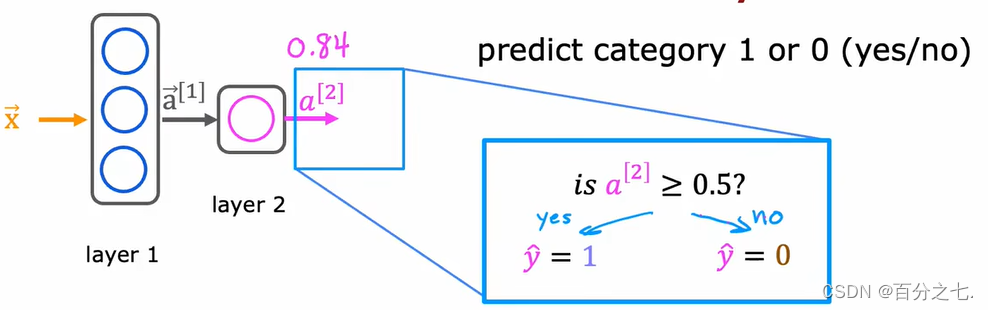
每一层都输入一个数字向量，并对其应用逻辑回归单元，然后计算出另一个数字向量，从一层到下一层，直到得到最终的输出层的计算结果。并可以将阈值设为0.5，得出最终的预测。
更复杂的神经网络：
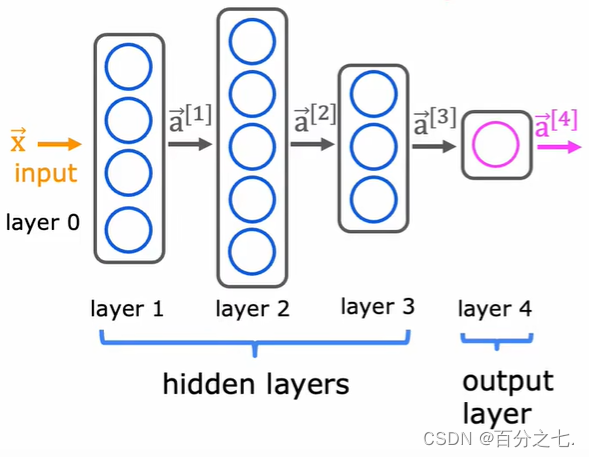
这个网络有4层，第0层是输入层，1、2、3是隐藏层，4层是输出层。
a
j
[
l
]
=
g
(
w
?
j
[
l
]
?
a
?
[
l
?
1
]
+
b
j
l
[
l
]
)
a_{j}^{[l]}=g\left(\vec{w}_{j}^{[l]} \cdot \vec{a}^{[l-1]}+b_{j l}^{[l]}\right)
aj[l]?=g(wj[l]??a[l?1]+bjl[l]?)
g是激活函数(activation function)，因为g输出这个激活值。激活函数就是输出激活值的函数。
sigmoid激活函数的替代方案
1.ReLU激活函数：
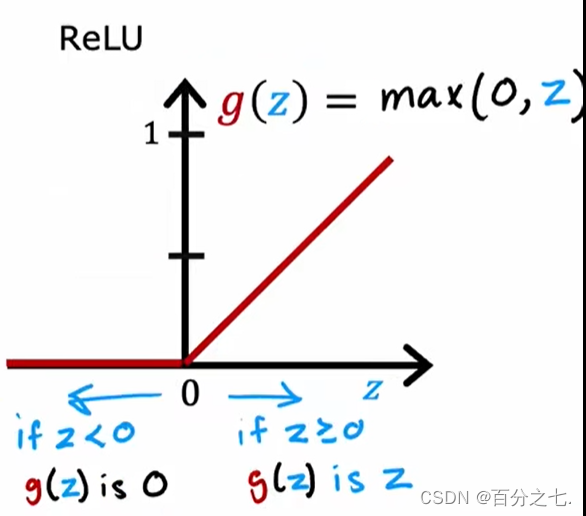
2.线性激活函数：
g(z)=z
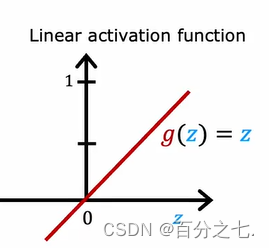
如何选择激活函数
我们可以在神经网络中的不同神经元中选择不同的激活函数，但在考虑激活函数对于输出层的预测标签时，总是会有一个相当自然的选择。如果正在处理的是一个二分类问题，那么在输出层中使用sigmiod激活函数；如果正在处理回归问题，那么将会用到不同的激活函数，如线性激活函数。最后如果输出值只能取非负值，那么最自然的选择将是ReLU激活函数。
事实证明，ReLU激活函数是迄今为止神经网络中最常见的选择。其中一个原因是它的计算速度要快一些，效率高。更重要的一个原因是ReUL激活函数的图像仅在图形的左半部分中变平，而sigmoid激活函数在图形的左右两侧都变平，如果使用梯度下降来训练神经网络将会变得很慢。所以ReUL激活函数是隐藏层中最常见的激活函数。
为什么模型需要激活函数？
如果我们在神经网络中的所有节点使用线性激活函数，那么这个大型神经网络将会变得与线性回归没有什么不同。
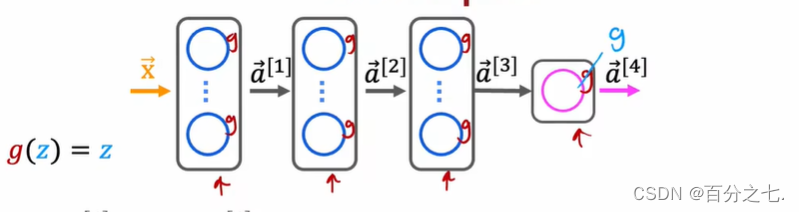
在这种情况下，这个模型等同于逻辑回归，所以这个大型神经网络没有做任何不能用逻辑回归做的事情，这就是为什么一个常见的经验法则是不要在神经网络的隐藏层中使用线性激活函数。
多分类问题：
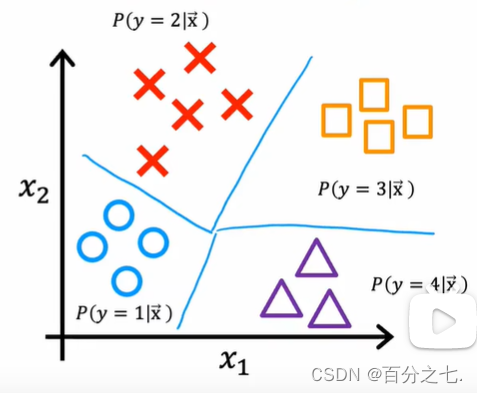
Softmax回归算法
softmax回归算法是逻辑回归的推广。
逻辑回归的损失函数：
loss
?
=
?
y
log
?
a
1
?
(
1
?
y
)
log
?
(
1
?
a
1
)
\operatorname{loss}=-y \log a_{1}-(1-y) \log \left(1-a_{1}\right)
loss=?yloga1??(1?y)log(1?a1?)成本函数：
J
(
w
→
,
b
)
=
?average?loss?
J(\overrightarrow{\mathrm{w}}, b)=\text { average loss }
J(w,b)=?average?loss?softmax回归方程：
a
1
=
e
z
1
e
z
1
+
e
z
2
+
?
+
e
z
N
=
P
(
y
=
1
∣
x
→
)
?
a
N
=
e
z
N
e
z
1
+
e
z
2
+
?
+
e
z
N
=
P
(
y
=
N
∣
x
→
)
\begin{gathered} a_{1}=\frac{e^{z_{1}}}{e^{z_{1}}+e^{z_{2}}+\cdots+e^{z_{N}}}=P(y=1 \mid \overrightarrow{\mathrm{x}}) \\ \vdots \\ a_{N}=\frac{e^{z_{N}}}{e^{z_{1}}+e^{z_{2}}+\cdots+e^{z_{N}}}=P(y=N \mid \overrightarrow{\mathrm{x}}) \end{gathered}
a1?=ez1?+ez2?+?+ezN?ez1??=P(y=1∣x)?aN?=ez1?+ez2?+?+ezN?ezN??=P(y=N∣x)?损失函数：
loss
?
(
a
1
,
…
,
a
N
,
y
)
=
{
?
log
?
a
1
?if?
y
=
1
?
log
?
a
2
?if?
y
=
2
?
?
log
?
a
N
?if?
y
=
N
\operatorname{loss}\left(a_{1}, \ldots, a_{N}, y\right)=\left\{\begin{array}{cc} -\log a_{1} & \text { if } y=1 \\ -\log a_{2} & \text { if } y=2 \\ & \vdots \\ -\log a_{N} & \text { if } y=N \end{array}\right.
loss(a1?,…,aN?,y)=?
?
???loga1??loga2??logaN???if?y=1?if?y=2??if?y=N?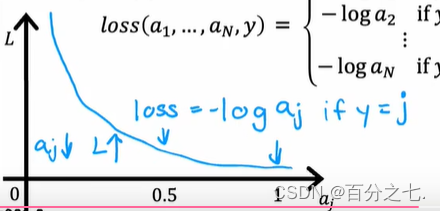 
多标签分类问题
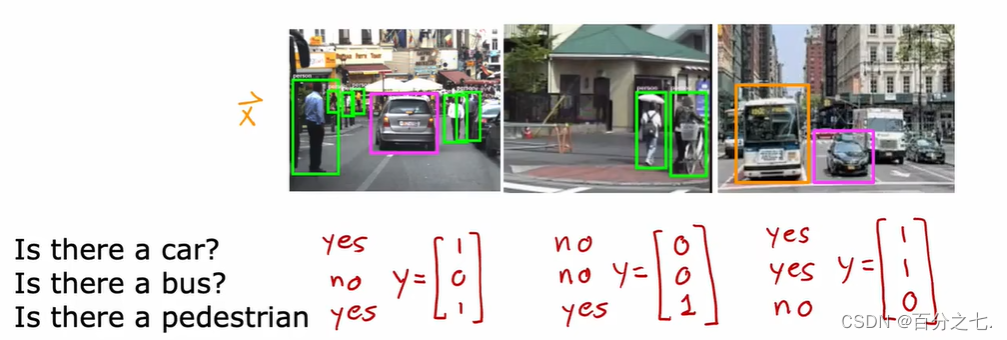
如何为多标签分类建立一个神经网络？
一种解决方法是将其视为三个完全独立的机器学习问题，可以建立一个神经网络判断有没有汽车，第二个检测公交车，第三个检测行人。
还有一种方法可以同时做到这一点，即训练单个神经网络同时检测所有汽车、公交和行人。
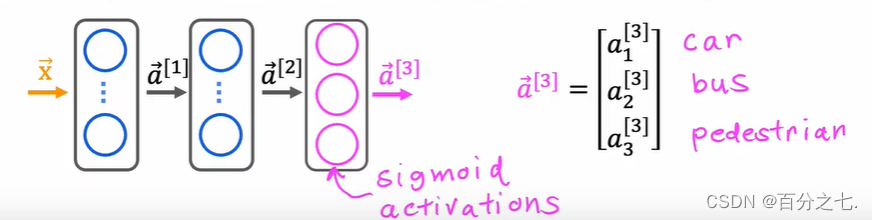
只需解决三个二分类问题，在输出层中的三个节点使用sigmoid激活函数。
高级优化方法
Adam优化算法可以自适应学习率，比梯度下降算法快得多。
梯度下降的表达式：
w
j
=
w
j
?
α
?
?
w
j
J
(
W
?
,
b
)
w_{j}=w_{j}-\alpha \frac{\partial}{\partial w_{j}} J(\vec{W}, b)
wj?=wj??α?wj???J(W,b) 成本函数的图像：如果α太小：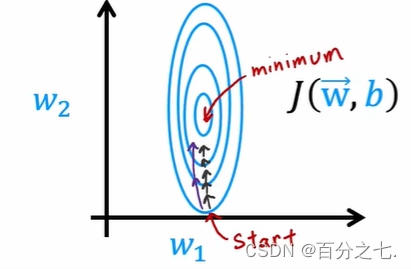
Adam算法可以自动增加α，让它采取更大的步骤并更快地达到最小成本。
如果α太大：
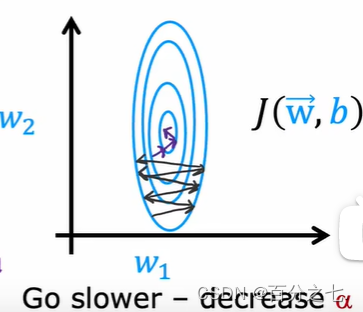
此时Adam算法可以自动减小α。
其他网络层类型
前面我们一直使用的是神经元激活的密集层，比如第二个隐藏层是来自前一层的每个激活值的函数。
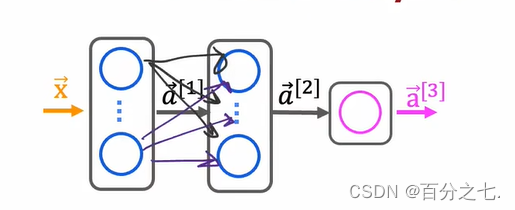
但设计神经网络的人可能会选择使用不同类型的层，比如卷积层。如果在神经网络中有多个卷积层，则被称为卷积神经网络。
为什么使用卷积层？
1.加快计算速度
2.需要更少的训练数据，不容易过度拟合。
隐藏层中的单元只查看输入的有限窗口：
