文章目录
清风课程笔记 正课第十讲
聚类模型

K-means聚类算法

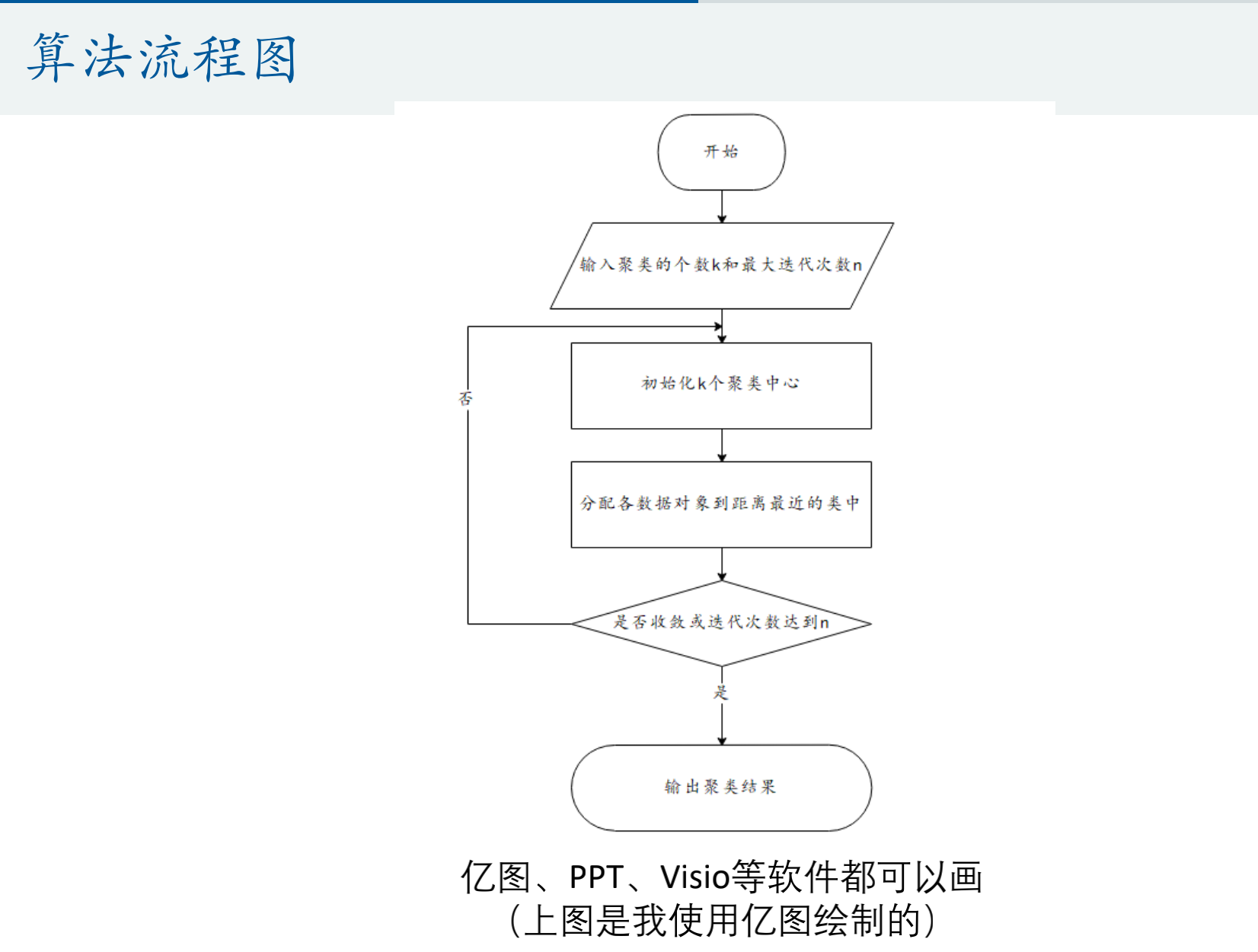

k-means++算法
- k-means++主要是使初始的聚类中心距离尽可能远,这种方法解决了对初值敏感的问题
- 这样就很可能让一个孤立点自成一类
- 解决了受异常点影响的问题

SPSS操作

- 结果
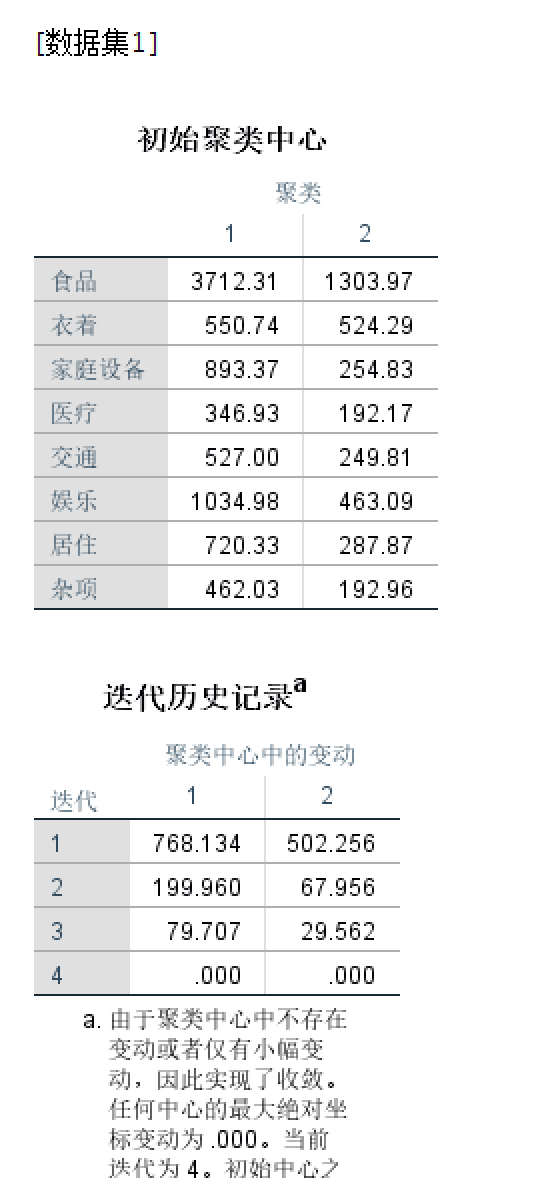
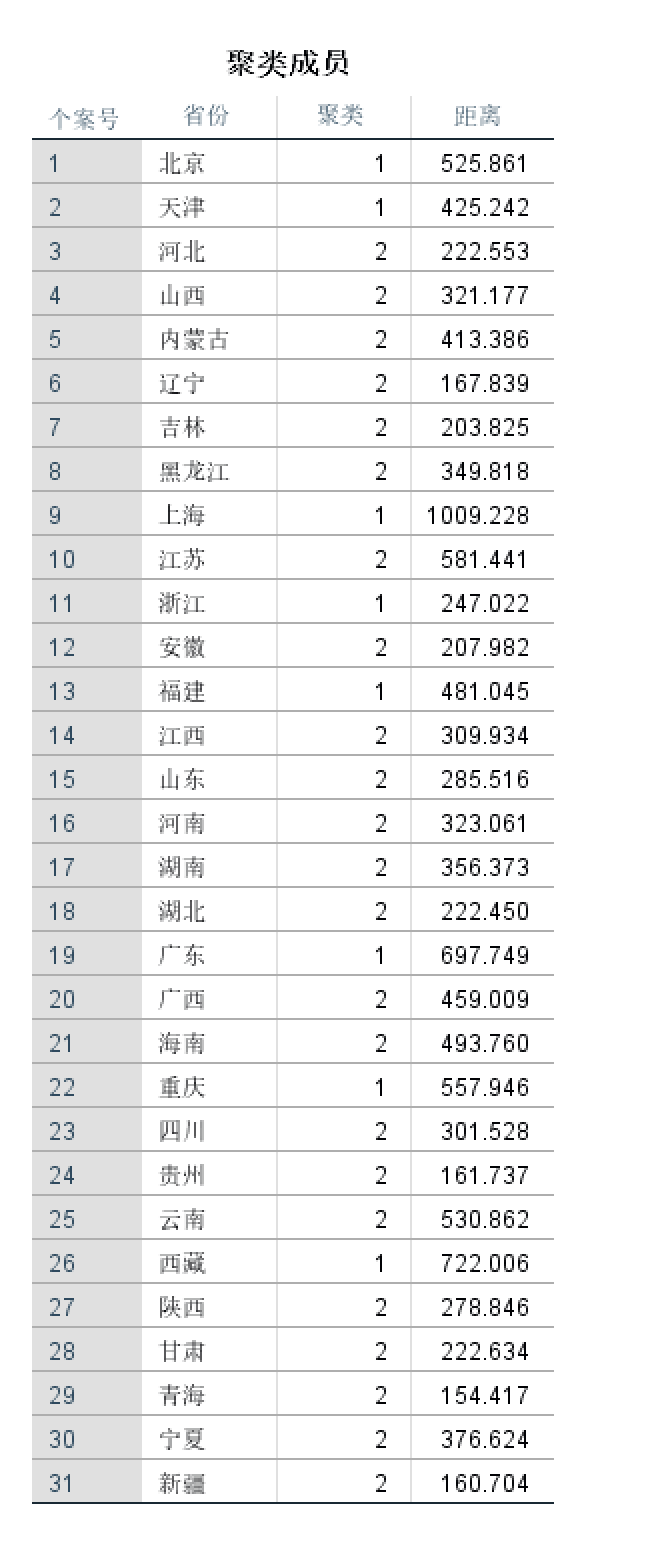
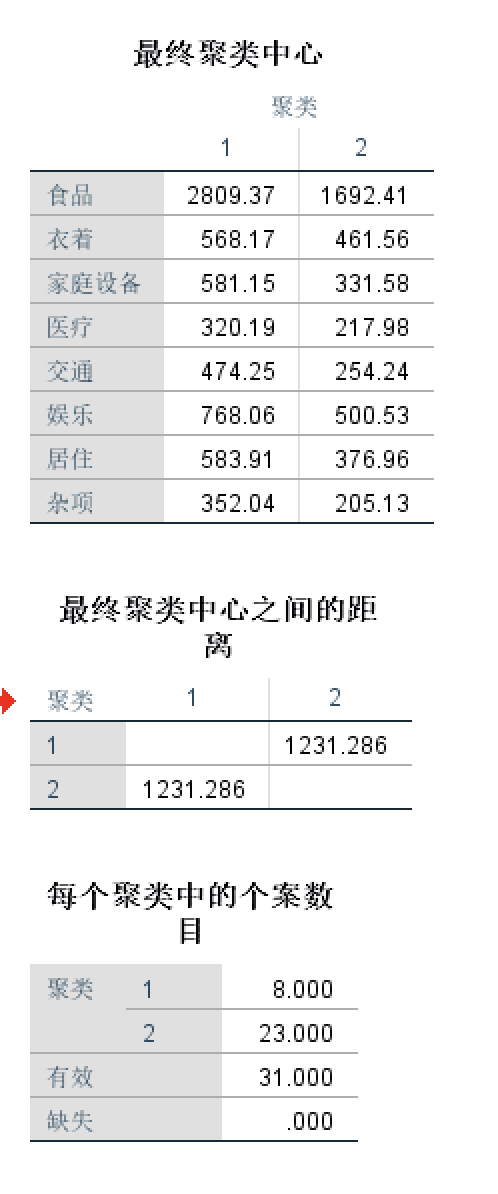
一些讨论

- k取值看怎样效果好,好解释
- 如果题目中数据量纲(单位)不同时,要先标准化
- 标准化结果
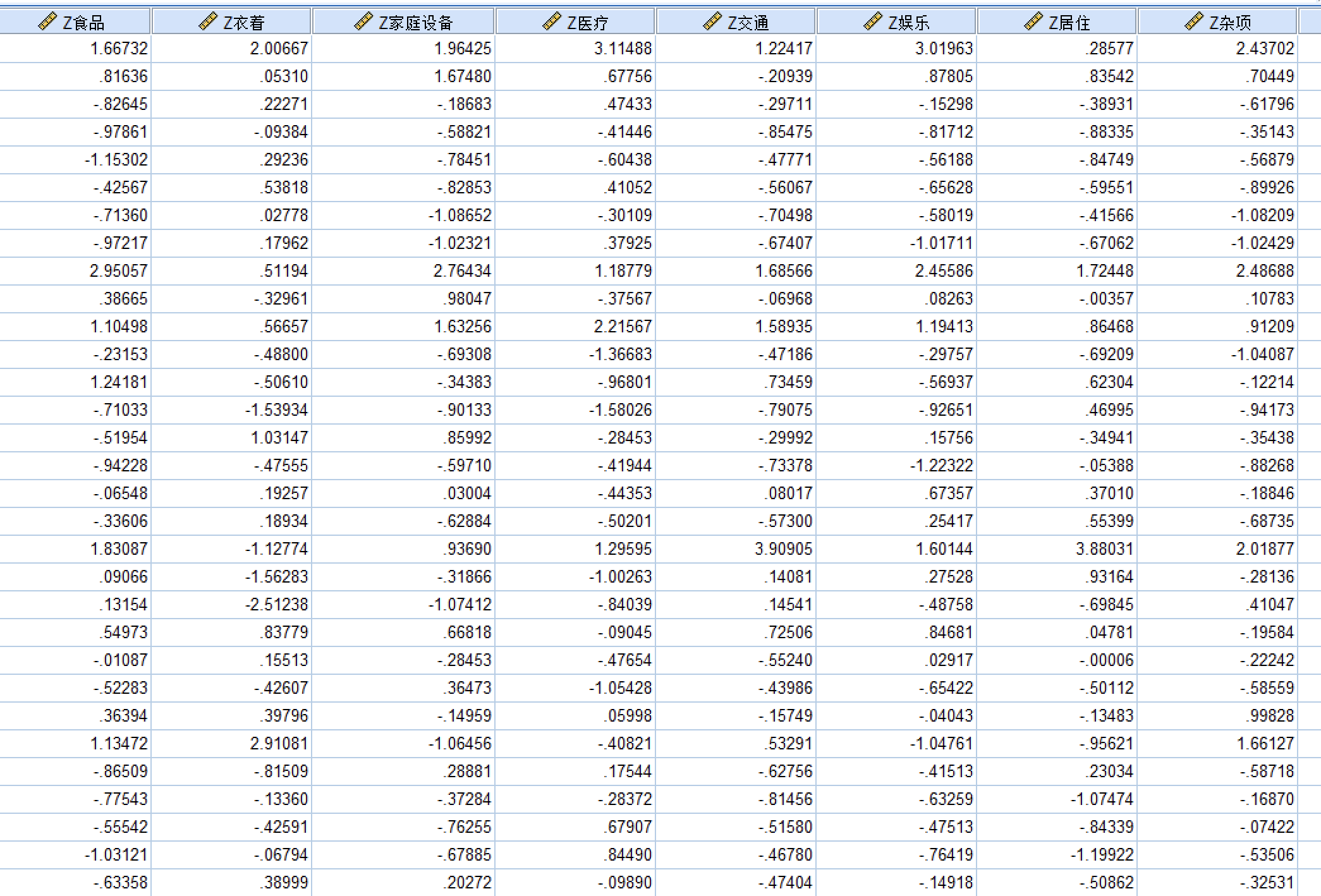
- 再用这些数据去标准化
- 标准化还原聚类中心
- 只要乘标准差再+均值就行
tips:数据多的时候论文中可以先加一个描述统计
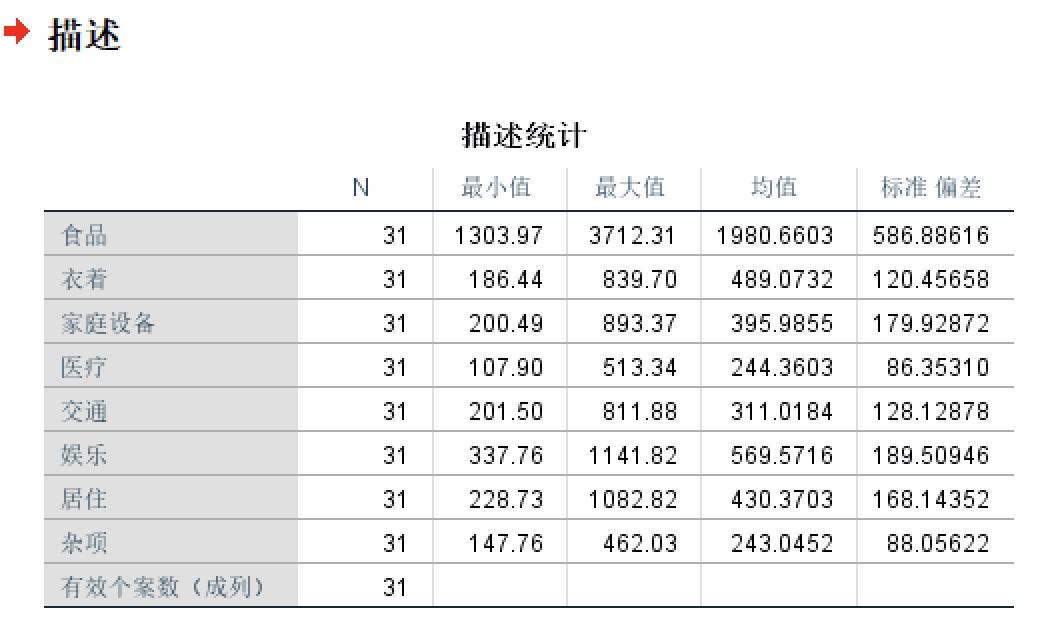
系统聚类
不用我们在开始时确定k值
举例
题目
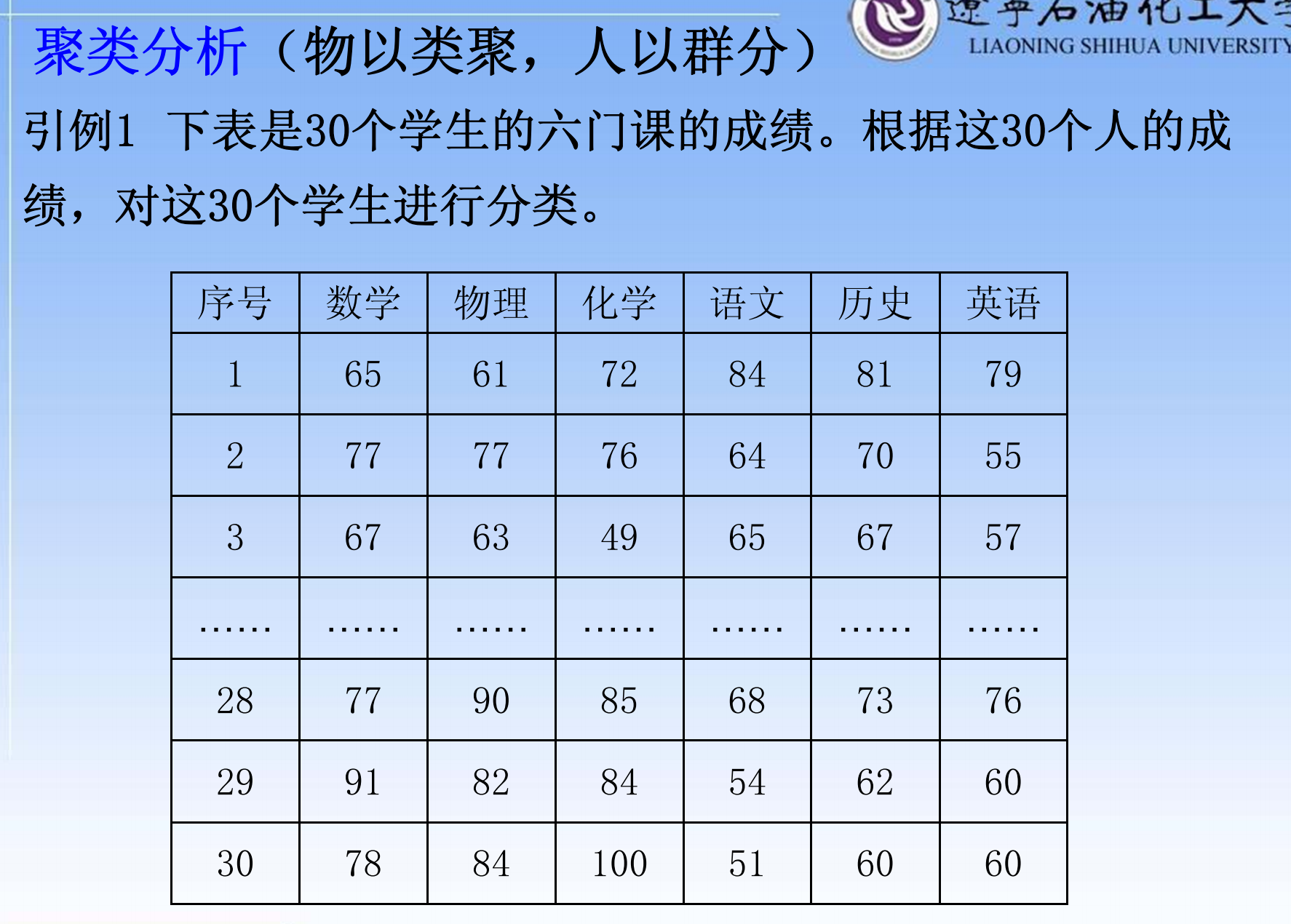
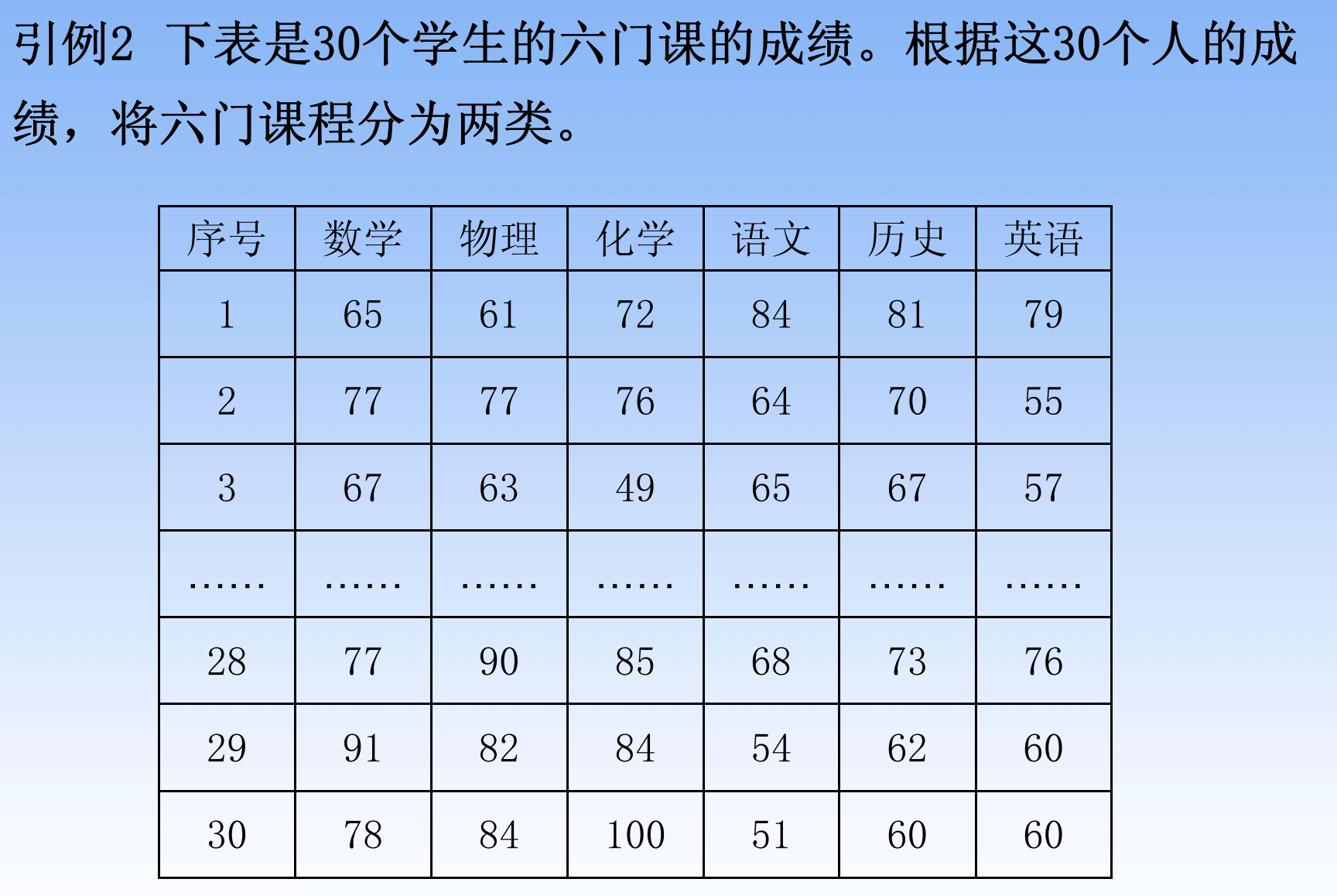
- 两个例子,一个是对样本进行分类,一个是对指标进行分类(比较罕见)
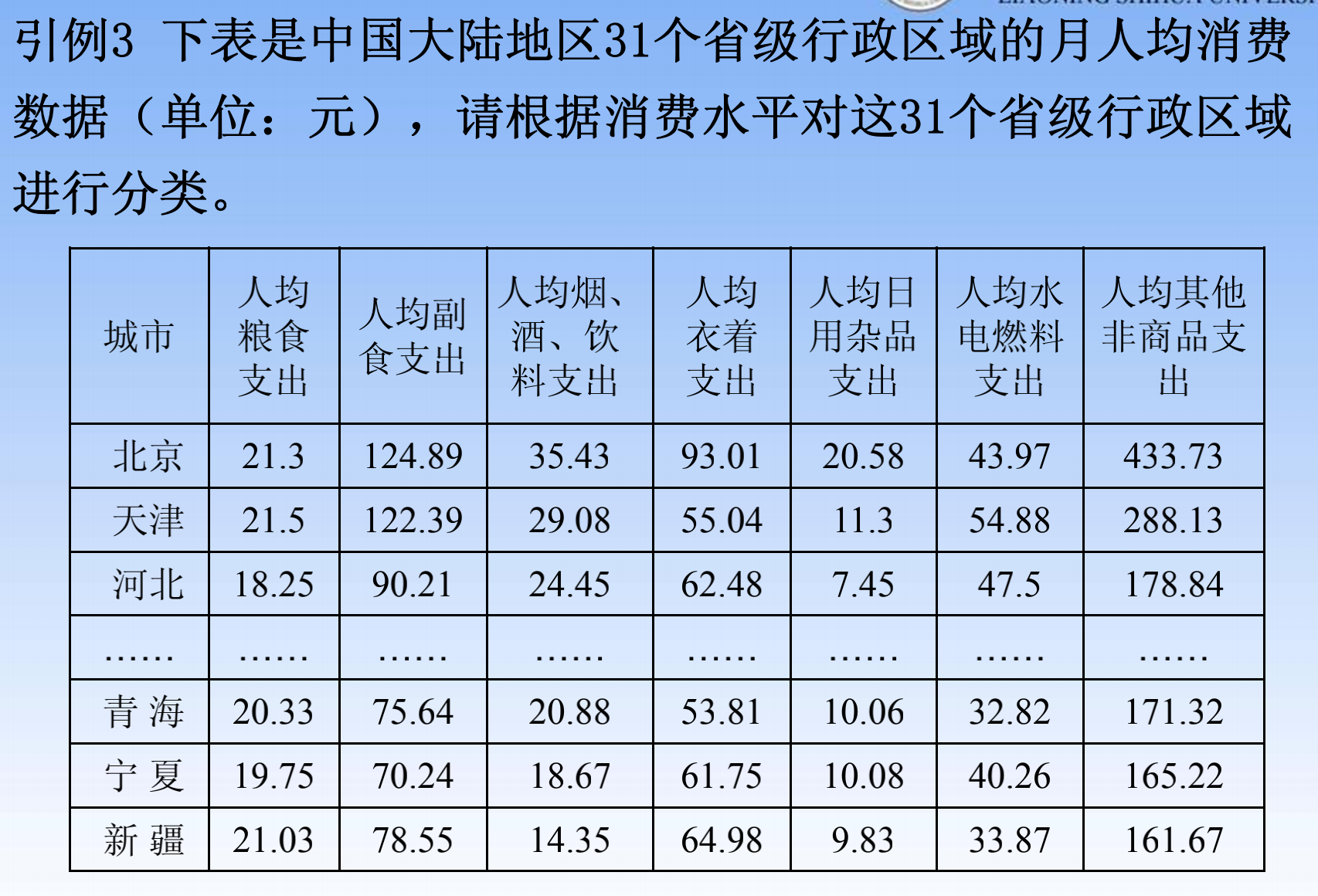
如何分类
- 只考虑一个指标
- 找最相近的两个点,归为一类,计算重心(重心跟其他的点一样,相互计算距离)
- 然后再找最相近的两个点,归为一类
- 不断迭代

- 只考虑两个指标
- 原理同上
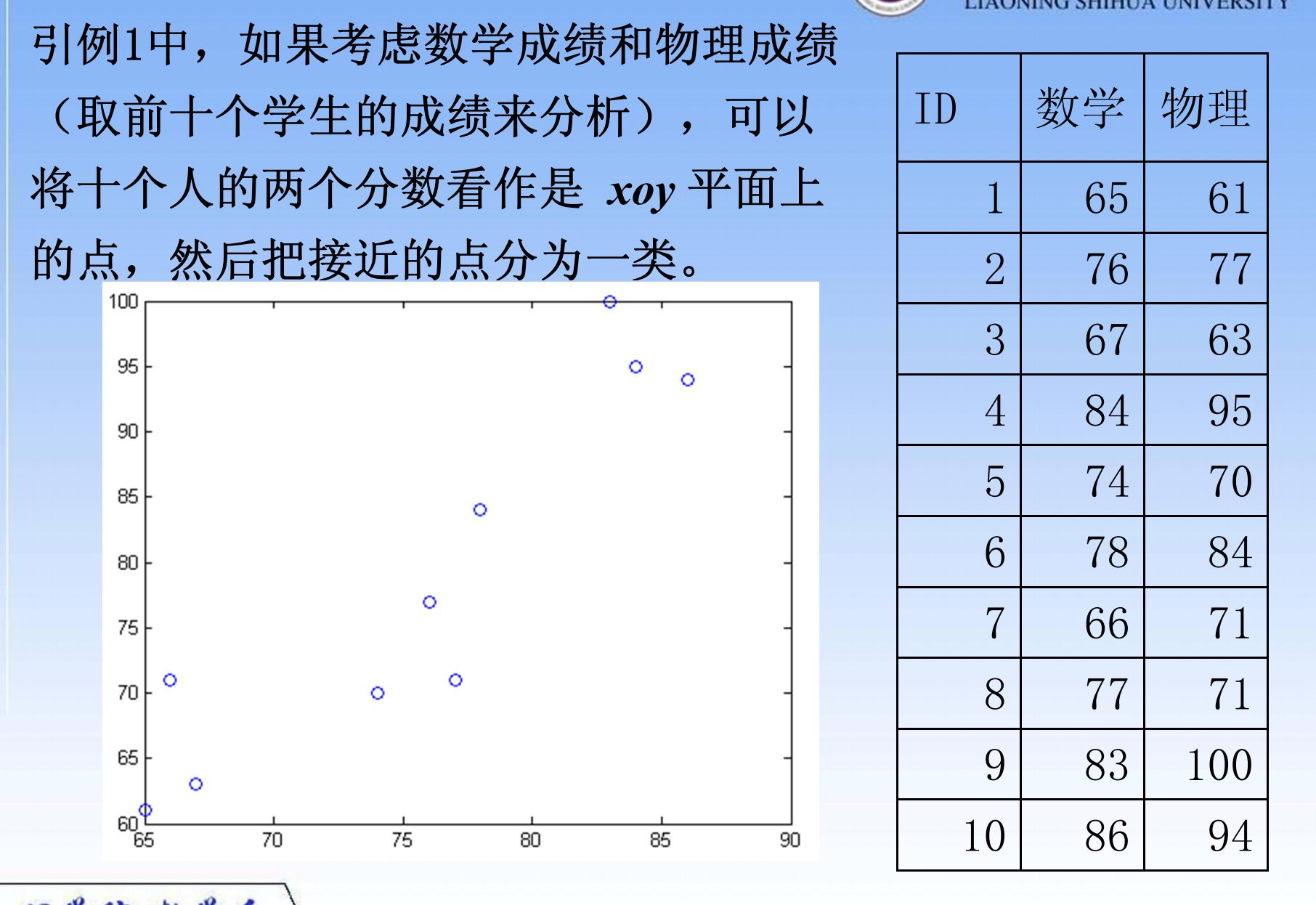
- 分类准则
常用距离

- 绝对值距离:网状道路常用
- 欧式距离:常用
- 下面三种用的较少

- 这里只计算了一次,实际上每两个样本之间都要算一次距离
指标与指标之间的距离

- 如例2一样对指标分类的题目较少
- 所以用到了再学
类与类之间的距离
与常用距离不同的是,这里有了类的概念,而不只是一个个的样本点

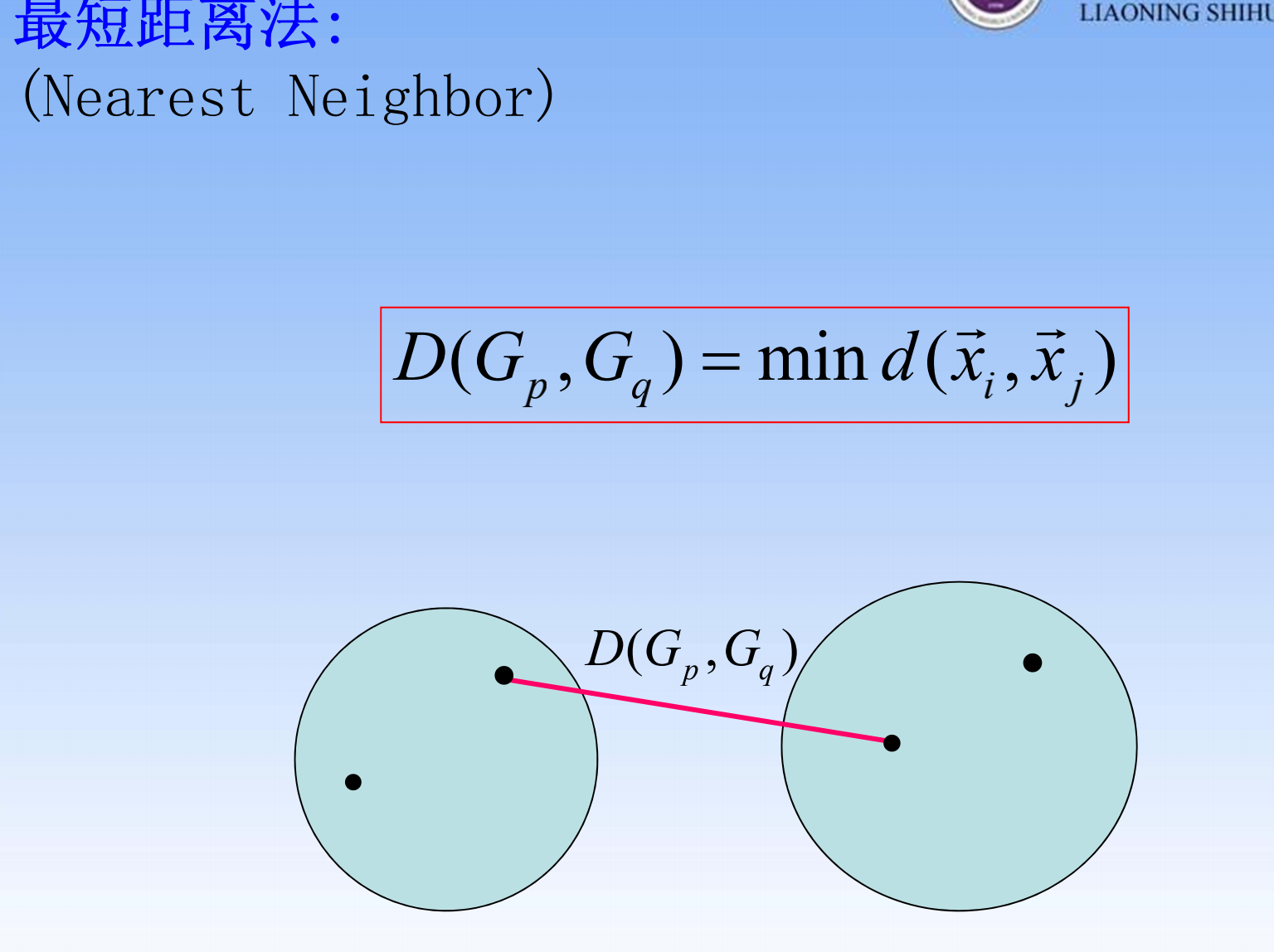
- 最短距离法
- 最长距离法
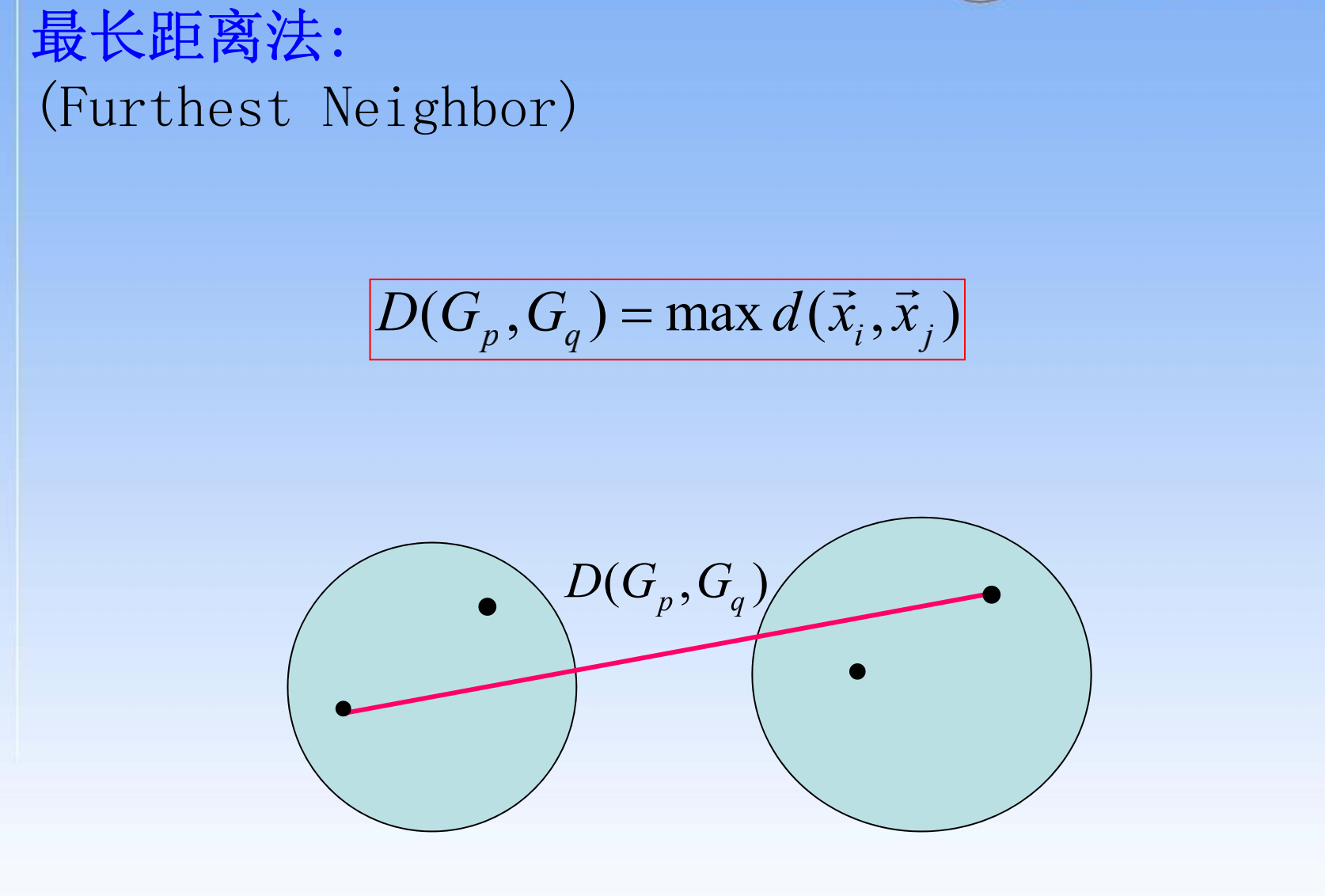
- 组间平均连接法
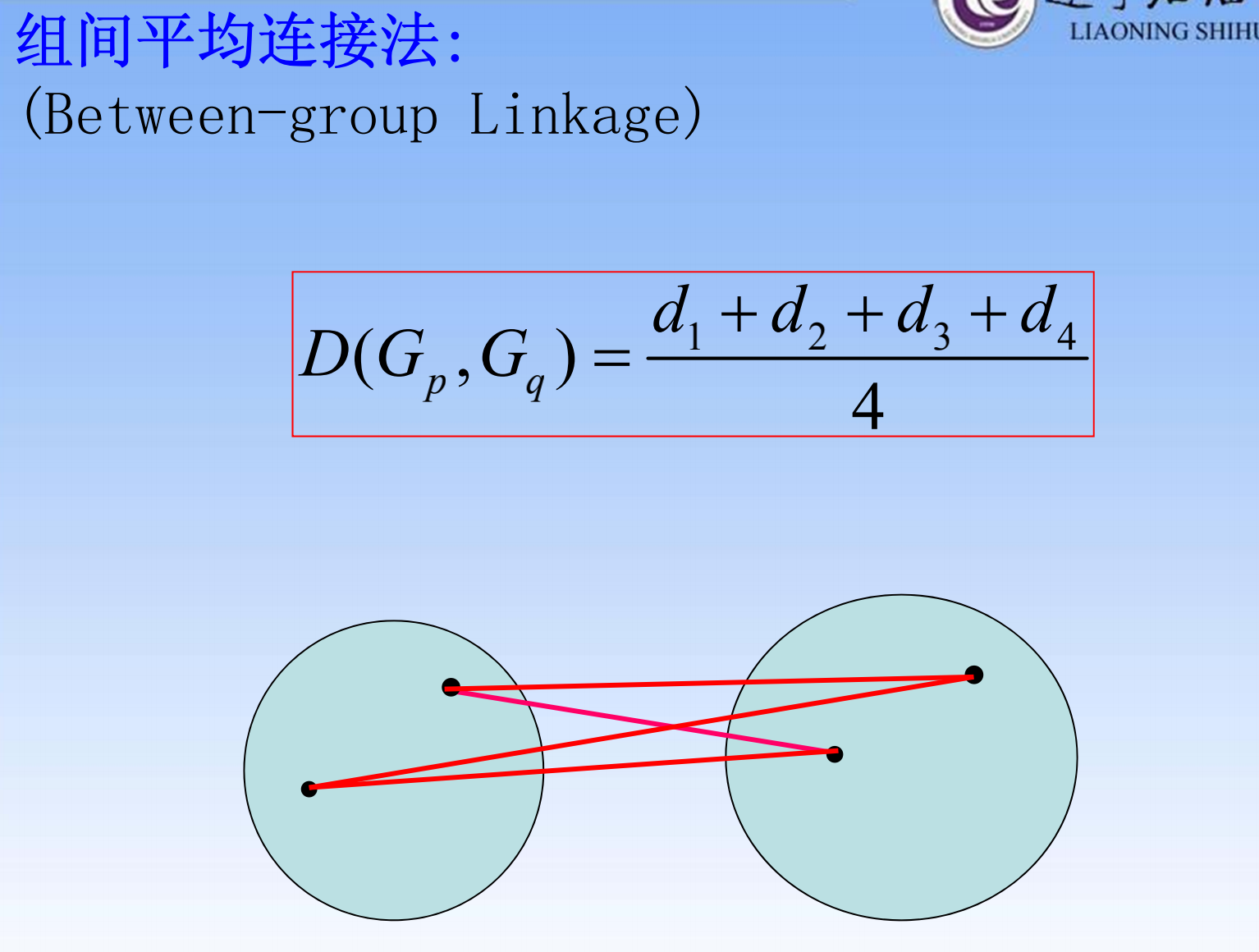
- 组内平均连接法
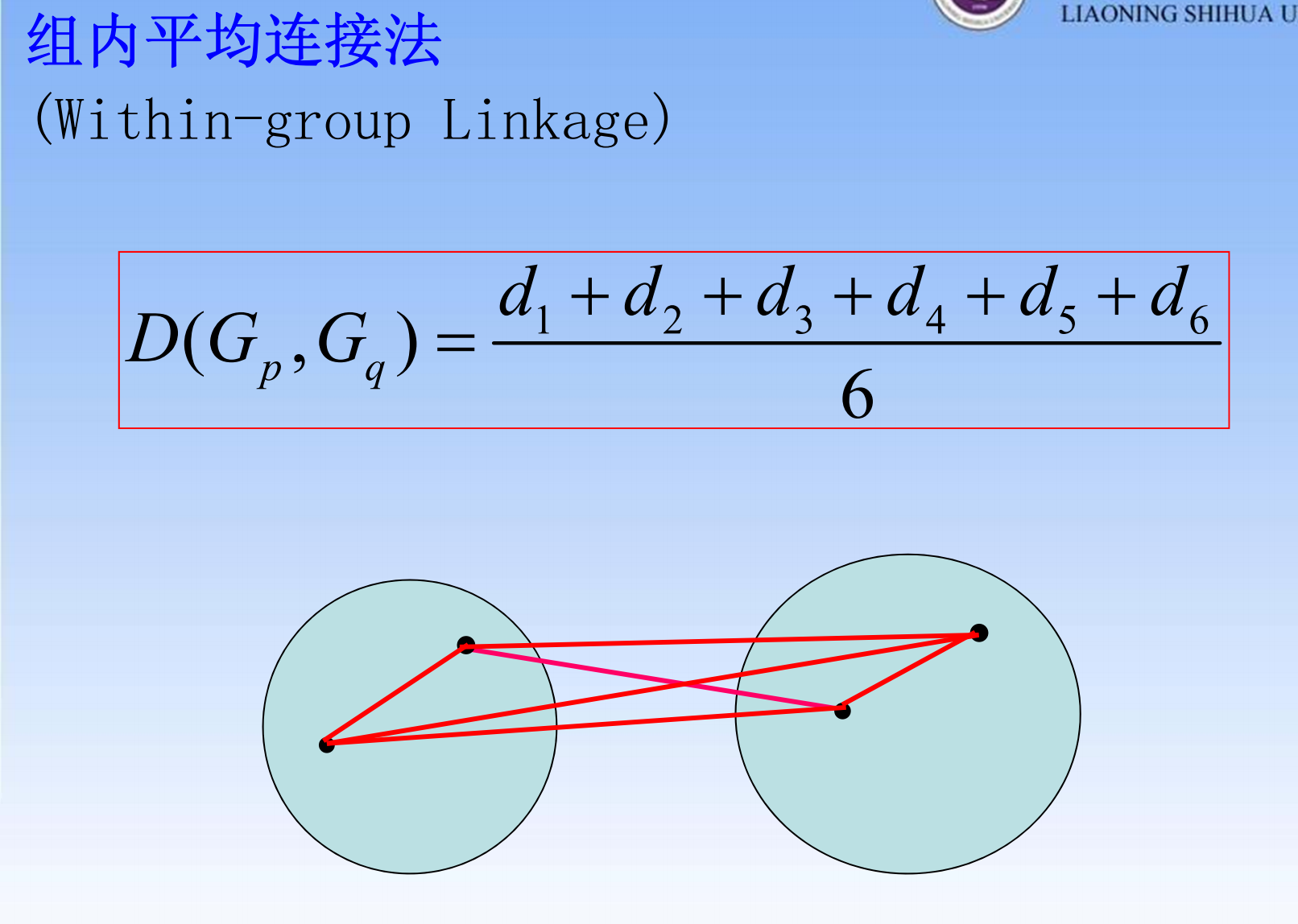
- 重心法
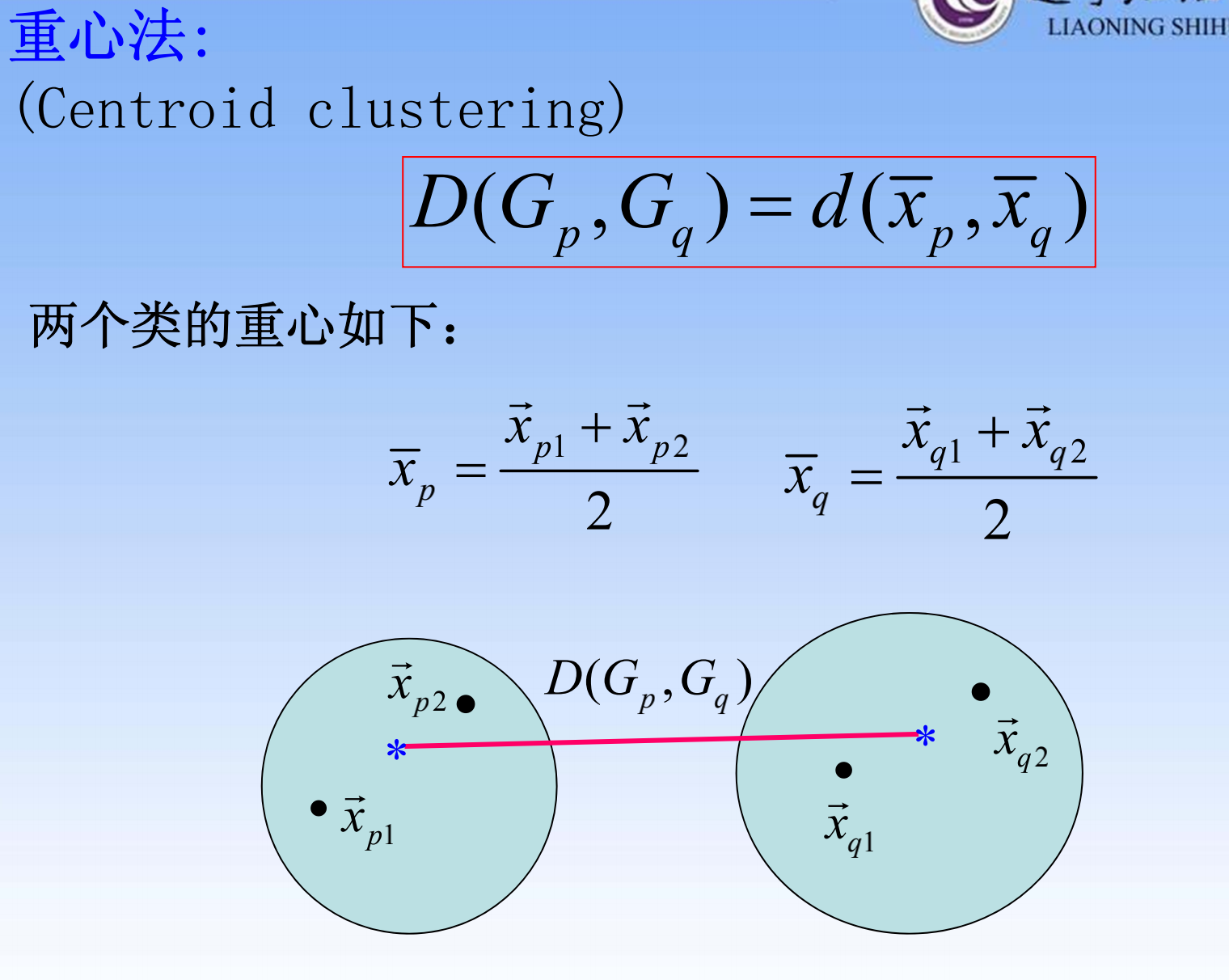
常用组间、组内,也会用重心法,实际上只要解释的通就行
过程
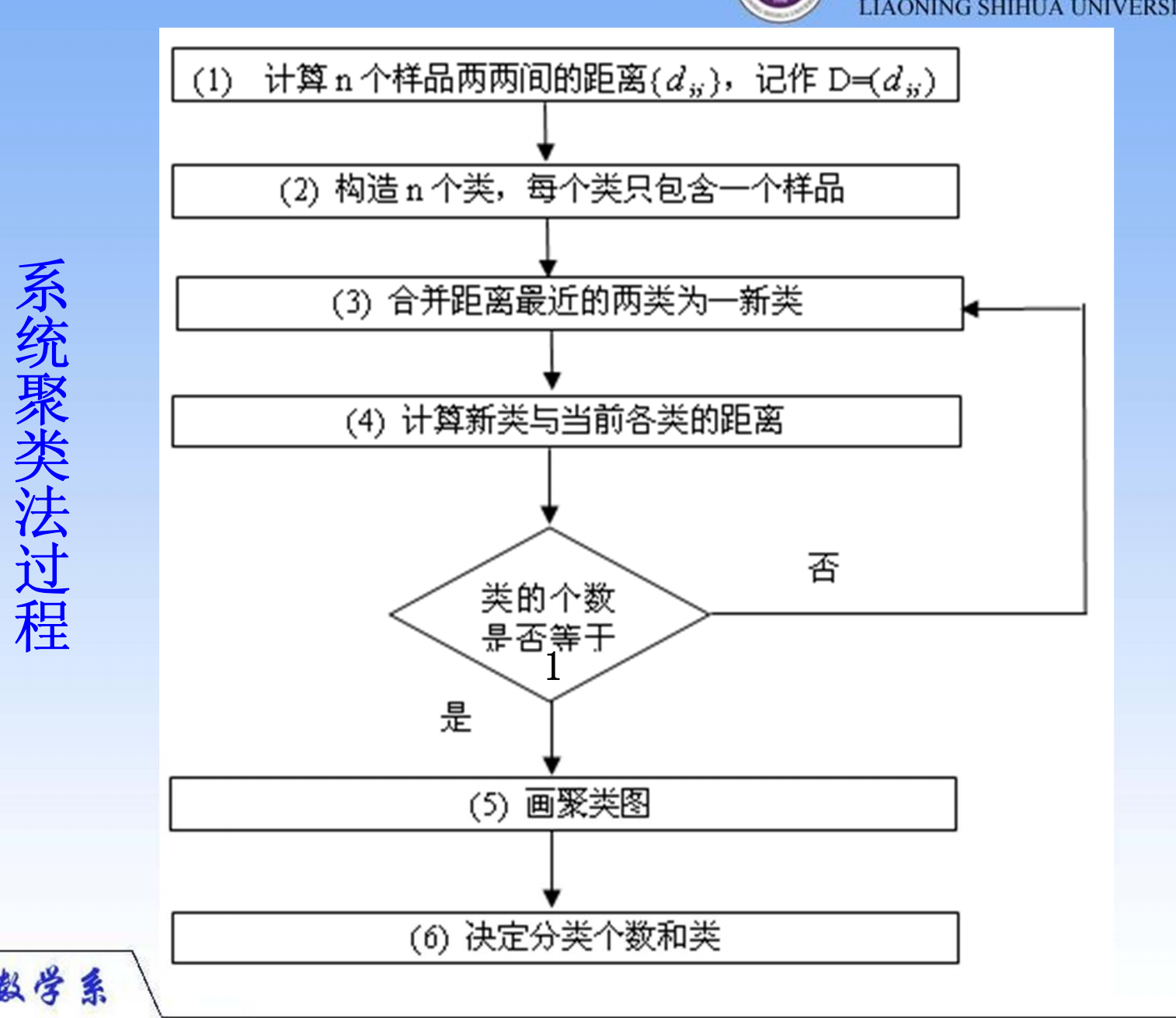
- 论文中要自己做一张跟这个不同的图
最短距离系统聚类
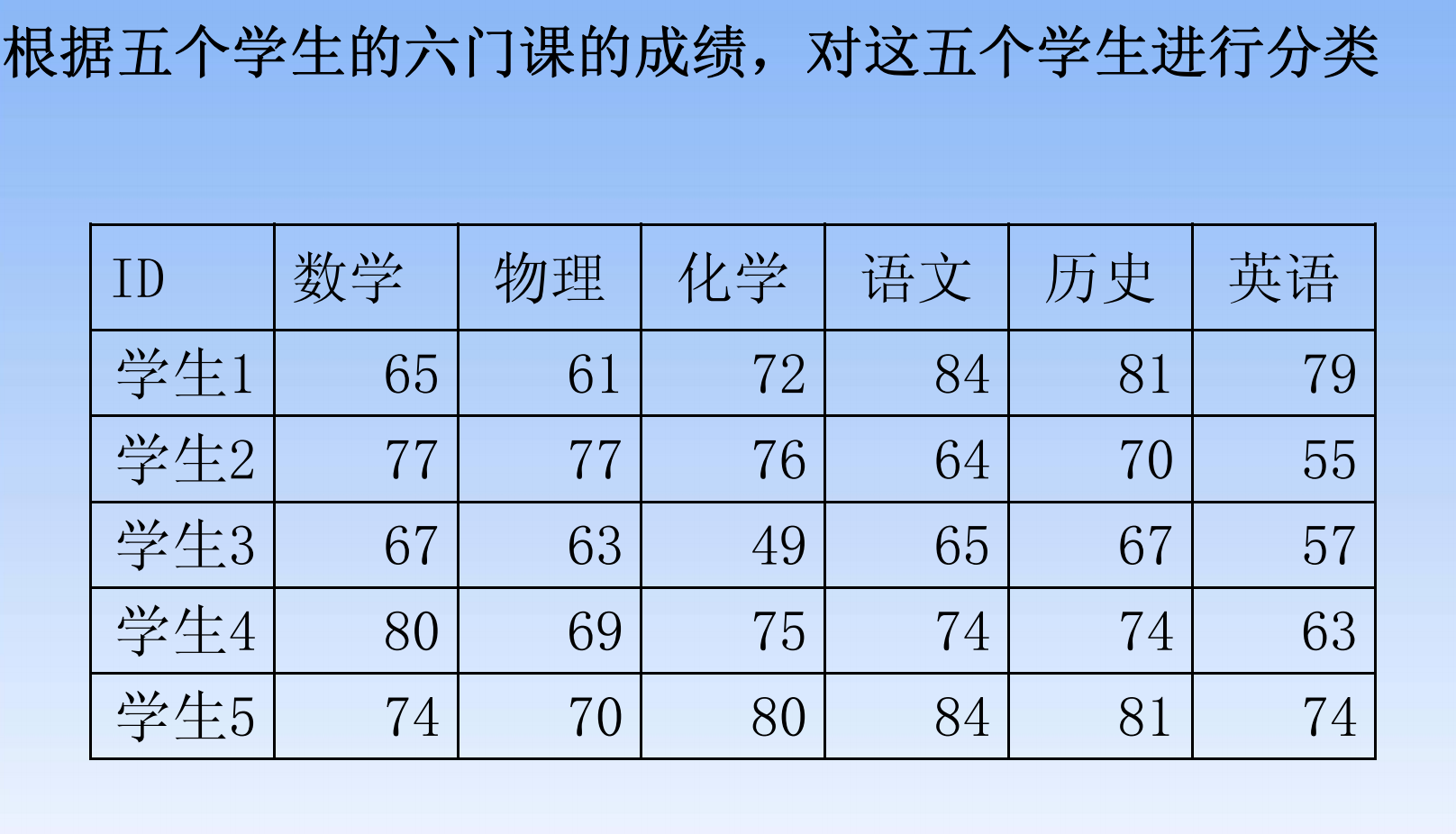
- D是对称矩阵,各样本间距离
- 每个样本看作一个类,距离最小的两个类聚为一类
- 计算该类和剩余几类的距离(这里算得是最短距离),得到新的距离矩阵

- 之后就是重复上述步骤
- 循环两次


直到最后只有一类,最后聚类
- 聚类谱系图
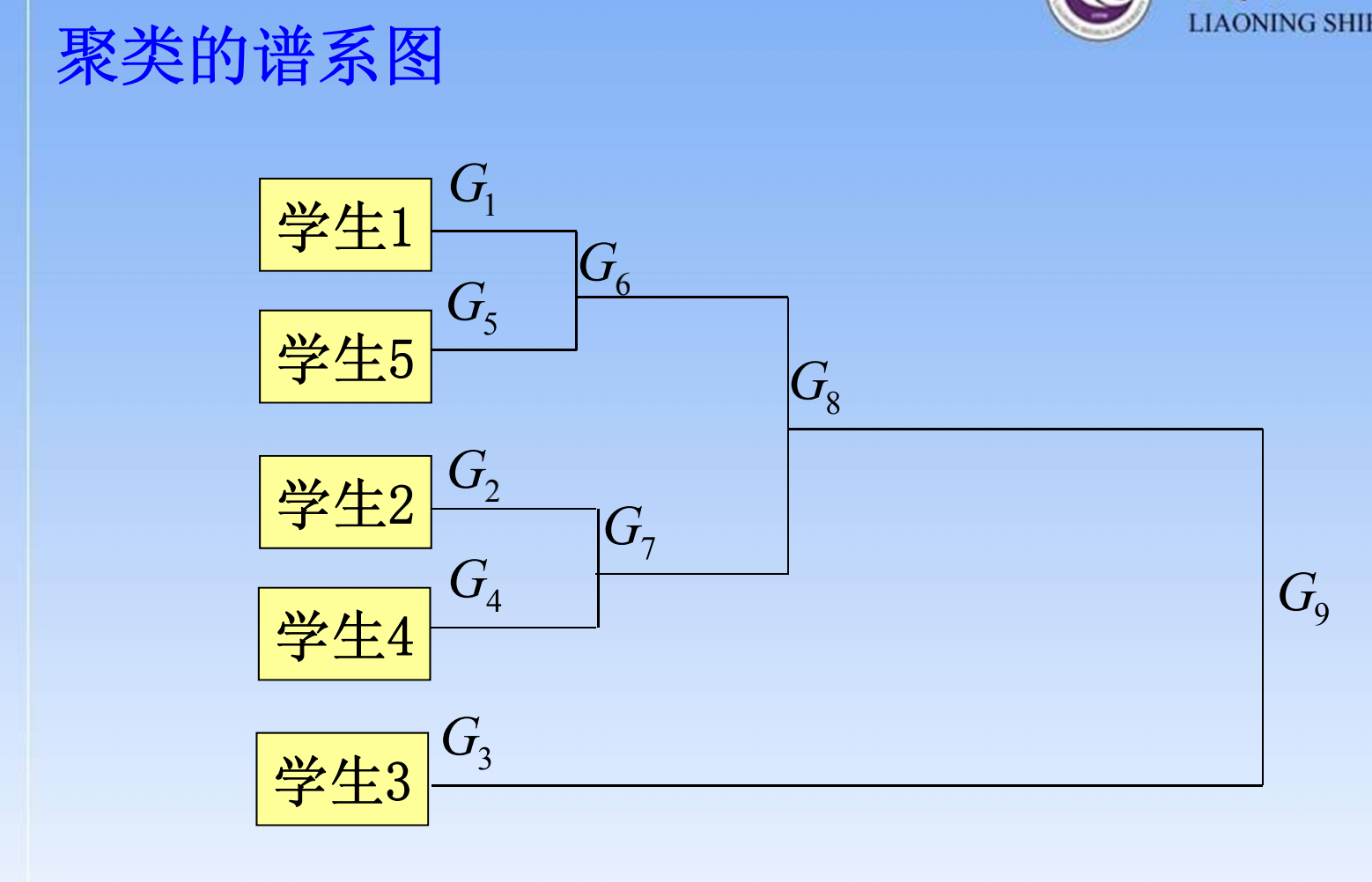
- 最后想聚多少类,只要根据图倒推就行
说明

- 这是最长距离聚类的结果,可以看到跟最短距离聚类是不同的
- 实际上,只要聚类的结果能够解释的通,我们就可以选择那个方法来进行聚类

- 逻辑上聚类不太明白,需要我们自己对结果做一个合理的解释,说明每个类的含义是啥
- 说明

SPSS操作
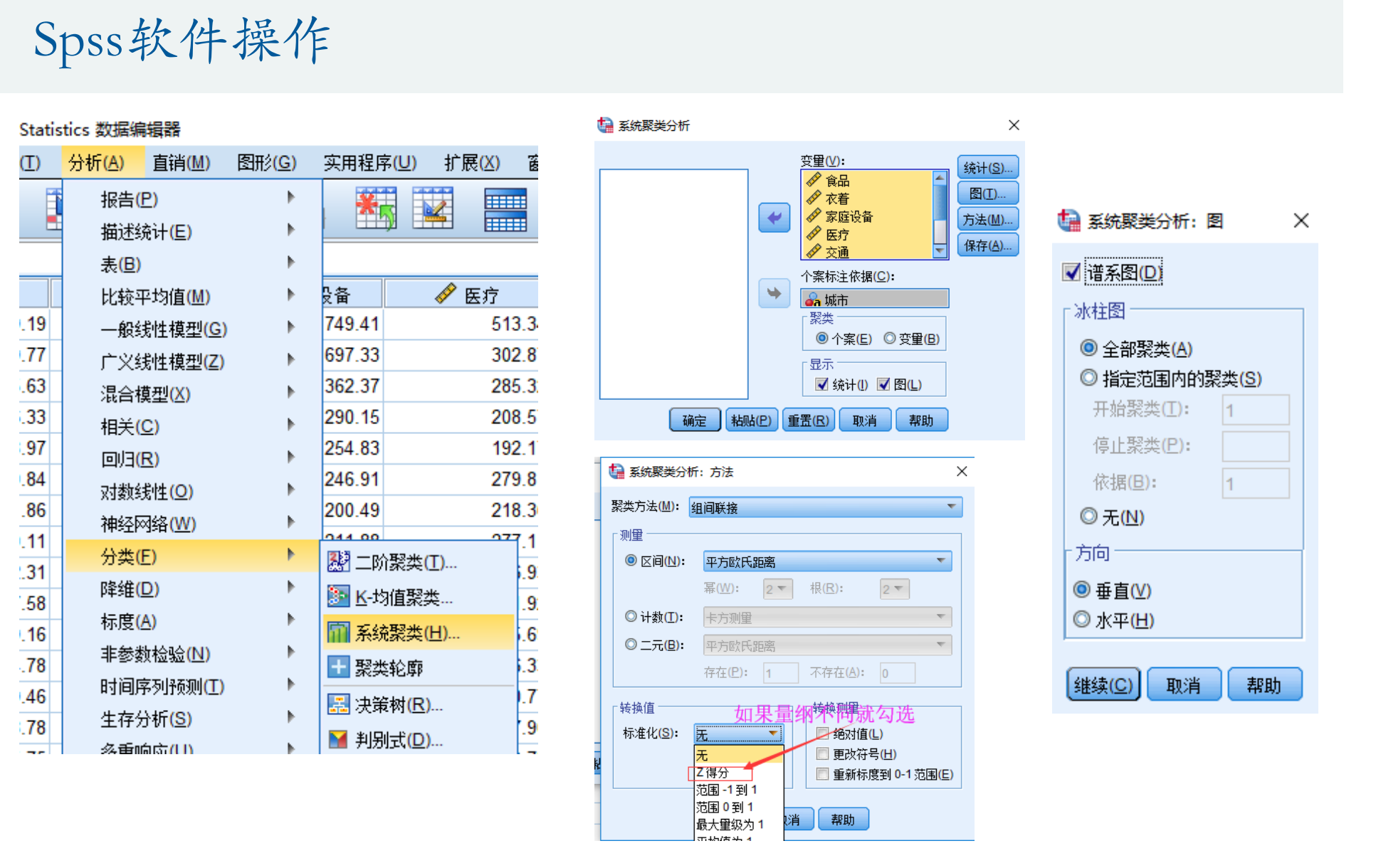
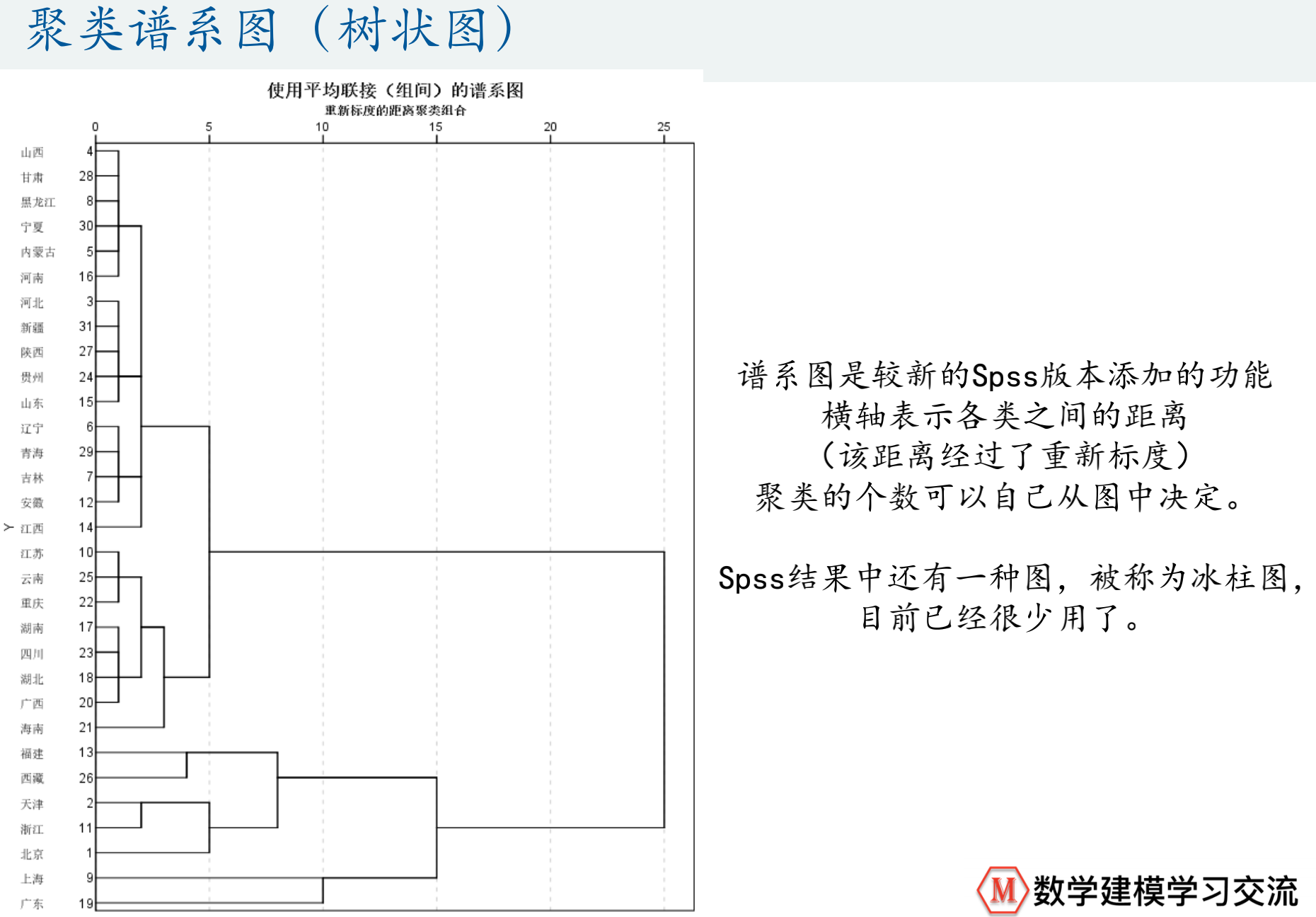
- SPSS的谱系图先将一些靠在一起
确定聚类数量
肘部法则

-
这里的绝对值只是距离的记号,不是求绝对值
-
各个类的畸变程度
-
各个类畸变程度相加->所有类总的畸变程度(我们要的就是这个)
-
k越大,聚合程度减小(最极端就是一个样本就是一个类,那么很多类的畸变程度都是0)
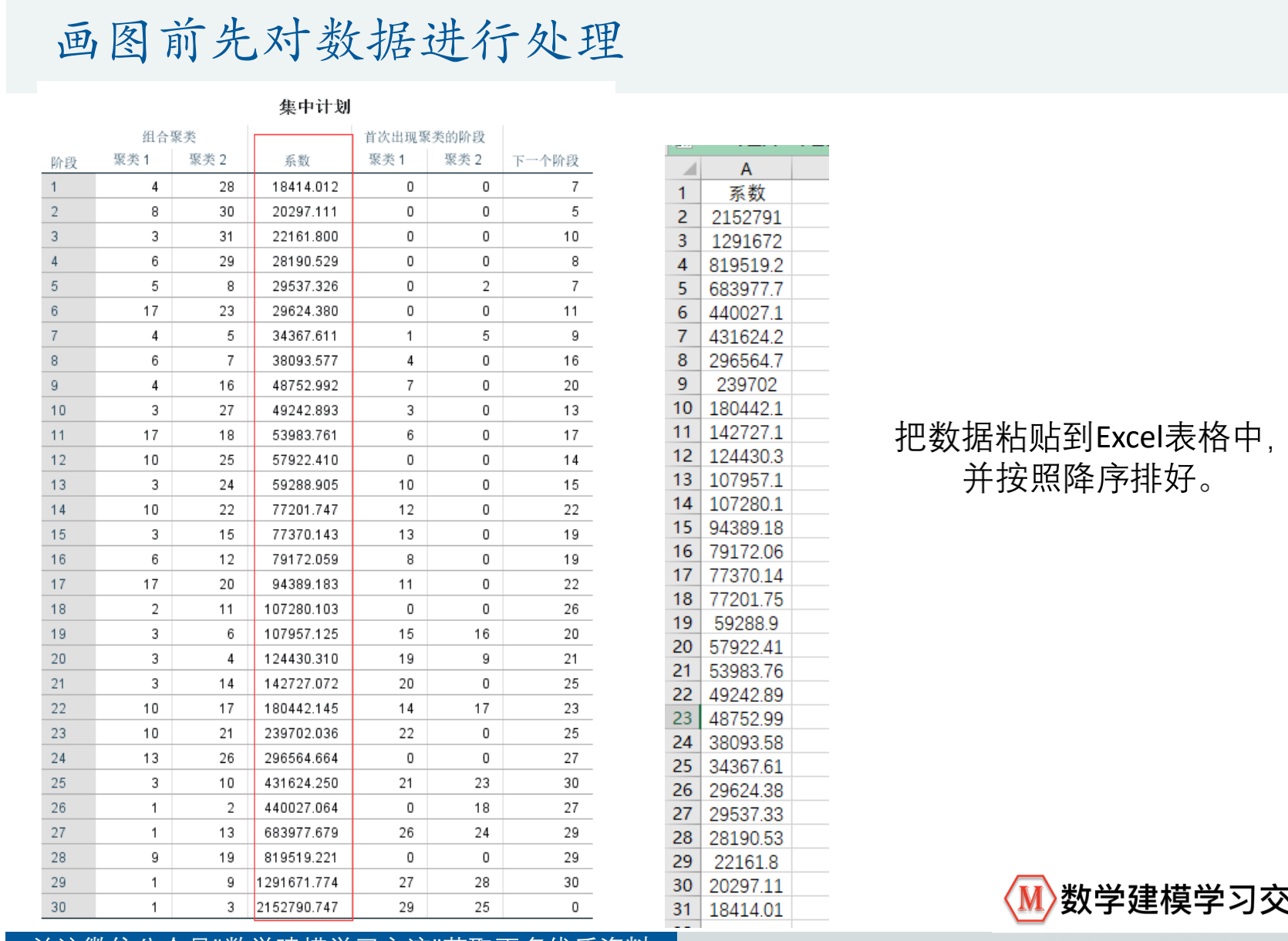

- SPSS软件中表的系数就是聚合系数,复制到excel,降序
- 一般要选择匹配目标格式
- 插入散点图(肘部图)
- 美化图
- 分析解释,两种解释中选一种就行
- 其中k=3也好解释,
- 消费可以分为高消费、中消费、低消费
- 这里写在论文中可以辅助确定k值,还是有一定意义的
解释:
(1)根据聚合系数折线图可知,当类别数为5时,折线的下降趋势趋缓,故可将类别数设定为5.
(2)从图中可以看出, K值从1到5时,畸变程度变化最大。超过5以后,畸变程度变化显著降低。因此肘部就是 K=5,故可将类别数设定为5.(当然,K=3也可以解释)
确定K后画图
演示一下怎么画图
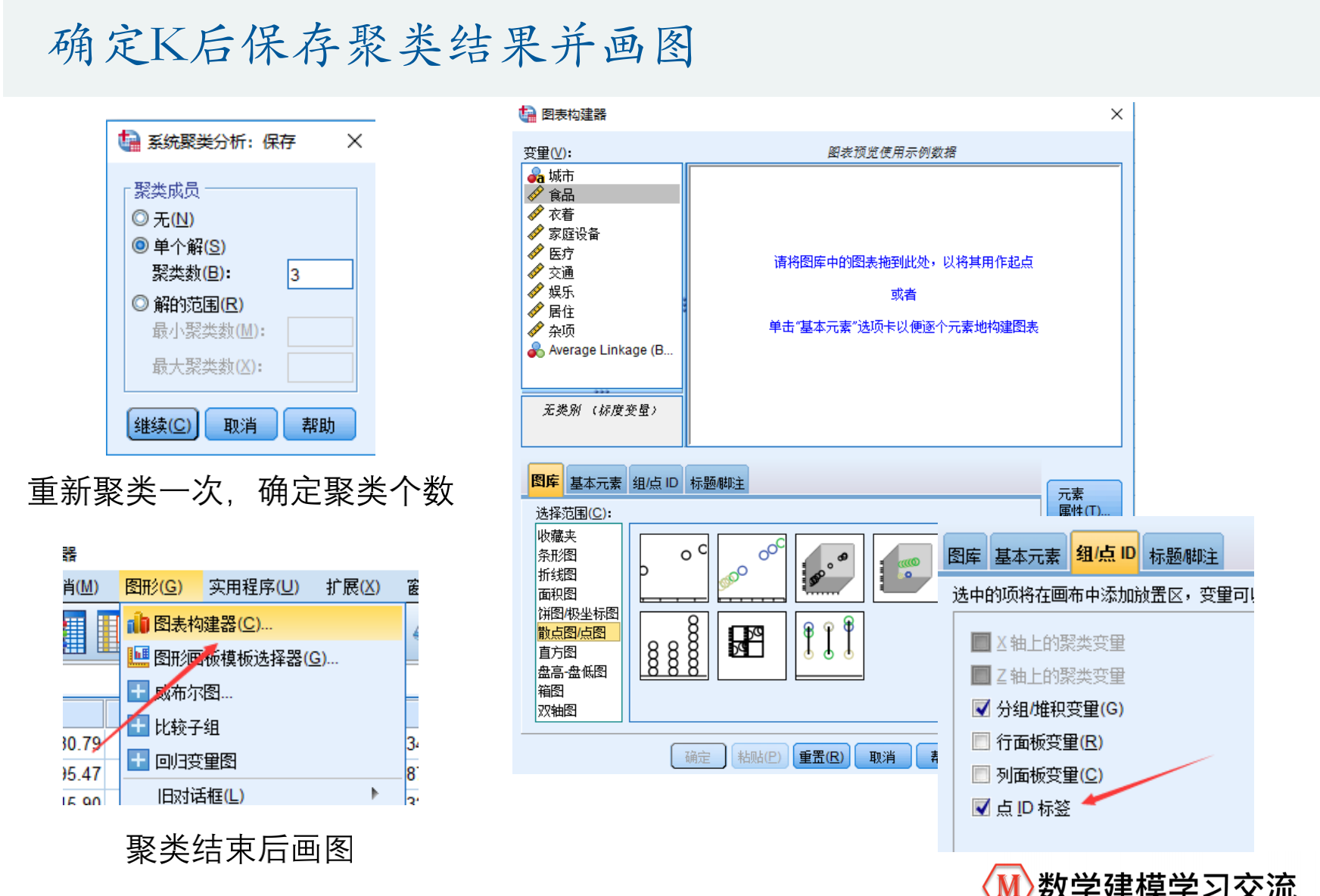

这里8个指标肯定画不了,只是演示一下2或3个指标怎么画
spss->图形-> 图表构造器
把图 指标拖进去
组合点( 勾选可以加一个点标签)
其他可以双击图进行修改,比如修改点颜色、背景颜色(填充改白色)、边框(黑色)、文本说明(右上角:类别编号)
DBSCAN算法
演示
DBSCAN算法:具有噪声的机遇密度的聚类方法
k均值算法与系统聚类算法是基于距离的
而DBSACAN是基于密度的聚类算法

- 举个例子
- 上次用k-means算法对笑脸图做出来的聚类

- 用DBSCAN算法
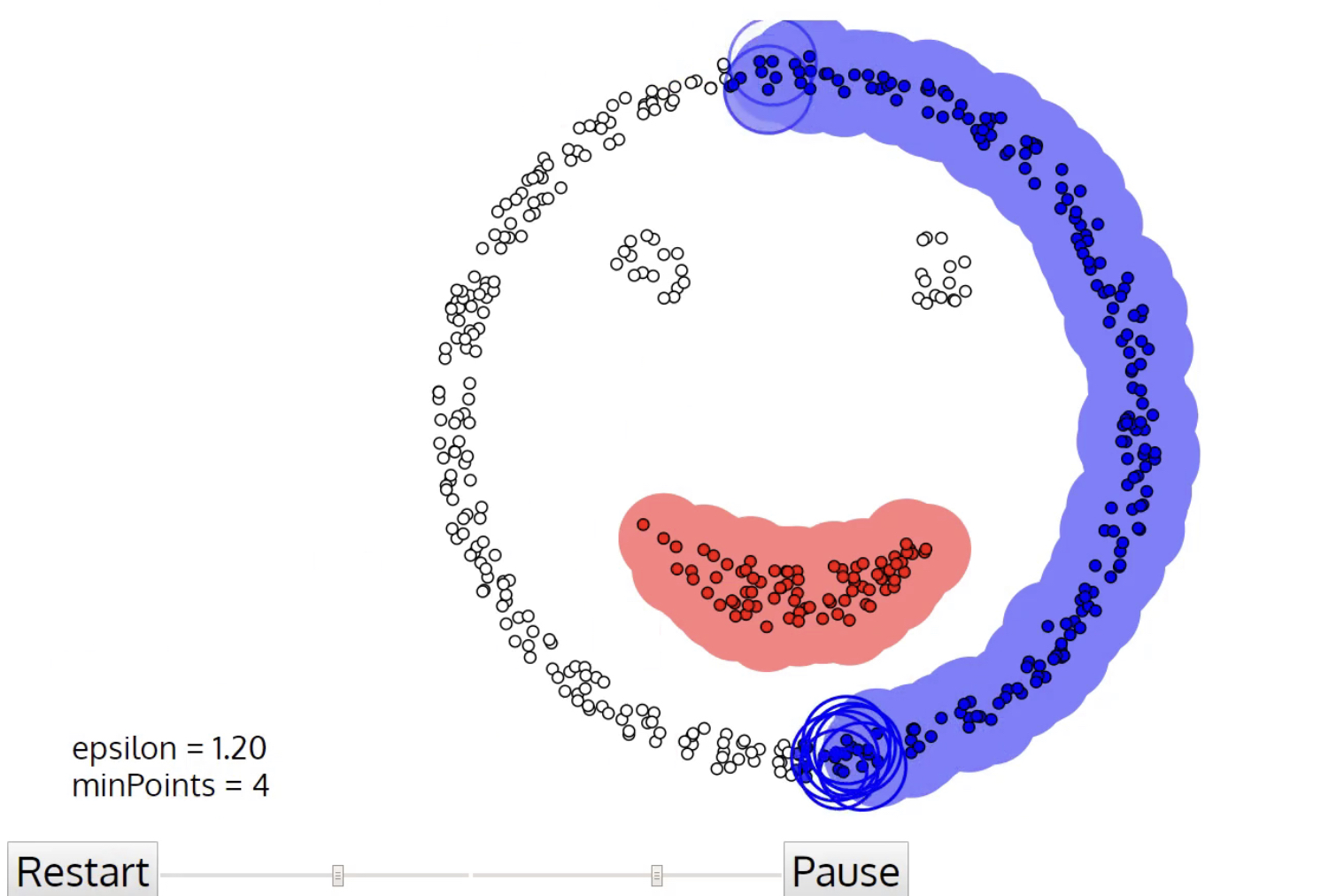
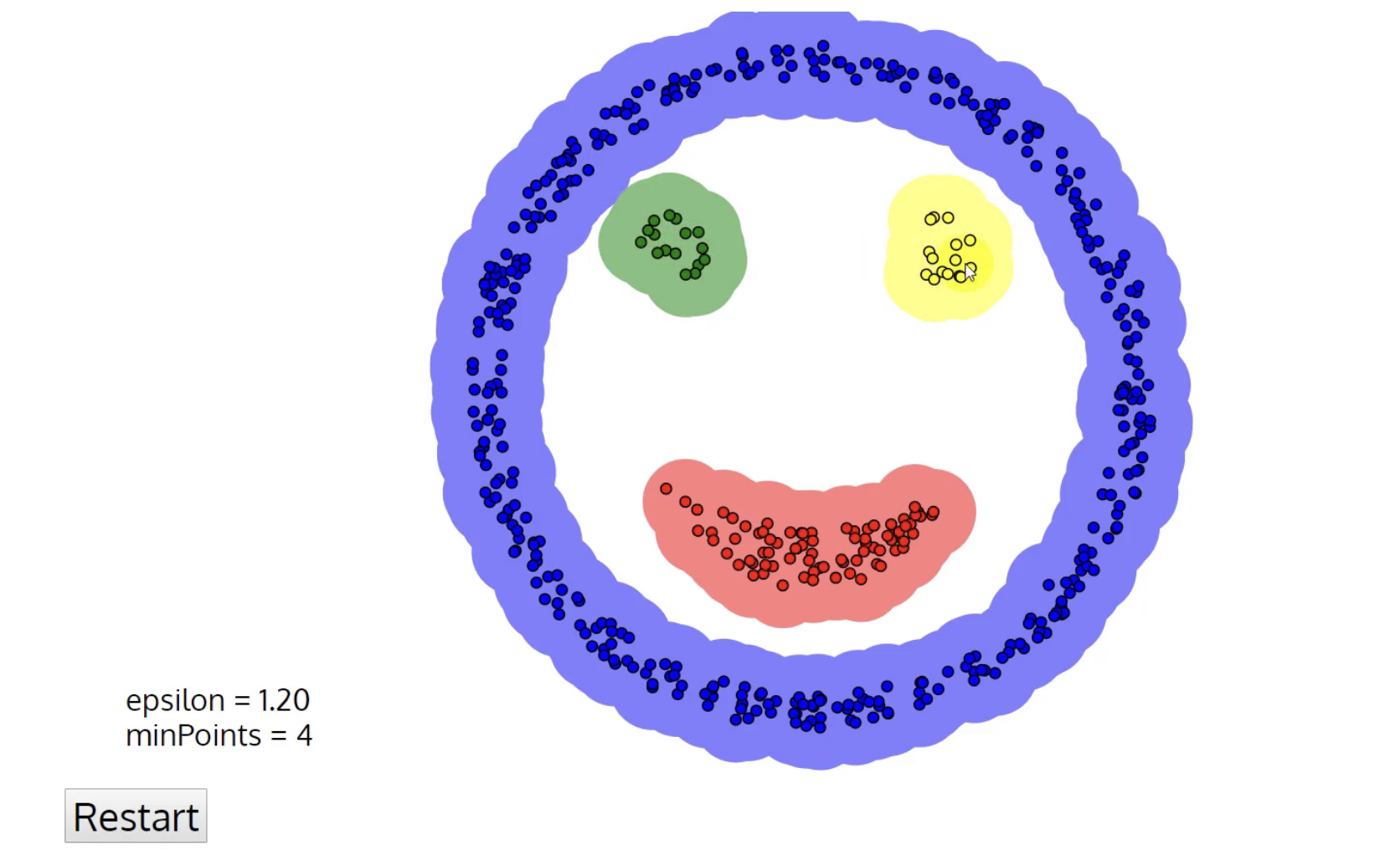
- 缩小DBSCAN算法搜索圈的半径
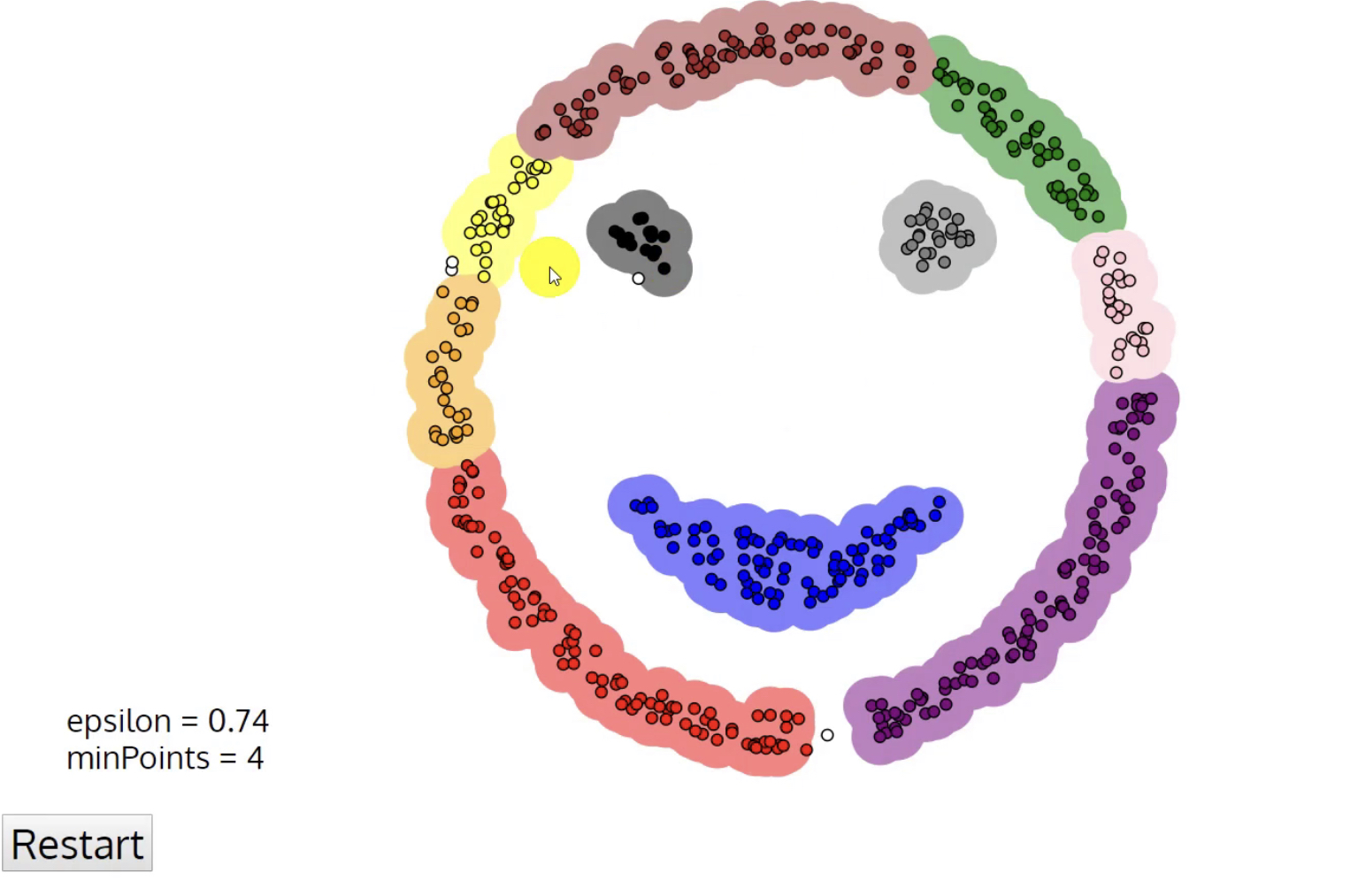
- 所以这个算法跟以下有关
- 数据
- 参数
- 可以发现噪声
- 比如类似验证码识别一样,聚类出来字母

基本概念
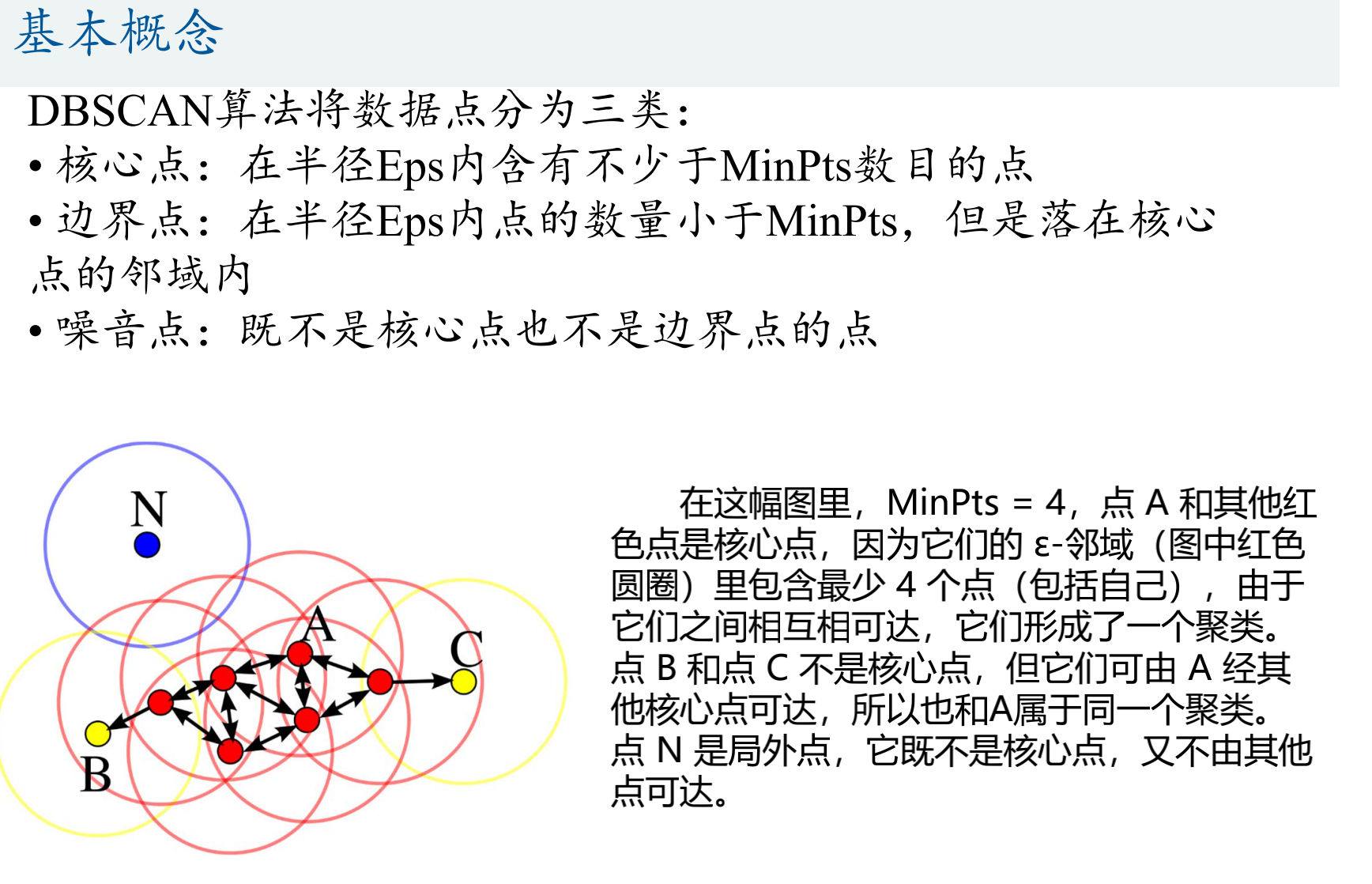
三类数据点
- 核心点:A
- 边界点:B、C
- 噪音点:N
所有的点都试探一遍
代码
- 伪代码形式

- matlab代码在资料中
%
% Copyright (c) 2015, Yarpiz (www.yarpiz.com)
% All rights reserved. Please read the "license.txt" for license terms.
%
% Project Code: YPML110
% Project Title: Implementation of DBSCAN Clustering in MATLAB
% Publisher: Yarpiz (www.yarpiz.com)
%
% Developer: S. Mostapha Kalami Heris (Member of Yarpiz Team)
%
% Contact Info: sm.kalami@gmail.com, info@yarpiz.com
%
function [IDX, isnoise]=DBSCAN(X,epsilon,MinPts)
C=0;
n=size(X,1);
IDX=zeros(n,1); % 初始化全部为0,即全部为噪音点
D=pdist2(X,X);
visited=false(n,1);
isnoise=false(n,1);
for i=1:n
if ~visited(i)
visited(i)=true;
Neighbors=RegionQuery(i);
if numel(Neighbors)<MinPts
% X(i,:) is NOISE
isnoise(i)=true;
else
C=C+1;
ExpandCluster(i,Neighbors,C);
end
end
end
function ExpandCluster(i,Neighbors,C)
IDX(i)=C;
k = 1;
while true
j = Neighbors(k);
if ~visited(j)
visited(j)=true;
Neighbors2=RegionQuery(j);
if numel(Neighbors2)>=MinPts
Neighbors=[Neighbors Neighbors2]; %#ok
end
end
if IDX(j)==0
IDX(j)=C;
end
k = k + 1;
if k > numel(Neighbors)
break;
end
end
end
function Neighbors=RegionQuery(i)
Neighbors=find(D(i,:)<=epsilon);
end
end
优缺点

- 就两个指标,画出散点图,发现可以分为几块,适合DBSCAN,一般用不到
- 其他的一般用系统聚类
- 可以写的东西多
- 树状图
- 肘部图折线图确定k值
课后作业

- 代码查重最好用的就是修改注释、修改变量名
本笔记来自清风老师的数学建模,强烈推荐该课程!