一、RNN（循环神经网络）介绍

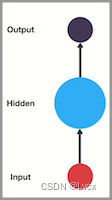
传统的神经网络的结构比较简单：输入层——隐藏层——输出层

RNN跟传统神经网络最大的区别在于，每次都会将前一次的输出结果带到下一次的隐藏层中，一起训练。如下图所示：
在这里插入图片描述

这里用一个具体的案例来看看RNN是如何工作的：
用户说了一句“what time is it？”，我们的神经网络会将这句话分成五个基本单元（十个单词+一个问号）
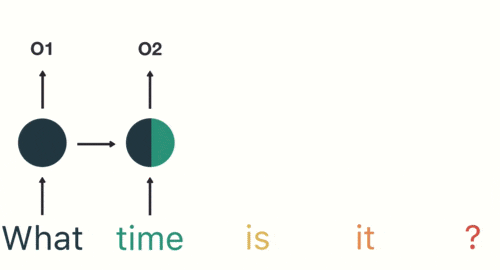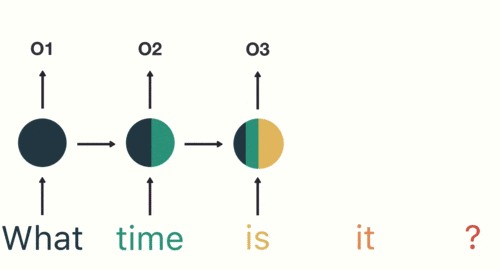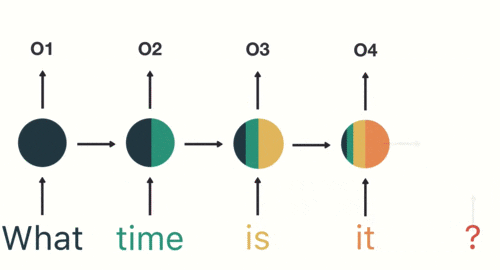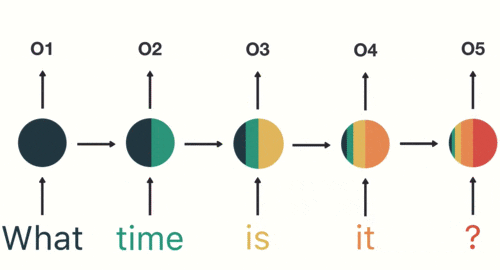
在这里插入图片描述

然后，按照顺序将五个基本单元输入RNN网络，先将“what”作为RNN的输入，得到01
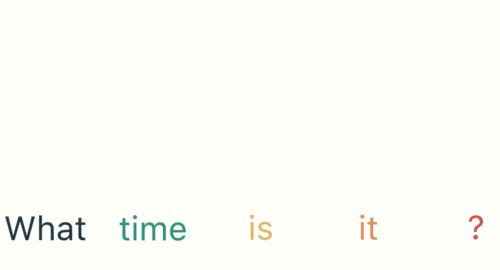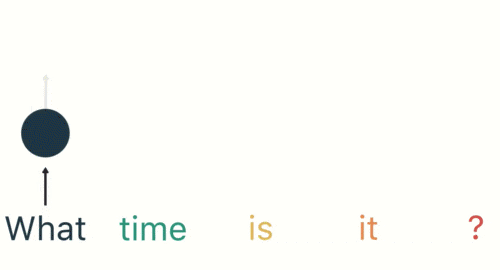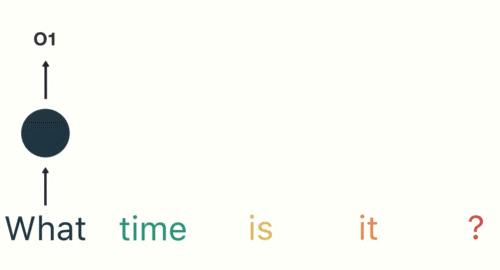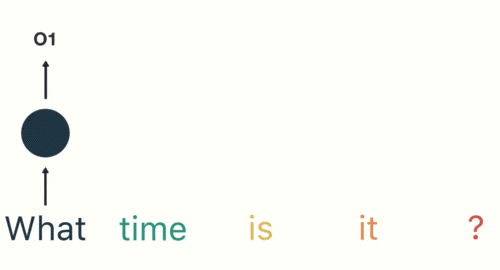
在这里插入图片描述

随后，按照顺序将“time”输入到RNN网络，得到02。

这个过程我们可以看到，输入“time”的时候，前面“what”的输出也会对02的输出产生了影响（隐藏层中有一半是黑色的）。
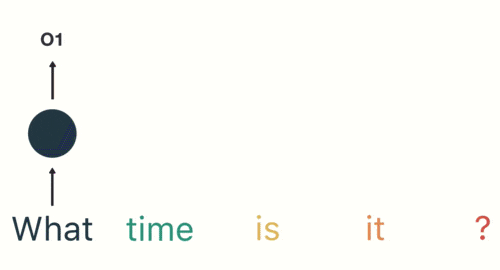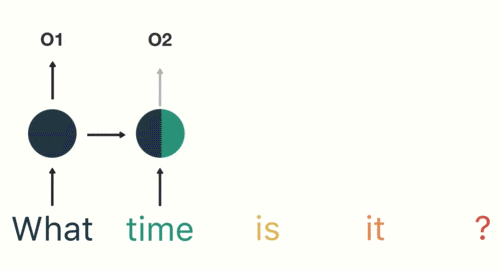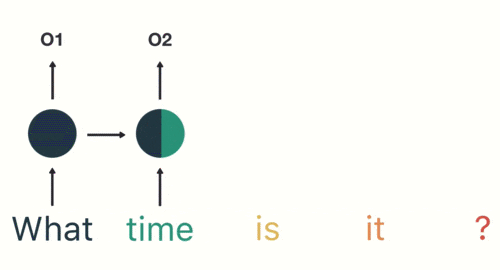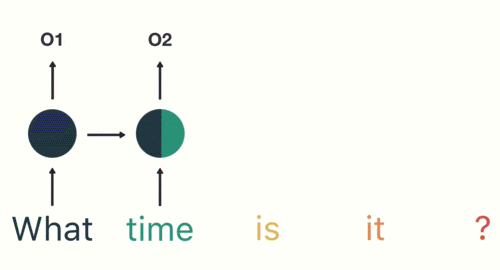
在这里插入图片描述

以此类推，我们可以看到，前面所有的输入产生的结果都对后续的输出产生了影响（可以看到圆形中包含了前面所有的颜色）
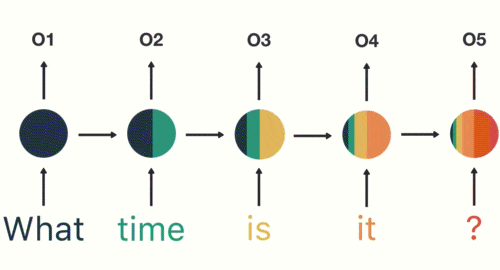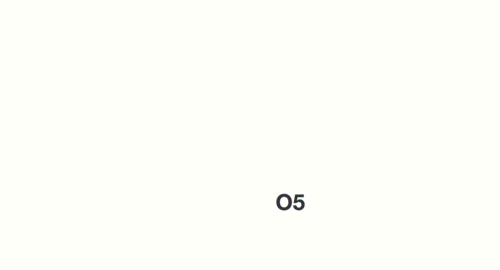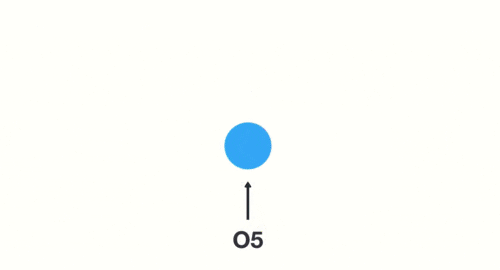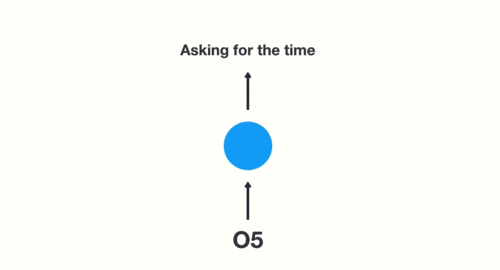
在这里插入图片描述

当神经网络判断亿图的时候，只需要最后一层的输出05即可，如下图所示：
在这里插入图片描述

二、准备工作

1. 设置GPU

如果使用的是CPU，可以不设置此部分。

import tensorflow as tf

gpus = tf.config.list_physical_devices("GPU")

if gpus:
    tf.config.experimental.set_memory_growth(gpus[0], True)   # 设置GPU显存按需使用
    tf.config.set_visible_devices([gpus[0]], "GPU")

2. 加载数据

import os, math
from tensorflow.keras.layers import Dropout, Dense, SimpleRNN
from sklearn.preprocessing import MinMaxScaler
from sklearn import metrics
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt

# 设置图表的显示支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']   # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False    # 用来正常显示负号

data = pd.read_csv('./datasets/SH600519.csv')   # 读取股票文件

data

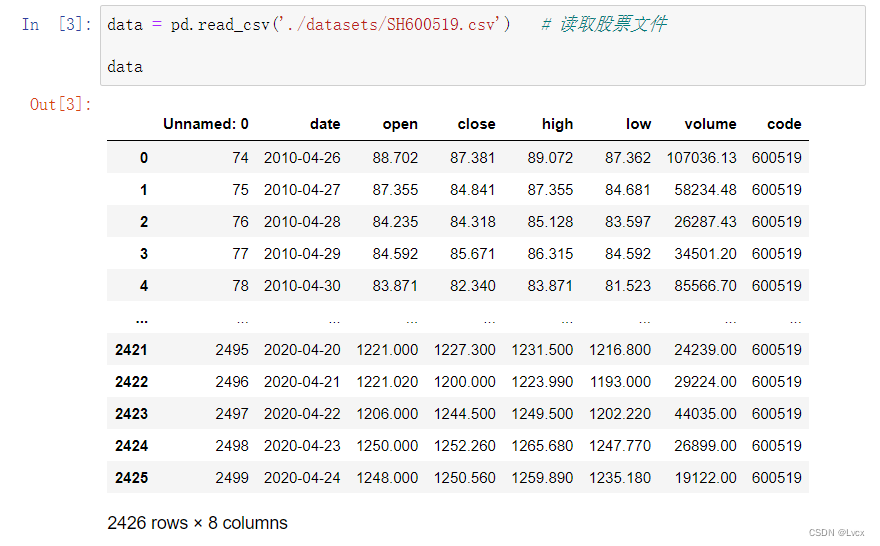
在这里插入图片描述

# 前（2426-300=2126）天的开盘价作为训练集，表格从0开始计数
# 2:3是提取[2:3)列，左闭右开
# 最后300天的开盘价作为测试集
training_set =data.iloc[0: 2426 - 300, 2: 3].values
test_set = data.iloc[2426-300: , 2: 3].values

三、数据预处理

1. 归一化

sc = MinMaxScaler(feature_range=(0, 1))
training_set = sc.fit_transform(training_set)
test_set = sc.transform(test_set)

2. 设置测试集和训练集

x_train = []
y_train = []

x_test = []
y_test = []

# 使用前60天的开盘价作为输入特征x_train
# 第61天的开盘价作为输入标签y_train
# for循环共构建2426-300-60=2066组训练数据
# 共构建300-60=260组测试数据

for i in range(60, len(training_set)):
    x_train.append(training_set[i - 60 : i, 0])
    y_train.append(training_set[i, 0])
    
for i in range(60, len(test_set)):
    x_test.append(test_set[i - 60 : i, 0])
    y_test.append(test_set[i, 0])
    

# 对训练集进行打乱
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)

# 将训练数据调整为数组
# 调整后的形状：
# x_train:(2066, 60, 1)
# y_train:(2066, )
# x_test:(240, 60, 1)
# y_test:(240, )

x_train, y_train = np.array(x_train), np.array(y_train)   
x_test, y_test = np.array(x_test), np.array(y_test)

# 输入要求：[送入样本数，循环核时间展开步数，每个时间步输入特征个数]
x_train = np.reshape(x_train, (x_train.shape[0], 60, 1))
x_test = np.reshape(x_test, (x_test.shape[0], 60, 1))

五、构建模型

model = tf.keras.Sequential([
    SimpleRNN(100, return_sequences=True),   # 布尔值。判断是返回输出序列中的最后一个输出，还是全部序列
    Dropout(0.1),   # 防止过拟合
    SimpleRNN(100),
    Dense(1)
])

六、激活模型

# 该应用只观测loss数值，不观测准确率，所以删去metrics选项，后面在每个epoch迭代显示时只显示loss值
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
             loss='mean_squared_error')   # 损失函数用均方误差

七、训练模型

history = model.fit(x_train, y_train,
                   batch_size=64,
                   epochs=35,
                   validation_data=(x_test, y_test),
                   validation_freq=1)    # 测试的epoch间隔数
model.summary()

Epoch 1/35
33/33 [==============================] - 1s 21ms/step - loss: 2.1443e-04 - val_loss: 0.0191
Epoch 2/35
33/33 [==============================] - 1s 20ms/step - loss: 1.7079e-04 - val_loss: 0.0180
Epoch 3/35
33/33 [==============================] - 1s 20ms/step - loss: 1.8806e-04 - val_loss: 0.0270
Epoch 4/35
33/33 [==============================] - 1s 21ms/step - loss: 1.8641e-04 - val_loss: 0.0212
Epoch 5/35
33/33 [==============================] - 1s 20ms/step - loss: 1.7237e-04 - val_loss: 0.0220
Epoch 6/35
33/33 [==============================] - 1s 20ms/step - loss: 1.9482e-04 - val_loss: 0.0214
Epoch 7/35
33/33 [==============================] - 1s 21ms/step - loss: 2.2625e-04 - val_loss: 0.0269
Epoch 8/35
33/33 [==============================] - 1s 21ms/step - loss: 1.8843e-04 - val_loss: 0.0318
Epoch 9/35
33/33 [==============================] - 1s 21ms/step - loss: 2.9509e-04 - val_loss: 0.0231
Epoch 10/35
33/33 [==============================] - 1s 21ms/step - loss: 2.5584e-04 - val_loss: 0.0126
Epoch 11/35
33/33 [==============================] - 1s 21ms/step - loss: 1.6293e-04 - val_loss: 0.0141
Epoch 12/35
33/33 [==============================] - 1s 21ms/step - loss: 1.8390e-04 - val_loss: 0.0147
Epoch 13/35
33/33 [==============================] - 1s 21ms/step - loss: 1.7752e-04 - val_loss: 0.0186
Epoch 14/35
33/33 [==============================] - 1s 21ms/step - loss: 2.1432e-04 - val_loss: 0.0205
Epoch 15/35
33/33 [==============================] - 1s 21ms/step - loss: 2.1611e-04 - val_loss: 0.0093
Epoch 16/35
33/33 [==============================] - 1s 20ms/step - loss: 2.0771e-04 - val_loss: 0.0245
Epoch 17/35
33/33 [==============================] - 1s 21ms/step - loss: 2.5106e-04 - val_loss: 0.0106
Epoch 18/35
33/33 [==============================] - 1s 21ms/step - loss: 1.9776e-04 - val_loss: 0.0173
Epoch 19/35
33/33 [==============================] - 1s 21ms/step - loss: 1.7719e-04 - val_loss: 0.0247
Epoch 20/35
33/33 [==============================] - 1s 21ms/step - loss: 2.1179e-04 - val_loss: 0.0298
Epoch 21/35
33/33 [==============================] - 1s 21ms/step - loss: 1.9824e-04 - val_loss: 0.0147
Epoch 22/35
33/33 [==============================] - 1s 21ms/step - loss: 2.0879e-04 - val_loss: 0.0260
Epoch 23/35
33/33 [==============================] - 1s 21ms/step - loss: 1.7415e-04 - val_loss: 0.0176
Epoch 24/35
33/33 [==============================] - 1s 21ms/step - loss: 1.6353e-04 - val_loss: 0.0090
Epoch 25/35
33/33 [==============================] - 1s 21ms/step - loss: 2.1351e-04 - val_loss: 0.0076
Epoch 26/35
33/33 [==============================] - 1s 21ms/step - loss: 1.7860e-04 - val_loss: 0.0170
Epoch 27/35
33/33 [==============================] - 1s 21ms/step - loss: 1.6161e-04 - val_loss: 0.0175
Epoch 28/35
33/33 [==============================] - 1s 21ms/step - loss: 1.5730e-04 - val_loss: 0.0108
Epoch 29/35
33/33 [==============================] - 1s 22ms/step - loss: 1.5606e-04 - val_loss: 0.0141
Epoch 30/35
33/33 [==============================] - 1s 22ms/step - loss: 1.7033e-04 - val_loss: 0.0119
Epoch 31/35
33/33 [==============================] - 1s 22ms/step - loss: 1.7409e-04 - val_loss: 0.0164
Epoch 32/35
33/33 [==============================] - 1s 21ms/step - loss: 1.6120e-04 - val_loss: 0.0168
Epoch 33/35
33/33 [==============================] - 1s 21ms/step - loss: 1.6100e-04 - val_loss: 0.0238
Epoch 34/35
33/33 [==============================] - 1s 21ms/step - loss: 1.5991e-04 - val_loss: 0.0299
Epoch 35/35
33/33 [==============================] - 1s 21ms/step - loss: 1.8989e-04 - val_loss: 0.0176
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
simple_rnn (SimpleRNN)       (None, 60, 100)           10200     
_________________________________________________________________
dropout (Dropout)            (None, 60, 100)           0         
_________________________________________________________________
simple_rnn_1 (SimpleRNN)     (None, 100)               20100     
_________________________________________________________________
dense (Dense)                (None, 1)                 101       
=================================================================
Total params: 30,401
Trainable params: 30,401
Non-trainable params: 0

八、结果可视化

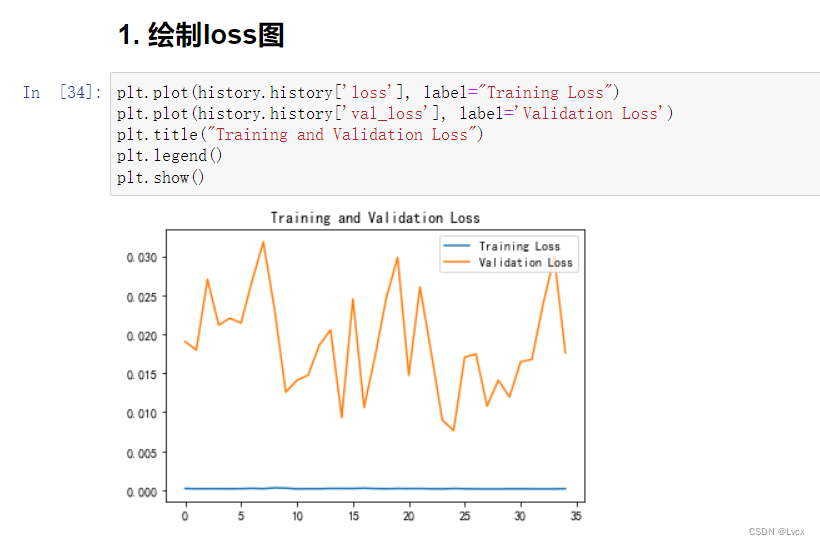
1. 绘制loss图

plt.plot(history.history['loss'], label="Training Loss")
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.title("Training and Validation Loss")
plt.legend()
plt.show()

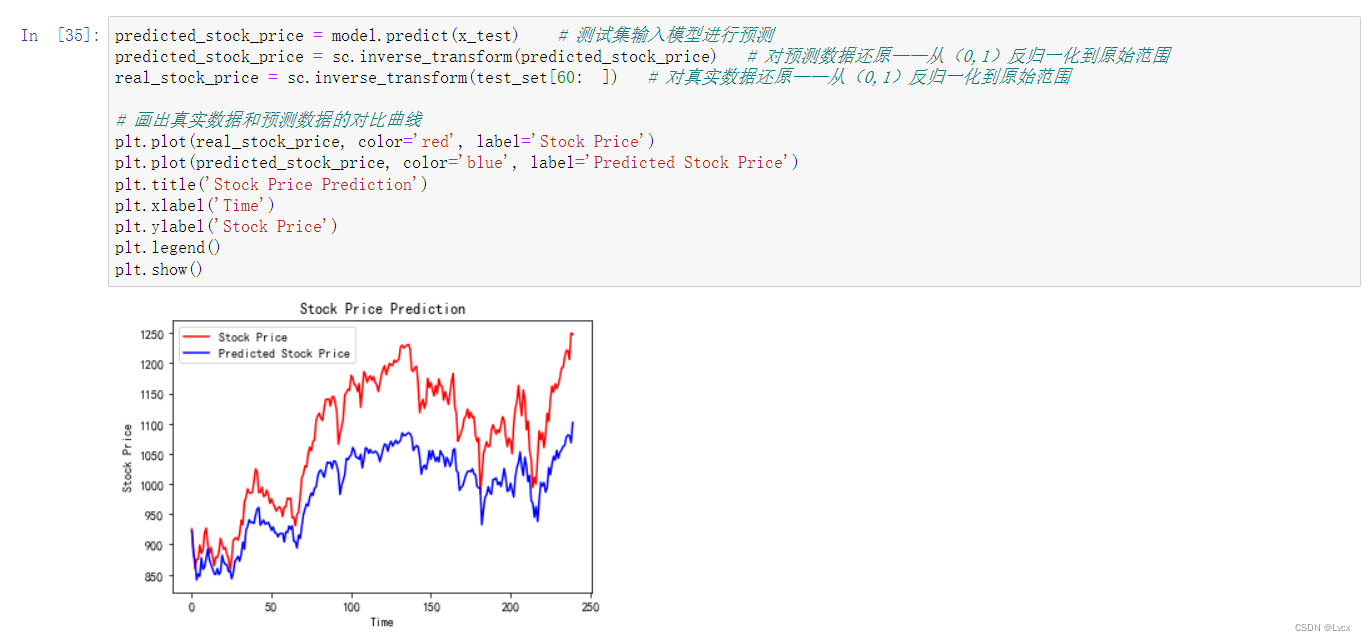
在这里插入图片描述

2. 预测

predicted_stock_price = model.predict(x_test)    # 测试集输入模型进行预测
predicted_stock_price = sc.inverse_transform(predicted_stock_price)   # 对预测数据还原——从（0,1）反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:  ])   # 对真实数据还原——从（0,1）反归一化到原始范围

# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted Stock Price')
plt.title('Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Stock Price')
plt.legend()
plt.show()

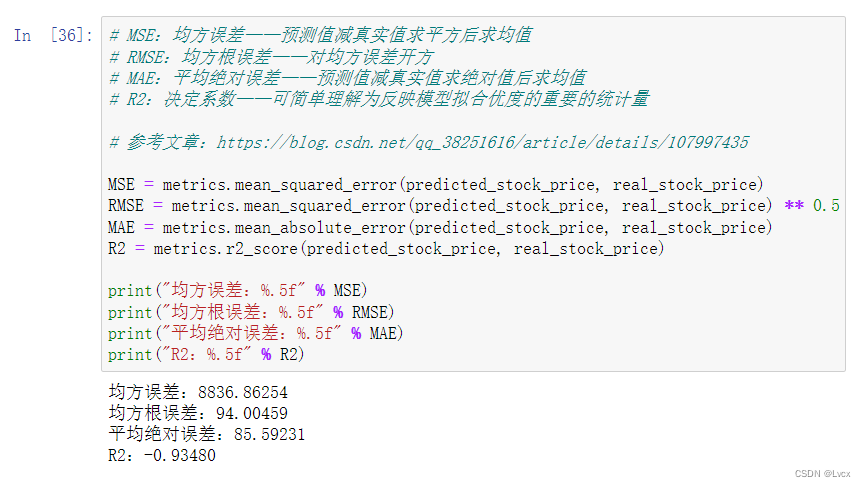
在这里插入图片描述

3. 评估

# MSE：均方误差——预测值减真实值求平方后求均值
# RMSE：均方根误差——对均方误差开方
# MAE：平均绝对误差——预测值减真实值求绝对值后求均值
# R2：决定系数——可简单理解为反映模型拟合优度的重要的统计量

# 参考文章：https://blog.csdn.net/qq_38251616/article/details/107997435

MSE = metrics.mean_squared_error(predicted_stock_price, real_stock_price)
RMSE = metrics.mean_squared_error(predicted_stock_price, real_stock_price) ** 0.5
MAE = metrics.mean_absolute_error(predicted_stock_price, real_stock_price)
R2 = metrics.r2_score(predicted_stock_price, real_stock_price)

print("均方误差：%.5f" % MSE)
print("均方根误差：%.5f" % RMSE)
print("平均绝对误差：%.5f" % MAE)
print("R2：%.5f" % R2)