
上篇文章介绍了MindSpore深度概率学习中的概率推断算法和概率模型,链接戳↓
本篇文章会介绍深度概率学习的第三部分:神经网络与贝叶斯神经网络,并在MindSpore上进行代码的实践。
3. 神经网络与贝叶斯神经网络
4. 贝叶斯应用工具箱

从神经网络讲起
说到神经网络想必大家都不陌生,下图就是一个典型的全连接神经网络,网络结构供四层(包括输入层和输出层),对应3个权重矩阵??,??和?。神经网络的训练过程就是调整三个权重矩阵的过程。
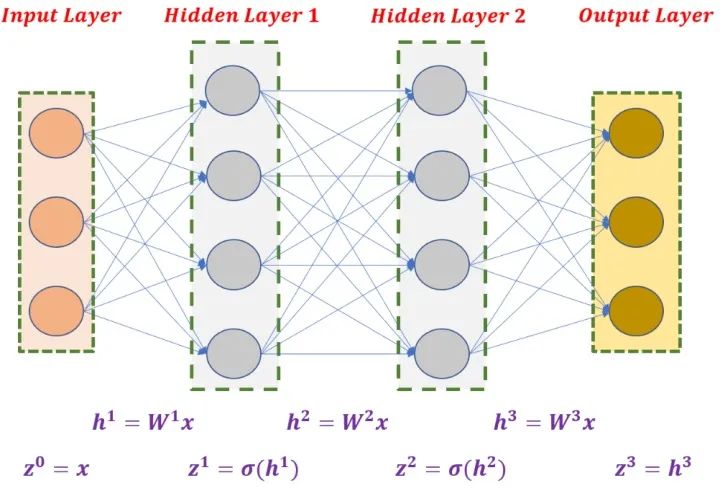
 ?
?
神经网络已经为许多机器学习和人工智能应用提供了最先进的结果,如图像分类、目标检测和语音识别等。
但是,由于神经网络是一个黑箱模型,人们难以理解它的内部工作机制和决策过程,因此很难证明黑箱模型的决策是正确的且难以控制和避免其异常行为,无法应用在自动驾驶和医疗决策等高风险领域。

什么是贝叶斯神经网络?
贝叶斯理论提供了一种自然的方法来解释预测中的不确定性,并且能够洞察这些决策是如何做出的。将贝叶斯理论和神经网络相结合得到的贝叶斯神经网络可以帮助我们解决神经网络目前面临的许多挑战。

从上图可以看出,贝叶斯神经网络与神经网络的不同之处在于,其权重参数是服从分布的随机变量,而不再是确定的值。
在贝叶斯神经网络的学习过程中,模型的权重参数是基于我们已知的和可以观察到的信息推导得到的。这是逆概率问题,可以利用贝叶斯定理加以求解。


变分推理?

这个目标函数可以分成两个部分:第一部分是变分后验与先验的KL散度,是复杂性代价,描述了权重和先验的契合程度;
第二部分的取值依赖于训练数据,是似然代价,描述对样本的拟合程度。然而这个目标函数还是无法求解的,接下来需要采用梯度下降和各种近似。

无偏蒙特卡罗梯度


高斯变分后验求解

?
因此,为了学习平均值和标准偏差,我们必须简单地计算通过反向传播发现的通常梯度,然后像上述步骤那样缩放和移动它们。
好了,贝叶斯神经网络的原理就介绍到这里,接下来就和大家介绍一下在MindSpore深度概率学习库中,我们如何来构造贝叶斯神经网络。

MindSpore实现
· 构造贝叶斯神经网络
MindSpore深度概率学习库中的:
mindspore.nn.probability.bnn_layer模块
提供了ConvReparam和DenseReparam两个接口,它们是基于上面介绍的Reparameterize方法实现的贝叶斯卷积层和全连接层。
利用bnn_layers模块中的ConvReparam和DenseReparam接口构建贝叶斯神经网络的方法与构建普通的神经网络相同。值得注意的是,bnn_layers中的ConvReparam和DenseReparam可以和普通的神经网络层互相组合。下面让我们看一下如何构建Bayesian LeNet。
import mindspore.nn as nn
from mindspore.nn.probability import bnn_layers
import mindspore.ops.operations as P
class BNNLeNet5(nn.Cell):
"""
bayesian Lenet network
Args:
num_class (int): Num classes. Default: 10.
Returns:
Tensor, output tensor
Examples:
>>> BNNLeNet5(num_class=10)
"""
def __init__(self, num_class=10):
super(BNNLeNet5, self).__init__()
self.num_class = num_class
self.conv1 = bnn_layers.ConvReparam(1, 6, 5, stride=1, padding=0, has_bias=False, pad_mode="valid")
self.conv2 = bnn_layers.ConvReparam(6, 16, 5, stride=1, padding=0, has_bias=False, pad_mode="valid")
self.fc1 = bnn_layers.DenseReparam(16 * 5 * 5, 120)
self.fc2 = bnn_layers.DenseReparam(120, 84)
self.fc3 = bnn_layers.DenseReparam(84, self.num_class)
self.relu = nn.ReLU()
self.max_pool2d = nn.MaxPool2d(kernel_size=2, stride=2)
self.flatten = nn.Flatten()
self.reshape = P.Reshape()
def construct(self, x):
x = self.conv1(x)
x = self.relu(x)
x = self.max_pool2d(x)
x = self.conv2(x)
x = self.relu(x)
x = self.max_pool2d(x)
x = self.flatten(x)
x = self.fc1(x)
x = self.relu(x)
x = self.fc2(x)
x = self.relu(x)
x = self.fc3(x)
return x贝叶斯神经网络的训练过程与DNN基本相同,唯一不同的是将WithLossCell替换为适用于BNN的WithBNNLossCell。
这是因为贝叶斯神经网络在优化是,不仅需要考虑损失函数,让网络的输出值尽可能接近真实值,还需要最小化贝叶斯层的KL散度。
除了backbone和loss_fn两个参数之外,WithBNNLossCell增加了dnn_factor和bnn_factor两个参数。
dnn_factor是由损失函数计算得到的网络整体损失的系数,bnn_factor是每个贝叶斯层的KL散度的系数,这两个参数是用来平衡网络整体损失和贝叶斯层的KL散度的,防止KL散度的值过大掩盖了网络整体损失。
# loss function definition
criterion = SoftmaxCrossEntropyWithLogits(sparse=True, reduction="mean")
# optimization definition
optimizer = AdamWeightDecay(params=network.trainable_params(), learning_rate=0.0001)
net_with_loss = bnn_layers.WithBNNLossCell(network, criterion, dnn_factor=60000, bnn_factor=0.000001)
train_bnn_network = TrainOneStepCell(net_with_loss, optimizer)
train_bnn_network.set_train()
train_set = create_dataset('./mnist_data/train', 64, 1)
test_set = create_dataset('./mnist_data/test', 64, 1)
epoch = 10
for i in range(epoch):
train_loss, train_acc = train_model(train_bnn_network, network, train_set)
valid_acc = validate_model(network, test_set)
print('Epoch: {} \tTraining Loss: {:.4f} \tTraining Accuracy: {:.4f} \tvalidation Accuracy: {:.4f}'.
format(i, train_loss, train_acc, valid_acc))完整代码可以复制下方链接转到浏览器观看:
https://gitee.com/mindspore/mindspore/tree/master/tests/st/probability/bnn_layers
· 神经网络“一键转换”贝叶斯神经网络
有没有同学不想了解贝叶斯的相关原理,却想尝试一下贝叶斯神经网络?MindSpore深度概率学习库提供了贝叶斯转换接口(mindspore.nn.probability.transform)支持神经网络模型一键转换成贝叶斯神经网络。APITransformToBNN主要实现了两个功能:模型级别的转换(transform_to_bnn_model)和层级的转换(transform_to_bnn_model)。
下面就让我们看看如何实现神经网络向贝叶斯神经网络的转换吧:
network = LeNet5()
# loss function definition
criterion = SoftmaxCrossEntropyWithLogits(sparse=True, reduction="mean")
# optimization definition
optimizer = AdamWeightDecay(params=network.trainable_params(), learning_rate=0.0001)
net_with_loss = WithLossCell(network, criterion)
train_network = TrainOneStepCell(net_with_loss, optimizer)
# transform the whole DNN modle to BNN
bnn_transformer = transforms.TransformToBNN(train_network, dnn_factor=1, bnn_factor=1)
train_bnn_network = bnn_transformer.transform_to_bnn_model()在调用TransformToBNN实现模型转换之后,只需要按照普通神经网络的训练方法进行训练即可。
如果只想要转换神经网络中指定类型的层,调用层级转换(transform_to_bnn_model)的功能即可:
train_bnn_network = bnn_transformer.transform_to_bnn_layer(nn.Dense, bnn_layers.DenseReparam)模型转换的完整代码可以复制下方链接转到浏览器观看:https://gitee.com/mindspore/mindspore/tree/master/tests/st/probability/transformsAn example of transforms
本篇文章就到这里啦,这次主要分享了贝叶斯神经网络的原理与实现,如果有不对之处欢迎大家批评指正哈。
参考文献
[1] Charles Blundell, Julien Cornebise, Koray Kavukcuoglu and Daan Wierstra, Weight Uncertainty in Neural Networks, In Proceedings of the 32nd International Conference on Machine Learning (ICML 2015), 2015.
[2] Ethan Goan, Clinton Fookes, Bayesian Neural Networks: An Introduction and Survey, Case Studies in Applied Bayesian Data Science: CIRM Jean-Morlet Chair: 45-87, 2020.
[3] Bayesian Neural Networks:贝叶斯神经网络
[4] 贝叶斯神经网络最新综述
[5]A Short Introduction to Bayesian Neural Networks