第四章
暂退法
当面对更多的特征而样本不足的时候,线性模型往往会过拟合。线性模型没有考虑特征之间的交互作用,对于每个特征,必须指定正或负的权重而忽略其他特征。即使我们拥有比特征更多的样本,深度神经网路也有可能过拟合。
暂退法在前向传播过程中,计算每一内部层的同时注入噪声(同时丢弃一些神经元),我们从表面上看是在训练过程中丢弃一些神经元,在整个训练过程的每一次迭代过程中,标准的暂退法包括在计算下一层之前将当前层中的一些节点置零。

无偏差的加入噪声,但是期望不变。将丢弃法直接作用在隐藏全连接层的输出上。丢弃概率是控制模型复杂度的超参数。暂退法可以避免过拟合,通常与控制权重向量的位数和大小结合使用的,暂退法仅在训练期间使用

代码实现
# 实现dropour_layer函数,该函数以dropout的概率丢弃张量输入X中的元素
import torch
from torch import nn
from d2l import torch as d2l
def dropout_layer(X,dropout):
assert 0 <= dropout <= 1
if dropout == 1:
# 返回全零
return torch.zeros_like(X)
if dropout == 0:
# 保持不变
return X
mask = (torch.rand(X.shape) > dropout).float()
# 重新缩放剩余部分
return mask * X/(1.0- dropout)
# 测试函数功能
X = torch.arange(16,dtype = torch.float32).reshape((2,8))
print(X)
print(dropout_layer(X,0.))
print(dropout_layer(X,0.5))
print(dropout_layer(X,1.))
输出:
tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
[ 8., 9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
[ 8., 9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0., 2., 0., 0., 8., 0., 12., 14.],
[ 0., 18., 20., 22., 24., 0., 28., 30.]])
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0.]])
# 定义有两个隐藏层的多层感知机,每个隐藏层包含256个单元
num_inputs,num_outputs,num_hiddens1,num_hiddens2 = 784,10,256,256
dropout1,dropout2 = 0.2,0.5
class Net(nn.Module):
def __init__(self,num_inputs,num_outputs,num_hiddens1,num_hiddens2,is_training= True):
super(Net,self).__init__()
self.num_inputs = num_inputs
self.training = is_training
# 两个隐藏层,三个线性层
self.lin1 = nn.Linear(num_inputs,num_hiddens1)
self.lin2 = nn.Linear(num_hiddens1,num_hiddens2)
self.lin3 = nn.Linear(num_hiddens2,num_outputs)
self.relu = nn.ReLU()
def forward(self,X):
# 第一个隐藏层
H1 = self.relu(self.lin1(X.reshape(-1,self.num_inputs)))
if self.training == True:
H1 = dropout_layer(H1,dropout1)
# 第二个隐藏层
H2 = self.relu(self.lin2(H1))
if self.training == True:
H2 = dropout_layer(H2,dropout2)
out = self.lin3(H2)
return out
net = Net(num_inputs,num_outputs,num_hiddens1,num_hiddens2)
# 训练和测试
num_epochs,lr,batch_size = 10,0.5,256
loss = nn.CrossEntropyLoss(reduction ='none')
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(),lr=lr)
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)
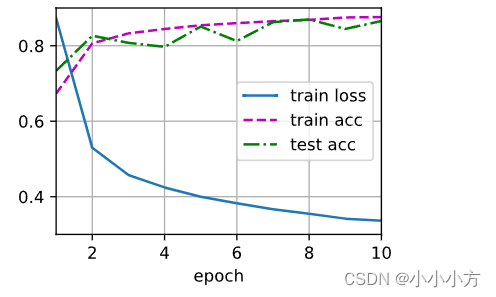
# 简洁实现
# 简洁实现
net = nn.Sequential(
nn.Flatten(),nn.Linear(784,256),nn.ReLU(),
nn.Dropout(dropout1),nn.Linear(256,256),nn.ReLU(),nn.Dropout(dropout2),nn.Linear(256,10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight,std =0.01)
net.apply(init_weights);
trainer = torch.optim.SGD(net.parameters(),lr=lr)
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)
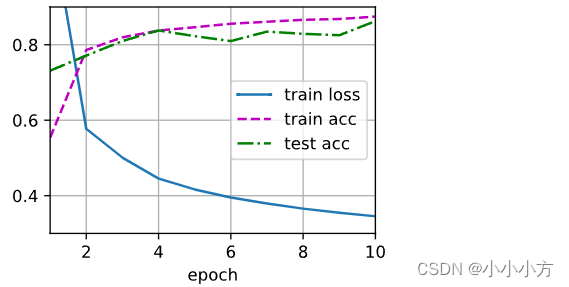
权重衰减
可以通过去收集更多训练数据来缓和过拟合,短期内不能完成。限制特征的数量是缓解过拟合的一种常用技术,简单的丢弃特征对于这项工作来说可能过于生硬。
在训练参数化机器学习模型时,权重衰减是最广泛使用的正则化技术之一,也被称为L2正则化,通过函数与零的距离来衡量函数的复杂度,要保证权重向量比较小,最常用的方法是将其范数作为惩罚项加到最小化损失问题中,将原来的训练目标最小化训练标签上预测损失,调整为最小化预测损失和惩罚项之和。

我们根据估计值和观测值之间的差异来更新W,同时也在考虑将W的大小缩小到0,仅考虑惩罚项,优化算法在训练的每一步衰减权重,为我们提供了一种连续的机制来调整函数的复杂度。
代码实现
# 权重衰减是最广泛使用的正则化的技术之一
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
# 生成数据集
# 选择的标签是关于输入的线性函数,标签被均值为0,标准差为0.01的噪声破坏
#将维数增加到200,使用20个样本的小训练集
# 模型越复杂数据越简单过拟合更容易发生
n_train,n_test,num_inputs,batch_size = 20,100,200,5
true_w,true_b = torch.ones((num_inputs,1))*0.01,0.05
# 数组变成iter
train_data = d2l.synthetic_data(true_w,true_b,n_train)
train_iter = d2l.load_array(train_data,batch_size)
test_data=d2l.synthetic_data(true_w,true_b,n_test)
test_iter = d2l.load_array(test_data,batch_size,is_train=False)
# 初始化模型参数
def init_params():
w = torch.normal(0,1,size=(num_inputs,1),requires_grad=True)
b = torch.zeros(1,requires_grad=True)
return [w,b]
# 定义L2惩罚 torch.abs(w)
def l2_penalty(w):
return torch.sum(w.pow(2))/2
# 定义训练代码实现 损失包含惩罚项
#超参数lambd
def train(lambd):
w,b=init_params()
# 线性网络和平凡损失没有变化所以直接进行导入
net,loss = lambda X:d2l.linreg(X,w,b),d2l.squared_loss
num_epochs,lr = 100,0.003
animator = d2l.Animator(xlabel = 'epoch',ylabel='loss',yscale='log',xlim=[5,num_epochs],legend=['trian','test'])
for epoch in range(num_epochs):
for X,y in train_iter:
# 变化:损失增加了L2范数惩罚项
# 广播机制使得l2_penalty(w)成为一个长度为batch_size的向量
l = loss(net(X),y)+lambd*l2_penalty(w)
l.sum().backward()
d2l.sgd([w,b],lr,batch_size)
if(epoch +1)%5==0:
animator.add(epoch+1,(d2l.evaluate_loss(net,train_iter,loss),d2l.evaluate_loss(net,test_iter,loss)))
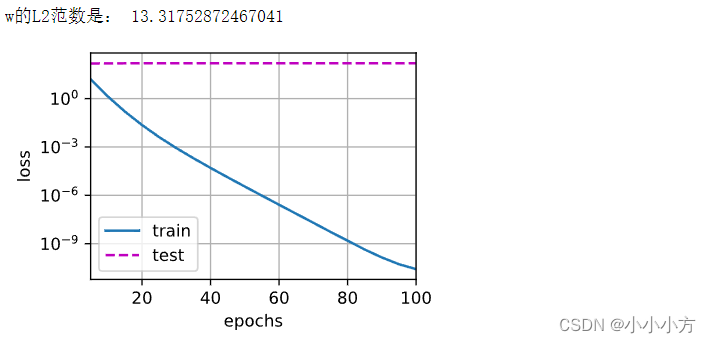
print('w的L2范数是:',torch.norm(w).item())
# 禁止使用权重衰减 训练误差有减少 但测试误差没有减少出现严重过拟合
train(lambd=0)
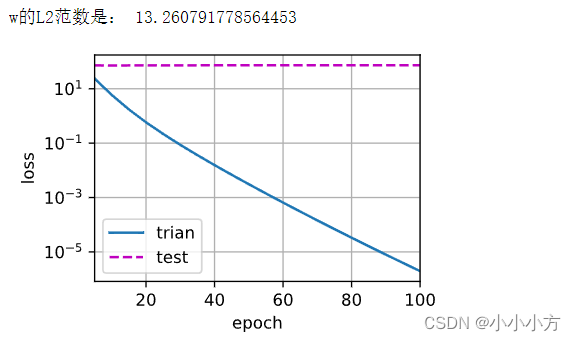
# 使用权重衰减,训练误差增大但测试误差减小 正则化缓解过拟合
train(lambd=3)
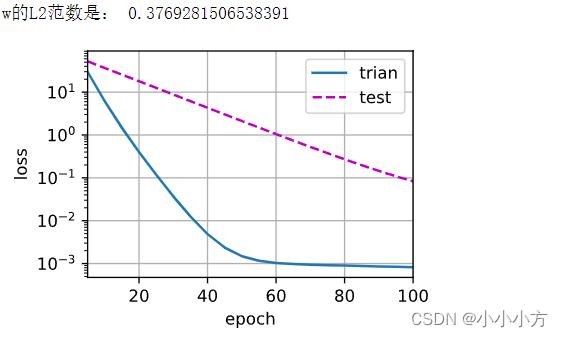
# 简洁实现 在实例化Trainer时直接通过wd指定wight decay超参数
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs,1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss()
num_epochs,lr = 100,0.003
trainer = torch.optim.SGD([{
'params':net[0].weight,
'weight_decay':wd},{'params':net[0].bias}
],lr=lr)
animator = d2l.Animator(xlabel='epochs',ylabel='loss',yscale='log',xlim=[5,num_epochs],legend=['train','test'])
for epoch in range(num_epochs):
for X,y in train_iter:
with torch.enable_grad():
trainer.zero_grad()
l=loss(net(X),y)
l.backward()
trainer.step()
if(epoch +1)%5==0:
animator.add(epoch+1,(d2l.evaluate_loss(net,train_iter,loss),d2l.evaluate_loss(net,test_iter,loss)))
print('w的L2范数是:',torch.norm(net[0].weight).item())
train_concise(0)
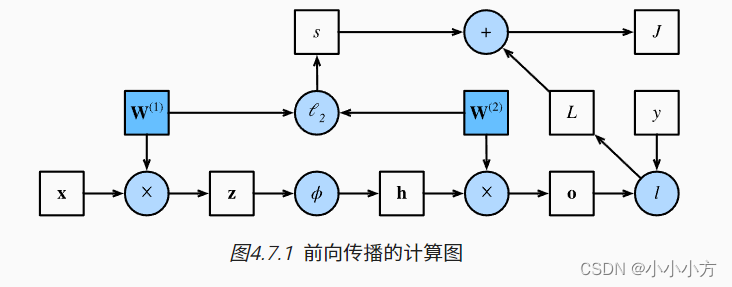
反向传播

梯度小事和梯度爆炸
初始化方案的选择在神经网络学习中起着举足轻重的作用,对保持参数稳定性至关重要。初始化方案的选择可以与非线性激活函数的选择结合在一起,糟糕的选择可能会导致我们在训练时遇到梯度爆炸或梯度消失。

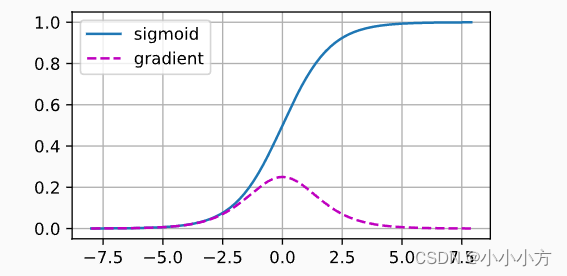
当sigmoid函数的输入很大或是很小的时候,梯度都会消失。


梯度消失问题对底层尤为严重,仅仅是顶层训练的比较好,无法让神经网络更深。数值太大或太小都会导致数值问题,为了让巡林更加稳定,应该让梯度值都在合理的范围内。方法包括:让乘法变成加法(ReSet和LSTM) 2.归一化:梯度归一化,梯度裁剪 3. 合理的初始化和激活函数。

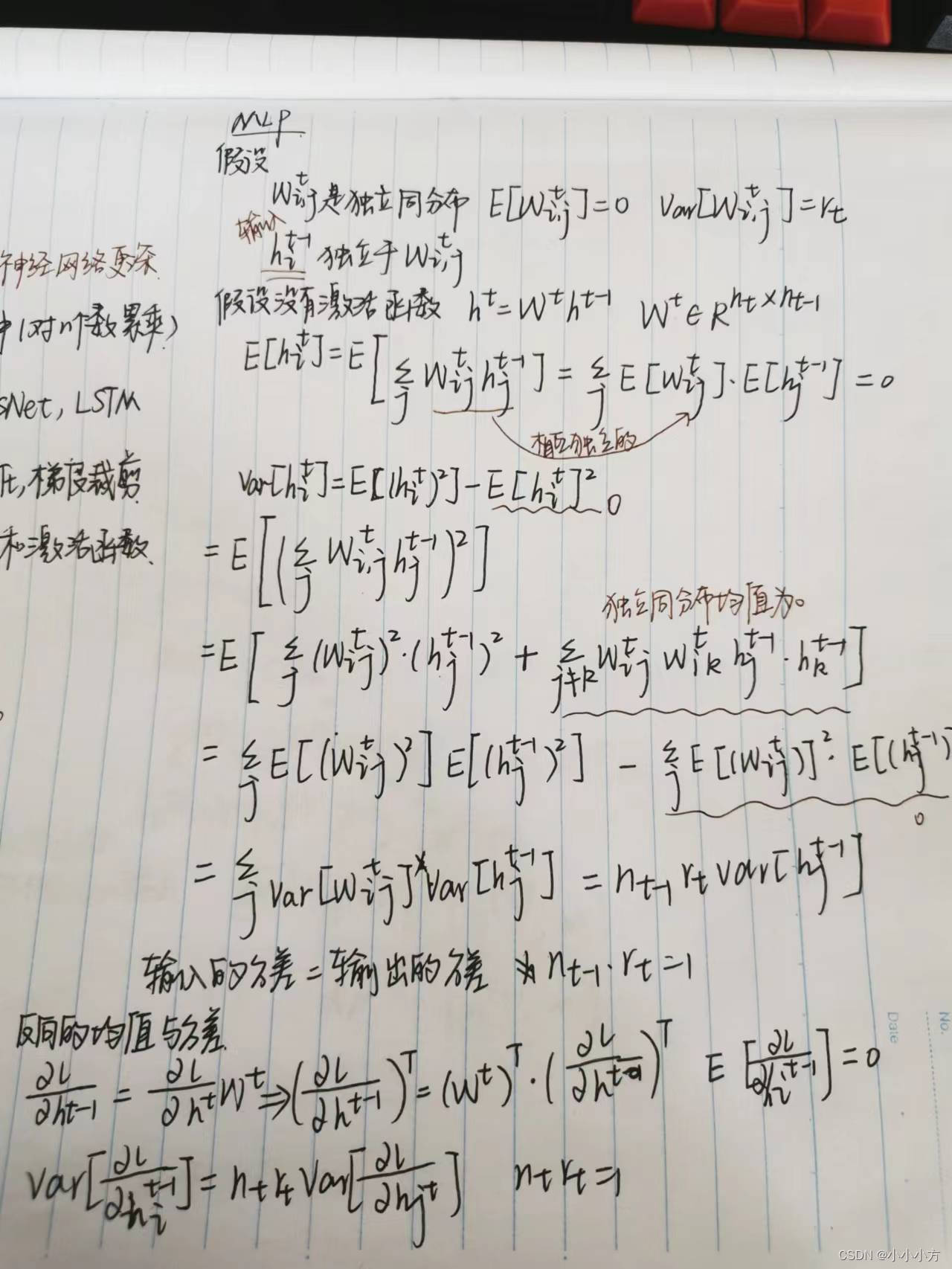

Kaggle比赛 预测房价
# 实现函数 方便下载数据
# 将数据集缓存在本地目录 默认../data 并返回下载文件的名称
import hashlib
import os
import tarfile
import zipfile
import requests
DATA_HUB = dict()
DATA_URL = 'http://d2l-data.s3-accelerate.amazonaws.com/'
def download(name,cache_dir=os.path.join('..','data')):
"""下载一个DATA_HUB中的文件,返回本地文件名"""
assert name in DATA_HUB, f"{name} 不存在于{DATA_HUB}."
url,shal_hash=DATA_HUB[name]
os.makedirs(cache_dir,exist_ok=True)
fname = os.path.join(cache_dir,url.split('/')[-1])
if os.path.exists(fname):
shal = hashlib.shal()
with open(fname,'rb')as f:
while True:
data = f.read(1048576)
if not data:
break
shal.update(data)
if shal.hexdigest() == shal_hash:
return fname
print(f'正在从{url}下载{fname}...')
r = requests.get(url,stream=True,verify=True)
with open(fname,'wb')as f:
f.write(r.content)
return fname
# 将下载并解压缩一个zip或tar文件
def download_extract(name,folder = None):
"""下载并解压zip或者tar文件"""
fname = download(name)
base_dir = os.path.dirname(fname)
data_dir,ext = os.path.splitext(fname)
if ext == '.zip':
fp = zipfile.ZipFile(fname,'r')
elif ext in ('.tar','.gz'):
fp = tarfile.open(fname,'r')
else:
assert False,'只有zip/tar文件可以被解压缩'
fp.extractall(base_dir)
return os.path.join(base_dir,folder) if folder else data_dir
# 将书本中使用的数据集DATA_HUB下载到缓存目录中
def download_all():
"""下载DATA_HUB中的所有文件"""
for name in DATA_HUB:
download(name)
%matplotlib inline
import pandas as pd
import numpy as np
import torch
from torch import nn
from d2l import mxnet as d2l
DATA_HUB['kaggle_house_train'] = (
DATA_URL +'kaggle_house_pred_train.csv',
'585e9cc93e70b39160e7921475f9bcd7d31219ce')
DATA_HUB['kaggle_house_test']=(
DATA_URL +'kaggle_house_pred_test.csv',
'fa19780a7b011d9b009e8bff8e99922a8ee2eb90')
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))
print(train_data.shape) #(1460,81)
print(test_data.shape) #(1459,80)
前4个特征和最后两个特征,以及相应标签
# 前4行 前4列后4列 iloc函数通过行号或者列号来读取数据
print(train_data.iloc[0:4,[0,1,2,3,-3,-2,-1]])
运行结果:
Id MSSubClass MSZoning LotFrontage SaleType SaleCondition SalePrice
0 1 60 RL 65.0 WD Normal 208500
1 2 20 RL 80.0 WD Normal 181500
2 3 60 RL 68.0 WD Normal 223500
3 4 70 RL 60.0 WD Abnorml 140000
第一个特征是ID,有助于模型识别每个训练样本,将数据提供给模型之前,将其从数据集中删除。
# 在每个样本中 第一个特征是ID,将其从数据集中删除
all_features = pd.concat((train_data.iloc[:,1:-1],test_data.iloc[:,1:]))
在开始建模之前,需要对数据进行预处理,将所有缺失的值替换为相应特征的平均值。通过将特征重新缩放到零均值和单位方差来标准化数据。
# 数值特征
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
# 对数值列 减去均值除以方差(均值为0 方差为1) 测试集和训练集一起做
all_features[numeric_features] = all_features[numeric_features].apply(lambda x:(x-x.mean())/(x.std()))
# 将缺失值变成0
all_features[numeric_features] = all_features[numeric_features].fillna(0)
# 处理离散值(字符串形式)使用独热编码替换 NA也会做出标记
all_features = pd.get_dummies(all_features,dummy_na = True)
all_features.shape
运行结果:
(2919, 331)
#从pandas格式中提取Numpy格式,并将其转换成张量表示
# 训练集个数
n_train = train_data.shape[0]
# 训练集特征
train_features = torch.tensor(all_features[:n_train].values,dtype=torch.float32)
# 测试集特征
test_features = torch.tensor(all_features[n_train:].values,dtype=torch.float32)
# 测试集标签,将1460 转换成[1460,1]
train_labels = torch.tensor(train_data.SalePrice.values.reshape(-1,1),dtype=torch.float32)
# 训练
loss = nn.MSELoss()
in_features = train_features.shape[1]
def get_net():
# 单层的线性回归 实例化nn
net = nn.Sequential(nn.Linear(in_features,1))
return net

# 使用相对误差来评估损失 一种方法是使用价格预测的对数来衡量误差
def log_rmse(net,features,labels):
# 将输入限制在一个范围内 并输出一个tensor
# 将小于1的值设置为1,使得取对数时数值更加稳定
clipped_preds = torch.clamp(net(features),1,float('inf'))
rmse = torch.sqrt(loss(torch.log(clipped_preds),torch.log(labels)))
return rmse.item()
# 训练函数借助Adam优化器 Adam是一种平滑的SGD对学习率没有那么敏感
def train(net, train_features, train_labels, test_features, test_labels,
num_epochs, learning_rate, weight_decay, batch_size):
# 训练损失,测试损失
train_ls, test_ls = [], []
# 加载数据
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)
# 这里使用了Adam优化算法
optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate, weight_decay=weight_decay)
# 进行迭代
for epoch in range(num_epochs):
for X, y in train_iter:
# 梯度清零
optimizer.zero_grad()
# 反向传播计算得到每个参数的梯度值
l=loss(net(X),y)
l.backward()
# 通过梯度下降执行一步参数更新
optimizer.step()
train_ls.append(log_rmse(net, train_features, train_labels))
if test_labels is not None:
test_ls.append(log_rmse(net, test_features, test_labels))
return train_ls, test_ls
# 使用一个K折交叉验证 返回一个训练集和一个验证集
def get_k_fold_data(k, i , X, y):
assert k>1
fold_size = X.shape[0] // k # 每个块的大小
X_train, y_train = None, None
for j in range(k):
idx = slice(j*fold_size, (j+1)*fold_size)
# 将第j个集合的特征和标签都放在part中
X_part, y_part = X[idx,:], y[idx]
# 如果当前的集合是第i折交叉验证,就将当前的集合当作验证模型
if j==i:
X_valid, y_valid = X_part, y_part
# 如果j!=i,x_train是空的直接将此部分放入训练集
elif X_train is None:
X_train, y_train = X_part, y_part
# j!=i 访问到了除了验证集其余集合的子集,放入训练集的集合
else:
X_train = torch.cat([X_train, X_part], 0)
y_train = torch.cat([y_train, y_part], 0)
return X_train, y_train, X_valid, y_valid
# 返回训练和验证误差的平均值
def k_fold( k, X_train, y_train, num_epochs,
learning_rate, weight_decay, batch_size ):
train_l_sum, valid_l_sum = 0,0
for i in range(k):
# 获得训练模型和第i个验证模型
data = get_k_fold_data(k, i, X_train, y_train)
net = get_net()
train_ls, valid_ls = train(net, *data, num_epochs, learning_rate,weight_decay, batch_size)
# 每一折的最后一次损失相加
train_l_sum += train_ls[-1]
valid_l_sum += valid_ls[-1]
if i==0:
d2l.plot(list(range(1, num_epochs + 1)), [train_ls, valid_ls],
xlabel='epoch', ylabel='rmse', xlim=[1, num_epochs],
legend=['train', 'valid'], yscale='log')
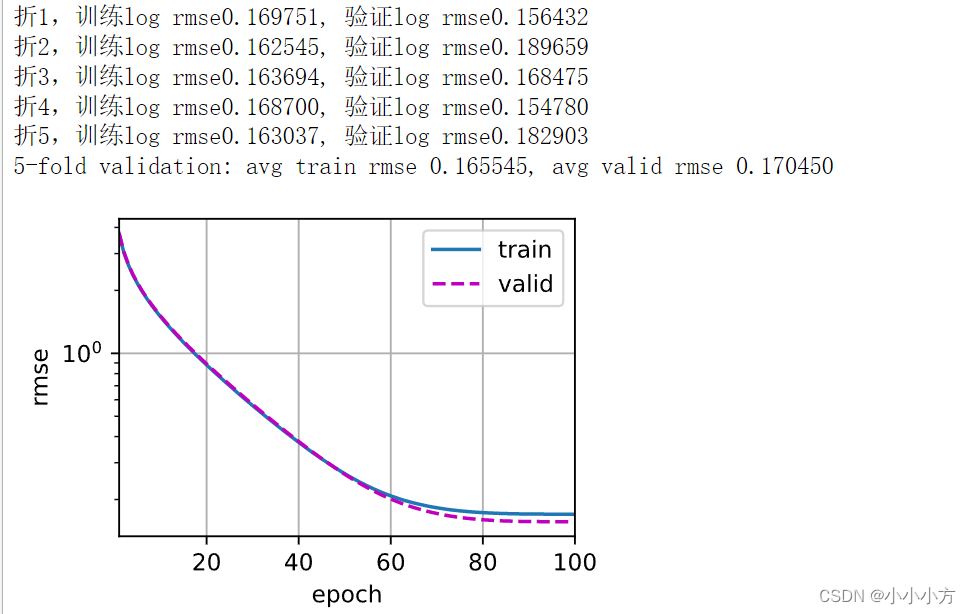
print(f'折{i + 1},训练log rmse{float(train_ls[-1]):f}, '
f'验证log rmse{float(valid_ls[-1]):f}')
return train_l_sum/k, valid_l_sum/k
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr, weight_decay, batch_size)
print('%d-fold validation: avg train rmse %f, avg valid rmse %f' % (k, train_l, valid_l))
# 定义预测函数,在预测之前 使用完整的训练数据集来重新训练模型,转换预测结果存成提交所需要的格式
def train_and_pred(train_features,test_features,train_labels,test_data,num_epochs,lr,weight_decay,batch_size):
# 获得net实例
net = get_net()
# 返回训练集损失
#_单个独立下划线是用作一个名字,来表示某个变量是临时的或者无关紧要的
train_ls,_ = train(net,train_features,train_labels,None,None,num_epochs,lr,weight_decay,batch_size)
# 作图
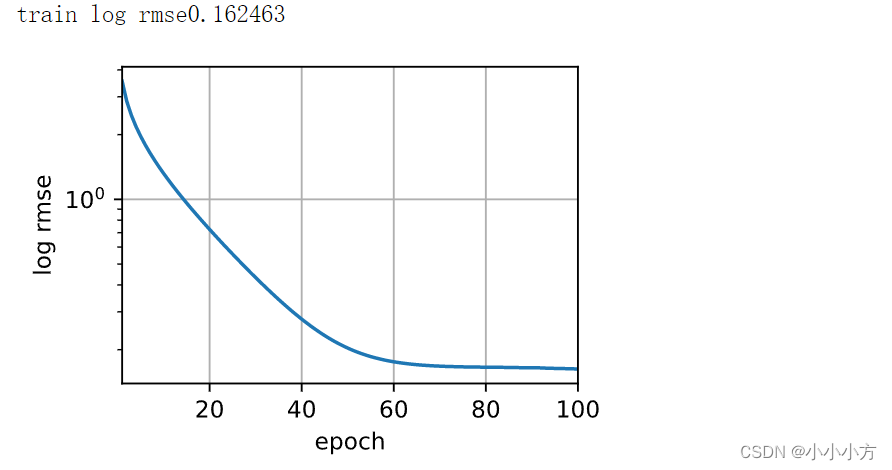
d2l.plot(np.arange(1,num_epochs+1),[train_ls],xlabel='epoch',ylabel='log rmse',xlim=[1,num_epochs],yscale='log')
print(f'train log rmse{float(train_ls[-1]):f}')
# 计算预测标签
# detach 返回一个新的tensor
preds = net(test_features).detach().numpy()
#SalePrice标签列
test_data['SalePrice'] = pd.Series(preds.reshape(1,-1)[0])
# 将测试集的Id和预测结果拼接在一起,axis沿水平方向拼接,与上面默认的纵向拼接不同
submission = pd.concat([test_data['Id'],test_data['SalePrice']],axis=1)
# 转成可提交的csv格式
submission.to_csv('submission.csv',index=False)
train_and_pred(train_features,test_features,train_labels,test_data,num_epochs,lr,weight_decay,batch_size)
深度学习计算
层和块
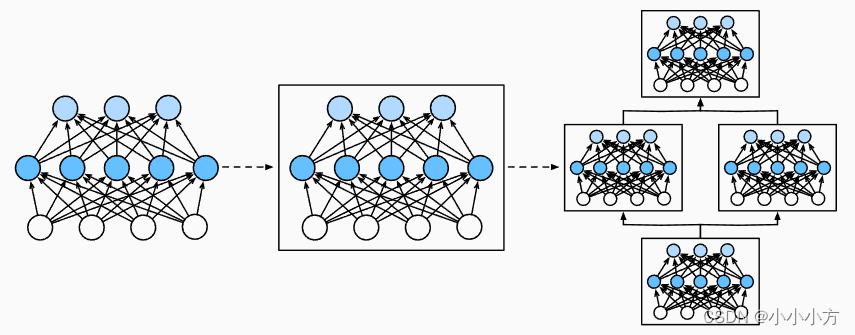
为了实现复杂的网络,我们引入了神经网络块的概念,块可以描述单个层、由多个层组成的组件或整个模型本身。使用块进行抽象的一个好处是可以将一些块组合成更大的组件,这一过程通常是递归的。
块由类表示,他的任何子类都必须定义一个将其输入转换成输出的前向传播函数,并且必须存储任何必须的参数,有些块不需要任何参数,为了计算梯度,块必须具有反向传播函数,block是表示块的类,维护block的有序列表。
# 多层感知机
import torch
from torch import nn
from torch.nn import functional as F
net = nn.Sequential(nn.Linear(20,256),nn.ReLU(),nn.Linear(256,10))
# 生成一个随机矩阵
X = torch.rand(2,20)
net(X)
运行结果:
tensor([[-0.1476, 0.1646, 0.2699, 0.2000, -0.6362, -0.3781, 0.0172, 0.1435,
-0.0330, -0.0155],
[-0.0021, 0.1729, 0.2095, 0.2067, -0.7153, -0.5767, 0.3187, 0.1717,
-0.0333, 0.1438]], grad_fn=<AddmmBackward0>)
# 自定义块
class MLP(nn.Module):
def __init__(self):
super().__init__()
# 定义两个全连接层,存在类的全连接变量中
self.hidden = nn.Linear(20,256)
self.out = nn.Linear(256,10)
def forward(self,X):
return self.out(F.relu(self.hidden(X)))
# 实例化多层感知机的层,在每次调用正向传播函数的时候调用这些层
net = MLP()
net(X)
运行结果:
tensor([[ 0.0668, 0.0370, 0.2017, -0.0594, -0.2957, 0.2299, 0.2208, 0.0746,
0.1747, 0.1283],
[-0.0311, 0.0540, 0.1961, -0.1322, -0.2300, 0.3730, 0.3043, 0.2021,
0.0114, 0.1557]], grad_fn=<AddmmBackward0>)
#Sequential的类是为了将其他模块串起来
# 定义两个关键函数 一个将块逐个添加到列表中的函数
# 一个前向传播函数 将输入按照追加块的顺序传递给块组成的链条
class MySequential(nn.Module):
def __init__(self,*args):
super().__init__()
for block in args:
# 系统会自动化_modules中的所有的成员
self._modules[block] = block
def forward(self,X):
for block in self._modules.values():
X = block(X)
return X
net = MySequential(nn.Linear(20,256),nn.ReLU(),nn.Linear(256,10))
net(X)
运行结果:
tensor([[ 0.0678, -0.2177, 0.0679, -0.2214, -0.0258, -0.1114, 0.1058, 0.1326,
-0.1481, -0.2392],
[ 0.0147, -0.2412, 0.0525, -0.0859, -0.0697, -0.2035, 0.0980, 0.1148,
-0.0744, -0.2046]], grad_fn=<AddmmBackward0>)
# 并不是所有的架构都是简单的顺序架构
# 当需要更强的灵活性时候,我们需要定义自己的块
# 有时我们可能需要合并一些常数参数
class FixedHiddenMLP(nn.Module):
def __init__(self):
super().__init__()
self.rand_weight = torch.rand((20,20),requires_grad = False)
self.linear = nn.Linear(20,20)
def forward(self,X):
X = self.linear(X)
X = F.relu(torch.mm(X,self.rand_weight)+1)
X = self.linear(X)
while X.abs().sum() >1:
X /= 2
return X.sum()
net = FixedHiddenMLP()
net(X)
运行结果:
tensor(-0.0173, grad_fn=<SumBackward0>)
# 混合搭配各种组合块 方法嵌套块
class NestMLP(nn.Module):
def __init__(self):
super().__init__()
self.net = nn.Sequential(nn.Linear(20,64),nn.ReLU(),
nn.Linear(64,32),nn.ReLU())
self.linear = nn.Linear(32,16)
def forward(self,X):
return self.linear(self.net(X))
chimera = nn.Sequential(NestMLP(),nn.Linear(16,20),FixedHiddenMLP())
chimera(X)
运行结果
tensor(-0.0561, grad_fn=<SumBackward0>)
一个块可以由许多层组成,一个块可以由许多块组成;块可以包含代码;块负责大量的内部处理,包括参数初始化和反向传播。
参数管理
设置超参数之后,就进入了训练阶段,我们的目标是找到使损失函数最小化的模型参数值,经过训练后,我们需要使用这些参数来做出未来预测,有时我们希望提取参数,以便在其他环境中复用他们,将模型保存下来,以便可以在其他软件中执行。
# 参数管理
# 单隐藏层MLP
import torch
from torch import nn
net = nn.Sequential(nn.Linear(4,8),nn.ReLU(),nn.Linear(8,1))
X = torch.rand(size=(2,4))
net(X)
运行结果:
tensor([[0.1304],
[0.0992]], grad_fn=<AddmmBackward0>)
# 拿出每一层中的权重
print(net[2].state_dict())
运行结果:
OrderedDict([('weight', tensor([[ 0.1283, 0.3211, -0.1503, -0.2624, -0.2783, 0.3022, -0.2113, 0.0045]])), ('bias', tensor([0.1943]))])
# 也可以直接访问某一个具体的参数
print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data)
运行结果:
<class 'torch.nn.parameter.Parameter'>
Parameter containing:
tensor([0.1943], requires_grad=True)
tensor([0.1943])
# 通过grad来访问他的梯度
net[2].weight.grad == None # True
# 一次性访问所有的参数
print(*[(name,param.shape) for name,param in net[0].named_parameters()])
print(*[(name,param.shape) for name,param in net.named_parameters()])
运行结果:
('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))
# 根据名称访问参数
net.state_dict()['2.bias'].data
运行结果:
tensor([0.1943])
# 从嵌套块收集参数
def block1():
return nn.Sequential(nn.Linear(4,8),nn.ReLU(),nn.Linear(8,4),nn.ReLU())
def block2():
net = nn.Sequential()
for i in range(4):
net.add_module(f'block{i}',block1())
return net
rgnet = nn.Sequential(block2(),nn.Linear(4,1))
rgnet(X)
运行结果:
tensor([[-0.3050],
[-0.3050]], grad_fn=<AddmmBackward0>)
# 查看内部的参数表示
print(rgnet)
运行结果:
Sequential(
(0): Sequential(
(block0): Sequential(
(0): Linear(in_features=4, out_features=8, bias=True)
(1): ReLU()
(2): Linear(in_features=8, out_features=4, bias=True)
(3): ReLU()
)
(block1): Sequential(
(0): Linear(in_features=4, out_features=8, bias=True)
(1): ReLU()
(2): Linear(in_features=8, out_features=4, bias=True)
(3): ReLU()
)
(block2): Sequential(
(0): Linear(in_features=4, out_features=8, bias=True)
(1): ReLU()
(2): Linear(in_features=8, out_features=4, bias=True)
(3): ReLU()
)
(block3): Sequential(
(0): Linear(in_features=4, out_features=8, bias=True)
(1): ReLU()
(2): Linear(in_features=8, out_features=4, bias=True)
(3): ReLU()
)
)
(1): Linear(in_features=4, out_features=1, bias=True)
)
深度学习框架提供默认随机初始化,也可以我们创建自定义初始化的方法。
# 内置初始化 m代表module
def init_normal(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight,mean=0,std=0.01)
nn.init.zeros_(m.bias)
#apply函数对net中的所有的层都进行遍历
net.apply(init_normal)
net[0].weight.data[0],net[0].bias.data[0]
运行结果:
(tensor([ 0.0150, 0.0048, -0.0048, -0.0180]), tensor(0.))
# 初始化成常量
def init_constant(m):
if type(m) == nn.Linear:
nn.init.constant_(m.weight,1)
nn.init.zeros_(m.bias)
net.apply(init_constant)
net[0].weight.data[0],net[0].bias.data[0]
运行结果:
(tensor([1., 1., 1., 1.]), tensor(0.))
# 对某些块应用不同的初始化方法
def xavier(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
def init_42(m):
if type(m) == nn.Linear:
nn.init.constant_(m.weight,42)
# 不同的层使用不同的初始化方法
net[0].apply(xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)
运行结果:
tensor([-0.3657, 0.6511, 0.6083, -0.0179])
tensor([[42., 42., 42., 42., 42., 42., 42., 42.]])
# 自定义初始化
def my_init(m):
if type(m) == nn.Linear:
print("Init",
*[(name,param.shape) for name,param in m.named_parameters()][0])
nn.init.uniform_(m.weight,-10,10)
# 保留绝对值大于5的权重
m.weight.data *= m.weight.data.abs() >= 5
net.apply(my_init)
net[0].weight[:2]
运行结果:
Init weight torch.Size([8, 4])
Init weight torch.Size([1, 8])
tensor([[ 0.0000, -8.7143, -6.0006, -0.0000],
[ 6.9307, -0.0000, -6.7732, -7.7121]], grad_fn=<SliceBackward0>)
# 直接设置参数
net[0].weight.data[:] += 1
net[0].weight.data[0,0] = 42
net[0].weight.data[0]
tensor([42.0000, -6.7143, -4.0006, 2.0000])
# 参数绑定 希望在多个层之间共享参数:定义一个稠密层,使用他的参数来设置另一个层的参数
shared = nn.Linear(8,8)
net = nn.Sequential(nn.Linear(4,8),nn.ReLU(),shared,nn.ReLU(),shared,nn.ReLU(),nn.Linear(8,1))
net(X)
print(net[2].weight.data[0] == net[4].weight.data[0])
net[2].weight.data[0,0] =100
print(net[2].weight.data[0] == net[4].weight.data[0])
运行结果:
# 第二层和第三层的参数是绑定的,不仅仅值相等,而且由相同的张量表示
tensor([True, True, True, True, True, True, True, True])
tensor([True, True, True, True, True, True, True, True])
```c
# 自定义一个层 也是nn.module的子类
# 构造一个没有任何参数的自定义层
import torch
import torch.nn.functional as F
from torch import nn
class CenteredLayer(nn.Module):
def __init__(self):
super().__init__()
def forward(self,X):
return X-X.mean()
layer = CenteredLayer()
layer(torch.FloatTensor([1,2,3,4,5]))
运行结果:
tensor([-2., -1., 0., 1., 2.])
# 自定义层与其他定义的module没有任何本质区别
# 将层作为组件合并到构建更复杂的模型中
net = nn.Sequential(nn.Linear(8,128),CenteredLayer())
Y = net(torch.rand(4,8))
Y.mean()
运行结果:
tensor(-2.7940e-09, grad_fn=<MeanBackward0>)
# 带参数的图层 参数都是parameter类的实例 使用parameter对参数进行处理
class MyLinear(nn.Module):
def __init__(self,in_units,units):
super().__init__()
self.weight = nn.Parameter(torch.randn(in_units,units))
self.bias = nn.Parameter(torch.randn(units,))
def forward(self,X):
linear = torch.matmul(X,self.weight.data)+self.bias.data
return F.relu(linear)
dense = MyLinear(5,3)
dense.weight
运行结果:
Parameter containing:
tensor([[-0.4619, 0.1590, -1.0537],
[-0.9483, 0.4736, -0.7941],
[-1.5670, 1.4901, -1.4020],
[-0.3832, 0.9105, 0.0649],
[-2.9608, -1.0028, 1.3522]], requires_grad=True)
# 使用自定义层直接进行前向传播计算
dense(torch.rand(2,5))
运行结果:
tensor([[0.0000, 0.8517, 1.0368],
[0.0000, 2.5194, 0.0000]])
# 使用自定义层构建模型
net = nn.Sequential(MyLinear(64,8),MyLinear(8,1))
net(torch.rand(2,64))
运行结果:
tensor([[5.5930],
[5.0809]])
读写文件
当运行一个耗时较长的训练过程时候,最佳的做法是定期保存中间结果,学习如何加载和存储权重向量和整个模型。
# 读写文件,如何加载和存储权重向量和整个模型
# 加载和保存张量 保存在当前目录中
import torch
from torch import nn
from torch.nn import functional as F
x = torch.arange(4)
torch.save(x,'x-file')
x2 = torch.load("x-file")
x2
运行结果:
tensor([0, 1, 2, 3])
# 存储一个张量列表 然后把它们都回内存
y = torch.zeros(4)
torch.save([x,y],'x-files')
x2,y2 = torch.load("x-files")
(x2,y2)
运行结果:
(tensor([0, 1, 2, 3]), tensor([0., 0., 0., 0.]))
# 写入或者读取从字符串映射到张量的字典
mydict = {'x':x,'y':y}
torch.save(mydict,'mydict')
mydict2 = torch.load('mydict')
mydict2
运行结果:
{'x': tensor([0, 1, 2, 3]), 'y': tensor([0., 0., 0., 0.])}
# 提供了内置函数来保存和加载整个网络
class MLP(nn.Module):
def __init__(self):
super().__init__()
self.hidden = nn.Linear(20,256)
self.output = nn.Linear(256,10)
def forward(self,x):
return self.output(F.relu(self.hidden(x)))
net = MLP()
X = torch.randn(size = (2,20))
Y = net(X)
# torch不存储整个模型的定义 存储网络的权重
# 将模型参数存储为一个叫做“mlp.params”的文件中
torch.save(net.state_dict(),'mlp.params')
# 为了恢复模型,实例化了一个原始多层感知机模型的备份,不需要随机初始化模型参数,直接读取文件中存储的参数
clone = MLP()
clone.load_state_dict(torch.load("mlp.params"))
clone.eval()
运行结果:
MLP(
(hidden): Linear(in_features=20, out_features=256, bias=True)
(output): Linear(in_features=256, out_features=10, bias=True)
)
# 验证
Y_clone = clone(X)
Y_clone == Y
运行结果:
tensor([[True, True, True, True, True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True]])