Backpropagation
引入话题
从前面的学习的梯度下降法我们可以知道：
参数的决定因素是上一个参数、学习率以及梯度，例如：
其中，梯度是个向量
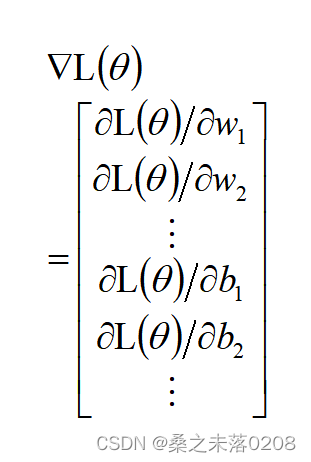
?那么如何有效得将百万维的向量计算出来，这时候我们就需要使用Backpropagation
所需的数学知识——链式法则
情况一：，
? ? ? ? ? ? ??
? ? ? ? ? ? ? 那么：
情况二：，
，
? ? ? ? ? ??
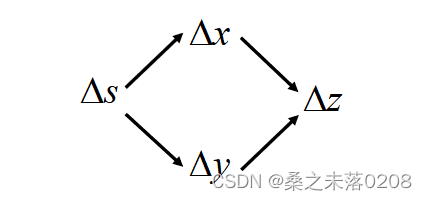
? ? ? ? ? ? 那么：?
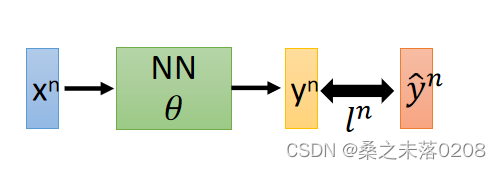
设置一个损失函数：，其中
表示
与
之间的距离，距离越大说明这个神经网络的参数值
不好。损失函数对某个参数
求微分是
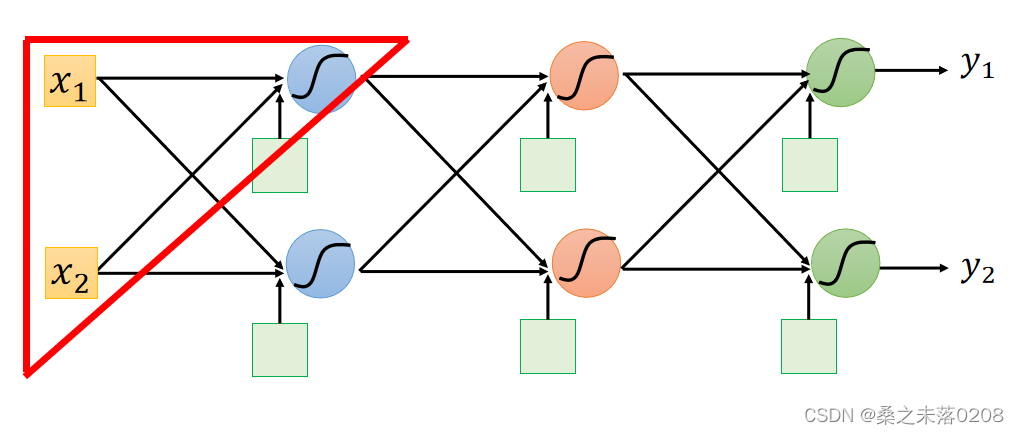
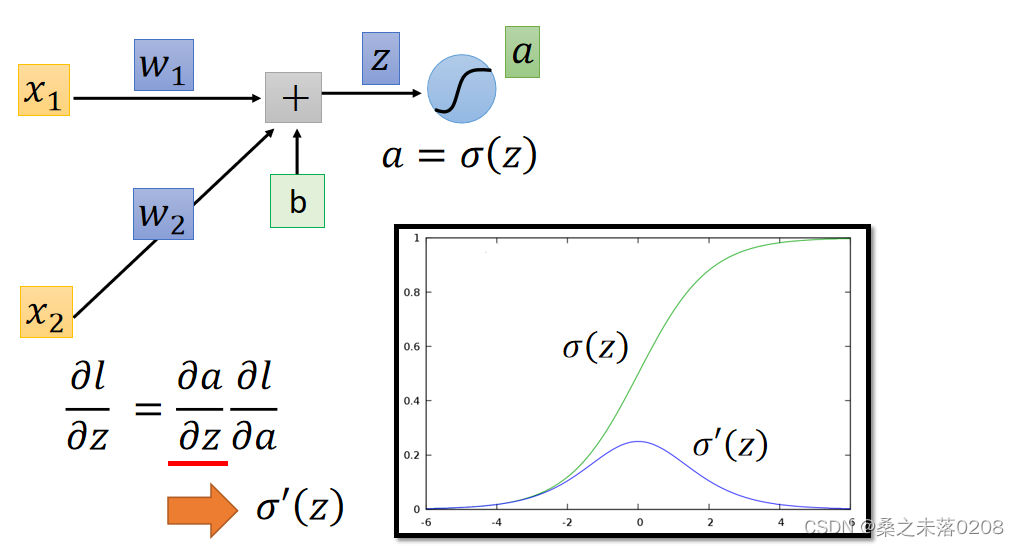
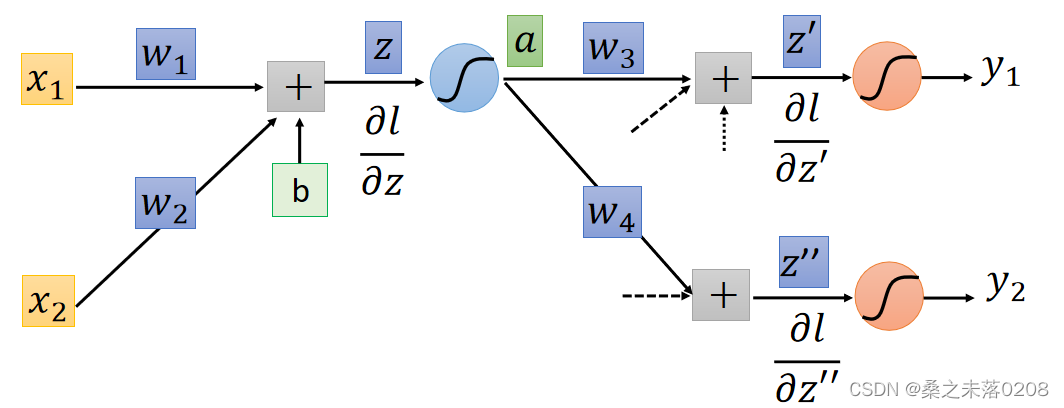
取神经网络中的一部分来说明：
?
?，
Forward pass和Backward pass
计算所有的参数的偏导数，叫做Forward pass，图如下：
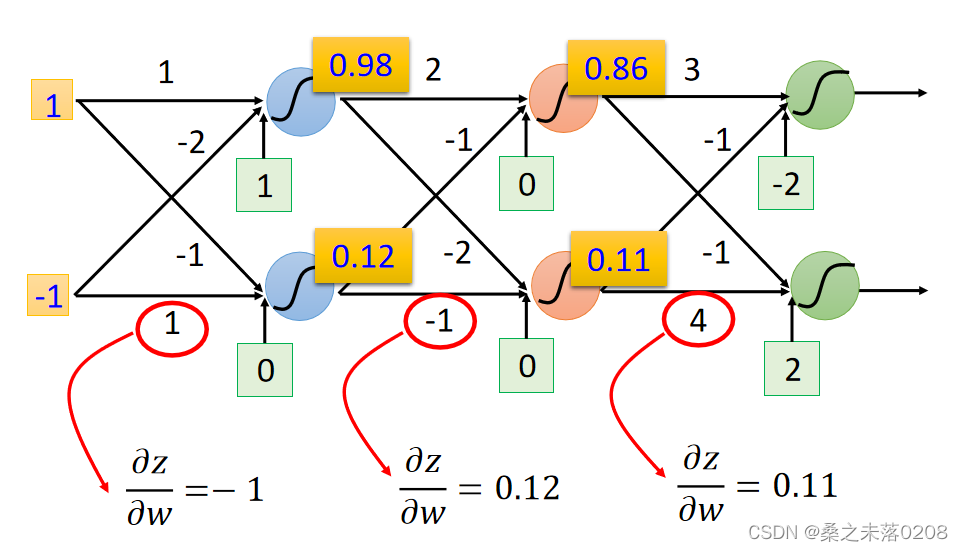
?计算所有激活功能输入值的偏导数，叫做Backward pass，图如下：
由于z在正向传递（ forward pass）中已经确定，所以是一个常数，所以上式就只有
和
是未知的。因此分情况讨论：
?情况一：红色圈圈位置就是输出层
?那么：，
，所以
和
求出来了。
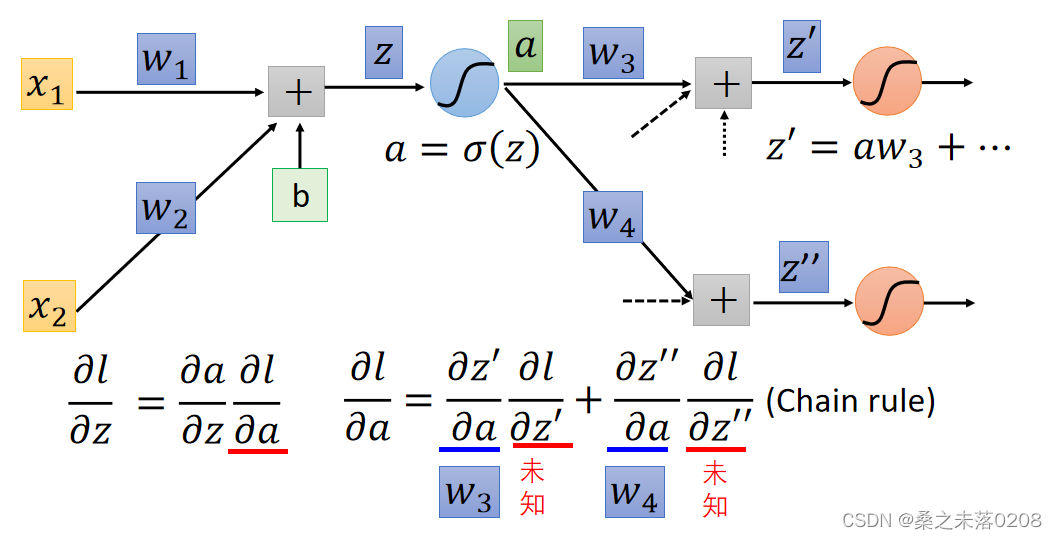
情况二：红色圈圈位置不是输出层
?利用递归的方法，直到找到输出层，从后向前偏导，拿下图举例：
已知了和
所以可以求得，以此向前类推，直到求得?
和
?。
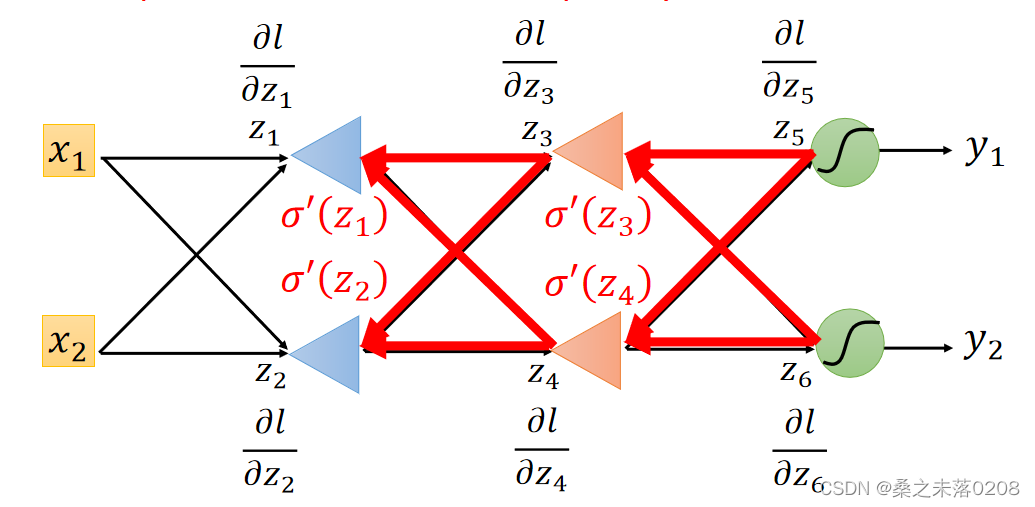
总结步骤：先求出Forward?pass，后求出Backward pass，两者相乘得出最终的某个参数的偏导数，进而求得损失函数。
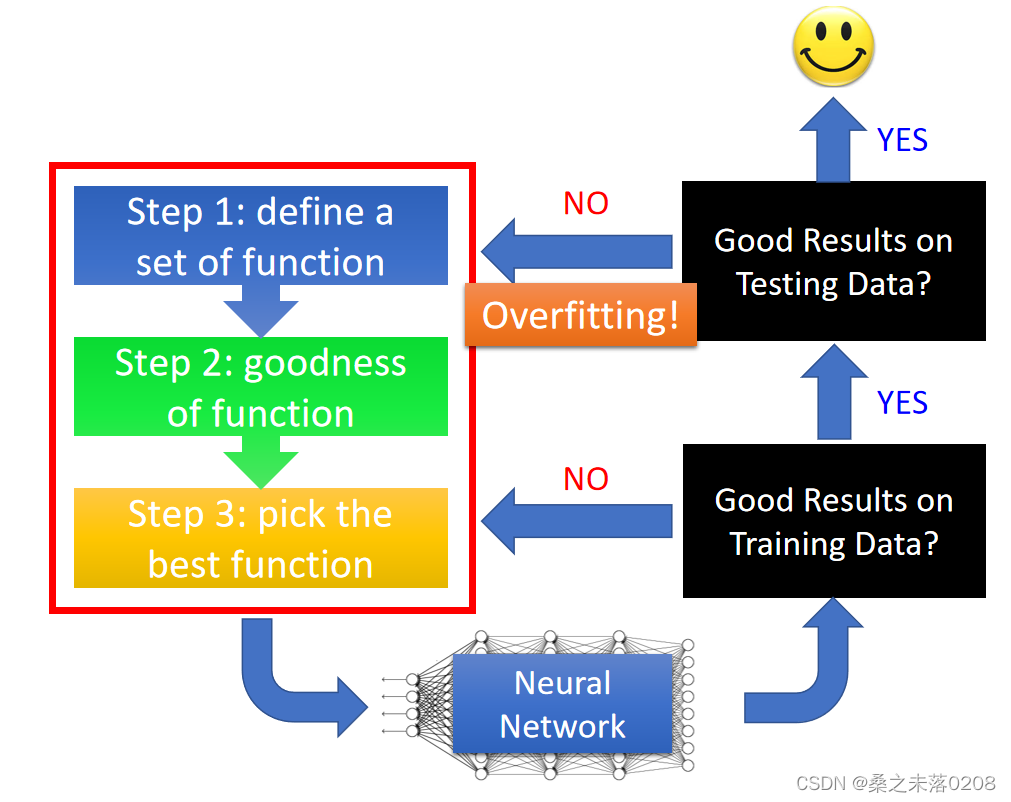
?Tips for Training DNN
深度学习的秘诀
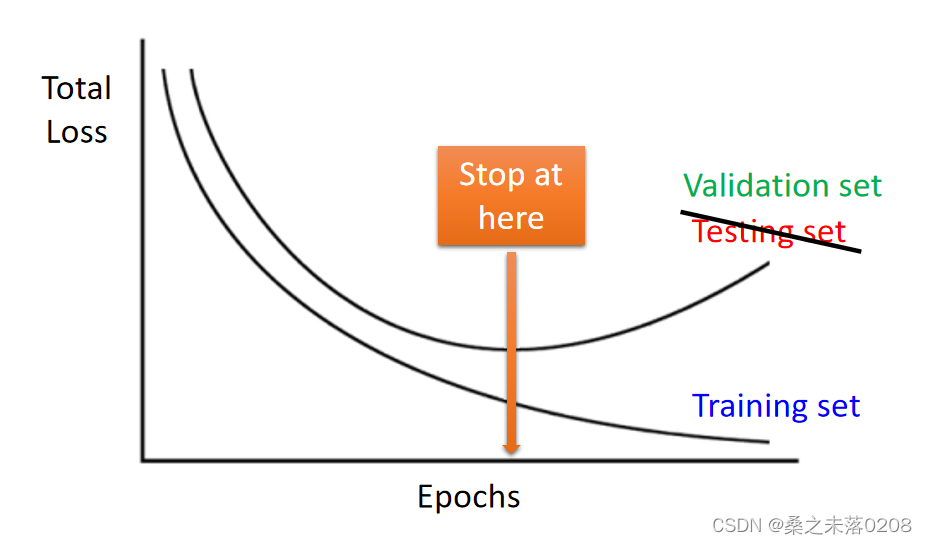
过拟合并非是我们面临的第一个问题，我们需要确定神经网络在训练数据中是否可以得到一个好的结果，如果没有，重新进行三步走，看看哪步需要做出一些修改；如果有好的结果且在测试数据中没有得到好的结果，那么就可以判断为过拟合。
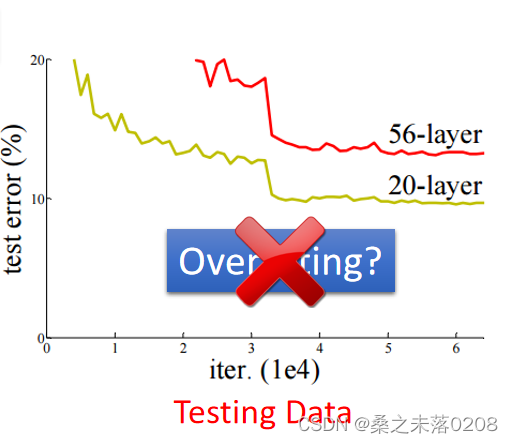
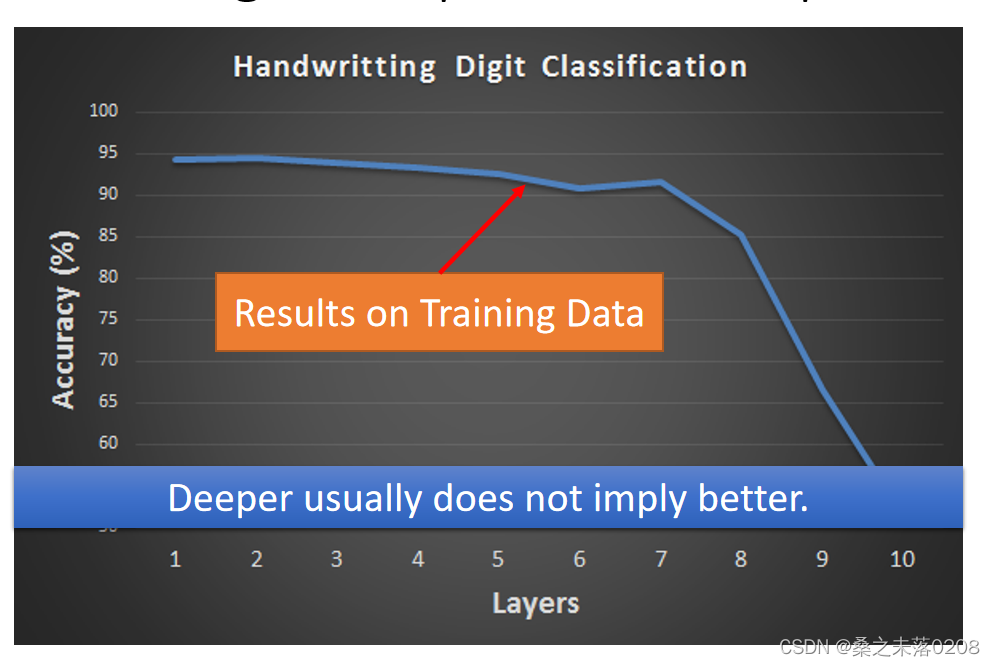
?当看到下面这个图，56层的比20层的测试误差更大，就会判定应该是参数过多，出现过拟合。那么事实上真的是这样吗？这个时候我们需要查看训练数据上两者的情况做出正确的判断。
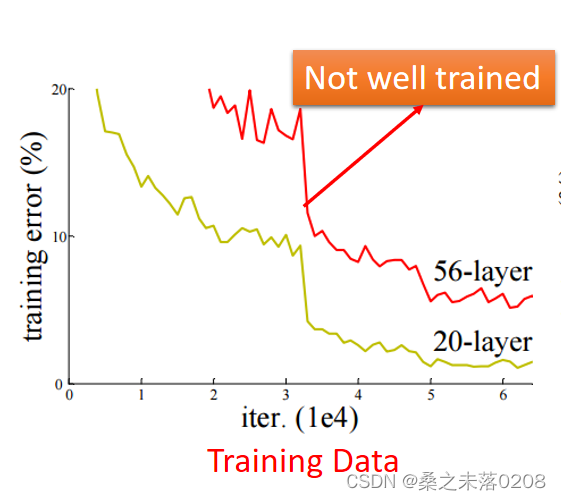
我们从训练数据可以看到56层的神经网络是没有训练好。
new activation function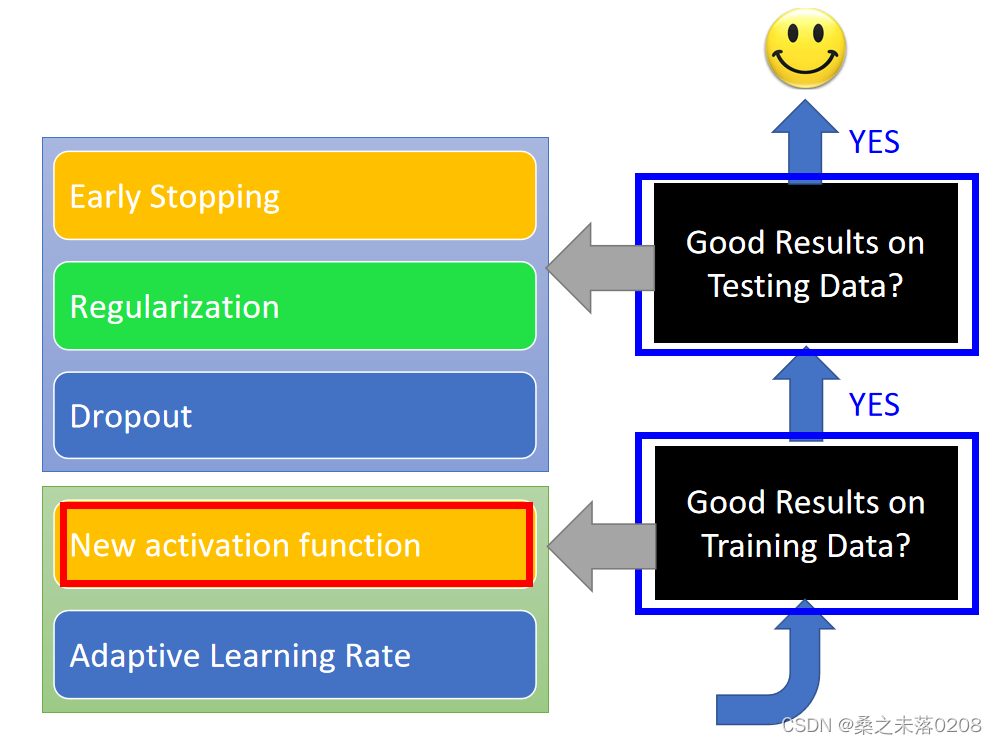
?事实上，层数越多并非意味着最好。
?特征：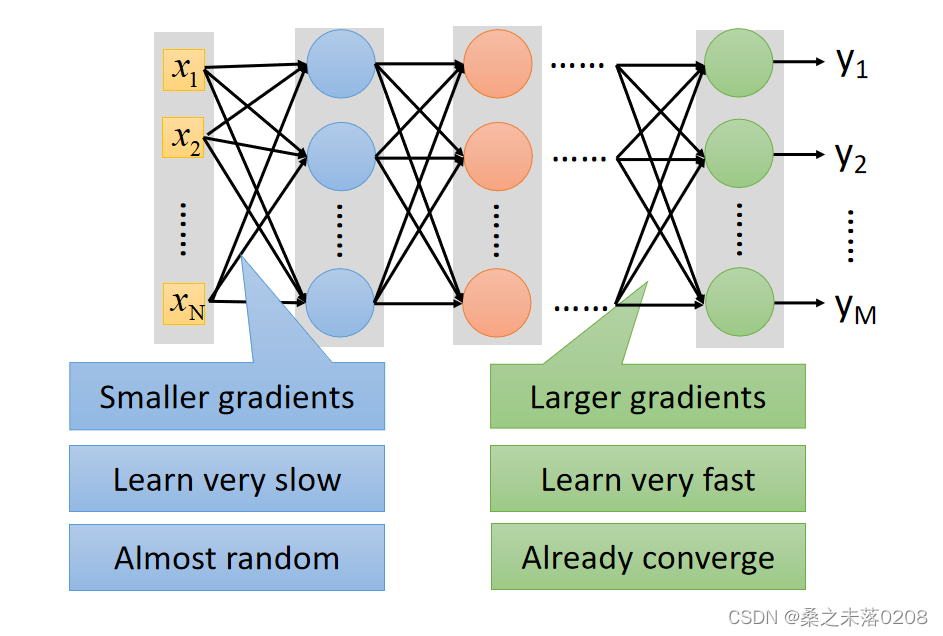
?为了使得输出层的损失值变小，在输入层处添加一个
。但是对梯度的影响是越来越小，输出层损失值就不会变很小，例如sigmod函数。
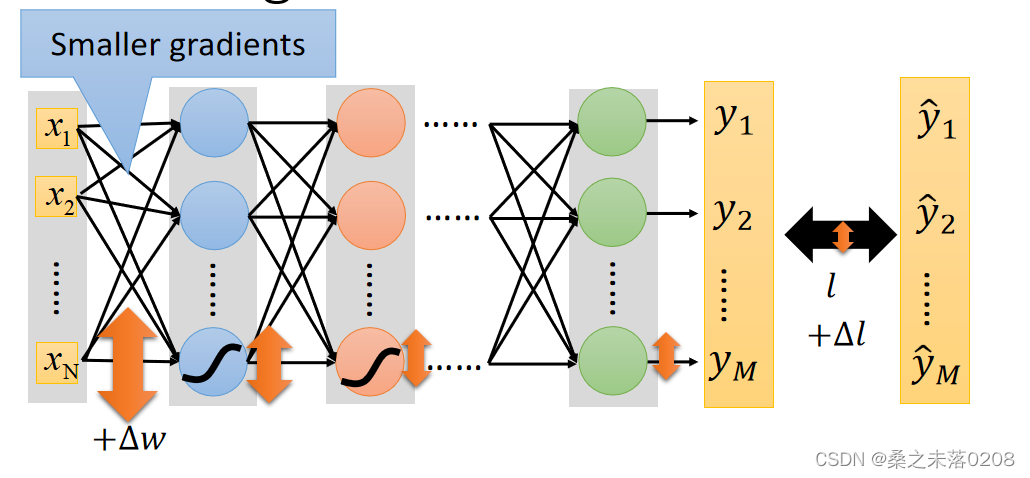
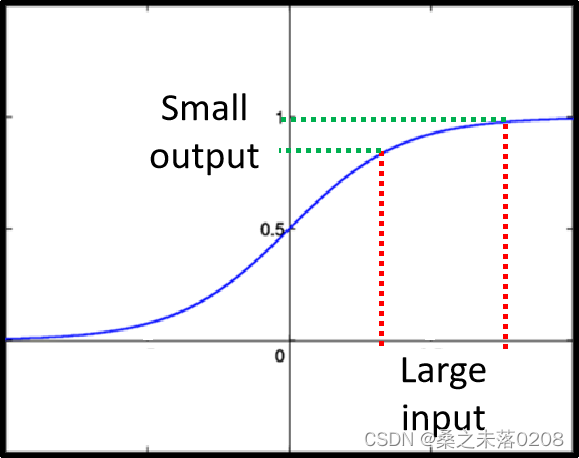
?sigmod函数：很大变化的输入会产生很小变化的输出，如下：
?
?那么，如何解决这个问题呢？
我们采用的方法是：Rectified Linear Unit（ReLU）
假设a——输出，z——输入，两者之间的关系如下所示：
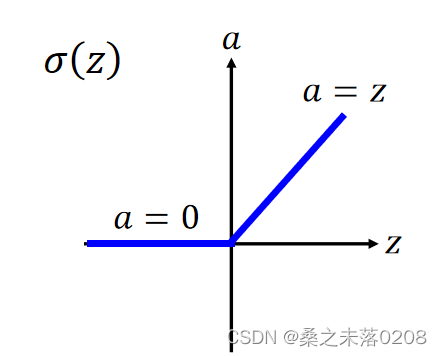
?选择这样的关系有以下几个理由：
（1）计算快
（2）生物上的理由
（3）无穷多的sigmod函数叠加的结果
（4）最重要的是：可以解决梯度问题
ReLU进阶版：Leaky ReLU、Parametric ReLU、Maxout
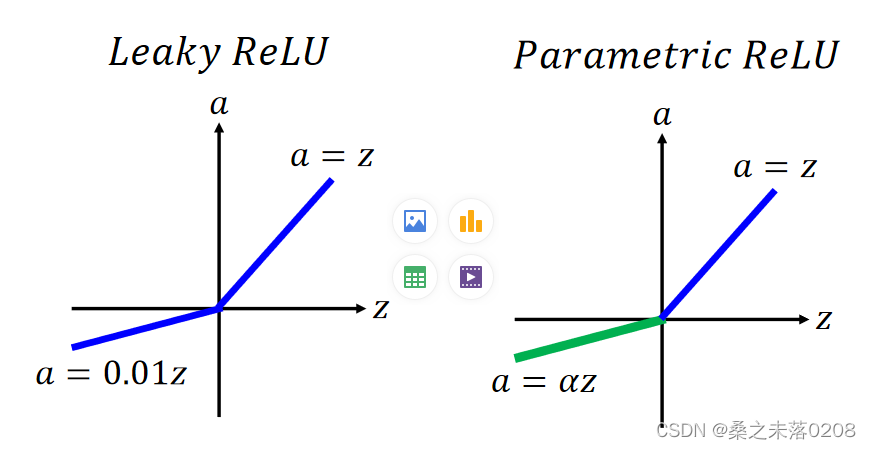
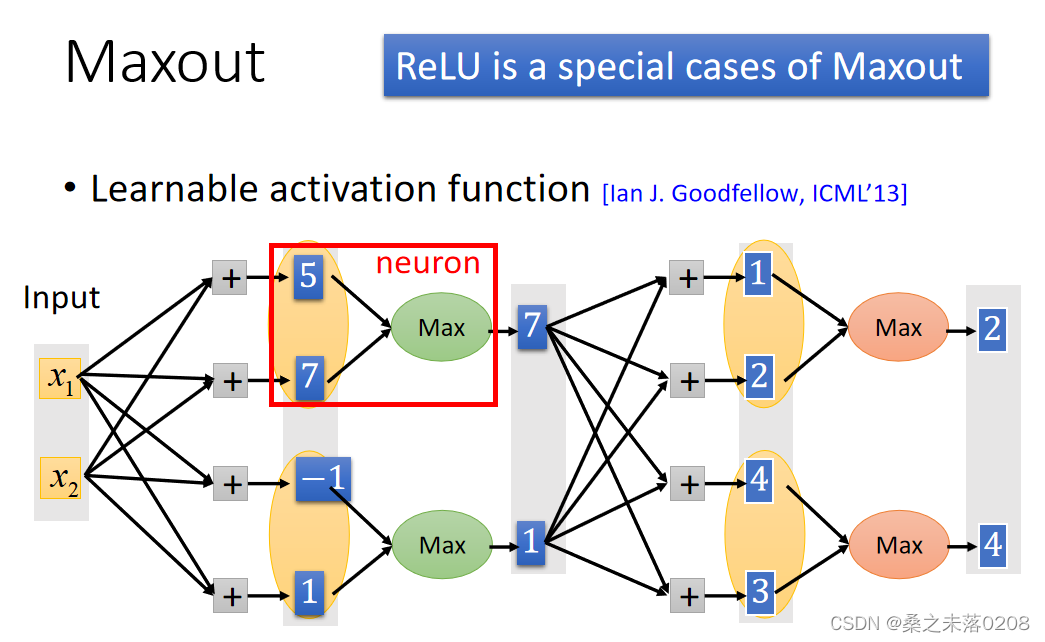?PS:Maxout可以得到ReLU，如下图：
?
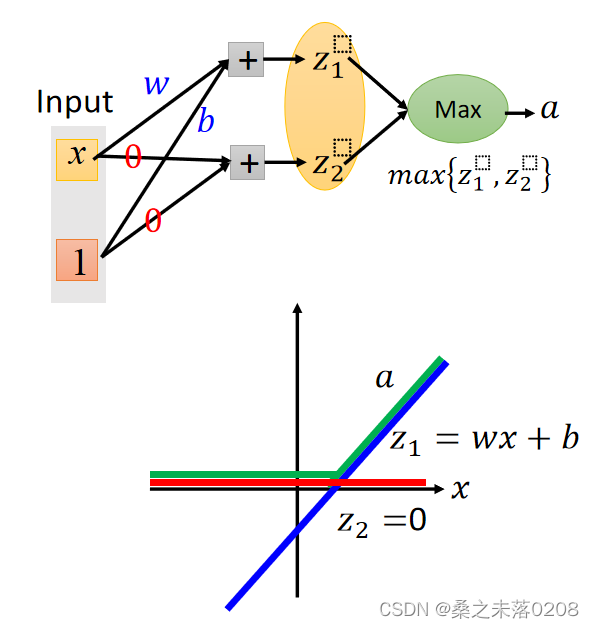
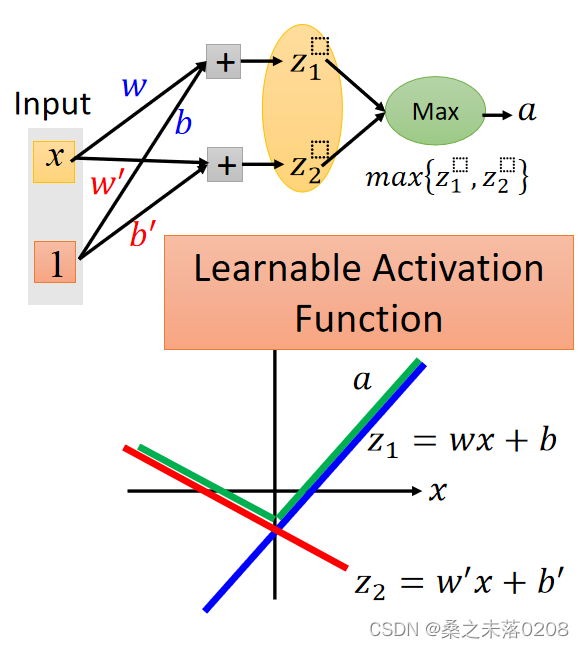
Learnable activation function的特征：?
（1）maxout中的激活函数可以是任意分段线性凸函数；
（2）多少块取决于一组中有多少个元素。
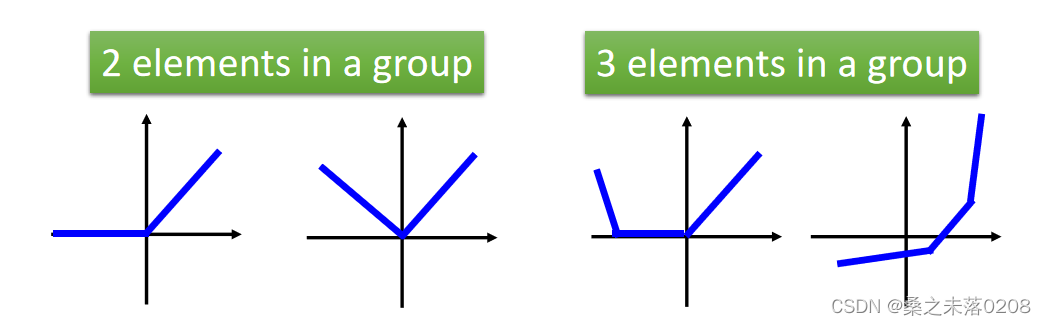
?那么，给定训练数据的输入值x，如何得到最大的输出值呢？
?Maxout中，我们在每一步选择最大值（即，红色框框部分），这样我们就可以得到一个细而线性的网络，如下图所示。然后对其训练。
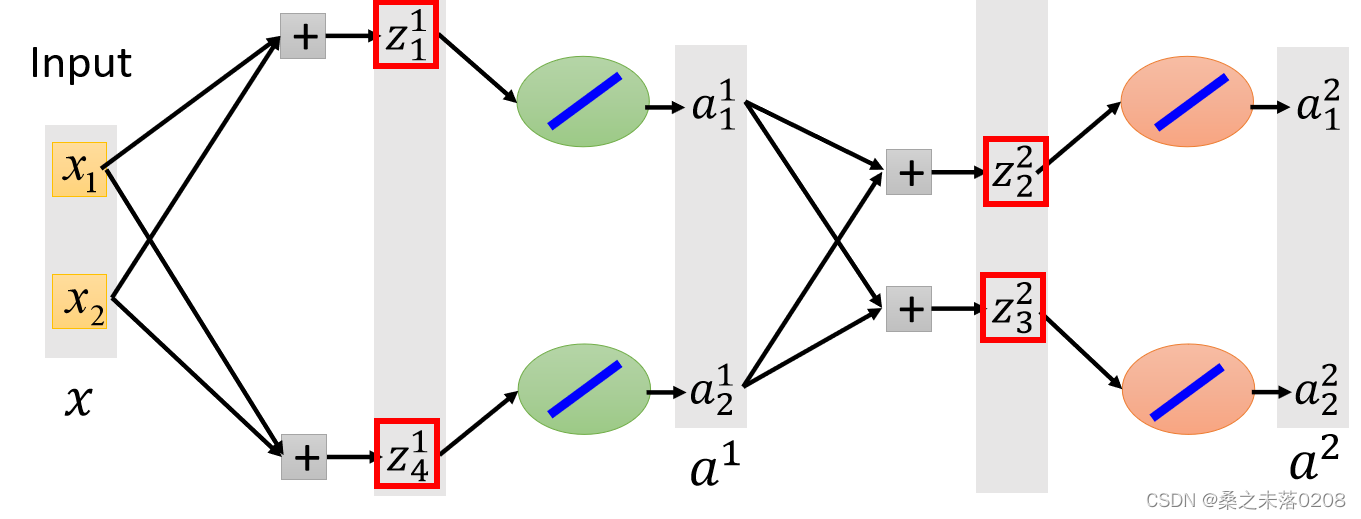
?Adaptive Learning Rate
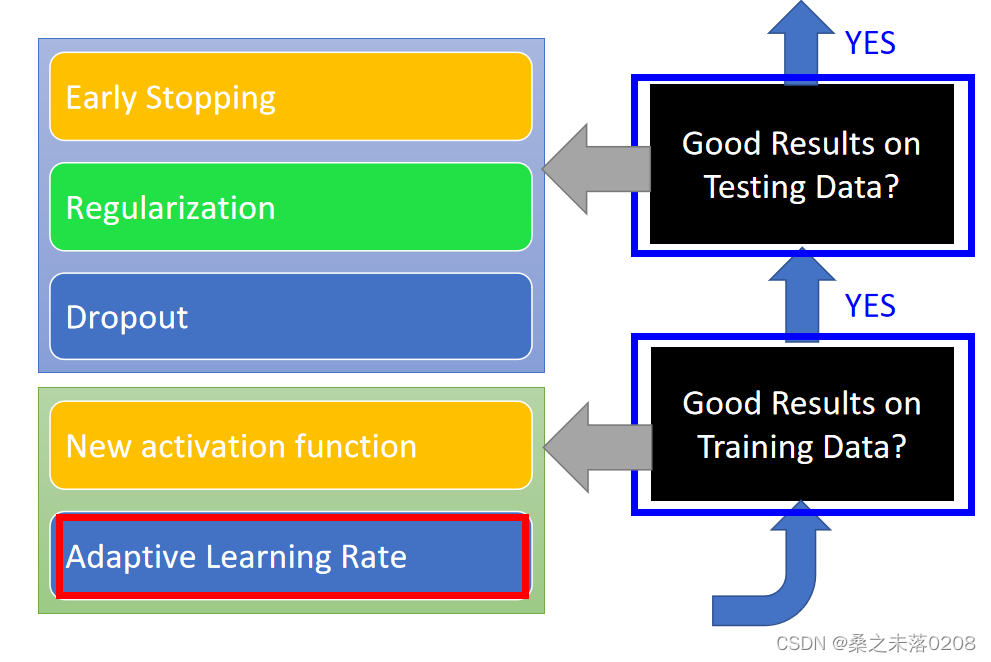
Adagrad：
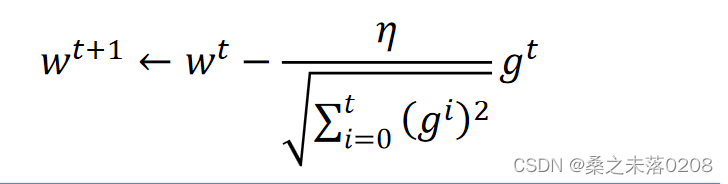
RMSProp：其中可以自行调整
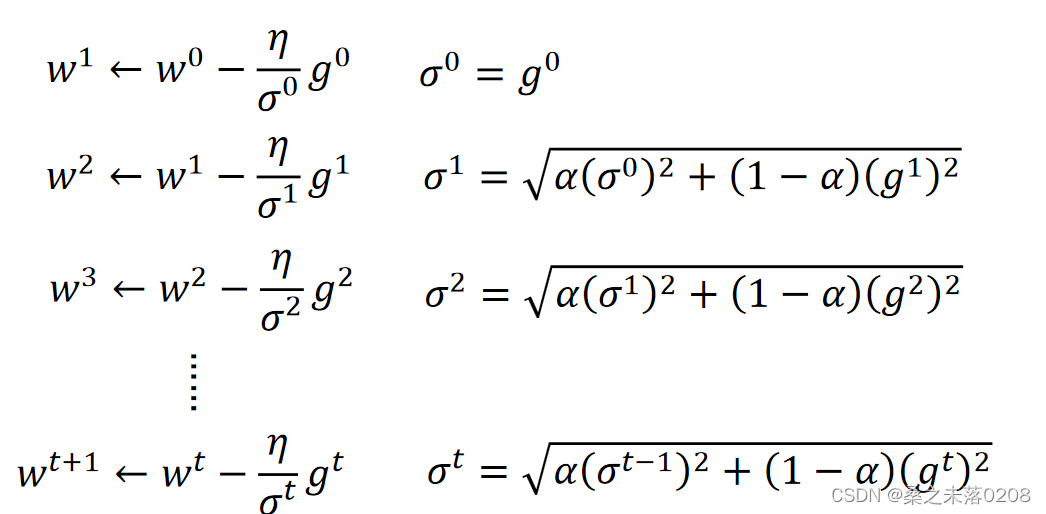
local minima问题
?解决办法——Momentum，简单来说，在真实世界中，小球会因为惯性而一直向前，从而度过了局部最低点，从而解决了Momentum。具体见https://blog.csdn.net/qwertyuiop0208/article/details/126348658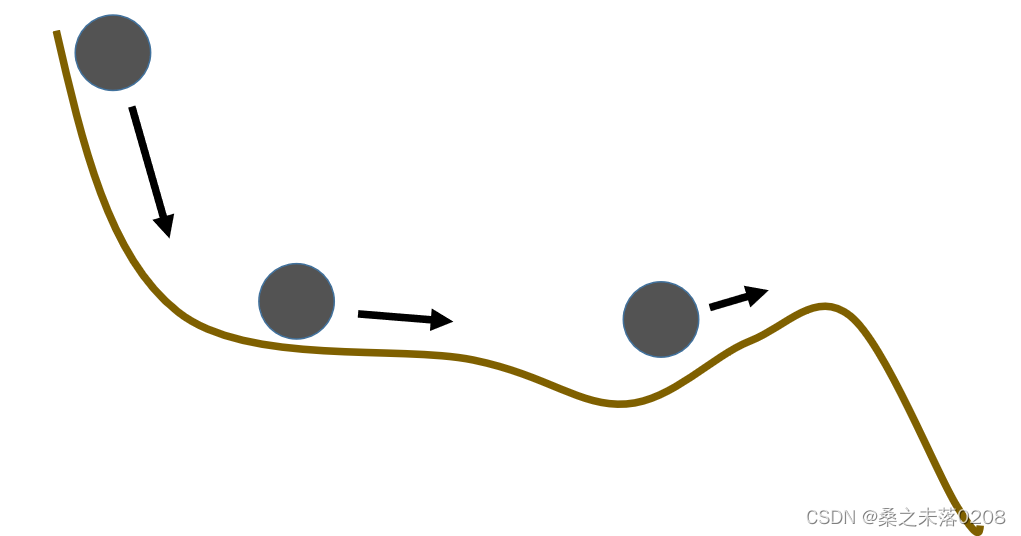
Early Stopping
?Regularization
要最小化的新损失函数，就要找一组不仅使原始损失（例如：最小化平方误差、交叉熵）最小而且接近于零的权重。
权重是在慢慢下降的。
Dropout
??每次在更新参数之前,每个神经元都有p%的丢失率，当某个神经元丢失，那么就会失去作用。
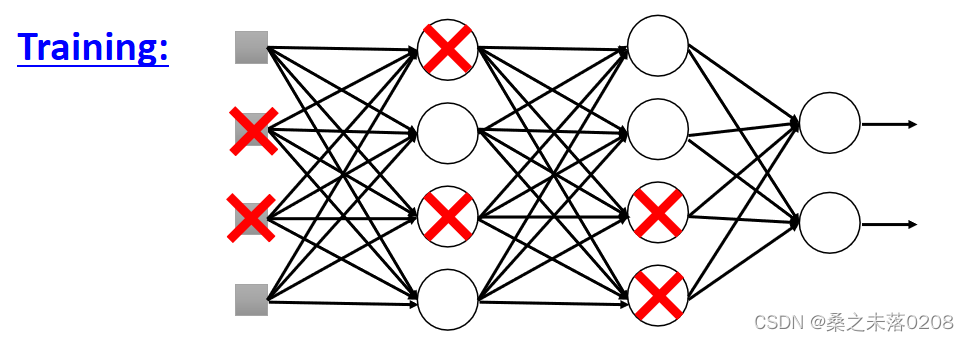
?从而导致网络的结构发生了变化（变得细长），所以要使用新网络进行训练。对于每一个小批，我们对丢失的神经元进行重新取样。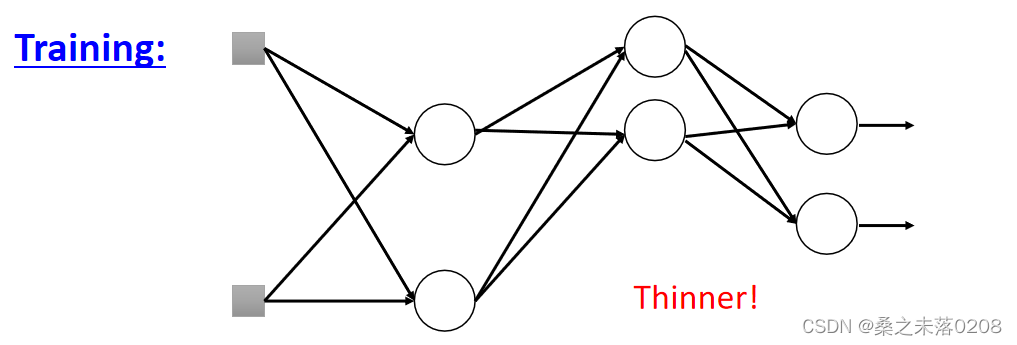
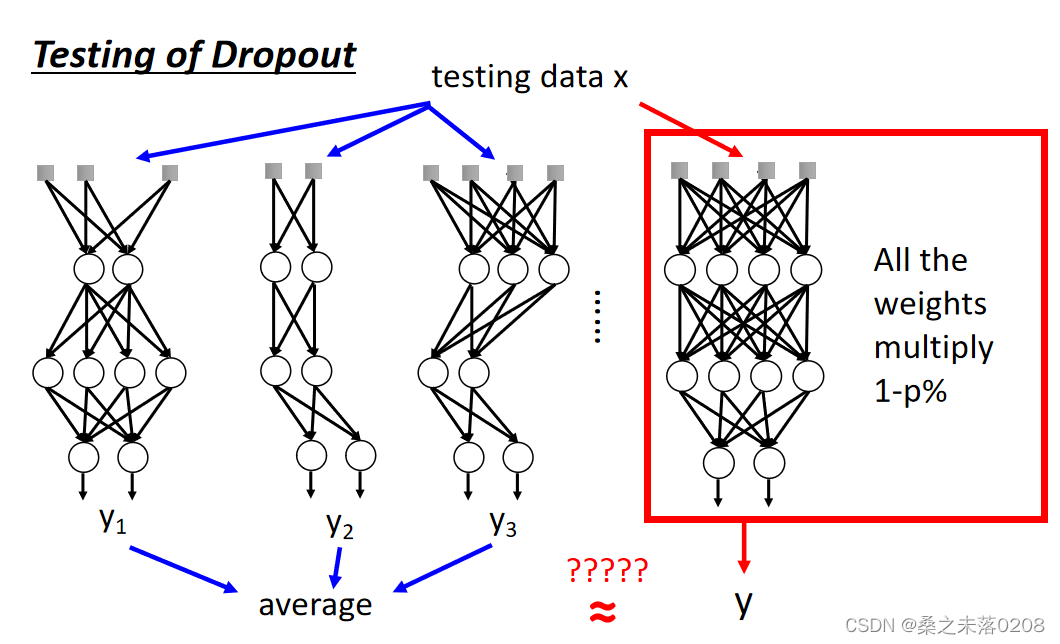
?而在测试的时候，注意两件事情：
（1）不做dropout操作。
（2）如果训练时的丢失率是p%，那么所有的权重需要乘以1-p%。例如丢失率为50%，如果通过训练使权重w=1，则设置w=0.5进行测试。
测试时不做dropout操作的直觉原因：
（1）训练时脚上绑了重物，而测试时重物被拿掉，自然就会变得很强。
（2）?当团队合作时，如果每个人都期望合作伙伴会做工作，最终什么也做不成。然而，如果你知道你的伙伴会dropout，你会做得更好。所以在测试时不做dropout操作，所以最终获得了好的结果。
测试时权重要乘以(1-p)%(丢失率)的直觉原因：
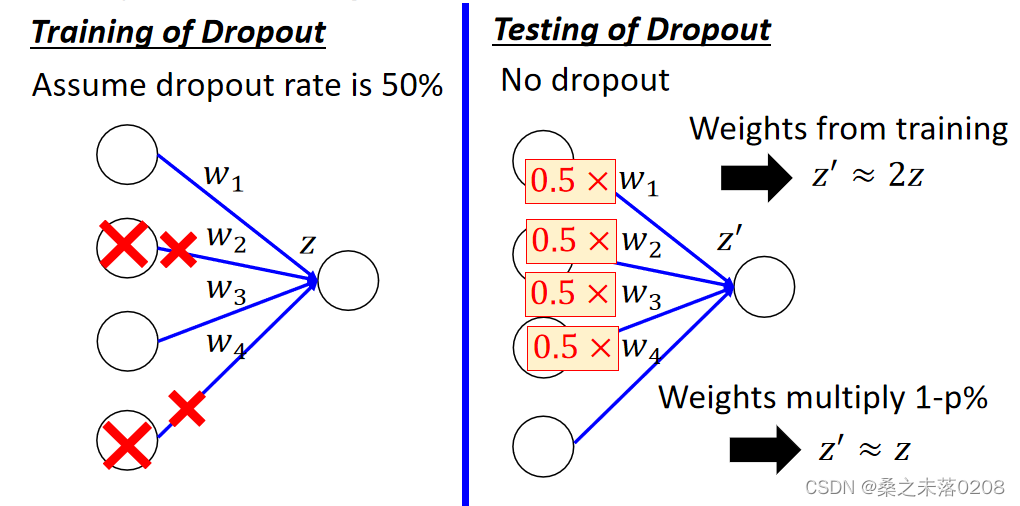
Dropout is a kind of ensemble：
ensemble是训练一堆不同结构的网络
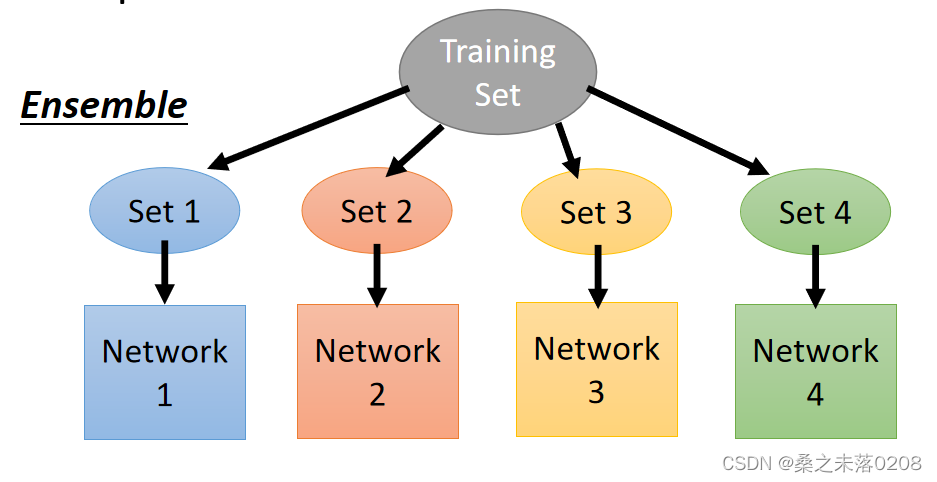
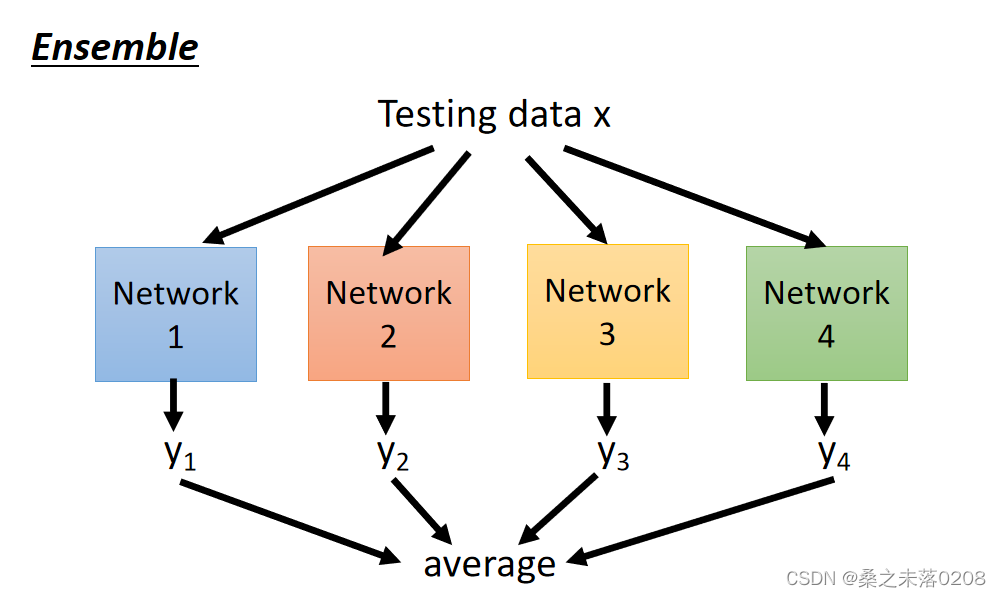
?在dropout时就会产生很多种网络。不同网络的参数有可能是共用的。
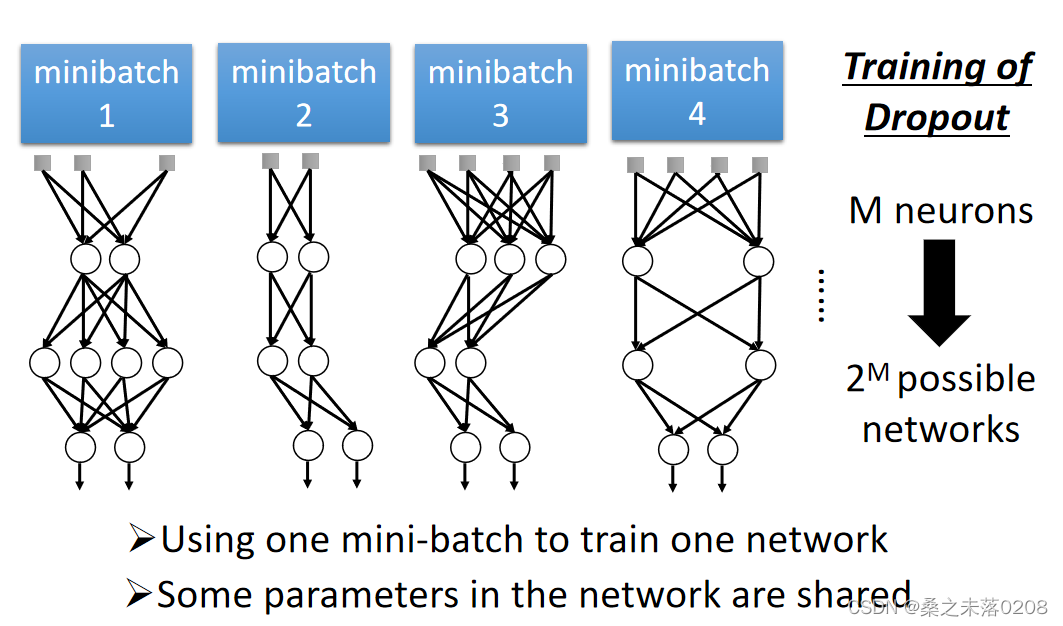
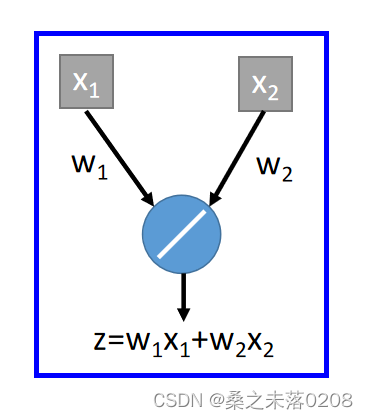
?举例：输入值为，输出值为
。
?ensemble:输入值有可能被dropout，有可能不被dropout，所以就会产生四种情况。
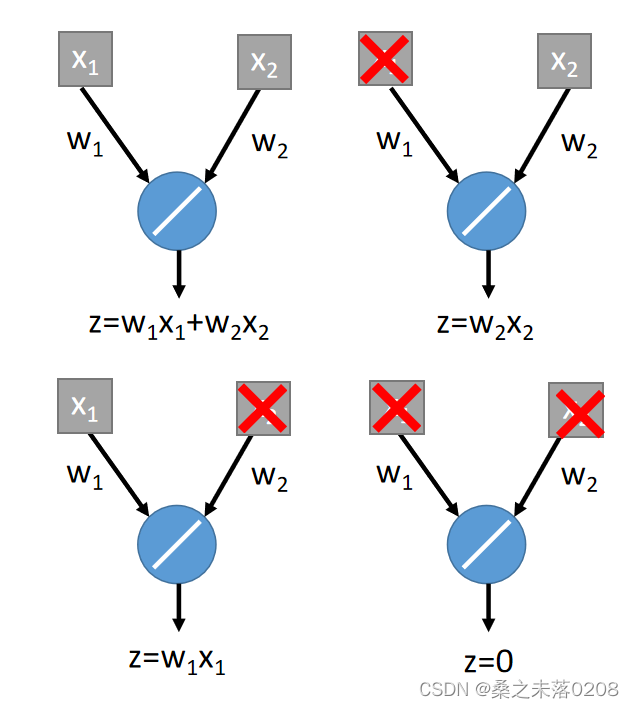
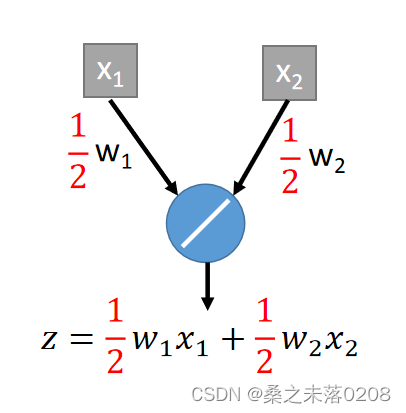
将这四种情况平均一下得到：
如果我们改变权重，不做dropout，那么也能得到平均后的结果，如下：?
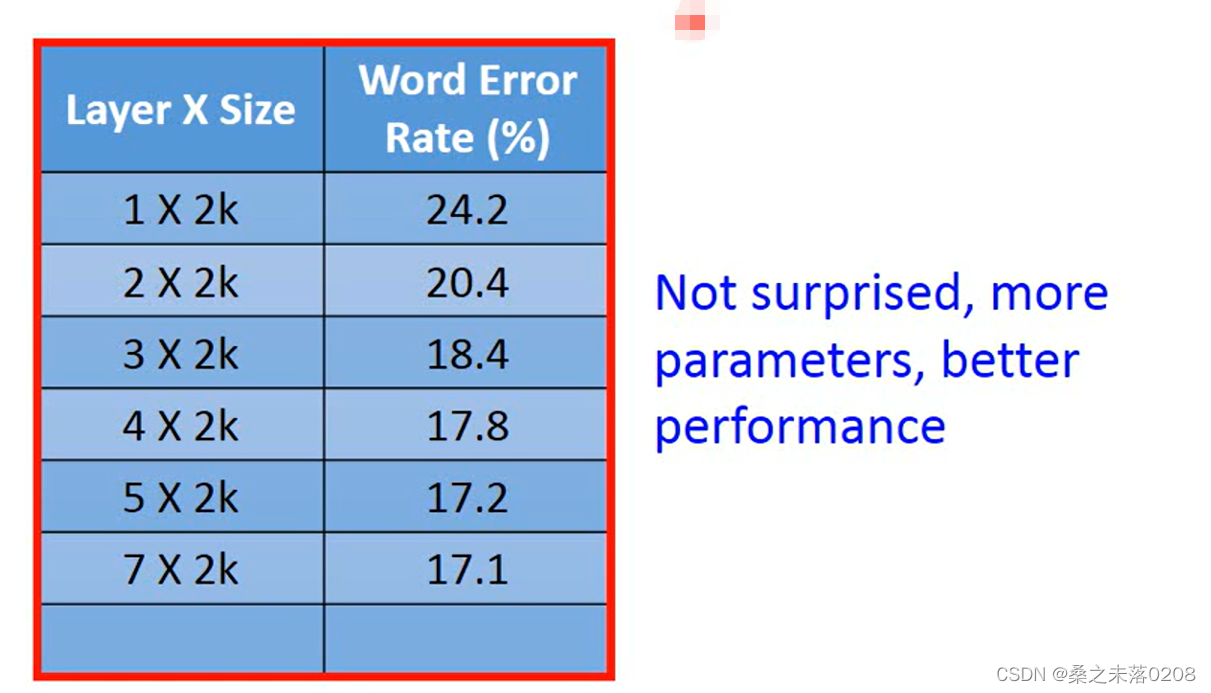
Why deep Learning?
我们可以看到，参数越多，错误率就越低，网络就越好。
?那么，同等参数下，是又胖又短的网络（shallow model）还是又瘦又长的网络（deep model）好呢？
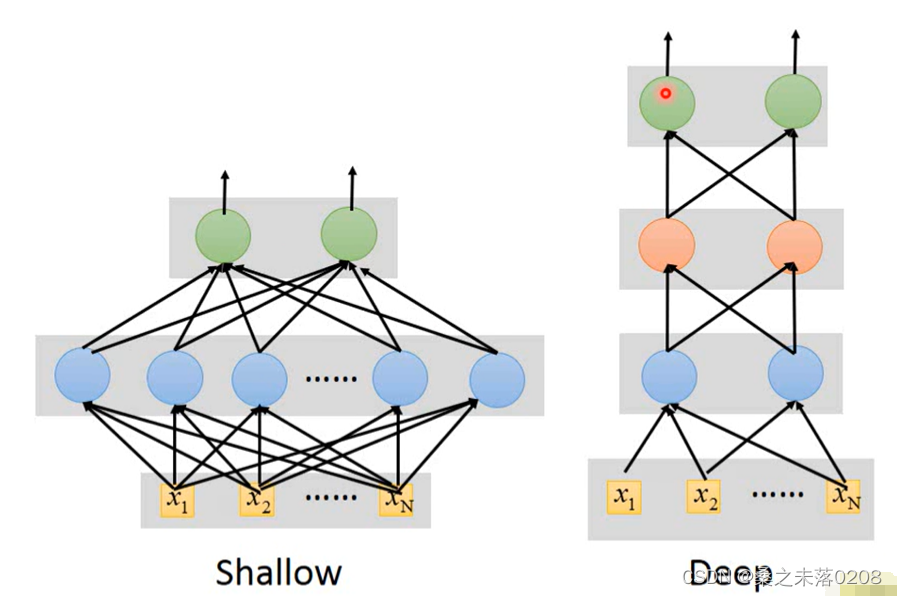
?我们可以看到，层数少，参数多的反而没有那么好，这是为什么呢？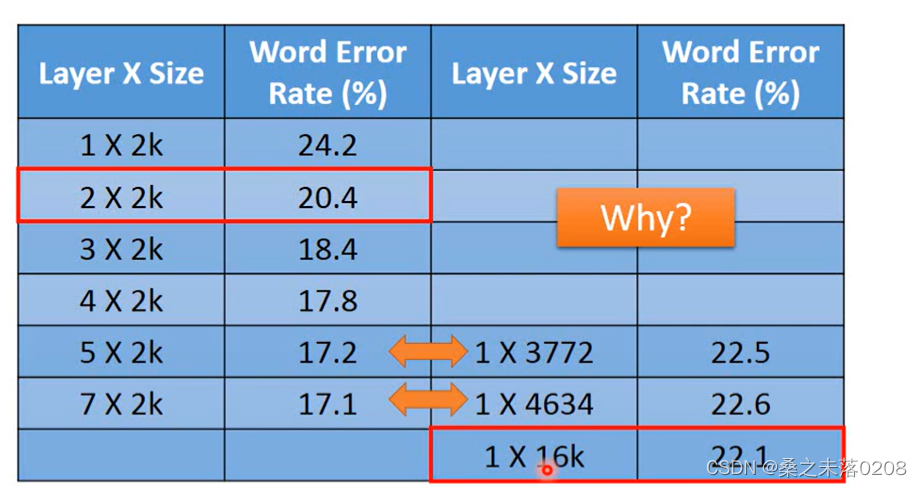
?modularization（模块化）
?事实上，当我们写写程序时，我们并不会将所有的部分作为主要程序，而是将其模块化，如下：
举个例子：对一个人的判断分为长发女、短发女、长发男、短发男四种。显然，长发男的数据相对其他三种肯定是比较少的，所以将有很少的数据可以拿去训练，那么这个时候该怎么做的？
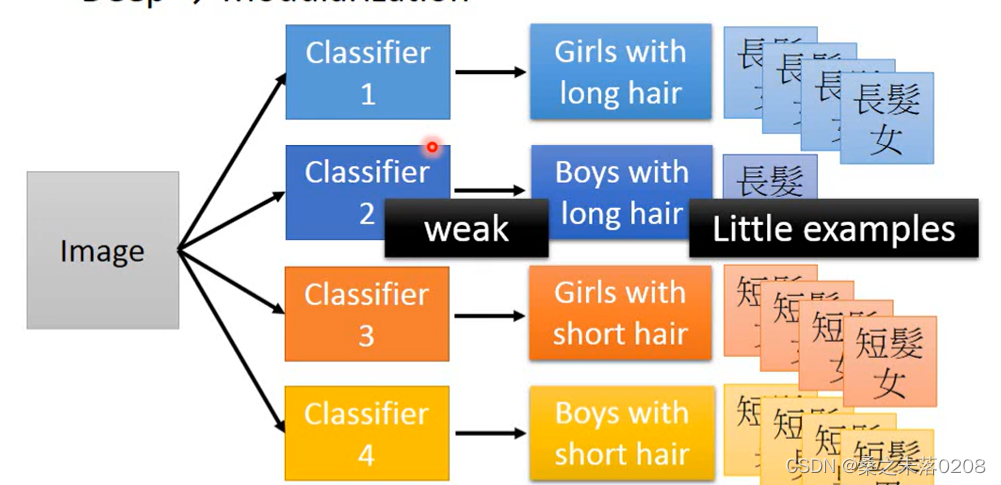
modularization是先进行一个基础的分类：男生or女生、长发or短发。
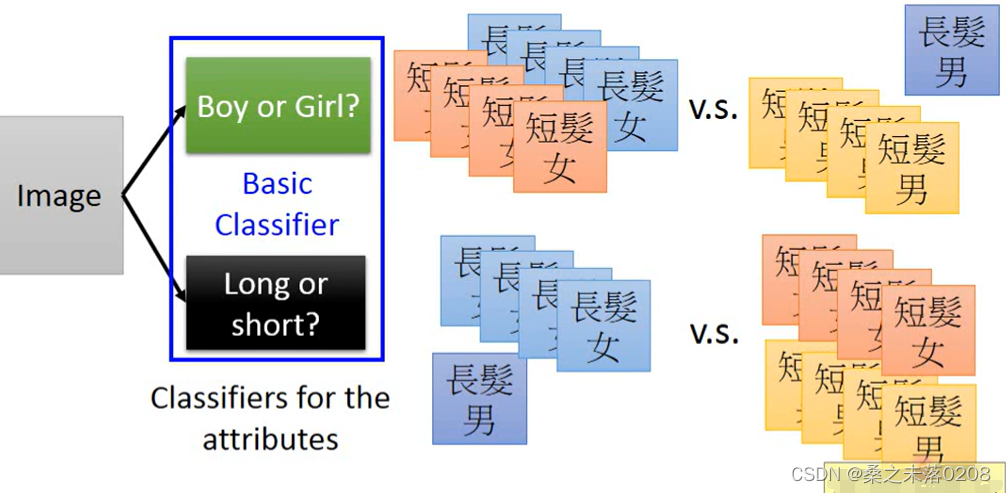
通过基础分类，就可以训练较少的数据，得到较好的结果。?
?模块化和深度学习关系如下图，模块化是从数据中自动学习的
?Universality theorem
只要有够多的参数，那么就可以代表任何的函数，但是当我们只用一个到一个隐藏层是没有效率的，只有深层结构才更有效。
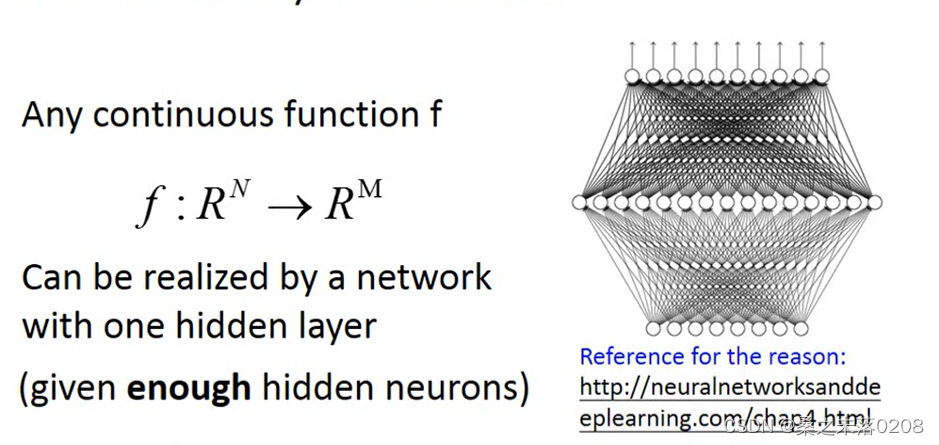
deep learning 优点
深度学习可以解决复杂的问题，例如很相似的输入可能有不同的输出；很不同的输入可能有相同的输出。
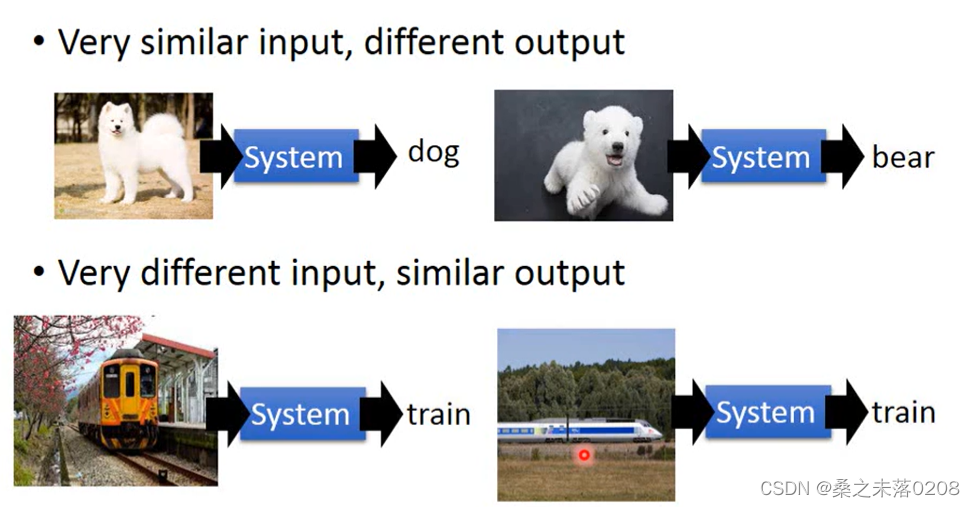
?举例：图像上，可以很清晰得将相同的类归在一起，不同的类分开。
?