ABSTRACT
Agnostophobia, the fear of the unknown, can be experienced by deep learning engineers while applying their networks to real-world applications. Unfortunately, network behavior is not well defined for inputs far from a networks training set. In an uncontrolled environment, networks face many instances that are not of interest to them and have to be rejected in order to avoid a false positive. This problem has previously been tackled by researchers by either a) thresholding softmax, which by construction cannot return none of the known classes, or b) using an additional background or garbage class. In this paper, we show that both of these approaches help, but are generally insufficient when previously unseen classes are encountered. We also introduce a new evaluation metric that focuses on comparing the performance of multiple approaches in scenarios where such unseen classes or unknowns are encountered. Our major contributions are simple yet effective Entropic Open-Set and Objectosphere losses that train networks using negative samples from some classes. These novel losses are designed to maximize entropy for unknown inputs while increasing separation in deep feature space by modifying magnitudes of known and unknown samples. Experiments on networks trained to classify classes from MNIST and CIFAR-10 show that our novel loss functions are significantly better at dealing with unknown inputs from datasets such as Devanagari, NotMNIST, CIFAR-100, and SVHN.
图像分类任务,作为计算机视觉中最基础的任务,看似简单,却在实际应用中常面临一些不足。鲁棒性(Robustness)、开集问题(Open-set)、类别不均衡(Class imbalance) 这些都是在学术数据集上很少考虑,而实际中常见且直接影响算法效果的问题。这篇文章讨论的是开集问题。简言之,开集问题是在测试时如何针对训练集不包含的类别数据进行预测/分类。(题外话,人脸识别就是典型开集识别问题,训练集中 ID 和应用场景中 ID 往往有较大差异,采用度量学习方法)不考虑开集问题,在实际中会造成大量 false positive,影响使用体感。
文章中以手写数字识别为例(0-9,10分类问题),将 Devanagari 数据集作为开集数据。采用 LeNet++ 作为backbone,将图片映射到 2 维特征空间,进而预测 0-9 类别。
符号表
| 符号 | 含义 |
|---|---|
| Y | 所有类别空间 |
| C | 已知类别,known classes (1…C) |
| U | 未知类别,unknown classes |
| B | 未知类别子集1,background, garbage, or known unknown classes. |
| A | 未知类别子集2,unknown unknown classes |
| D | 测试数据集 |
| D’ | 训练数据集 |
相关工作
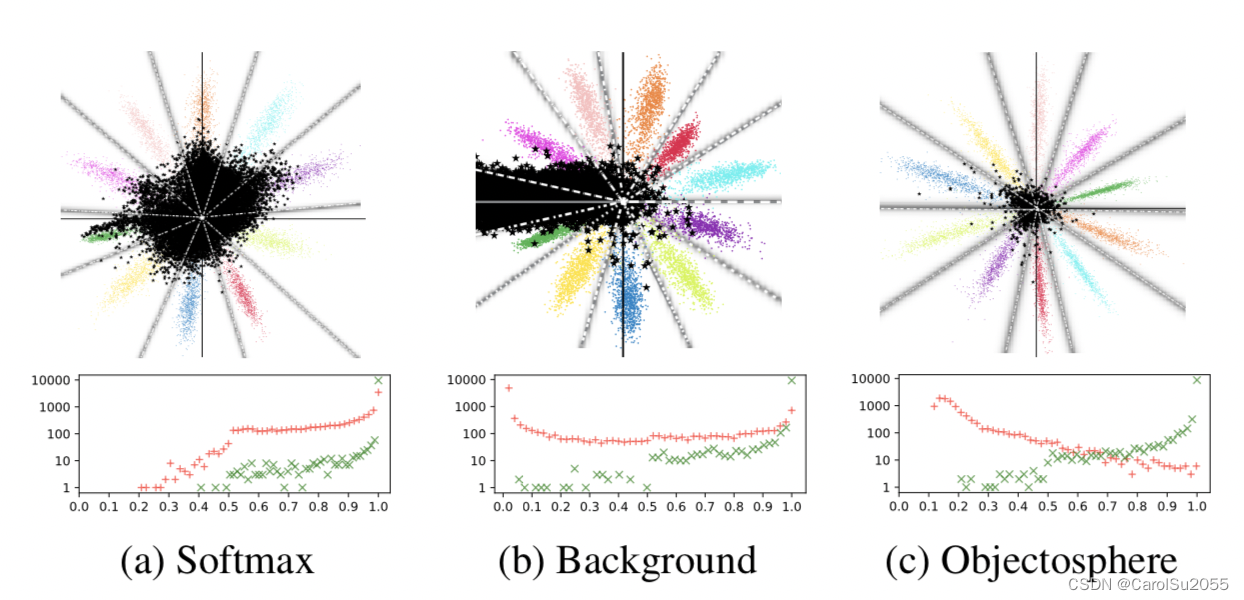
传统多分类问题,采用 softmax 层对 logit 计算概率分布,选择概率值最大 (argmax) 的类别作为预测类型。下图中,彩色散点表示 MNIST 数据样本分布情况,属于C - known classes;黑色散点表示 Devanagari 数据样本分布情况,属于U - unknown classes。图 a 可见,采用传统 softmax 方法,已知类别/未知类别有大量重叠区域;从下方的直方图也能看出,存在较多未知类别样本在某一类别上的预测概率较高,形成 false positive。即便选择某个概率阈值,也很难将 FP 和 TP 区分开。
现有文献中的解决方法包括四种:
1. Thresholding Softmax Scores
训练数据不变,网络结构不变,改进 softmax 函数,在分母中增加一个指数项 e^alpha。促使 logit 值大于 alpha。
2. Uncertainty Estimation
采用 model ensemble 度量不确定性。构造对抗样本训练 M 个模型,并计算 M 个模型预测的方差衡量不确定性。
3. Open-Set Approach OpenMax
以各已知类样本拟合得到的Weibull模型 (meta-recognition system) 判断闭集分类模型 (recognition system) 分类失败的概率,并以分类失败的概率矫正已知类得分+计算未知类得分。
Ref: https://blog.csdn.net/weixin_42188082/article/details/122009841
4. Background Class
网络结构和训练集中增加一个未知类别,将不属于已知类别的样本都预测为未知类别。
本文提出的方案
针对开集问题,设计两个损失函数,不改变模型结构,但训练集中加入 unknown class 样本,属于B。
1. entropic open-set loss
最大化模型 softmax layer 输出的熵值。
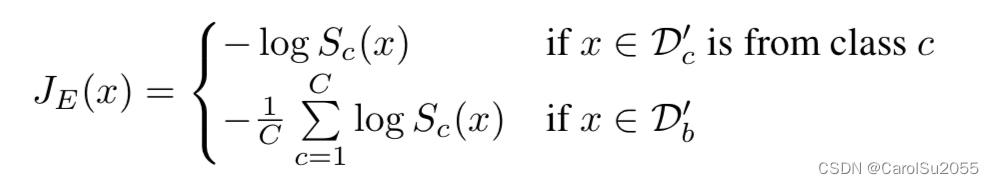
- case1: x 属于已知类别,和交叉熵函数一致
- case2: x 属于未知类别子集1,最大化预测概率分布的熵值
2. objectosphere loss
在 entropic open-set loss 基础上,约束特征向量的模长。F(x) 是 logit layer 的输入。
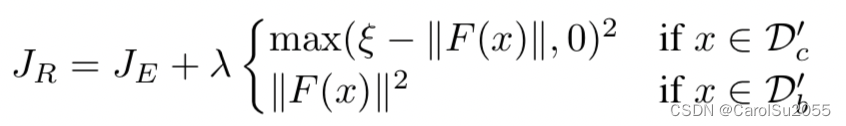
- case1: x 属于已知类别,约束特征模长值大于阈值。
- case2: x 属于位置类别,约束特征模长值趋近于0。
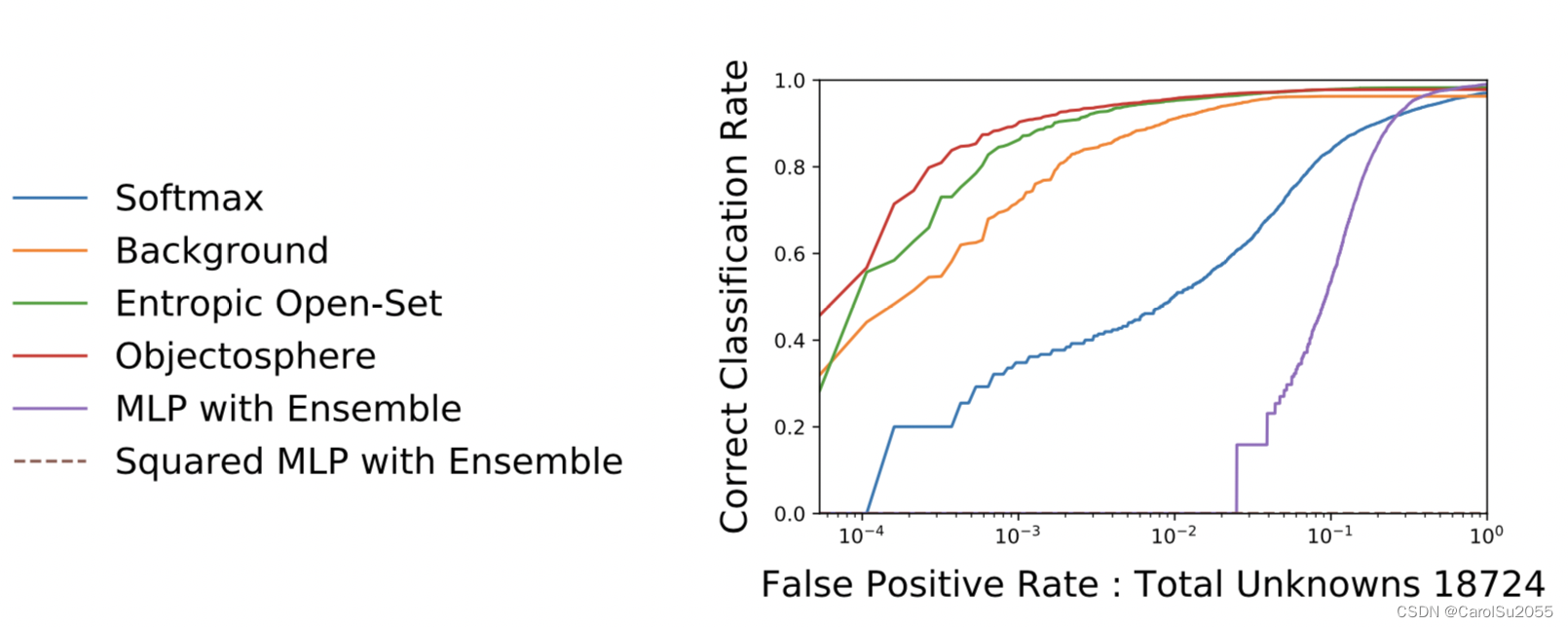
3. 度量指标 - Openset classification rate curve
theta: 概率阈值
FPR: False Positive Rate
CCR: Correct Classification Rate