卷积神经网络
1.image classification
我们首先要知道图片是怎么做分类这个工作的,基本的流程是:输入图片到一个模型中,这个模型输出一个很长的向量,并用此向量来进行分类。这个向量是怎么进行分类呢?首先我们的
y
^
\hat{y}
y^?也就是真值向量,是类似于one-hot的一种形式,如果代表的是狗,那就是狗那一级为1,其他全部为0。而我们输出的向量则是
y
′
y'
y′,里面的参数与
y
^
\hat{y}
y^?进行cross entropy来进行训练。当然如果你希望辨识1000种2000种类别,那么向量就要设置对应的1000,2000行即可。
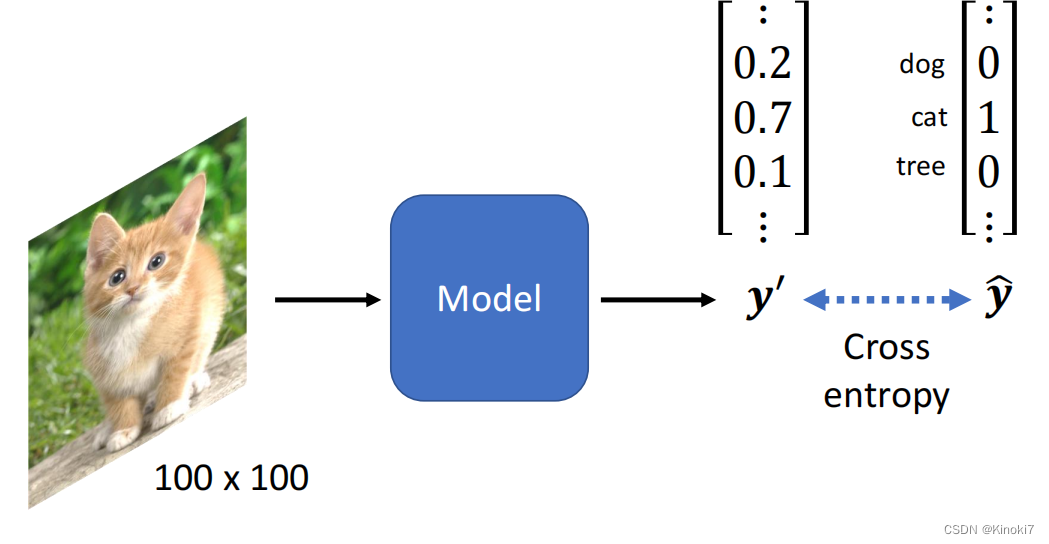
这里涉及到另外一个问题,就是图片如何来当作输入。其实我们的图片是一个三维的tensor,三维分别是:宽、高和channel的数目。一般彩色图片的channel数目是3,代表的是RGB,所以上图就是一个100×100×3的图片,我们可以将其进行拉伸,将其变为一个向量,向量即为100×100×3行,将其当作输入即可。
observation1 and simplification1
假如我们跟之前一样使用Fully Connected Network的话,那我们100×100×3的向量进入输入,假如有一hidden layer有1000个Neuron,那我们训练时就需要3×10^7个参数,这样的话我们虽然增加了模型的弹性和能力,同时也有了overfitting的风险,所以我们想到对图像进行处理时,依靠图像的特性是否可以减少模型弹性而得到更好的结果?
所以我们进行了observation1,我们观察到,比如说我们在进行鸟的辨别的时候,我们每一个Neuron其实是在判断鸟的一个特性,比如说鸟嘴、眼睛等,但我们其实并不需要看全部的图像,而是只需要看它的一个小范围里面的图像,所以这些neuron不需要以全部图像当作输入,而只需要一小部分。
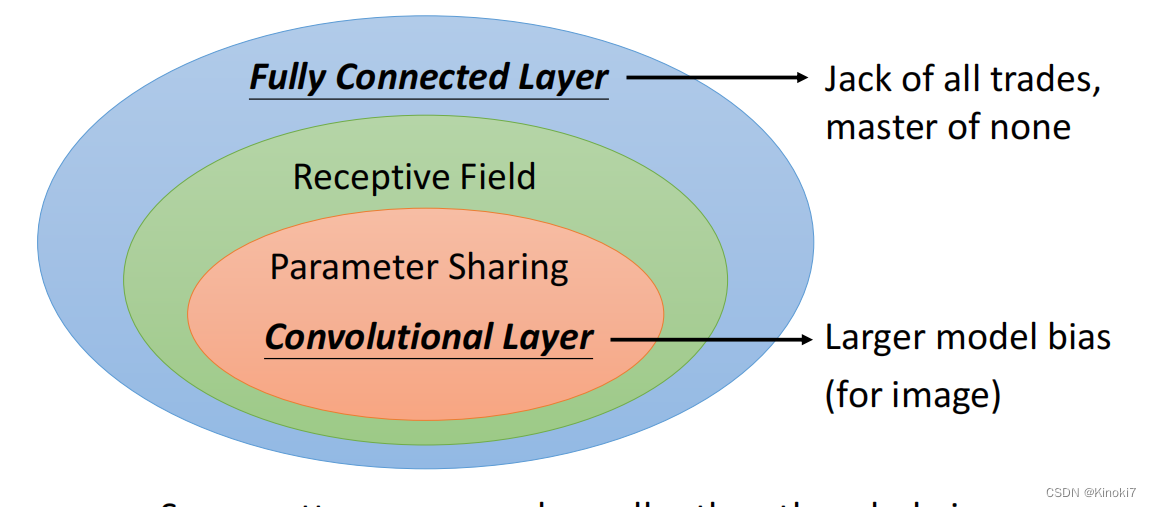
以此为依据我们进行simplification1,即将图像分割成一个一个的Receptive field,每个receptive field都有neuron来守备。这样就达到了看小部分的结果。由此我们又可以引出经典的讲解中kernel size, padding, stride这些概念。
observation2 and simplification2
我们observation1虽然说是只看图像的一部分,但一些特征可能会出现在图像的不同的地方。那我们在训练的时候是否需要在两个地方都需要一个neuron来进行守备呢?
所以我们想到了simplification2,就是进行参数共享。在不同的receptive field的不同neuron上,如果他们都检测到鸟嘴,那么我们可以进行参数共享。从这里我们又可以得到经典的讲解中filter的概念,filter就是一系列的neuron共享的参数。
observation3
当对一个较大图像做subsampling后,图像就缩小了,这就是做了pooling,在实操上一般是convolution与pooling交替使用。使用pooling能使图像变小来减少运算量