【斯坦福大学公开课CS224W——图机器学习】二、图机器学习中的传统方法(2)
文章目录
1. 边预测任务和特征
- 这个任务是基于已存在的边来预测新的边
- 在测试阶段,节点对(无边连接)会被排名,前k个节点对来作为预测结果
- 关键是对每一个节点对设计特征
1.1 边预测任务
两种边预测任务设计:
(1)边随机丢失:将图中的随机的一些边移除,然后预测他们
(2)Links over time:

1.2 边层面的特征
- 基于距离的特征
- 局部邻域重叠
- 全局邻域重叠
1.2.1 基于距离的特征
两个节点之间的最短路径距离,然而,这并没有捕捉到领域重叠的程度
1.2.2 局部邻域重叠
捕获两个节点 v1和 v2之间共享的相邻节点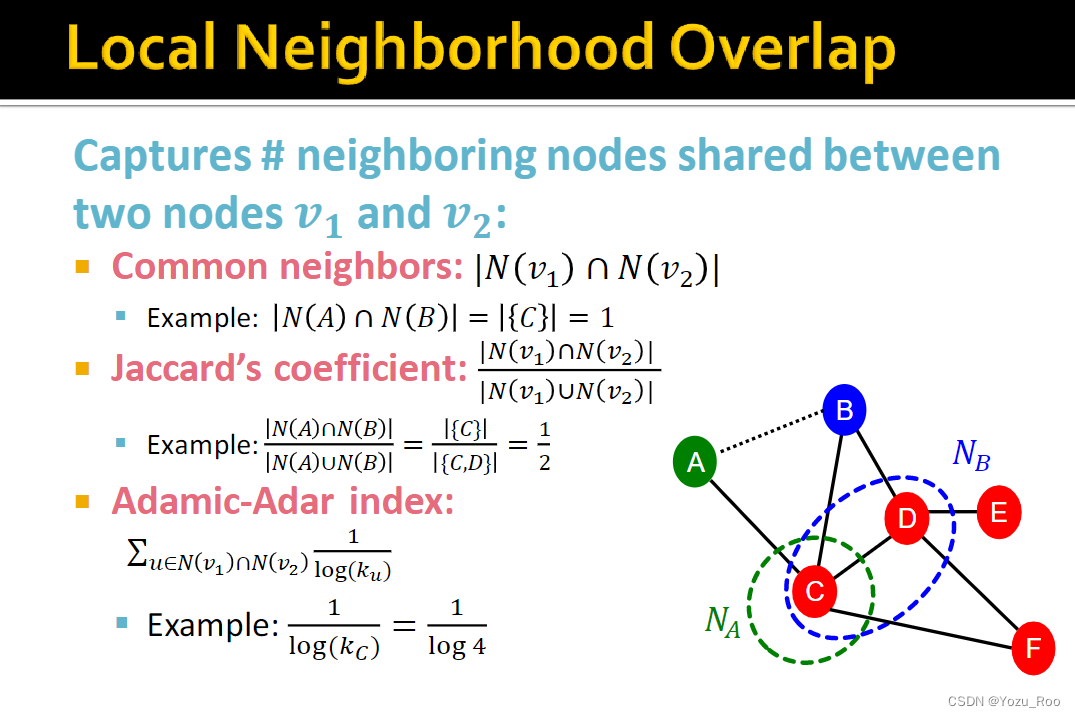
1.2.3 全局邻域重叠
局部邻域特征的限制:如果两个节点没有任何共同的邻居,度量值总是零。但是,这两个节点在未来仍然可能连接在一起。
全局邻域重叠度量方法就解决了这个限制,通过考虑整个图的情况。
Katz index:计算给定节点对之间所有长度的步数。
如何计算两个节点之间的行走的步数? 使用图形邻接矩阵的幂!



2.图层面的特征和图的核
2.1 图层面的特征
目标:我们需要能够表征整个图形结构的特征
核方法背景:核方法在传统的图级预测机器学习中得到了广泛的应用。想法: 设计内核而不是特征向量。
2.2 图层面特征
图内核: 度量两个图形之间的相似性:
- Graphlet Kernel
- Weisfeiler-Lehman Kernel
2.2.1 图内核
目标:设计图特征向量
关键思想: 用于图表的文字袋(BoW)
回顾: BoW 只是使用单词计数作为文档的特性(不考虑排序)。图的扩展: 把节点看作单词。

2.2.2 图元特征
关键思想: 计算一个图形中不同的图形的数量。
注意: 此处的图形定义与节点级特性稍有不同。这两个不同点是:
-
这里的图形中的节点不需要连接(允许独立的节点)
-
这里的图形不是有根的。


2.2.3 图元核

限制: 计算图形代价昂贵!通过枚举计算大小为 n 的图的 size-k Graphlet 的值为 nk。这在最坏情况下是不可避免的,因为子图同构检验(判断一个图是否是另一个图的子图)是 NP 难的。如果一个图的节点度是以 d 为界的,则存在一个 O (ndk-1)算法来计算所有大小为 k 的图。我们能否设计一个更有效的图核?
2.2.4 Weisfeiler-Lehman Kernel
目的: 设计一个有效的图形特征描述符 φG
想法: 使用邻域结构来迭代地丰富节点词汇。由于节点度是单跳邻域信息,所以节点度袋的通用版本。
实现这一点的算法: 色彩细化


WL 内核计算效率高?每一步色彩细化的时间复杂度在 # (边)中呈线性,因为它涉及到相邻颜色的聚合。在计算内核值时,只需要跟踪两个图中出现的颜色。因此,# (颜色)最多是节点的总数。计算颜色采用线性时间 w.r.t. # (节点)。总的来说,时间复杂度在 # (边)中是线性的。