论文来源
@InProceedings{Dai_2017_ICCV,
author = {Dai, Jifeng and Qi, Haozhi and Xiong, Yuwen and Li, Yi and Zhang, Guodong and Hu, Han and Wei, Yichen},
title = {Deformable Convolutional Networks},
booktitle = {Proceedings of the IEEE International Conference on Computer Vision (ICCV)},
month = {Oct},
year = {2017}
}
论文聚焦的问题
目标检测、分割等视觉任务中的一个关键挑战在于,目标对象具有很强的不规则性。无论是传统的手工提取特征,还是使用卷积神经网络学习特征,对目标对象几何变换建模的能力主要来自大规模数据或一些先验知识,模型本身并不具有适应性足够强的几何建模能力。
具体地,对于卷积神经网络,卷积单元在固定位置对特征进行采样,池化层以固定的比例进行池化,ROI层将ROI分离为固定的空间单元。然而,固定的位置、固定的比例、固定的空间单元都是人为指定的,并不是从数据中自适应学到的,因此对于不规则特征的提取有着天然的局限。
简言之,传统方法缺乏对不规则对象进行建模的内部机制,论文聚焦于解决这一问题。
主要贡献
本文的主要贡献在于提出了两个新的模块:
● 向传统卷积神经网络中的卷积层中引入可变形机制,提出可变形卷积模块。
● 为常规的感兴趣区域ROI池中的bin位置添加自适应的偏移量,提出可变形ROI模块。
基于这两个新模块以及引入可变形机制的思路,论文搭建了用于目标检测、语义分割的可变性卷积网络。
需要指出的是,这两个模块都是轻量级模块,相较于传统的卷积神经网络,并没有增加很大的时间复杂度。由于这两个模块保留了端对端的学习特性,因此它们可以很容易地通过反向传播进行训练。
提出的新方法
这一新方法的核心在于可变形机制的引入,即使用一个额外的卷积层,为输入的特征图计算偏移量掩码。具体地,可以分为可变形卷积、可变形ROI池化层两个部分。
可变形卷积
相较于传统的卷积运算(即某一邻域内的所有像素点与对应位置的卷积核的值相乘后相加),卷积核内的值对应的位置不再是整数位置,而是在整数位置的基础上,加上x、y两个方向上的偏移量。这一过程可以用如下公式表示。
y
(
p
n
)
=
∑
p
i
w
(
p
i
)
?
x
(
p
n
+
p
i
+
△
p
i
)
y(p_n)=\sum_{p_i}w(p_i) \cdot x(p_n+p_i+\triangle p_i)
y(pn?)=∑pi??w(pi?)?x(pn?+pi?+△pi?)
考虑到偏移后的位置一般是分数,因此使用双线性插值算法计算该位置的像素值。
合理的偏移量通过额外的卷积层学习得到。具体地,我们使用一个卷积层计算与特征图具有相同分辨率的偏移字段,并使用反向传播算法进行优化。
对于每一个像素位置,计算一个偏移量。
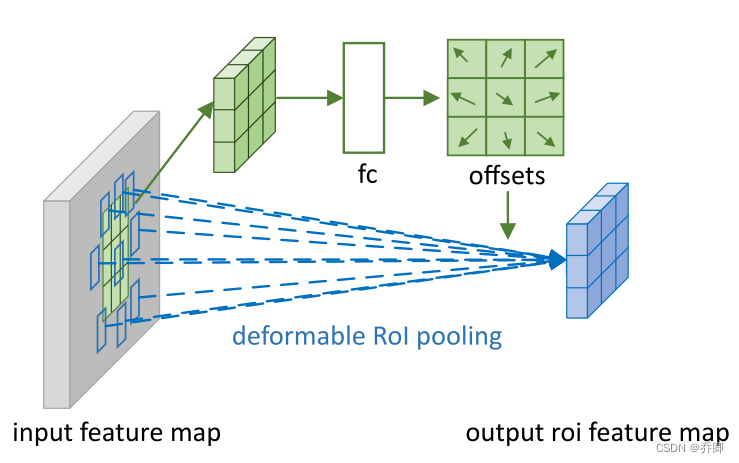
可变形ROI Pooling层
基于区域建议的目标检测方法中(如Fast RCNN)使用到了ROI Pooling层。在传统的ROI池化层中,输入特征图与感兴趣区域,输出固定大小与数目的特征图。在可变形的ROI Pooling层中,通过一个额外的全连接层计算偏移量掩码,将偏移后的位置结合双线性插值算法,应用到ROI最大池化中。这一过程可以用如下公式表示。
y
(
i
,
j
)
=
∑
p
∈
b
i
n
(
i
,
j
)
x
(
p
0
+
p
+
△
p
i
j
)
/
n
i
,
j
y(i,j)=\sum_{p\in bin(i,j)}x(p_0 + p + \triangle p_{ij}) / n_{i,j}
y(i,j)=∑p∈bin(i,j)?x(p0?+p+△pij?)/ni,j?
同样地,偏移量的引入不影响利用反向传播进行优化。
对ROI Polling的理解:ROI就是一个区域,ROI Polling就是将该区域分成若干个(比如33)小区域,在每个区域内Polling(比如平均池化、最大池化),从而将该区域变成指定大小的特征图。对于每个ROI内的小区域计算一个偏移值(比如当有33个小区域时就有3*3个偏移值,一整个区域进行偏移),Polling时取偏移后的小区域,而不是原始的区域。
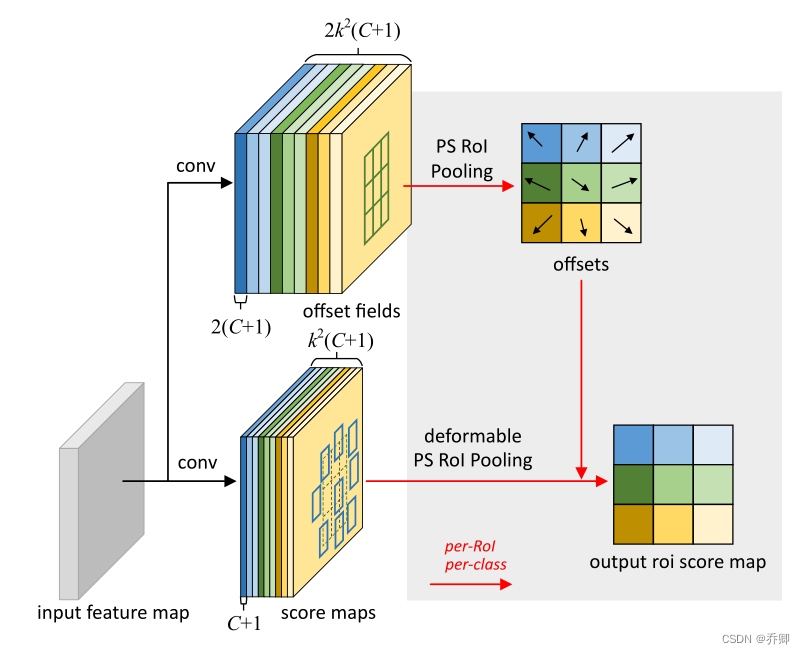
位置敏感的ROI Pooling
对于C个类别,由全卷积生成C+1层score maps、2(C+1)层offset fields,每一层大小为k*k。
在score maps上进行polling,而不是在特征图上进行polling。
由offset fields进一步作PS ROI Polling得到偏移值。
集成了可变形卷积的网络
现有的先进的卷积神经网络的两个部分:
● 深层网络提取特征
● 浅层网络生成结果
与STN的区别:可变形卷积不采用全局参数变换和特征扭曲。相反,它以局部和密集的方式对特征地图进行采样。为了生成新的特征映射,它有一个加权求和步骤,这在STN中是不存在的。
关于有效的感受野:有效感受野只占理论感受野的一小部分,呈高斯分布。虽然理论上的感受野大小随着卷积层数的增加而线性增加,但事实上,有效感受野大小随着卷积层数的平方根线性增加。
我自己对这一方法的理解
在可变形卷积的视角下看,传统卷积、空洞卷积与多尺度卷积可以被认为是可变形卷积在取一定的偏移量时的特例。可变性卷积网络相较于传统的卷积网络,多了一个用于计算偏移量的卷积模块,但保留了端到端的学习能力。从时间的角度分析,仅仅增加了若干个卷积模块的复杂度,便在很大程度上提高了模型的预测精度(论文中有详细数据说明,在这里由于篇幅限制,没有展示实验结果),因此属于用(少许)时间换(大量)精度的方法,因此我认为这一思路是值得实践的。
从全局来看,这是一种具有内部参数(具体地,这里的内部参数是偏移量)、但内部参数通过数据学习的方法。因此,从理论层面上说,设计者可以感受不到这些内部参数的存在,而是将它视作简单的、无内部参数的模块去使用,尽管二者的原理并不全然相同。这一点为可变形卷积模块的推广提供了坚实的基础。理论上讲,任意模型中的卷积模块都可以替换成为可变形卷积模块。