到目前位置,我们主要把注意力集中在监督学习的问题上,数据集中的每个数据点都有一个已知的标签或者目标值。然而如果面对没有已知的输出结果,或者没有人监督学习算法,我们要怎么做。
这就是无监督学习 。
在无监督、非监督学习中了,学习过程仅使用输入数据,没有更多的指导信息,要求从这些数据中提取知识。我们已经讨论了非监督学习众多形式的一种降维。另一个普及的领域就是聚类分析。他的目的是吧数据分为相似元素组成的不同区域中。
在本章中,我们想要理解不同的聚类算法如何从简单到,无标记的数据集中提取特征。这些结构特征,可以用于特征处理,图像处理,甚至是作为无监督学习任务的预处理步骤。
作为一个具体的例子,我们将对图像进行聚类,将色彩空间降到16位数。
解决的问题
1.K-means聚类和期望最大化是什么?如何在opencv中实现这些算法。
2.如何在层次树中使用聚类算法。他带来的好处有哪些。
3.如何使用无监督学习,进行预处理,图像处理,分类。
1 理解无监督学习
无监督学习可能有很多形式,但是他们的目标总是把原始数据转化为更加丰富,更加有意义的表示,这么做可以让人们更容易理解,也可以更方便的使用机器学习算法进行解析。
无监督学习的应用包括一下应用:
1降维:他接受一个许多特征的高维度数据表示,尝试对这些数据进行压缩,以使其主要特征,可以使用少量的携带高信息量的数据来表示。
2因子分析:用于找到导致被观察的到的数据的隐含因素或者未观察到的方面。
3聚类分析:
尝试把数据分成相似元素组成的不同组。
无监督学习主要的挑战就是,如何确定一个算法是否出色,或者学习到什么有用内容,通常评估一个无监督学习算法结果的唯一方式是手动检查,并确定结果是否有意义。
话虽然如此,但是非监督学习,可以非常有,比如作为预处理或者特征提取的步骤。
2理解K-means聚类
Opencv 提供最有用的聚类算法是k-means,因为它会从一个没有标记的多维度数据集中搜寻预设的K个聚类结果。
它通过两个简单的假设来完成最佳聚类了。
1 每个聚类中心都是属于该类别的所有数据点的算术平均值
2 聚类中的每一个点相对其他聚类中心,更靠近本类别的中心。
2.1 实现第一个kmeans例子
首先,生成一个包含四个不同点集合的数据集。为了强调这是一个非监督的方法,我门在可视化将忽略哪些标签。使用matplotlib进行可视化。
import matplotlib.pyplot as plt
import pylab
from sklearn.datasets._samples_generator import make_blobs
plt.style.use('ggplot')
x,y=make_blobs(n_samples=300,centers=4,cluster_std=1.0,random_state=10)
plt.scatter(x[:,0],x[:,1],s=100)
pylab.show()
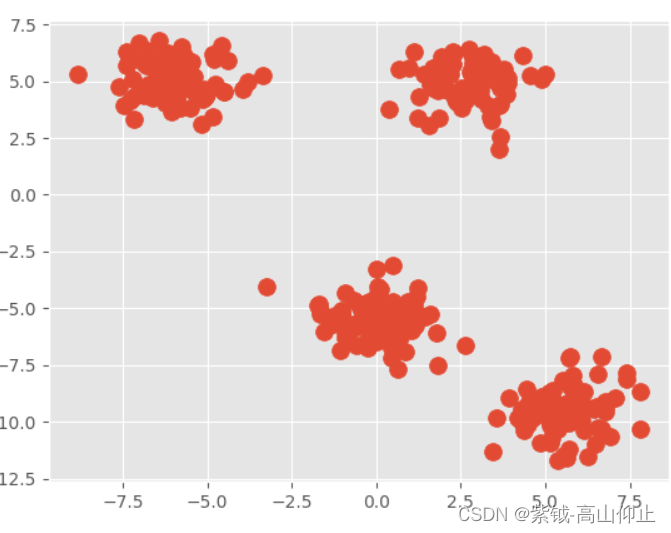
我们创建一个四个不同区域的聚类,centers=4,一共300节点。
如上程序生成图像所示结果。
尽管没有给数据分配目标标签,但直接使用肉眼还是可以看出来一共是四类。
kmeans就可以通过算法办到,无需任何关于目标的标签或者潜在的数据分布的信息。
当然尽管,kmeans在opencv中是一个统计模型,不能调用api中的train和predict。相反,使用cv2.kmeans可以直接使用这个算法。。为了使用这个模型,我们需要指定一些参数,比如终止条件,和初始化标志。
我们让算法误差小于1.0(cv2.TERM_CRITERIA_EPS),或者已经 执行了十次迭代(cv2.TERM_CITTERIA_MAX_ITER)时候终止。
import matplotlib.pyplot as plt
import pylab
from sklearn.datasets._samples_generator import make_blobs
import cv2
import numpy as np
plt.style.use('ggplot')
x,y=make_blobs(n_samples=300,centers=4,cluster_std=1.0,random_state=10)
plt.scatter(x[:,0],x[:,1],s=100)
criteria=(cv2.TERM_CRITERIA_EPS+cv2.TERM_CRITERIA_MAX_ITER,10,1.0)
flags=cv2.KMEANS_RANDOM_CENTERS
compactness,labels,centers=cv2.kmeans(x.astype(np.float32),4,None,criteria,10,flags)
print(compactness)
plt.scatter(x[:,0],x[:,1],c=labels,s=50,cmap='viridis')
plt.scatter(centers[:,0],centers[:,1],c='black',s=200,alpha=0.5)
pylab.show()
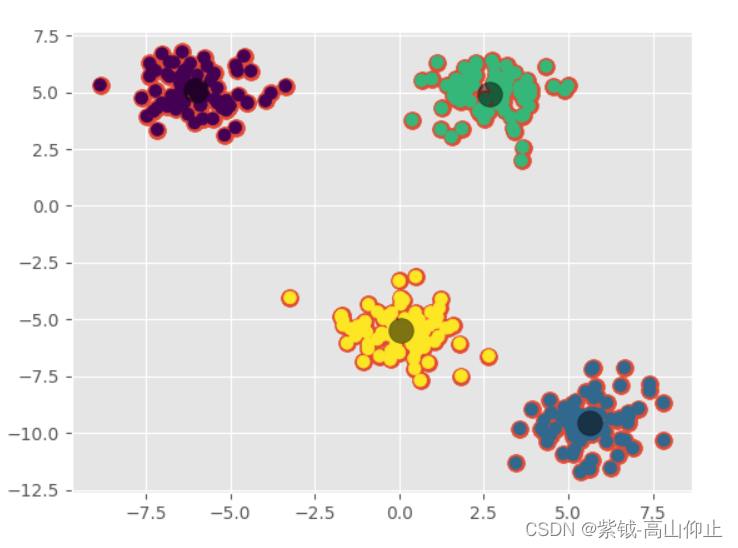
上面程序结果可以产生图2的效果。
print(compactness)这个变量,表示每个点到它聚类中心的距离平方和。较高紧凑都表明所有的点更靠近他们的聚类中心,较低 的紧凑度表明不同的聚类可能无法的很好区分。
当然,这个是非常依赖于x中的真实值。如果点与点之间最初的距离比较大,那我们就很难得到一个非常小的紧凑度。因此,把数据画出来,并按照聚类标签分配不同颜色,可以显示更多信息。
3理解kmeans
kmeans是聚类众多常见期望最大化中一个具体的例子。简单来说,算法处理的过程如下所示:
1.从一些随机的聚类中心开始
2.一种重复直到收敛
期望步骤:把所有的数据点分配到离他们最近的聚类中心。
最大化步骤:通过取出聚类中所有点的平均来更新聚类中心。
它涉及到一个定义聚类中心位置的适应性函数最大化的过程。对于kmeans最大化是计算一个聚类中所有数据点的算数平均得到。