学习内容:
9 神经网络的运用
9.1 代价函数
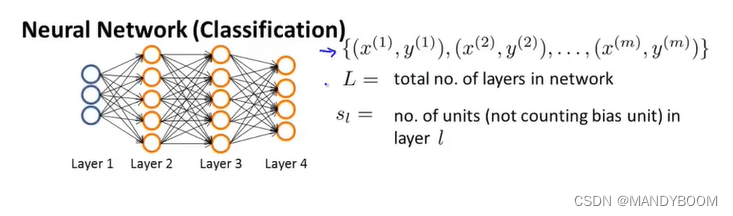
其中:
假设训练集为m组的训练样本
用L表示神经网络的总层数,对于上图来说,L=4
用表示第L层的单元数,也就是神经元的数量(不包括这一层的偏差单元)?
下面考虑两种分类问题:①二元分类;②多类分类
- ?二元分类Binary classification
? ? ? ?在二元分类中,y只能等于0或1,在这种情况下会有一个输出单元,并且输出的就是计算出来的h(x),并且它是一个实数,在这种情况下是输出单元的个数,也就是1.为了简化,设k=1,k相当于输出层的单元数目。

- 多类别分类问题Multi-class classification(K classes)?
? ? ? 假设有四类,以这四类表示y,在这种问题中会有K个输出单元(通常情况下
,因为如果只有两个类别,就不需要使用一对多的方法),假设会输出K维向量
。
下面来为神经网络定义代价函数:
? ? ? ?在神经网络中使用的代价函数是逻辑回归中使用的代价函数的一般形式,对于逻辑回归而言,通常会使代价函数最小化。
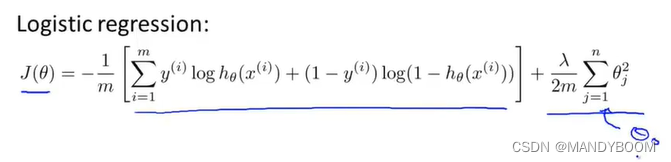
? ? ? ?对于一个神经网络来说,我们的代价函数就会是这个式子的一般形式,不再仅有一个逻辑回归输出单元,而是K个,公式如下,神经网络输出了属于的向量(?如果处理的是二元分类,K可能为1),用
表示第i个输出,代价函数也有变化,求和项从1到K。

9.2 反向传播算法
? ? ? ?可用来优化(最小化)神经网络的代价函数 ,要试图找到合适的参数,使
取到最小值,为使用到梯度下降法或其他某种高级优化算法,需要编写程序获得输入参数
,并计算代价函数
和偏导项
.

? ? ? ?假设训练样本只有一个,粗略的用这一个训练样本看看计算的顺序:首先应用前向传播方法来计算一下在给定输入的时候假设函数是否会真的输出结果,
就是第一层的激活值,
,
,其中g是一个
激活函数,这就会计算出第二层隐藏层的激活值(还增加了偏置项)。以此类推,计算出
,
,这样可以计算出神经网络中每一个神经元的激活值。?

? ? ? ?接下来,为了计算导数项,采用一种叫做反向传播(Backpropagation)的算法 ;从最后一层往前计算误差值,误差是激活单元的预测值与实际值之间的差,比如当L=4时,
,当把
都看作向量的话,也可以写作
,这样就算出了第四层的误差项,紧接着算出前几层的误差项,而要求的偏导数项恰好等于由这些激活项和误差项组成的一个函数(此时忽略正则项细节)

? 当存在大量训练样本时,计算偏导数,反向传播是如何实现的:
? ? ? ? 假设有m个样本的训练集,设置每个ij对应的,此处的
是大写的
,而这些
会被用来计算偏导项对应上下标的
的偏导数,接下来遍历训练集(1~m)?,紧接着第一件事要设激活函数为输入值,然后运用正向传播来计算第二层、第三层、……、直到最后一层L层的激活值,接下来用样本的输出值
,计算输出值对应的误差项
,利用反向传播算法来计算
(强调此处没有
,因为不需要对输入层考虑误差项),最后用大写的
来累积在前面写好的偏导数项,循环出来后接着计算
(代价函数的偏导数)。

9.3 理解反向传播?
? ? ? ?在理解反向传播前,先大致看一下前向传播过程,先假设输入样本为,计算出每一层的激活值以及权重,进而计算下一层的激活值。
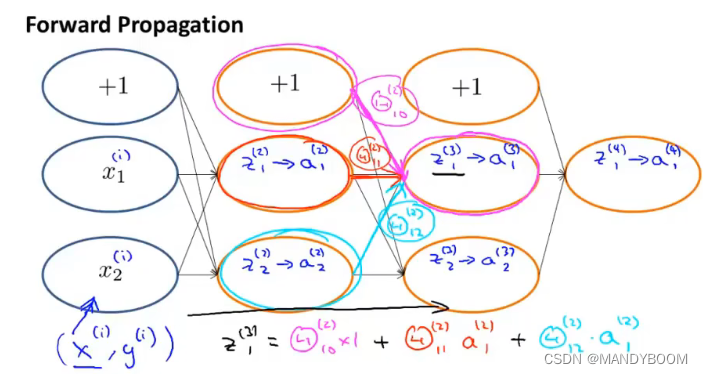
? ? ?反向传播与前向传播类似,只是计算的方向不一样而已(从右往左计算)
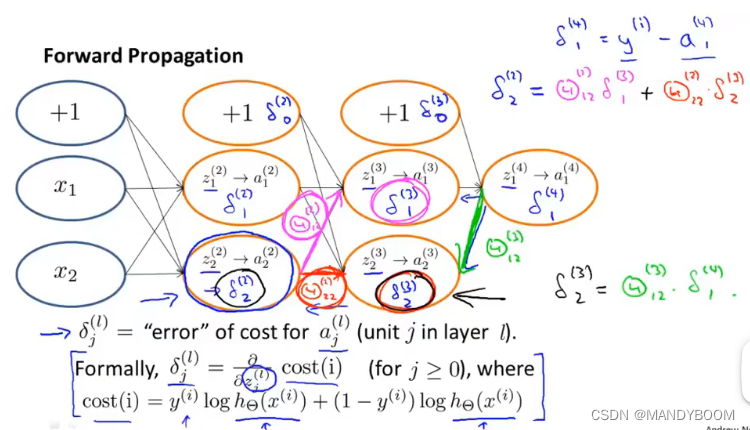
? ? ?先看一下代价函数,当只有一个输出单元的时候代价函数如下(如果不止一个输出单元,只需用k作为输出单元的下标,然后对他们进行求和即可):
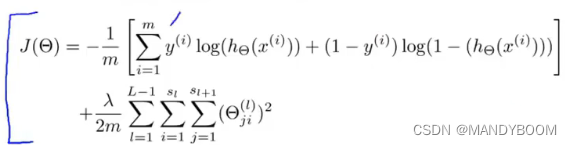
? ? ? ?忽略正则化(λ=0),所以去掉正则项剩下的部分(大括号内的),是第i个样本的代价函数
![]()
? ? ?这一部分也可近似的认为是实际值与预测值之间的方差?
? ? 接着看反向传播的过程,直观来看,反向传播算法就是在计算这些项(激活项的误差),先算出输出层的误差,反向传播算出前面每一层的误差,不包括输入层
9.4 怎样把参数从矩阵展开成向量?
将参数从矩阵展开成向量可以便于高级最优化步骤中使用。
设有三个权重矩阵:Theta1,Theta2,Theta3 。下面是将其向量化 “Unroll” into vectors,再变回矩阵的方法:
?

?9.5 梯度检测
- ?例:假设有一个代价函数
,取一点
,这一点对应的切线为这一点的导数即斜率。取
两边两点
在图上对应点,连接起来的直线斜率尽可能逼近
对应的斜率。
? ? ? ? 其中点对应的斜率为
,红色的两点间直线的斜率为
,
是足够小的一个数。
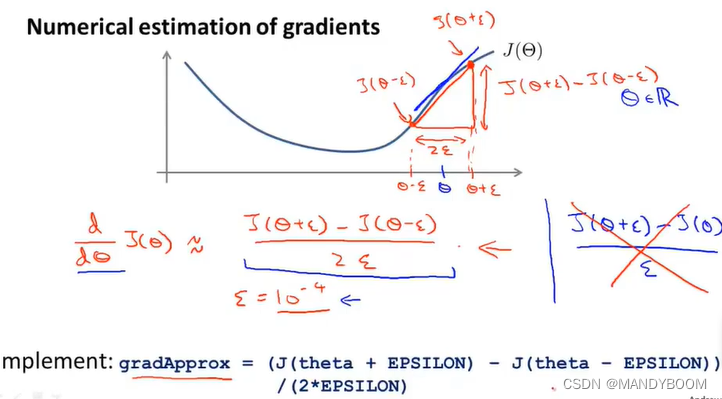
? ? ?刚刚只考虑了是实数的情况,当
为向量参数的时候,设
为一个n维向量,可以向上面一样计算每个参数的偏导数

上述算法如下:
 ? ? ? ?最好要验证计算出来的导数在数值上是否非常接近于反向传播所计算出的导数DVec,如果计算出来的导数是一样的,或者说非常接近,只有几位小数的差距,就可以确定反向传播的实现是正确的。那么当把DVec用到梯度下降或者其他高级优化算法中时,就可以确定计算的导数是正确的,也能很好的优化
? ? ? ?最好要验证计算出来的导数在数值上是否非常接近于反向传播所计算出的导数DVec,如果计算出来的导数是一样的,或者说非常接近,只有几位小数的差距,就可以确定反向传播的实现是正确的。那么当把DVec用到梯度下降或者其他高级优化算法中时,就可以确定计算的导数是正确的,也能很好的优化.

?只在测试的时候进行校验。真正使用 back propagation 进行神经网络学习的时候,要停止校验,否则会非常慢。
9.6 随机初始化?
? ? ? ?当执行一个算法,例如梯度下降法或高级优化算法,需要为变量选取一些初始值,对于高级优化算法会默认会给
赋初值,对于梯度下降算法,同样也要对
初始化,初始化完毕后,就可以一步一步通过梯度下降来最小化代价函数。
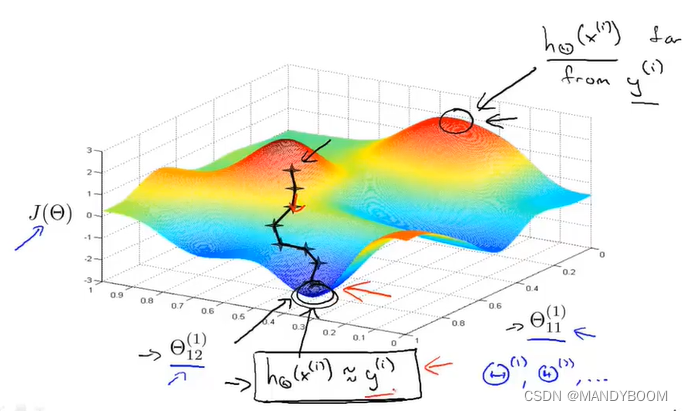
? ? ??的初始化可以全部设为0,但通常在训练的过程中,初始化为0起不到任何作用,以下面的神经网络为例,初始化θ都为0,就意味着所有蓝线红线绿线上的权重都相同,那么隐藏层上的激活单元都是以同一输入函数来计算的,那么最终总能得到
相同,误差也相等,那么相同颜色的偏导数也都相同,那么梯度下降完成后,得到的新参数还相等,继续梯度下降还相等,那么这个神经网络计算出的结果就没意义(高度冗余现象,所有单元都在计算同样的输入函数)。所以要用随机初始化的思想对θ赋值。
随机初始化:将参数θ初始化为中的随机值,所以参数的权重将会被随机初始化为

9.7 神经网络综合运用??
- 选择神经网络架构(神经元之间的连接模式):每个隐藏层通常都有相同的个隐藏单元,通常情况下,最左边的模型为合理的模型,但对于隐藏单元的个数则是越多越好(还得与特征x数量相匹配,可相等,也可以大几倍)。
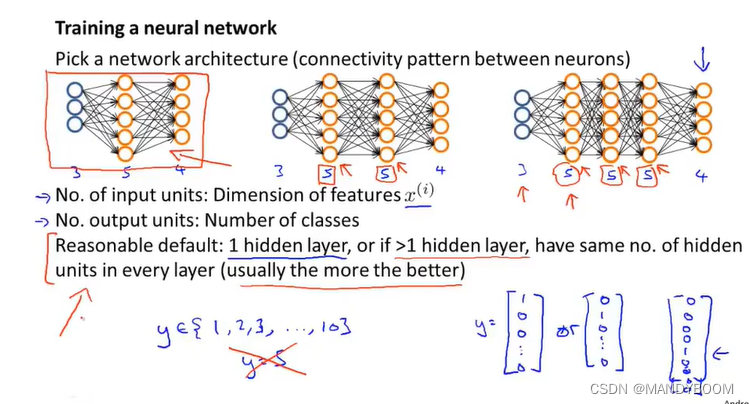
- 训练一个神经网络:
- 随机初始化权重,通常会初始化为很小的值,接近于零
- 执行前向传播算法,也就是对神经网络任意输入
- 通过代码计算出代价函数J(θ)
- 执行反向传播算法计算出偏导数
- 梯度检查,将用反向传播算法计算出来的导数与用数值方法得到的估计值进行比较,确保两个值接近,然后停用梯度检查(否则下面会非常慢)
- 使用一个最优化算法(梯度下降或高级优化算法),用反向传播算出来的偏导数和参数θ最优化代价函数
- ?神经网络的直观表示如下,因为J(𝜃)不是一个凸函数,因此我们可以到达一个局部最小点。