一：谱聚类与图划分

无向图切图：谱聚类算法根据数据点之间的相似度将数据点划分到不同簇中，因此将数据点映射到无向图之后，可以转化为图划分的问题。对于无向图 $G$ ，切图的目标是将图 $G (V, E)$ 切分成互相无连接 $k$ 个子图，其中

每个子图点的集合为 ${A_{1},A_{2},...,A_{k}\}$ ，且满足 $A_{i}\cap A_{j}=\empty$ 、 $A_{1}\cup A_{2}\cup ... \cup A_{k}=V$
对于任意两个子图点的集合 $A$ 、 $B$ ，我们定义 $A$ 和 $B$ 之间的切图权重为 $W(A,B)=\sum\limits_{i\in A,j \in B} w_{ij}$
对于 $k$ 个子图点的集合 ${A_{1},A_{2},...,A_{k}\}$ ，定义切图 $cut(A_{1},A_{2},...,A_{k})=\frac{1}{2}\sum\limits_{i=1}^{k}W(A_{i},\bar A_{i})$ （其中 $\bar A_{i}$ 为 $A_{i}$ 的补集）

可以看出， $c u t$ 描述了子图之间的相似性， $c u t$ 越小那么子图的差异性就越大。但是 $cut(A_{1},A_{2},...,A_{k})=\frac{1}{2}\sum\limits_{i=1}^{k}W(A_{i},\bar A_{i})$ 在划分子图时并没有考虑每个子图中节点的个数。所以在某些情况下，最小化 $cut(A_{1},A_{2},...,A_{k})$ 可能会把一个数据点或是很少数据点看做一个子图，导致子图划分结果不平衡

例如下图，选择一个权重最小的边缘的点，比如 $C$ 和 $H$ 之间进行 $c u t$ ，这样可以最小化 $cut(A_{1},A_{2},...,A_{k})$ 但是却不是最优的切图

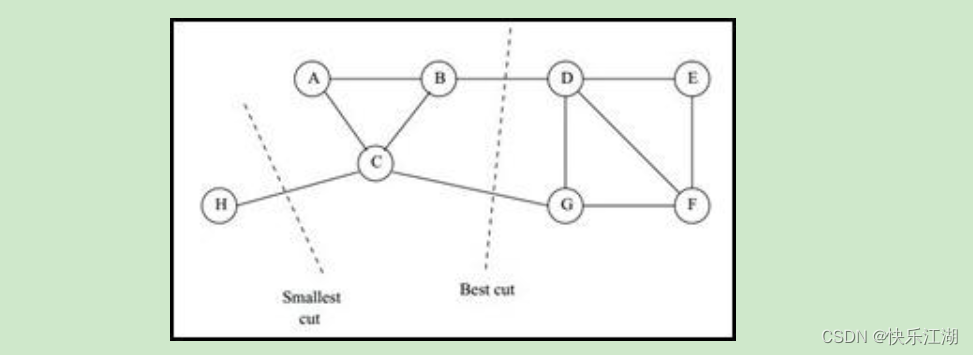
在这里插入图片描述
为了解决这个问题，会引入一些正则化方法。最常用的两种方法为比例割和规范割

比例割： $Ratiocut(A_{1},A_{2},...,A_{k})=\frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_{i},\bar A_{i})}{|A_{i}|}$
规范割： $NCut(A_{1},A_{2},...,A_{k})=\frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_{i},\bar A_{i})}{vol(A _{i})}$

（1）比例割

引入指示向量（点击可查看指示向量定义） $h_{j}\in\{h_{1},h_{2},...,h_{k}\}$ ， $j = 1, 2, ..., k$ 。对于任意一个向量 $h_{j}$ ，它是一个 $n$ 维向量（ $n$ 表示样本数），定义 $h_{ij}$ 如下

$h_{ij}=\begin{cases} 0，v_{i}\notin A_{j}\\ \sqrt{|A_{j}|}，v_{i}\in A_{j}\\ \end{cases}$

于是，对于 $h_{i}^{T}Lh_{i}$ ，根据拉普拉斯矩阵性质可知

对于任意向量 $f=(f_{1},...,f_{n})^{T} \in R^{n}$ ，有 $f^{T}Lf=\frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(f_{i}-f_{j})^{2}$

$h_{i}^{T}Lh_{i}=\frac{1}{2}\sum\limits_{m=1}\sum\limits_{n=1}w_{mn}(h_{im}-h_{in})^{2}=\frac{cut(A_{i},\bar A_{i})}{|A_{i}|}$

严格证明过程请看刘建平博客：链接

可以看到，对于某一个子图 $i$ ， $R a t i o n C u t$ 就对应于 $h_{i}^{T}Lh_{i}$ ，那么对于 $k$ 个子图

$RatioCut(A_{1},A_{2},...,A_{k})=\sum\limits_{i=1}^{k}h_{i}^{T}Lh_{i}=\sum\limits_{i=1}^{k}(H^{T}LH)_{ii}=tr(H^{T}LH)$

因此， $R a t i o n C u t$ 切图本质就是最小化 $tr(H^{T}LH)$ 。又因为 $H^{T}H=I$ （单位矩阵），则切图优化目标为

$\underbrace{argmin}_{H} tr(H^{T}LH) s.t.H^{T}H=I$

对于优化目标 $tr(H^{t}LH)$ 中的每一个优化子目标 $h_{i}^{T}Lh_{i}$ ，其中的 $h$ 是单位正交基， $L$ 为对称矩阵，所以此时 $h_{i}^{T}Lh_{i}$ 的最大值即为 $L$ 的最大特征值、最小值即为 $L$ 的最小特征值。而在谱聚类中，我们的目标就是要找到目标的最小特征值，得到对应特征值向量，此时切图效果最佳。所以对于 $h_{i}^{T}Lh_{i}$ ，目标就是找到 $L$ 的最小特征值，而对于 $tr(H^{t}LH)=\sum\limits_{i=1}^{k}h_{i}^{T}Lh_{i}$ ，则目标就是要找到 $k$ 个最小的特征值

因此，通过找到 $L$ 的最小的 $k$ 个特征值，可以得到对应的 $k$ 个特征向量，这 $k$ 特特征向量组成一个 $n$ × $k$ 维矩阵，也即 $H$ 。一般需要对矩阵 $H$ 按行做标准化，如下

一般来说， $k$ 远小于 $n$ ，也就说进行了降维

$h_{ij}^{*}=\frac{h_{ij}}{(\sum\limits_{t=1}^{k}h_{it}^2)^{\frac{1}{2}}}$

这里需要注意，降维后导致得到的指示向量 $h$ 对应的 $H$ 现在并不能完全指示各样本的归属，因此一般在得到 $n \times k$ 维的矩阵 $H$ 后还需要对每一行进行一次传统的聚类，比如使用K-Means聚类

（2）规范割（常用）

规范割和比例割类似，只是把比例割的分母 $A_{i}|$ 换成了 $vol(A_{i})$ ，定义指示向量 $h_{ij}$ 如下

$h_{ij}=\begin{cases} 0，v_{i}\notin A_{j}\\ \sqrt{vol(A_{i})}，v_{i}\in A_{j}\\ \end{cases}$

于是，对于 $h_{i}^{T}Lh_{i}$ ，根据拉普拉斯矩阵性质可知

对于任意向量 $f=(f_{1},...,f_{n})^{T} \in R^{n}$ ，有 $f^{T}Lf=\frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(f_{i}-f_{j})^{2}$

$h_{i}^{T}Lh_{i}=\frac{1}{2}\sum\limits_{m=1}\sum\limits_{n=1}w_{mn}(h_{im}-h_{in})^{2}=\frac{cut(A_{i},\bar A_{i})}{vol(A_{i})}$

严格证明过程请看刘建平博客：链接

可以看到，对于某一个子图 $i$ ， $R a t i o n C u t$ 就对应于 $h_{i}^{T}Lh_{i}$ ，那么对于 $k$ 个子图

$NCut(A_{1},A_{2},...,A_{k})=\sum\limits_{i=1}^{k}h_{i}^{T}Lh_{i}=\sum\limits_{i=1}^{k}(H^{T}LH)_{ii}=tr(H^{T}LH)$

但此时 $H^{T}H \not=I$ ，而是 $H^{T}DH =I$

这是因为 $h_{i}^{T}Dh_{i}=\sum\limits_{j=1}^{n}h_{ij}^{2}d_{j}=\frac{1}{vol(A_{i})}\sum\limits_{j\in A_{i}}d_{j}=\frac{1}{vol(A_{i})}vol(A_{i})=1$

因此，此时切图优化目标为

$\underbrace{argmin}_{H} tr(H^{T}LH) s.t.H^{T}DH=I$

但是现在矩阵 $H$ 中的指示向量 $h$ 并不是标准正交基，所以需要对 $H$ 做一定转换。令 $H=D^{-\frac{1}{2}}F$ ，则 $H^{T}LH=F^{T}D^{-\frac{1}{2}}LD^{-\frac{1}{2}}F$ 、 $H^{T}DH=F^{T}F=I$ ，于是优化目标变更为
$\underbrace{argmin}_{F} tr(F^{T}D^{-\frac{1}{2}}LD^{-\frac{1}{2}}F) s.t.F^{T}F=I$

现在，和比例割一样，通过找到 $D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$ （就是之前的 $L$ ）的最小的 $k$ 个特征值，可以得到对应的 $k$ 个特征向量，这 $k$ 特征向量组成一个 $n$ × $k$ 维矩阵，也即 $F$ ，最后对 $F$ 进行传统聚类

一般来说， $D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$ 相当于对 $L$ 做了一次标准化，也即 $\frac{L_{ij}}{\sqrt{d_{i}*d_{j}}}$

二：谱聚类算法流程

给定数据集 $D=\{x_{1}, x_{2}, ... , x_{n}\}$

根据输入的相似矩阵生成方式（一般为高斯核函数）构建相似矩阵 $S$ （AffinityMatrix）
根据相似矩阵 $S$ 构建邻接矩阵 $W$ ，再构建度矩阵 $D$
计算拉普拉斯矩阵 $L = D ? W$
得到标准化后的拉普拉斯矩阵 $D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$
计算 $D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$ 最小的 $k$ 个特征值对应的特征向量 $f$
将特征向量 $f$ 组成矩阵并按行标准化，最终组成 $n$ × $k$ 维的特征矩阵 $F$
$F$ 中每一行作为一个 $k$ 维的样本，共 $n$ 个样本，采用某种聚类方法进行聚类，假设聚类维数为 $k^{、}$
得到簇划分C $c_{1}, c_{2}, ... , c_{k^{、}})$

三：Python实现

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.datasets import make_blobs
from sklearn.preprocessing import normalize

def get_affinity_matrix(data_set):
    #  利用高斯核函数计算相似矩阵(全连接)
    rbf = rbf_kernel(data_set)
    for i in range(len(rbf)):
        rbf[i, i] = 0
    return rbf


def distance(x1, x2):
    """
    获得两个样本点之间的距离
    :param x1: 样本点1
    :param x2: 样本点2
    :return:
    """
    dist = np.sqrt(np.power(x1-x2,2).sum())
    return dist

def get_dist_matrix(data):
    """
    获取距离矩阵
    :param data: 样本集合
    :return: 距离矩阵
    """
    n = len(data)  #样本总数
    dist_matrix = np.zeros((n, n)) # 初始化邻接矩阵为n×n的全0矩阵
    for i in range(n):
        for j in range(i+1, n):
            dist_matrix[i][j] = dist_matrix[j][i] = distance(data[i], data[j])
    return dist_matrix

def get_W(data, k):
    # 获取邻接矩阵（K邻近法）
    n = len(data)
    dist_matrix = get_dist_matrix(data)
    W = np.zeros((n, n))
    for idx, item in enumerate(dist_matrix):
        idx_array = np.argsort(item)  # 每一行距离列表进行排序,得到对应的索引列表
        W[idx][idx_array[1:k+1]] = 1
    transpW =np.transpose(W)
    return (W+transpW)/2

def spectral_clustering(data_set, k):
    # 利用相似矩阵S得到邻接矩阵W
    W = get_affinity_matrix(data_set)  #高斯核函数（全连接法）
    #  W = get_W(data_set, k)  # K邻近法

    # 计算度矩阵D,并得到矩阵D的1/2次方的逆矩阵（便于计算拉普拉斯矩阵）
    D_inv = np.diag(np.power(np.sum(W, axis=1), -0.5))

    # 计算拉普拉斯矩阵L=D-W
    # 标准化拉普拉斯矩阵l = D_inv*L*D_inv=I-D_inv*W*D_inv
    L = np.eye(len(data_set)) - np.dot(np.dot(D_inv, W), D_inv)

    # 得到特征值和特征向量
    eigvals, eigvecs = np.linalg.eig(L)

    # 找到前k个最小的特征值（索引）
    k_smallest_eigvals_index = np.argsort(eigvals)[:k]

    # 取出这k小特征值对应的特征向量，并正则化
    k_smallest_eigvecs = normalize(eigvecs[:, k_smallest_eigvals_index])
    
    # 使用K_Means聚类
    return KMeans(n_clusters=k).fit_predict(k_smallest_eigvecs)


raw_data = pd.read_csv(r'E:\Postgraduate\Dataset\jain.csv', header=None)
raw_data.columns = ['X', 'Y']
x_axis = 'X'
y_axis = 'Y'

examples_num = raw_data.shape[0]
train_data = raw_data[[x_axis, y_axis]].values.reshape(examples_num, 2)


min_vals = train_data.min(0)
max_vals = train_data.max(0)
ranges = max_vals - min_vals
normal_data = np.zeros(np.shape(train_data))
nums = train_data.shape[0]
normal_data = train_data - np.tile(min_vals, (nums, 1))
normal_data = normal_data / np.tile(ranges, (nums, 1))

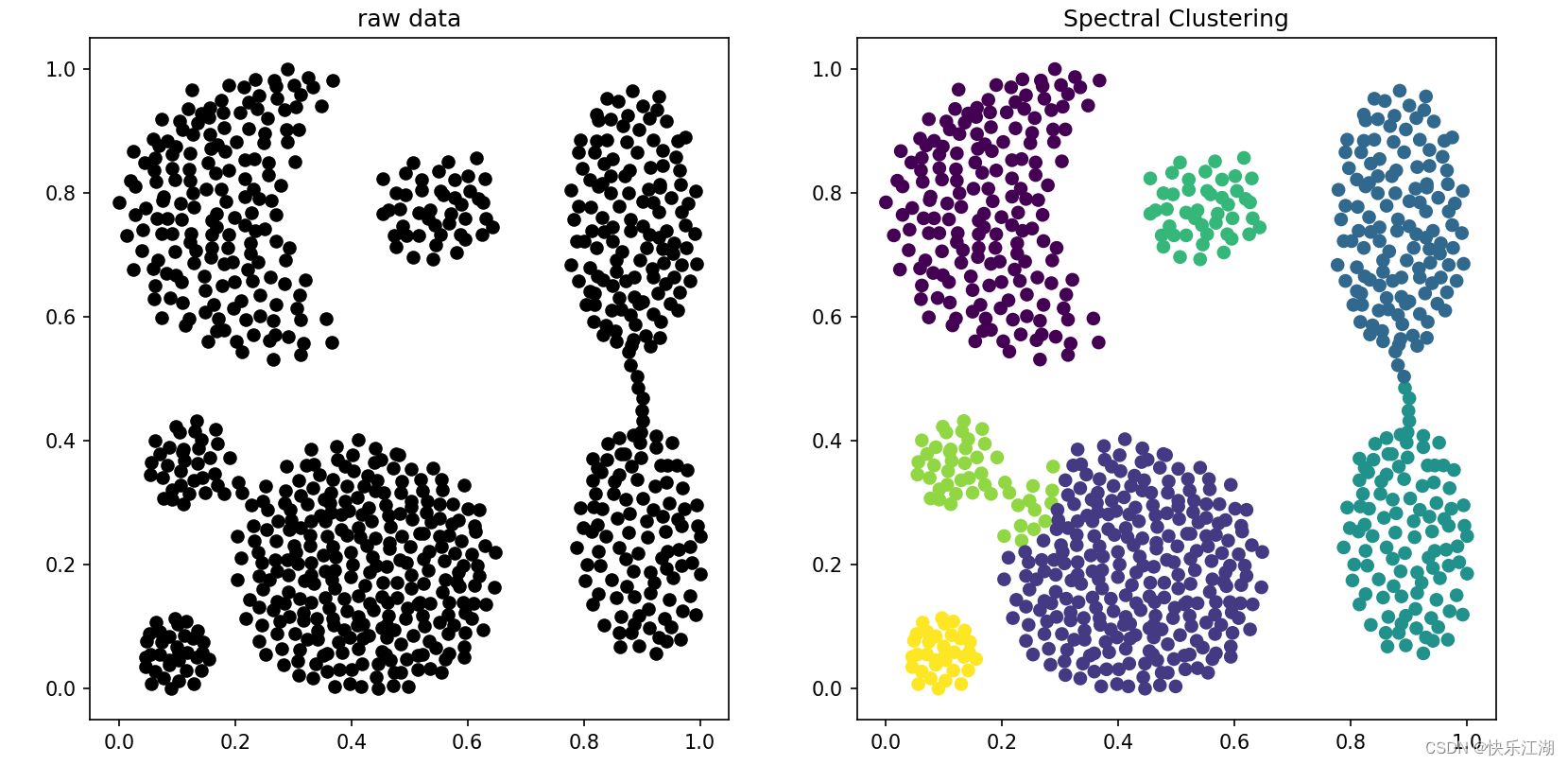
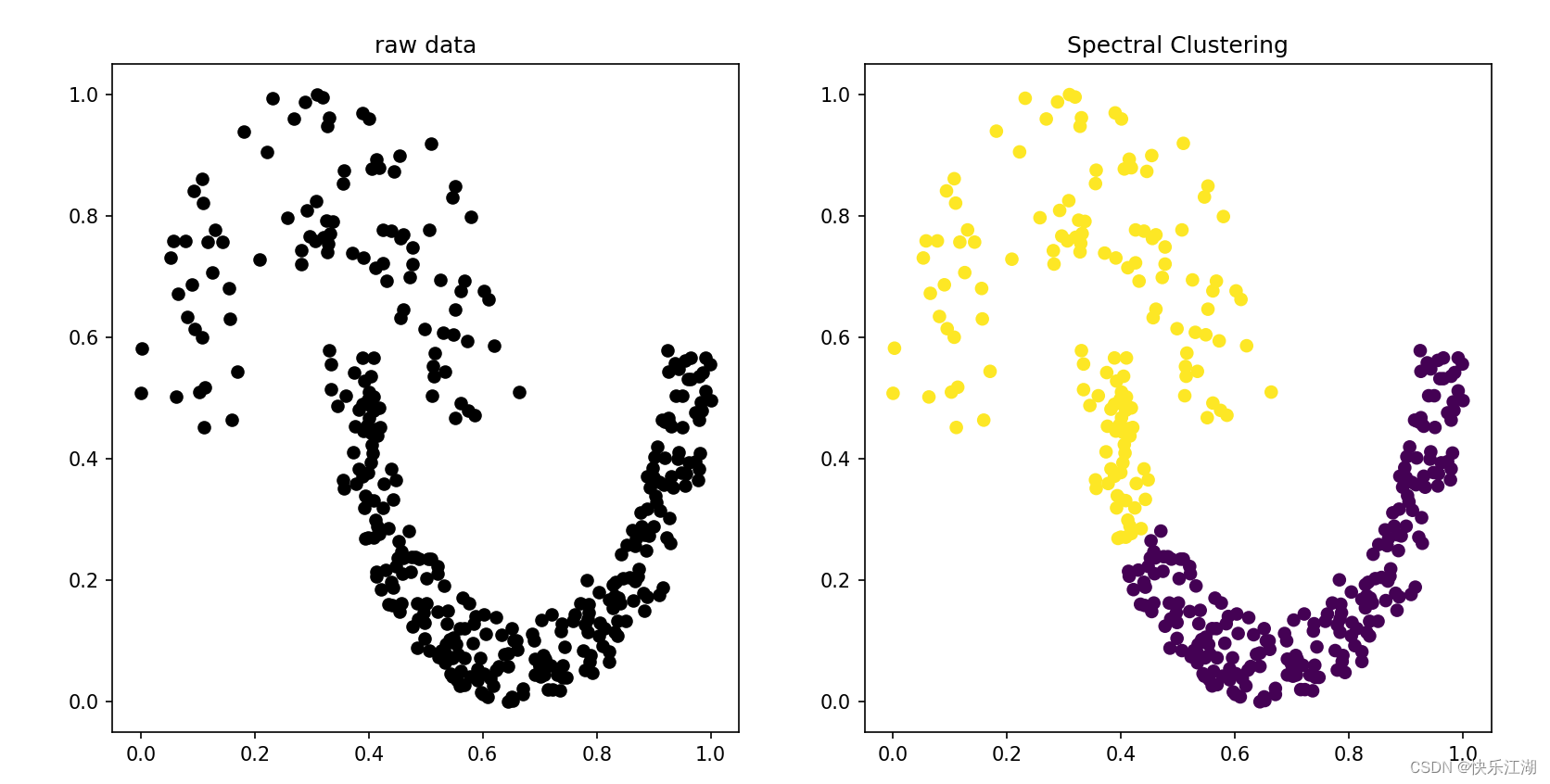
labels = spectral_clustering(normal_data, 2)

# 原数据
fig, (ax0, ax1) = plt.subplots(ncols=2)
ax0.scatter(normal_data[:, 0], normal_data[:, 1], c='black')
ax0.set_title('raw data')
# 谱聚类结果
ax1.scatter(normal_data[:, 0], normal_data[:, 1], c=labels)
ax1.set_title('Spectral Clustering')

plt.show()