[人工智能] 广告行业中那些趣事系列57：从理论到实战一网打尽Transformer中的位置编码

导读：本文是“数据拾光者”专栏的第五十七篇文章，这个系列将介绍在广告行业中自然语言处理和推荐系统实践。本篇从理论到实践介绍了Transformer中的位置编码，包括训练式位置编码、三角函数式位置编码和相对位置编码，同时基于开源项目bert4keras源码实践了各种位置编码。

欢迎转载，转载请注明出处以及链接，更多关于自然语言处理、推荐系统优质内容请关注如下频道。

知乎专栏：数据拾光者

公众号：数据拾光者

摘要：本篇从理论到实践介绍了Transformer中的位置编码。首先介绍了位置编码的作用以及主要实现方式；然后重点介绍了主流的位置编码方式，包括训练式位置编码、三角函数式位置编码和相对位置编码，同时基于开源项目bert4keras源码实践了各种位置编码。对Transformer中位置编码的知识和源码实践感兴趣的小伙伴可以多交流。

下面主要按照如下思维导图进行学习分享：

位置编码背景介绍

1.1?为什么需要位置编码

BERT作为NLP领域中里程碑式的模型，不仅效果好而且应用范围广，最重要的原因是使用Transformer作为特征抽取器。Transformer相比于传统的CNN和RNN来说，整个网络主要由Attention机制组成，同时具有可并行化计算和捕捉长距离特征的优点，是目前公认效果最好的特征抽取器之一。对于Transformer来说位置编码是非常重要的，主要原因有以下两个：

词在语句中的位置非常重要。使用同样的词语，排列位置不同，语义可能不同，比如：“我喜欢刘亦菲”和“刘亦菲喜欢我”表达的语义差别很大；
Transformer主要核心是attention注意力机制，attention机制可以计算当前词对其他词的注意力得分，但无法捕捉词顺序，类似一个升级版的“词袋”模型。

1.2 更通俗的理解位置编码

因为Transformer模型不具备RNN学习词序的能力，所以需要将词序信息提供给模型。原来输入到模型中的是词信息，现在需要将词信息和位置信息融合之后输入到模型中，所以位置编码可以看成是利用词的位置信息对语句中的词进行二次表示的方法，通过位置编码使得Transformer模型具备了学习词序的能力。

1.3 实现位置编码的主要方式

想让Transformer具备学习词序信息的能力，一般有两种做法：第一种是将位置信息融合到模型输入，这种主要是绝对位置编码，主要代表是BERT和GPT等模型；第二种是微调Attention结构使其获得识别词序信息的能力，这种主要是相对位置编码。

训练式位置编码

训练式位置编码的典型代表就是BERT、GPT等模型，将位置编码添加到输入中，比如下面的BERT模型输入，会将文本序列转化成三层embedding作为Transformer模型的输入，第一层embedding是词信息token embedding，第二层是segment embedding，第三层则是位置编码信息position embedding。下面是将文本转化成三层embedding作为BERT模型输入介绍图：

图1 文本转化成三层embedding作为BERT模型输入

将位置编码和词token一样作为可以训练的参数，比如最大长度设置为512，向量维度设置为768，那么一条语句就会得到512X768的矩阵作为初始向量，并随着训练进行更新。训练式位置编码的优点是简单容易实现，缺点则是没有外推性。比如原生BERT最长只能处理512长度的语句，如果任务中文本大于512则会进行截断操作。最近调研到苏神通过层次分解可以让BERT处理足够长的文本，并且效果还不错，感兴趣的小伙伴可以查看参考资料1。

下面是开源工程bert4keras训练式位置编码的源码实现：

class PositionEmbedding(Layer):
    """定义可训练的位置Embedding
    """
    def __init__(
        self,
        input_dim,
        output_dim,
        merge_mode='add',
        hierarchical=None,
        embeddings_initializer='zeros',
        custom_position_ids=False,
        **kwargs
    ):
        super(PositionEmbedding, self).__init__(**kwargs)
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.merge_mode = merge_mode
        self.hierarchical = hierarchical
        self.embeddings_initializer = initializers.get(embeddings_initializer)
        self.custom_position_ids = custom_position_ids


    def build(self, input_shape):
        super(PositionEmbedding, self).build(input_shape)
        self.embeddings = self.add_weight(
            name='embeddings',
            shape=(self.input_dim, self.output_dim),
            initializer=self.embeddings_initializer
        )


    def call(self, inputs):
        """如果custom_position_ids，那么第二个输入为自定义的位置id
        """
        if self.custom_position_ids:
            inputs, position_ids = inputs
            if 'int' not in K.dtype(position_ids):
                position_ids = K.cast(position_ids, 'int32')
        else:
            input_shape = K.shape(inputs)
            batch_size, seq_len = input_shape[0], input_shape[1]
            position_ids = K.arange(0, seq_len, dtype='int32')[None]


        if self.hierarchical:
            alpha = 0.4 if self.hierarchical is True else self.hierarchical
            embeddings = self.embeddings - alpha * self.embeddings[:1]
            embeddings = embeddings / (1 - alpha)
            embeddings_x = K.gather(embeddings, position_ids // self.input_dim)
            embeddings_y = K.gather(embeddings, position_ids % self.input_dim)
            embeddings = alpha * embeddings_x + (1 - alpha) * embeddings_y
        else:
            if self.custom_position_ids:
                embeddings = K.gather(self.embeddings, position_ids)
            else:
                embeddings = self.embeddings[None, :seq_len]


        if self.merge_mode == 'add':
            return inputs + embeddings
        elif self.merge_mode == 'mul':
            return inputs * (embeddings + 1.0)
        elif self.merge_mode == 'zero':
            return embeddings
        else:
            if not self.custom_position_ids:
                embeddings = K.tile(embeddings, [batch_size, 1, 1])
            return K.concatenate([inputs, embeddings])


    def compute_output_shape(self, input_shape):
        if self.custom_position_ids:
            input_shape = input_shape[0]


        if self.merge_mode in ['add', 'mul', 'zero']:
            return input_shape[:2] + (self.output_dim,)
        else:
            return input_shape[:2] + (input_shape[2] + self.output_dim,)


    def get_config(self):
        config = {
            'input_dim': self.input_dim,
            'output_dim': self.output_dim,
            'merge_mode': self.merge_mode,
            'hierarchical': self.hierarchical,
            'embeddings_initializer':
                initializers.serialize(self.embeddings_initializer),
            'custom_position_ids': self.custom_position_ids,
        }
        base_config = super(PositionEmbedding, self).get_config()
        return dict(list(base_config.items()) + list(config.items()))

三角函数式位置编码

三角函数式位置编码是谷歌在论文《Attention is All You Need》所提出来的一个显式解。训练式位置编码的做法是线性分配一个数值给每个时间步，比如语句中第一个词分配的初始位置编码为1，第二个词分配为2，以此类推，直到最后一个词分配为语句长度N。这种位置编码会存在一定的问题，一方面当序列很长时会使分配的数值非常大；另一方面模型可能会遇到和训练中长度不同的语句，这里可能是更长或者更短的样本，会严重影响模型的泛化能力。

为了解决训练式位置编码存在的问题，Transformer的作者提出了一种简单但是创新的位置编码-三角函数式位置编码。三角函数式位置编码满足以下四个特点：

语句中每个词的位置编码是唯一的；
不同长度的句子中任意相邻两个词的距离是一致的；
模型可以很容易处理更长的语句，并且值有界；
位置编码是确定性的。

三角函数式位置编码不是一个单一的数值，而是一个类似词向量的d维向量，通过注入词的顺序信息来增强模型输入。下面通过公式理解三角函数式位置编码，给定一个长度n的语句，t表示词在语句中的位置，Pt则表示位置t对应的位置向量，d代表向量的维度。Pt公式定义如下：

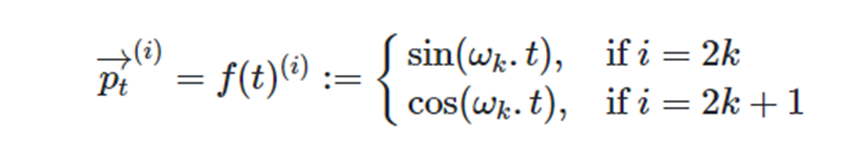
图2 三角函数式位置编码公式

其中频率Wk定义如下：

从公式中可以看出位置编码Pt是一个包含各频率的正弦和余弦对，展开表示如下：

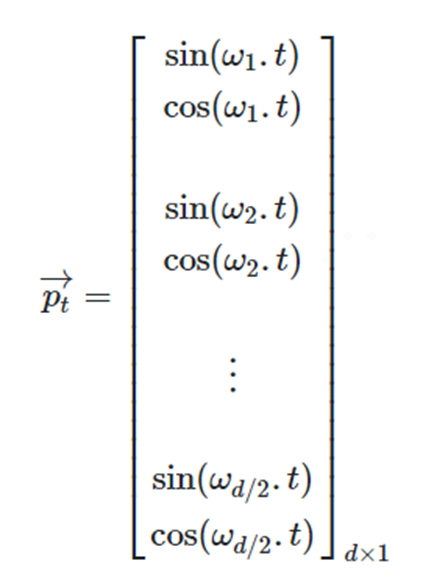
图3 位置编码Pt展开表示

位置t对应的三角函数位置编码是d维向量，其中d是双数。这里有个问题，为什么要通过sin和cos函数来表示位置编码？如果通过one-hot编码来表示位置，则如下图所示：

图4 one-hot表示位置编码

One-hot编码存在高维稀疏问题，为了节约空间使用sin-cos函数。假如有50个词，每个词的位置编码有128维，三角函数的值域空间是【-1,1】，值从小到大颜色从红色到蓝色，下面是每行代表每个词的位置编码cos/sin函数图：

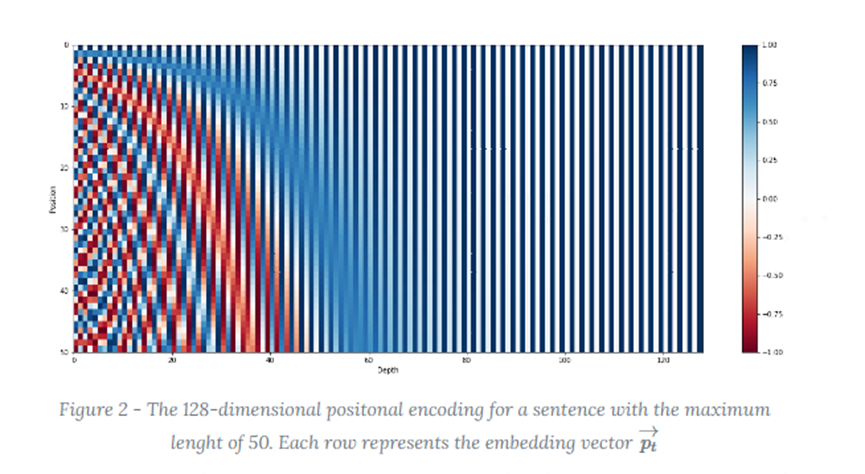
图5 每个词的位置编码cos/sin函数图

下面是开源工程bert4keras三角函数式位置编码的源码实现：

class SinusoidalPositionEmbedding(Layer):
    """定义Sin-Cos位置Embedding
    """
    def __init__(
        self,
        output_dim,
        merge_mode='add',
        custom_position_ids=False,
        **kwargs
    ):
        super(SinusoidalPositionEmbedding, self).__init__(**kwargs)
        self.output_dim = output_dim
        self.merge_mode = merge_mode
        self.custom_position_ids = custom_position_ids


    def call(self, inputs):
        """如果custom_position_ids，那么第二个输入为自定义的位置id
        """
        if self.custom_position_ids:
            seq_len = K.shape(inputs)[1]
            inputs, position_ids = inputs
            if 'float' not in K.dtype(position_ids):
                position_ids = K.cast(position_ids, K.floatx())
        else:
            input_shape = K.shape(inputs)
            batch_size, seq_len = input_shape[0], input_shape[1]
            position_ids = K.arange(0, seq_len, dtype=K.floatx())[None]


        indices = K.arange(0, self.output_dim // 2, dtype=K.floatx())
        indices = K.pow(10000.0, -2 * indices / self.output_dim)
        embeddings = tf.einsum('bn,d->bnd', position_ids, indices)
        embeddings = K.stack([K.sin(embeddings), K.cos(embeddings)], axis=-1)
        embeddings = K.reshape(embeddings, (-1, seq_len, self.output_dim))


        if self.merge_mode == 'add':
            return inputs + embeddings
        elif self.merge_mode == 'mul':
            return inputs * (embeddings + 1.0)
        elif self.merge_mode == 'zero':
            return embeddings
        else:
            if not self.custom_position_ids:
                embeddings = K.tile(embeddings, [batch_size, 1, 1])
            return K.concatenate([inputs, embeddings])


    def compute_output_shape(self, input_shape):
        if self.custom_position_ids:
            input_shape = input_shape[0]


        if self.merge_mode in ['add', 'mul', 'zero']:
            return input_shape[:2] + (self.output_dim,)
        else:
            return input_shape[:2] + (input_shape[2] + self.output_dim,)


    def get_config(self):
        config = {
            'output_dim': self.output_dim,
            'merge_mode': self.merge_mode,
            'custom_position_ids': self.custom_position_ids,
        }
        base_config = super(SinusoidalPositionEmbedding, self).get_config()
        return dict(list(base_config.items()) + list(config.items()))

相对位置编码

相对位置编码是谷歌的论文《Self-Attention with Relative Position Representations》中提出来的，典型代表是华为开源的NEZHA模型。因为语句中词与词之间相对位置非常重要，所以相对位置编码在自然语言处理任务中也有不错的表现。

相对位置编码由绝对位置编码启发得到，下面是相对位置编码的推导公式：

图6 相对位置编码推导公式

上图中左上角是self-attention的计算公式，将qikjT展开，为了引入相对位置，把piWQ去掉，把pjWk转换为二元位置向量RijK，同时将pjWv替换成二元位置向量RijV。通过这种转换，将原来依赖二元坐标(i,j)的向量RijK和RijV改成只依赖于相对位置i-j。同时为了适应任意不同的距离，会进行截断操作，也就是如下公式：

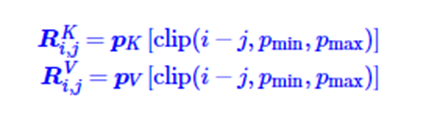
因为进行了截断操作，只需要有限个位置编码，就可以表达出任意长度的相对位置，所以可以处理任意长度的文本数据。

下面是开源工程bert4keras相对位置编码的源码实现：

class RelativePositionEmbedding(Layer):
    """相对位置编码
    来自论文：https://arxiv.org/abs/1803.02155
    """
    def __init__(
        self, input_dim, output_dim, embeddings_initializer='zeros', **kwargs
    ):
        super(RelativePositionEmbedding, self).__init__(**kwargs)
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.embeddings_initializer = initializers.get(embeddings_initializer)


    def build(self, input_shape):
        super(RelativePositionEmbedding, self).build(input_shape)
        self.embeddings = self.add_weight(
            name='embeddings',
            shape=(self.input_dim, self.output_dim),
            initializer=self.embeddings_initializer,
        )


    def call(self, inputs):
        pos_ids = self.compute_position_ids(inputs)
        return K.gather(self.embeddings, pos_ids)


    def compute_position_ids(self, inputs):
        q, v = inputs
        # 计算位置差
        q_idxs = K.arange(0, K.shape(q)[1], dtype='int32')
        q_idxs = K.expand_dims(q_idxs, 1)
        v_idxs = K.arange(0, K.shape(v)[1], dtype='int32')
        v_idxs = K.expand_dims(v_idxs, 0)
        pos_ids = v_idxs - q_idxs
        # 后处理操作
        max_position = (self.input_dim - 1) // 2
        pos_ids = K.clip(pos_ids, -max_position, max_position)
        pos_ids = pos_ids + max_position
        return pos_ids


    def compute_output_shape(self, input_shape):
        return (None, None, self.output_dim)


    def compute_mask(self, inputs, mask):
        return mask[0]


    def get_config(self):
        config = {
            'input_dim': self.input_dim,
            'output_dim': self.output_dim,
            'embeddings_initializer':
                initializers.serialize(self.embeddings_initializer),
        }
        base_config = super(RelativePositionEmbedding, self).get_config()
        return dict(list(base_config.items()) + list(config.items()))

总结及反思

本篇从理论到实践介绍了Transformer中的位置编码。首先介绍了位置编码的作用以及主要实现方式；然后重点介绍了主流的位置编码方式，包括训练式位置编码、三角函数式位置编码和相对位置编码，同时基于开源项目bert4keras源码实践了各种位置编码。对Transformer中位置编码的知识和源码实践感兴趣的小伙伴可以多交流。

参考文献

【1】苏剑林. (Dec. 04, 2020). 《层次分解位置编码，让BERT可以处理超长文本》[Blog post]. Retrieved from https://www.kexue.fm/archives/7947

【2】Transformer Architecture: The Positional Encoding, https://kazemnejad.com/blog/transformer_architecture_positional_encoding/

【3】苏剑林. (Feb. 03, 2021). 《让研究人员绞尽脑汁的Transformer位置编码》[Blog post]. Retrieved from https://www.kexue.fm/archives/8130

最新最全的文章请关注我的微信公众号或者知乎专栏：数据拾光者。

码字不易，欢迎小伙伴们点赞和分享。

[人工智能]广告行业中那些趣事系列57：从理论到实战一网打尽Transformer中的位置编码