[人工智能]（NIPS-2018）ChannelNets：通过 Channel-Wise Convolutions 的紧凑而高效的卷积神经网络

ChannelNets：通过 Channel-Wise Convolutions 的紧凑而高效的卷积神经网络

paper题目：ChannelNets: Compact and Efficient Convolutional Neural Networks via Channel-Wise Convolutions

paper发表在NIPS 2018

paper地址：链接

Abstract

卷积神经网络 (CNN) 已显示出解决各种人工智能任务的强大能力。然而，不断增加的模型大小给在资源有限的应用程序中使用它们带来了挑战。在这项工作中，我们建议通过使用通道卷积来压缩深度模型，它用 CNN 中的稀疏连接替换特征映射之间的密集连接。基于这种新颖的操作，我们构建了称为 ChannelNets 的轻量级 CNN。 ChannelNets 使用三个通道卷积实例；即分组通道卷积、深度可分离通道卷积和卷积分类层。与之前为移动设备设计的 CNN 相比，ChannelNet 在不损失精度的情况下，显着减少了参数数量和计算成本。值得注意的是，我们的工作代表了第一次尝试压缩全连接分类层，它通常占紧凑型 CNN 总参数的 25% 左右。 ImageNet 数据集上的实验结果表明，与之前的方法相比，ChannelNets 始终获得更好的性能。

1 Introduction

卷积神经网络 (CNN) 已经展示了解决视觉识别任务的强大能力。自从 AlexNet [11] 在 ImageNet Challenge [3] 上取得了显着的成功之后，各种更深、更复杂的网络 [19, 21, 5] 被提出来创造性能记录。然而，更高的精度通常伴随着越来越多的参数和计算成本。例如，VGG16 [19] 有 1.28 亿个参数，需要 153 亿次浮点运算 (FLOP) 来对图像进行分类。在许多现实世界的应用中，需要在传感器和手机等资源有限的平台上执行预测，因此需要具有更高速度的紧凑模型。模型压缩旨在探索准确性和效率之间的权衡。

最近，模型压缩领域取得了重大进展[7,15,23,6,24]。构建紧凑高效的 CNN 的策略可以分为两类：这些是压缩预训练的网络或设计从头开始训练的新紧凑架构。前一类的研究主要基于传统的压缩技术，如乘积量化 [23]、剪枝 [17]、散列 [1]、霍夫曼编码 [4] 和分解 [12, 9]。

第二类在模型压缩之前已经探索过了。受 Network-In-Network 架构 [14] 的启发，GoogLeNet [21] 引入 Inception 模块来构建更深的网络，而不会增加模型大小和计算成本。通过分解卷积，Inception 模块被 [22] 进一步改进。 [18]中提出的depth-wise separable convolution，推广了分解的思想，并将卷积分解为depth-wise convolution和一个1×1的卷积。该操作已被证明能够以更少的参数实现具有竞争力的结果。在模型压缩方面，MobileNets [6] 和 ShuffleNets [24] 通过采用深度可分离卷积为移动设备设计了 CNN。

在这项工作中，我们专注于第二类并构建了一个新的轻量级 CNN 网络，称为 ChannelNets。通过观察全连接模式占 CNN 中的大多数参数，我们提出了通道卷积，用于用稀疏连接替换特征映射之间的密集连接。像 LeNet-5 [13] 这样的早期工作表明，稀疏连接的网络在资源有限的情况下运行良好。为了在模型压缩中应用通道卷积，我们开发了分组通道卷积、深度可分离通道卷积和卷积分类层。它们用于压缩 CNN 的不同部分，形成我们的 ChannelNet。正如 ImageNet ILSVRC 2012 数据集上的实验结果所示，ChannelNet 在效率和准确性之间取得了比之前的紧凑型 CNN 更好的权衡。值得注意的是，ChannelNets 是第一个尝试压缩全连接分类层的模型，它占紧凑型 CNN 中总参数的 25% 左右。

2 Background and Motivations

CNN 的可训练层通常由卷积层和全连接层组成。大多数先前的研究，如 MobileNets [6] 和 ShuffleNets [24]，都集中在压缩卷积层，其中大部分参数和计算都在其中。为了使讨论具体化，假设二维卷积操作以空间大小为$d_f\times d_f$的$m$个特征图作为输入，并输出$n$个具有相同空间大小且具有适当填充的特征图。$m$和$n$也分别称为输入和输出通道的数量。卷积核大小为$d_k\times d_k$，步幅设置为 1。这里，不失一般性，为简单起见，我们使用方形特征图和卷积核。我们进一步假设卷积运算中没有偏置项，因为现代CNN在卷积后采用了带有偏置的批量归一化[8]。在这种情况下，卷积中的参数数量为$d_k\times d_k\times m\times n$，而 FLOPs 的计算成本为$d_k\times d_k\times m\times n\times d_f\times d_f$。由于每个空间位置共享卷积核，因此对于任何一对输入和输出特征图，连接都是稀疏的，并且由$d_k\times d_k$共享参数加权。然而，通道之间的连接遵循全连接模式，即所有$m$个输入通道都连接到所有$n$个输出通道，因此有$m\times n$项。对于深层卷积层，$m$和$n$通常是像 512 和 1024 这样的大数，因此$m$和$n$通常非常大。

基于上述见解，减少卷积大小和成本的一种方法是规避$d_k\times d_k$和$m\times n$之间的乘法。MobileNets[6]应用这种方法探索了移动设备的紧凑的深度模型。MobileNets采用的核心操作是深度可分离卷积[2]，由深度卷积和$1\times 1$卷积组成，如图1(a)所示。深度卷积对每个输入特征图单独应用一个卷积核，从而产生相同数量的输出通道。使用下面的$1\times 1$卷积，将所有输出通道的信息用一个线性组合进行融合。深度可分离卷积实际上是将常规卷积分解为深度卷积步骤和通道融合步骤。通过这种分解，参数的数量变为
$$d_k\times d_k\times m+m\times n(1)$$
计算成本变成
$$d_k\times d_k\times m\times d_f\times d_f+m\times n\times d_f\times d_f.(2)$$
在两个公式中，第一项对应深度卷积，第二项对应$1\times 1$卷积。通过对$d_k\times d_k$和$m\times n$进行解耦，减少了参数量和计算量。

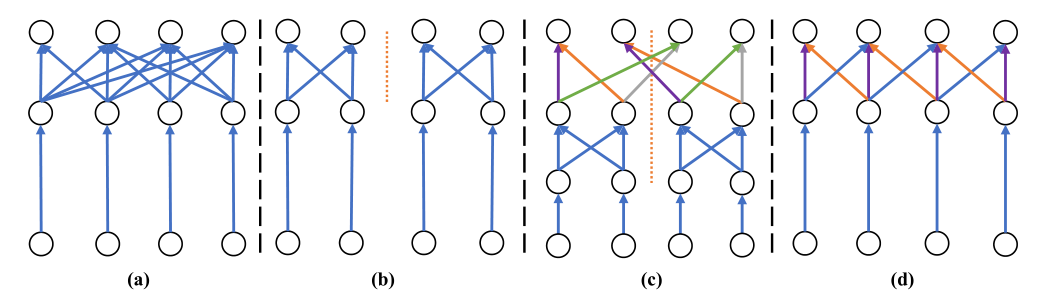
图 1：不同紧凑卷积的图示。 (a)部分展示了depth-wise separable convolution，它由一个depth-wise convolution和一个1×1的卷积组成。 (b) 部分显示了将$1\times 1$卷积替换为$1\times 1$组卷积的情况。 ? 部分说明了使用所提出的组通道卷积进行信息融合。 (d) 部分展示了所提出的深度可分离通道卷积，它由深度卷积和通道卷积组成。对于 ? 和 (d) 中的通道卷积，相同的颜色代表共享权重。

虽然 MobileNets 成功地使用深度可分离卷积来执行模型压缩并获得有竞争力的结果，但值得注意的是，$m\times n$项仍然主导着模型中的参数数量。正如 [6] 中所指出的，导致$m\times n$项的$1\times 1$卷积占 MobileNets 中总参数的 74.59%。对正则卷积的分析表明，$m\times n$来自全连接模式，在$1\times 1$卷积中也是如此。为了理解这一点，首先考虑$d_f=1$的特殊情况。现在输入是$m$个单位，因为每个特征图只有一个单位。由于卷积核大小为$1\times 1$，不会改变特征图的空间大小，因此输出也是$n$个单位。很明显，$m$个输入单元和$n$个输出单元之间的运算是一个$m\times n$参数的全连接运算。当$d_f>1$时，每个空间位置共享全连接操作，因为$1\times 1$卷积。因此，$1\times 1$卷积实际上输出了输入特征图的线性组合。更重要的是，在输入和输出通道之间的连接方面，常规卷积和深度可分离卷积都遵循全连接模式。

因此，压缩卷积的一个更好的策略是改变输入和输出通道之间的密集连接模式。基于深度可分离卷积，它相当于规避了$1\times 1$卷积。以前在AlexNet[11]中使用的一个简单方法是分组卷积。具体来说，m个输入通道被分为$g$个互不相干的组。每个组独立地进行$1\times 1$卷积，产生$n/g$个输出特征图。由于每组的$1\times 1$卷积需要$1/g^2$的参数和FLOPs，与原始的$1\times 1$卷积相比，分组后的总量只有$1/g$。图1(b)描述了一个$1\times 1$组的卷积，其中组的数量为2。

然而，分组操作通常会影响性能，因为各组之间没有互动。因此，不同组中的特征图的信息没有被结合起来，而原始的$1\times 1$卷积则结合了所有输入通道的信息。为了解决这个问题，ShuffleNet[24]被提出，在$1\times 1$组卷积之后，采用了一个混洗层。通过随机排列，混洗层部分地实现了组间的相互作用。但任何输出组都只访问$m/g$输入特征图，因此收集了部分信息。由于这个原因，ShuffleNet不得不采用比MobileNets更深的架构，以达到有竞争力的结果。

3 Channel-Wise Convolutions and ChannelNets

在这项工作中，我们在第 3.1 节中提出了基于通道的卷积，我们在此基础上构建了我们的 ChannelNets。在第 3.2 节中，我们应用分组通道卷积来解决分组引起的信息不一致问题。之后，我们在第 3.3 节中概括了我们的方法，这可以在更深层中直接替换深度可分离卷积。通过对泛化方法的分析，我们提出了一个卷积分类层来代替3.4节中的全连接输出层，进一步减少了参数和计算量。最后，第 3.5 节介绍了我们的 ChannelNets 的架构。

3.1 Channel-Wise Convolutions

我们从一般的通道卷积的定义开始。如上所述，$1\times 1$卷积相当于使用共享的全连接操作扫描输入特征图的每个$d_f\times d_f$位置。通道卷积采用共享的一维卷积操作，而不是全连接操作。因此，输入和输出通道之间的连接模式变得稀疏，其中每个输出特征图都连接到输入特征图的一部分。具体来说，我们再次从$d_f=1$的特殊情况开始。$m$个输入单元（特征图）可以被视为大小为$m$的一维特征图。类似地，输出变成大小为$n$的一维特征图。请注意，输入和输出都只有 1 个通道。通道卷积使用适当的填充执行一维卷积，以将$m$个单元映射到$n$个单元。在$d_f>1$的情况下，为每个空间位置计算相同的一维卷积。因此，内核大小为$d_c$的通道卷积中的参数数量仅为$d_c$，计算成本为$d_c\times n\times d_f\times d_f$。通过使用稀疏连接，我们避免了$m\times n$项。因此，通道卷积消耗的计算量可以忽略不计，并且可以有效地执行。

3.2 Group Channel-Wise Convolutions

我们应用通道卷积来解决分组引起的信息不一致问题。在$1\times 1$组卷积之后，输出是$g$个组，每个组包含$n/g$个特征图。如图 1(b) 所示，$g$组是独立于完全独立的输入特征图组计算的。为了实现组间的交互，在$1\times 1$组卷积之后需要一个有效的信息融合层。融合层有望保留后续组卷积的分组，同时允许每个组从所有组中收集信息。具体来说，这一层的输入和输出都应该是$n$个特征图，分为$g$个组。同时，任何组中的$n/g$个输出通道都应该从所有$n$个输入通道中计算出来。更重要的是，层必须紧凑高效；否则会损害分组的优势。

基于通道卷积，我们提出了组通道卷积，它优雅地用作融合层。给定$n$个分为$g$个组的输入特征图，该操作执行$g$个独立的通道卷积。每个通道卷积使用$g$的步幅并输出具有适当填充的$n/g$特征图。请注意，为了确保所有$n$个输入通道都参与到任何输出通道组的计算中，通道卷积的内核大小需要满足$d_c\ge g$。融合层的期望输出是通过连接这些通道卷积的输出来获得的。图 1? 提供了一个在$1\times 1$组卷积之后使用组通道卷积的示例，它取代了原来的$1\times 1$卷积。

看这个方法的效率，$1\times 1$组卷积后跟组channel-wise卷积的参数个数是$\frac{m}{g}\times \frac{n}{g}\times g+d_c\times g$，计算成本是$\frac{m}{g}\times \frac{n}{g}\times d_f\times d_f\times g+d_c\times \frac{n}{g}\times d_f\times d_f\times g$。由于在大多数情况下，我们的$d_c?m$，与等式 1 和 2 中的第二项相比，我们的方法需要大约$1/g$的训练参数和 FLOP。

3.3 Depth-Wise Separable Channel-Wise Convolutions

基于以上描述，值得注意的是，存在组数与输入输出通道数相等的特殊情况，即$g=m=n$。类似的情况导致了深度卷积的发展[6, 2]。在这种情况下，每个组中只有一个特征图。$1\times 1$组卷积只是简单地缩放深度卷积中的卷积核。由于每层中的批量归一化 [8] 已经涉及缩放项，因此 $1\times 1$组卷积变得多余并且可以被移除。同时，我们没有使用步长为$m$的$m$个独立通道卷积作为融合层，而是应用步长为 1 的单个通道卷积。由于去除了$1\times 1$组卷积，通道-wise的卷积直接跟随深度卷积，产生深度可分离的通道卷积，如图1（d）所示。

本质上，depth-wise separable channel-wise convolution 将depth-wise separable convolution 中的$1\times 1$卷积替换为channel-wise convolution。通道之间的连接直接从密集模式变为稀疏模式。因此，参数数量为$d_k\times d_k\times m+d_c$，成本为$d_k\times d_k\times m\times d_f\times d_f+d_c\times n\times d_f\times d_f$，极大地节省了参数和计算量。该层可用于直接替换深度可分离卷积。

3.4 Convolutional Classification Layer

大多数先前的模型压缩方法很少关注 CNN 的最后一层，这是一个用于生成分类结果的全连接层。以 ImageNet 数据集上的 MobileNets 为例，该层使用 1, 024 个分量的特征向量作为输入，产生 1, 000 个 logits 对应 1, 000 个类。因此，参数数量为 1, 024 × 1, 000 ≈ 100 万，占 [6] 中报告的总参数的 24.33%。在本节中，我们将探索第 3.3 节中提出的深度可分离通道卷积的特殊应用，以减少分类层中的大量参数。

我们注意到倒数第二层通常是全局平均池化层，它将特征图的空间大小减小到 1。例如，在 MobileNets 中，全局平均池化层变换$1,0247\times 7$输入特征映射为$1,0241\times 1$输出特征映射，对应于输入分类层的 1, 024 分量特征向量。一般来说，假设输入特征图的空间大小为$d_f\times d_f$。全局平均池化层相当于一个特殊的深度卷积，内核大小为$d_f\times d_f$，其中内核中的权重固定为$1/d_f^2$。同时，下面的全连接层可以被认为是一个$1\times 1$的卷积，因为输入特征向量可以被看作是$1\times 1$的特征图。因此，全连接分类层之后的全局平均池化层是一个特殊的深度卷积，然后是一个$1\times 1$卷积，从而产生一个特殊的深度可分离卷积。

由于提出的深度可分离通道卷积可以直接替换深度可分离卷积，我们尝试在此处应用替换。具体来说，使用了相同的特殊深度卷积，但后面是一个内核大小为$d_c$的通道卷积，其输出通道的数量等于类的数量。然而，我们观察到这样的操作可以使用常规的 3-D 卷积 [10] 进一步组合。

特别是，$m{d}_f\times d_f$输入特征图可以看作是一个大小为$d_f\times d_f\times m$的单个 3-D 特征图。特殊的深度卷积，或等效的全局平均池化层，本质上是一个内核大小为$d_f\times d_f\times 1$的 3-D 卷积，其中内核中的权重固定为$1/d_f^2$。此外，在这个视角中，通道卷积是一个 3-D 卷积，内核大小为$1\times 1\times d_c$。这两个连续的 3-D 卷积遵循分解模式。如 [22] 中提出的，$d_k\times d_k$卷积可以分解为两个连续的卷积，内核大小分别为$d_k\times 1$和$1\times d_k$。基于这种分解，我们将两个 3-D 卷积组合成一个内核大小为$d_f\times d_f\times d_c$的卷积。假设有$n$个类，为确保输出通道数等于类数，$d_c$设置为$(m?n+1)$，输入上没有填充。该 3-D 卷积用于替换全局平均池化层，然后是全连接层，用作卷积分类层。

虽然卷积分类层显着减少了参数的数量，但人们担心它可能会导致性能的显著损失。在全连接分类层中，每个预测都是基于整个特征向量，考虑到所有特征。相比之下，在卷积分类层中，每个类别的预测仅使用$(m?n+1)$个特征。然而，我们的实验表明，全连接分类层的权重矩阵非常稀疏，表明只有少数特征对类的预测有贡献。同时，我们的具有卷积分类层的 ChannelNets 比具有相似参数数量的其他模型取得了更好的结果。

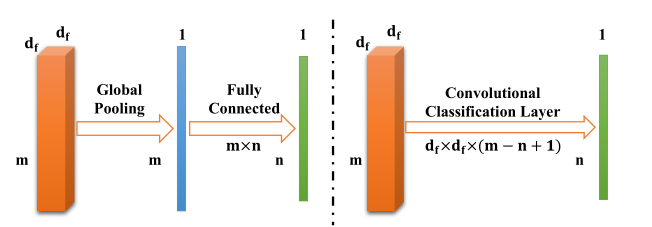
图 2：卷积分类层的图示。左侧部分描述了原始输出层，即全局平均池化层和全连接分类层。全局池化层将空间大小$d_f\times d_f$减小到$1\times 1$，同时保持通道数。然后全连接分类层将通道数从$m$变为$n$，其中$n$是类数。右侧部分说明了所提出的卷积分类层，它执行单个 3-D 卷积，内核大小为$d_f\times d_f\times (m?n+1)$并且没有填充。卷积分类层节省了大量的参数和计算量。

3.5 ChannelNets

通过提出的组通道卷积、深度可分离通道卷积和卷积分类层，我们构建了我们的通道网络。我们遵循 MobileNets 的基本架构以允许公平比较并设计三个具有不同压缩级别的 ChannelNets。值得注意的是，我们提出的方法与 MobileNetV2 [16] 的工作是正交的。与 MobileNets 类似，我们可以将我们的方法应用于 MobileNetV2 以进一步减少参数和计算成本。

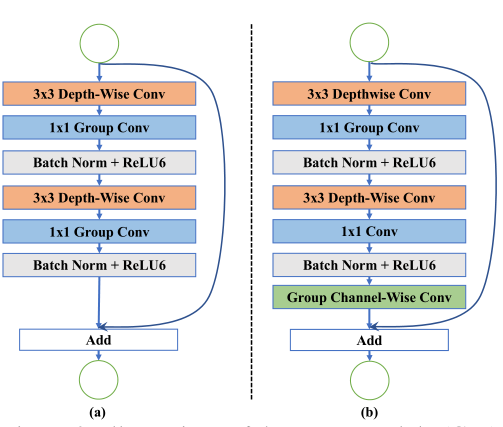
图 3：组模块 (GM) 和组通道模块 (GCWM) 的图示。 (a) 部分显示了 GM，它有两个深度可分离的卷积层。请注意，将$1\times 1$卷积替换为$1\times 1$组卷积以节省计算量。增加了一个skip connection，方便模型训练。 GCWM 在 (b) 部分中进行了描述。与 GM 相比，它具有组通道卷积来融合来自不同组的信息。

ChannelNet-v1：为了使用组通道卷积，我们设计了两个基本模块；它们是组模块（GM）和组通道模块（GCWM）。它们如图 3 所示。GM 仅应用$1\times 1$组卷积而不是$1\times 1$卷积，并添加了一个残差连接 [5]。如上所述，GM 节省了计算量，但存在信息不一致问题。 GCWM 通过在第二个$1\times 1$组卷积之后插入一个组通道卷积来解决这个限制，以实现信息融合。任一模块都可用于替换 MobileNets 中两个连续的深度可分离卷积层。在我们的 ChannelNet-v1 中，我们选择用更大数量的输入和输出通道替换深度可分离卷积。具体来说，具有 512 个输入和输出通道的六个连续的深度可分离卷积层被两个 GCWM 和一个 GM 替换。在这些模块中，我们将组数设置为 2。ChannelNet-v1 中的参数总数约为 370 万。

ChannelNet-v2：我们在 ChannelNet-v1 上应用深度可分离通道卷积来进一步压缩网络。最后一个深度可分离卷积层有 512 个输入通道和 1, 024 个输出通道。我们使用深度可分离通道卷积来替换该层，从而产生 ChannelNet-v2。这种单层替换减少的参数数量为100万，约占ChannelNet-v1中总参数的25%。

ChannelNet-v3：我们在 ChannelNet-v2 上使用卷积分类层来获得 ChannelNet-v3。对于 ImageNet 图像分类任务，类数为 1, 000，即全连接分类层的参数个数为 1024×1000 ≈ 100 万。由于卷积分类层的参数数量只有 7 × 7 × 25 ≈ 1000 个，ChannelNet-v3 大约减少了 100 万个参数。

参考文献