时间序列预测问题
根据输入与输出数量的关系,时间序列预测文题可大致分为:一对一(即单输入单输出),多对一(多输入单输出),多对多(多输入多输出)。
查验数据
本文面对的任务为多对一,即利用股价的相关数据,预测某股开盘价,以交通银行数据为例,数据源自tushare:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tushare as ts
ts.set_token('my token')#个人序列号
pro = ts.pro_api()
data = pro.daily(ts_code='601328.SH')
data如下
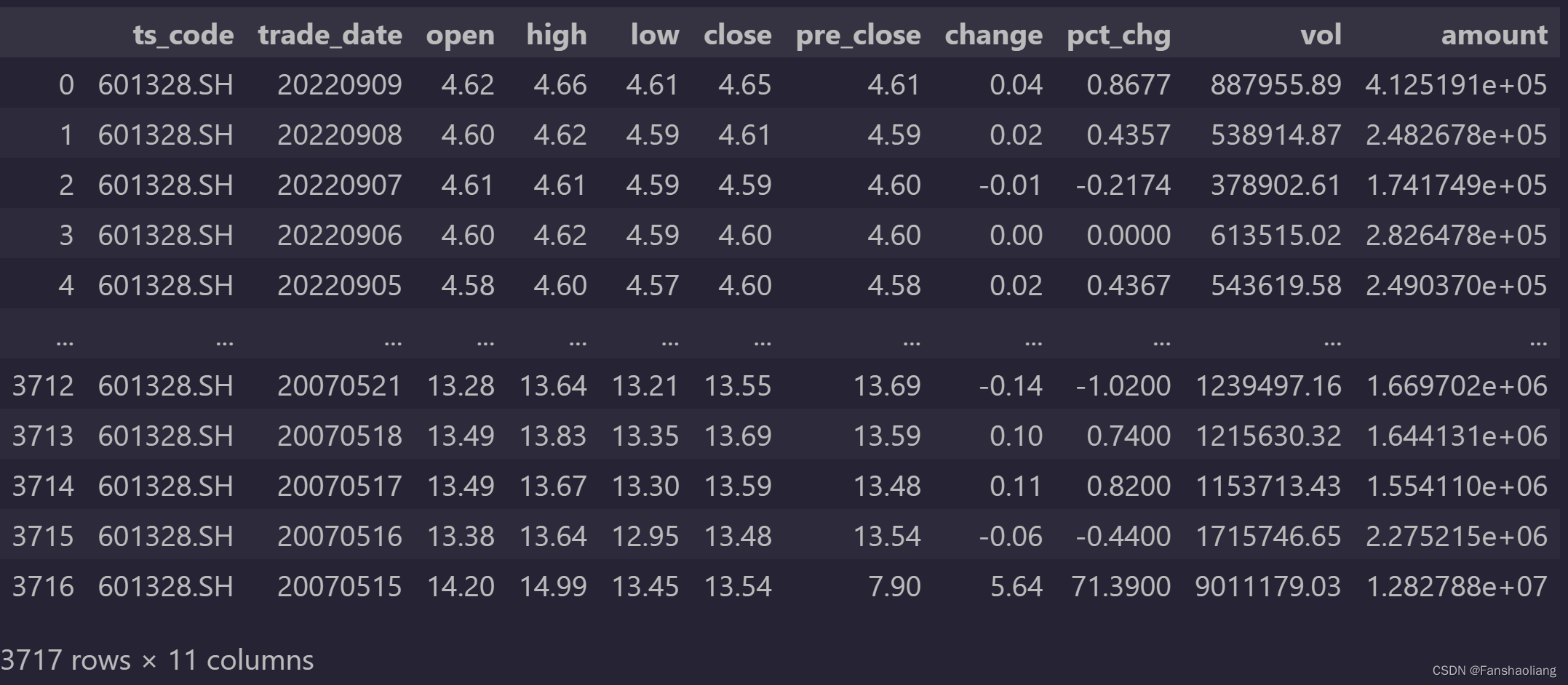
前两列无用,舍弃。查看数据趋势:
cols = list(data1.columns)
fig = plt.figure(figsize=(16,6))
for i in range(len(cols)):
ax = fig.add_subplot(2,5,i+1)
ax.plot(data1.iloc[:,i])
ax.set_title(cols[i])
显示各列趋势为
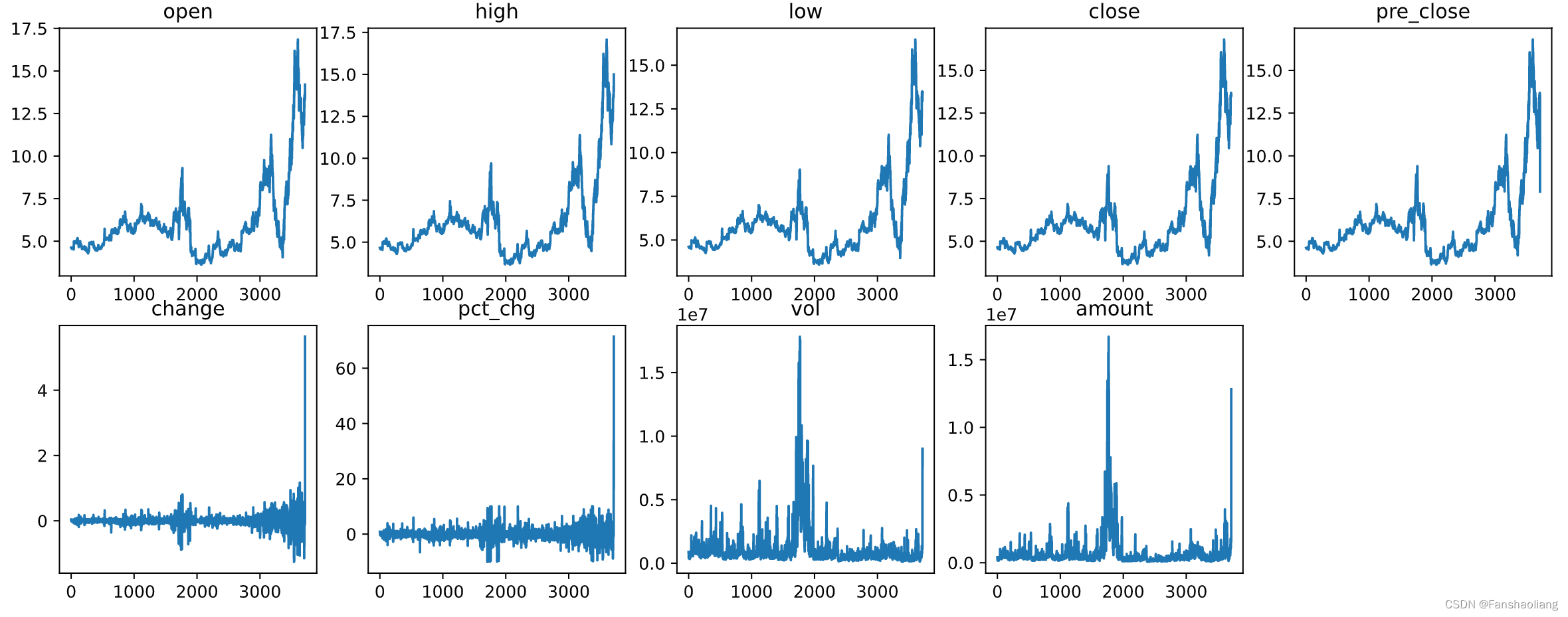
改造数据
接下来改造数据,利用一段时间的数据预测下一时间的值,时间窗口自拟,需要保持一个恰当的长度,本文选择10个点。由于目标为开盘价(open),故第一列为目标,其余列为特征。设计改造函数如下:
def load_data_list_head(data, n_prev = 10):
docX, docY = [], []
for i in range(len(data)-n_prev):
docX.append(data[i:i+n_prev,1:])
docY.append(data[i+n_prev,0])
return np.array(docX), np.array(docY)
为取得较为理想结果,对数据进行归一化,注意量纲差异巨大,所以考虑分开做归一化:
import sklearn
from sklearn.preprocessing import MinMaxScaler as MMS
data = data1.values
scaler_price = MMS(feature_range=(0,1)).fit(data[:,:-4])
scaler_change = MMS(feature_range=(0,1)).fit(data[:,-4].reshape(-1,1))
scaler_pct_change = MMS(feature_range=(0,1)).fit(data[:,-3].reshape(-1,1))
scaler_vol_amount = MMS(feature_range=(0,1)).fit(data[:,-2:])
data_price = scaler_price.transform(data[:,:-4])
data_change = scaler_change.transform(data[:,-4].reshape(-1,1))
data_pct_change = scaler_pct_change.transform(data[:,-3].reshape(-1,1))
data_vol_amount = scaler_vol_amount.transform(data[:,-2:])
指定缩放器scaler后留存,用于生成预测值后反变换回原始量纲。重新捏合数据,指定目标、特征以及划分训练集和测试集:
feature_data = np.c_[
data_price[:,1:],
data_change,
data_pct_change,
data_vol_amount]
target_data = data_price[:,0]
full_data = np.c_[target_data,feature_data]
n_prev = 10#窗口长度10
xx,yy = load_data_list_head(full_data,n_prev)#改造数据
test_size = .25#测试集比例
test_length = round(xx.shape[0]*test_size)#测试集长度
x_train, x_test = xx[:-test_length], xx[-test_length:]
y_train, y_test = yy[:-test_length], yy[-test_length:]
使用TensorFlow中的LSTM
使用tensorflow建模,堆叠模式:
import tensorflow
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dropout, Dense
def build_model():
model = Sequential()# 序列堆叠
model.add(# LSTM层
LSTM(
32,
activation='relu',
input_shape=(x_train.shape[1],x_train.shape[2]))
)
model.add(Dense(1))# 全连接层
model.summary()# 查看模型
return model
model = build_model()
# 损失函数 mse,优化器 adam
model.compile(loss="mse", optimizer="adam")# 编译模型
# 模型训练
history = model.fit(
x_train,
y_train,
batch_size=16,
epochs=32,
validation_split=0.25
)
查看训练过程MSE变化:
plt.figure(figsize=(8,4))
plt.plot(history.history['loss'],label='train loss')
plt.plot(history.history['val_loss'],label='validation loss')
plt.legend()
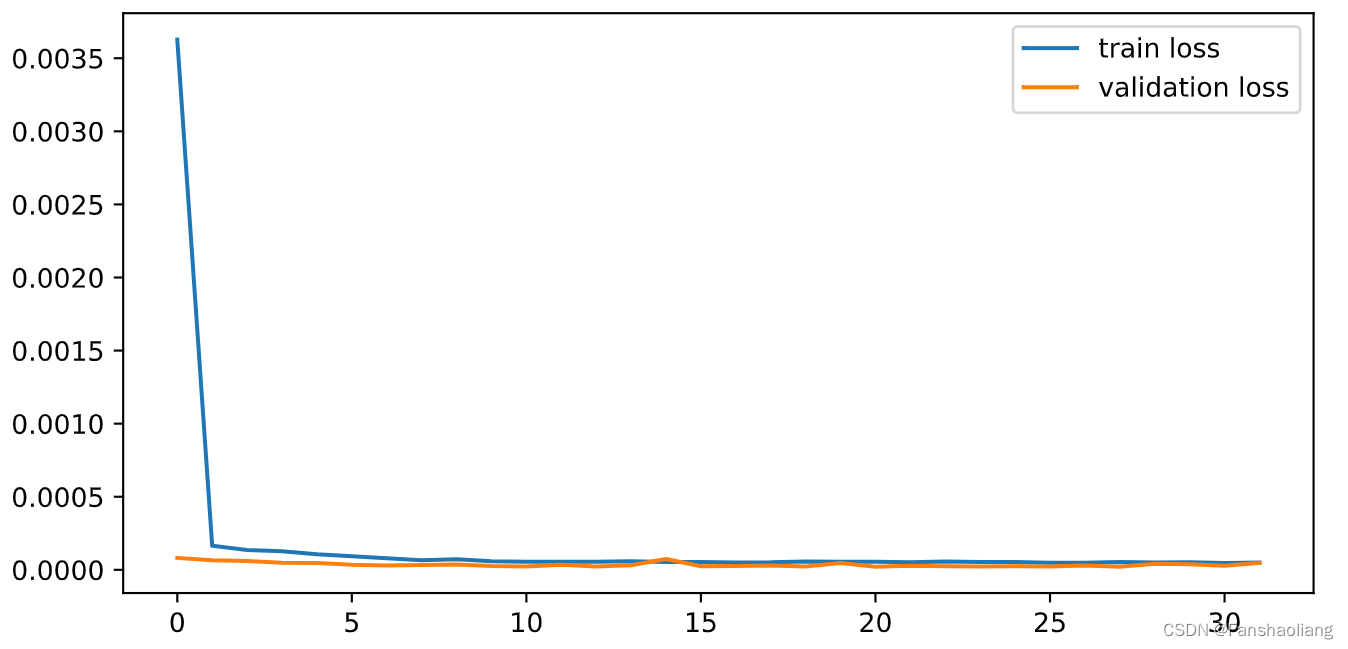
在早期就已收敛,查看预测结果:
y_predict = model.predict(x_test)
plt.figure(figsize=(8,4))
plt.plot(y_predict,label='prediction')
plt.plot(y_test,label='original')
plt.legend()
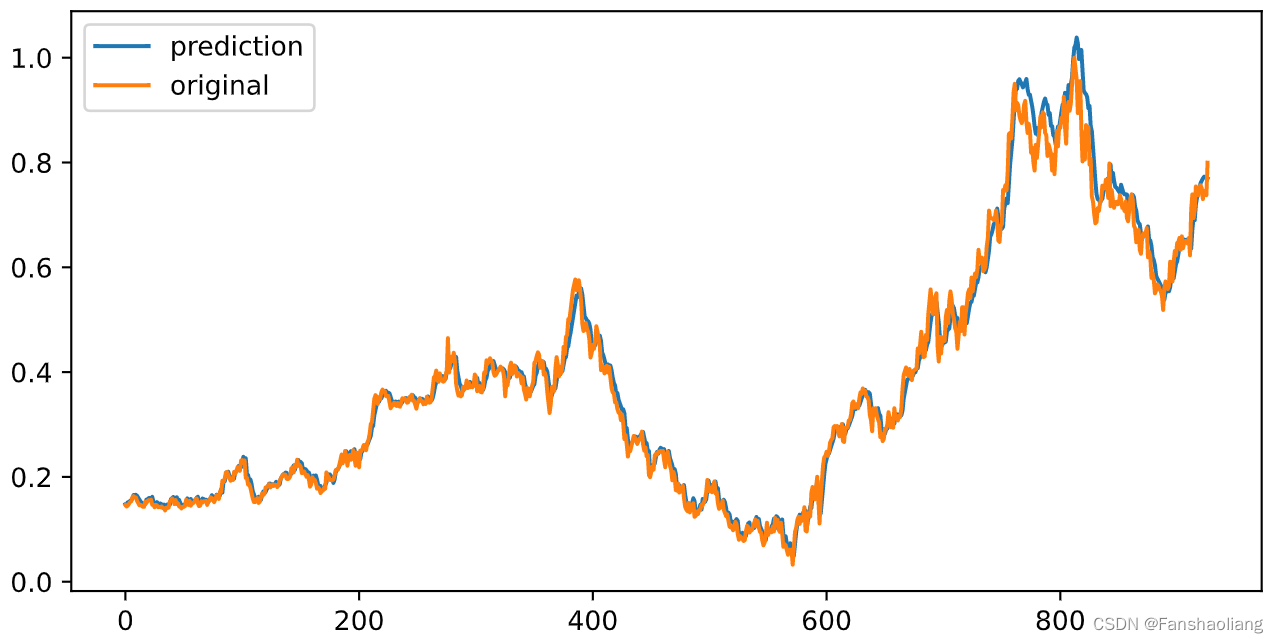
返回原始量纲
差异很小,性质上而言预测成功,但需要返回到原始量纲检验:
inv_y_test = scaler_price.inverse_transform(
np.tile(
np.r_[y_train,y_test],(5,1)
).T
)[-y_test.shape[0]:,0]
inv_y_predict = scaler_price.inverse_transform(
np.tile(
np.r_[y_train,y_predict[:,0]],(5,1)
).T
)[-y_predict.shape[0]:,0]
plt.figure(figsize=(8,4))
plt.plot(inv_y_predict,label='prediction')
plt.plot(inv_y_test,label='original')
plt.title('100 last points')
plt.legend()
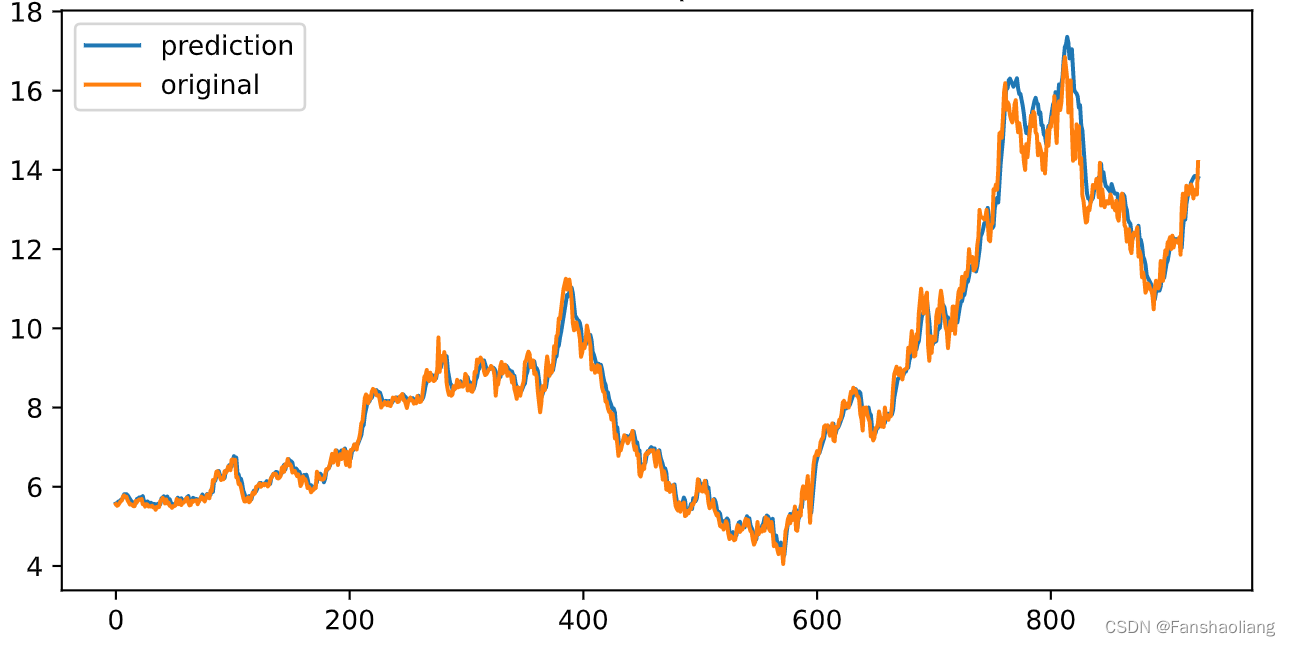
查看最后100个点做最后检验:
plt.figure(figsize=(8,4))
plt.plot(inv_y_predict[-100:],label='prediction')
plt.plot(inv_y_test[-100:],label='original')
plt.title('100 last points')
plt.legend()
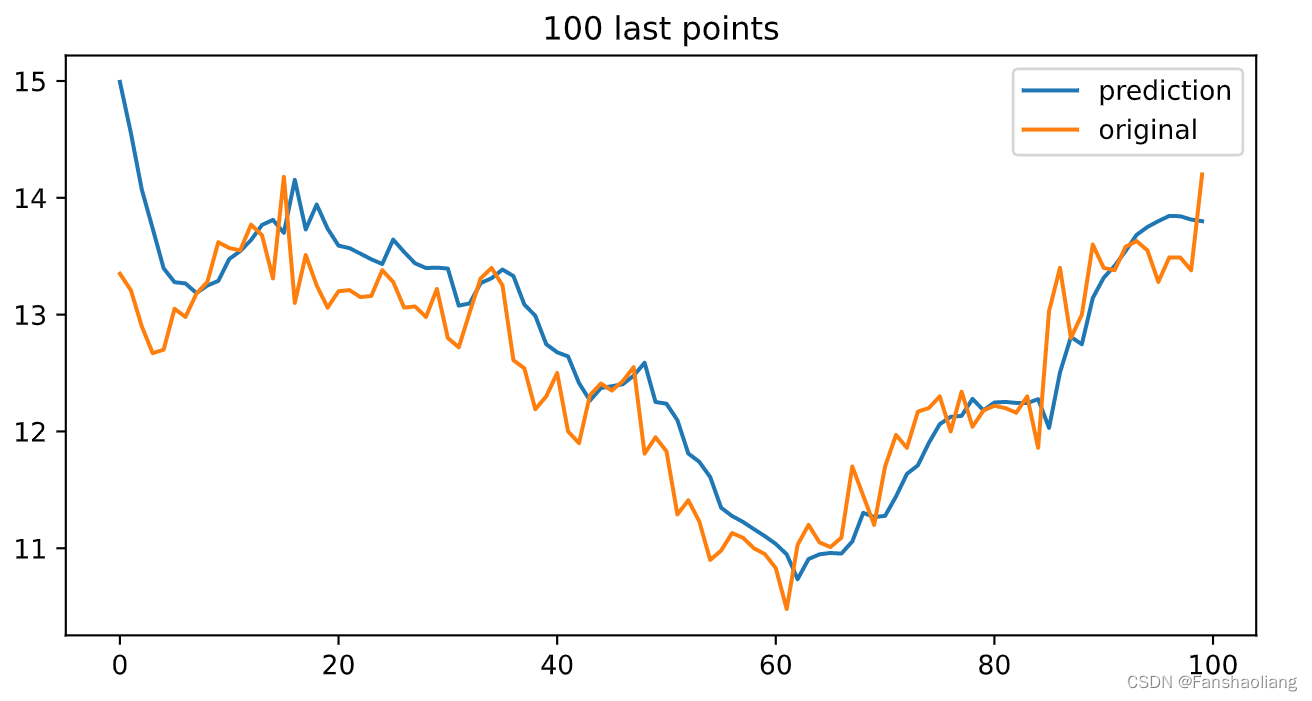
本文关于窗口长度、训练参数、模型参数等未作细致调整,后续可以依托optuna等框架作进一步优化。仅为实验,慎重参考。