这篇看的时候挺早的,那会儿还是arxiv上,这篇发在ICML 2021,其实还是有很有意思的地方的。记录一下大概思路~
这篇整体的思路其实和最开始Uchida 的思路非常一致,主要目的一致,将水印插入在模型参数里面,但并不是随机选择参数,而是小部分更加“重要的”模型参数。
首先是在训练的时候加上一个惩罚项:
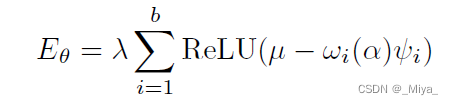
\alpha 表示所有权信息, b是\alpha的大小,\omega 是以所有权信息为输入的符号函数(+,-),\lamda 是调整惩罚项大小的参数,\phi 就是所谓的residual information,其实也可以理解成藏在文章里面的水印。所以现在的关键就两点,一是个人信息,二是水印。
首先是个人信息,插入在\alpha里面,这篇文章的做法使用RSA编码,将一串msg(message)直接和私人密钥加密得到\alpha。
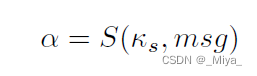
那么编码的符号就是:
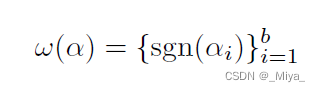
这里sgn将1映射为1,0映射为-1。正常来讲RSA编码出来的应该是一串数字才对,他这里没有说,或者可以是将这串编码完的数字转化为二进制?在Uchida 的文章里面,也是根据正负号训练参数,这篇的做法类似,但是Uchida是根据参数原本的正负号,往两个边界训练参数,这里算是强行限定符号,以符号编码个人信息。
另一部分就是水印,水印其实做法也和Uchida的文章相似,但是前文说到,这里在一些更加重要的参数里面插入标记。所以首先要选出来在哪些参数上插入水印。首先,用以下方程 将第l层的扁平化参数{\omega}^l,转化成 {\gamma} ^l(向量)。有点抽象,但是其实就是将扁平化参数 \omega 拆成了一段一段的,每一段相加并且乘以一个系数(k),这个系数几乎可以近似为这一段的长度(或者近似看成是求这一段的平均值)。
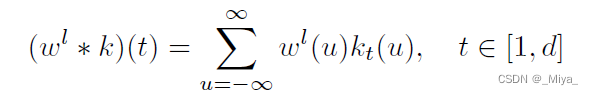
其中,函数k是:
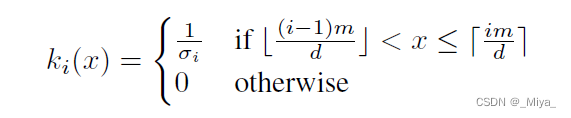
这里面的两个类似中括号的东西分别是floor function 和 ceiling function,其实就是向下和向上取整函数。
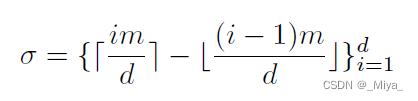
这里的三个式子要注意一下维度,其中m 和d 分别是{\omega}^l 和 {\gamma} ^l 的维度。他这里后面说。m和d 谁大谁小可以任意,但是其实如果m \leq d 的话,\sigmma 就一直等于1,后面两个公式就没什么意义了,这时候相当于给向量\omega 加进去了一些0组成了\gamma。
得到{\gamma}^l 之后,由于\alpha 的大小是b,我们将 \gamma 变成 bb’ 的矩阵,在每一行都取出来绝对值最大的一部分元素(b’\eta(向下取整)个元素,\eta 后面可以选择,文中选了\eta=0.5,也就是百分之五十的元素)组成一个集合\mathcal{B}。最后将第i行组成集合里的元素取平均,就得到了greedy residual(当然在训练过程中这些数是会变的):
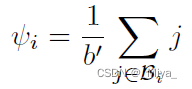
文章在取这些集合\mathcal{B}的时候,因为训练么,所以绝对值最大的是在变化的,每一个batch可能都需要换参数。但是另一方面,文章里面的这个\phi也是有自己的符号的,正常来讲,他们应该同号,这样的话就会往绝对值大的地方跑,符号就是稳定的,但是这里并没有这点保证同号。有意思的是,这就会使得不同号的参数往0跑,同号的变大(也不一定是变大,看\mu的大小,我这里就当作\mu很大,不再细说这一边了)直到选出来同号的为止。也就是他这个算法其实会自然而然地限定选出来的参数的符号。

至于验证部分,首先我们检查模型里面是否存在水印,遵循上面的过程再来一遍就行了!如果有,那么可以用私钥检验一下 所有权的归属。
水印里面的文章有不小一部分都涉及到了密码,但是大部分有个问题就是首先计算量大,其次不是很鲁棒,这篇文章第一点,由于用密码计算的部分比较少,看前面\alpha 是 256,所以计算量对于训练一个正常的神经网络来说是很小的。估计作者也意识到了,所以正文有一部分是在分析计算复杂度,虽然是针对参数提取部分(weight extraction),也就是后面\gamma这一部分。第二点就是不鲁棒,RSA算法还行,不像hash之类的微小改变会整个崩溃。
另一方面,这个方法实际上只在一层里面插入的水印,当然多插几层也不影响,只是收敛可能慢点。其实强行限定符号的行为确实会影响收敛速度,但应该也不是太影响,毕竟只有一层,而且解空间够大。
(ps:今天因为overleaf 崩溃了,所以写的文章,实验部分还没有细看,评价不好说,等看完实验再来补啦~其实这篇是之前一个知友推荐的,上次确实感觉理解的不够,所以这次想想还是把他放上来了。)