[人工智能]9.吴恩达深度学习--机器翻译

本文主要参考了 严宽 大神的深度学习笔记，原文点此进入：吴恩达课后编程作业

一、机器翻译

此模块会构建一个神经机器翻译（NMT）模型，将人类可读日期(“25th of June, 2009”) 翻译为机器可读日期 (“2009-06-25”)。这将会使用到注意力模型（序列模型中最复杂的序列之一）执行此操作。

加载所需要的包：

from keras.layers import Bidirectional, Concatenate, Permute, Dot, Input, LSTM, Multiply
from keras.layers import RepeatVector, Dense, Activation, Lambda
from keras.optimizers import adam_v2
from tensorflow.keras.utils import to_categorical
from keras.models import load_model, Model
import keras.backend as K
import numpy as np

from faker import Faker
import random
from tqdm import tqdm
from babel.dates import format_date
from nmt_utils import *
import matplotlib.pyplot as plt

%matplotlib inline

1. 将人类可读日期翻译成机器可读日期

我们在此构建的模型可用于从一种语言翻译到另一种语言，例如：英语 -> 印地语。但是，语言翻译需要大量数据集，并且通常需要使用 GPU 训练数天。为了让你在不使用大量数据集的情况下尝试使用这些模型，我们将使用更简单的“日期转换”任务。
网络将输入以各种可能格式编写的日期（“the 29th of August 1958”, “03/30/1968”, “24 JUNE 1987”），我们的模型会将它们转换为标准化的机器可读日期（“1958-08-29”, “1968-03-30”, “1987-06-24”）。因此我们将让网络学会以通用的机器可读格式输出日期 “YYYY-MM-DD”。

（1）数据集

我们将在 10000 组人类可读日期以及与之对应的标准化的机器可读日期的数据集上训练模型。运行下面的单元价值数据集并且打印一些样例。

m = 10000
dataset, human_vocab, machine_vocab, inv_machine_vocab = load_dataset(m)

其中：

• dataset：一个元组列表，其格式为：（人类可读日期，机器可读日期）。
• human_vocab：一个字典，将人类可读日期中使用的所有字符映射到整数值索引。
• machine_vocab：一个字典，将机器可读日期中使用的所有字符映射到整数值索引。这些索引不一定与 human_vocab 的索引一致。
• inv_machine_vocab：machine_vocab 的逆字典，从索引到字符的映射。
  打印样例：

dataset[:10]

输出结果如下：

[('tuesday april 6 1993', '1993-04-06'),
 ('22 aug 1997', '1997-08-22'),
 ('23 november 2021', '2021-11-23'),
 ('wednesday october 12 2016', '2016-10-12'),
 ('19.12.03', '2003-12-19'),
 ('june 3 2000', '2000-06-03'),
 ('november 28 2001', '2001-11-28'),
 ('08 may 1992', '1992-05-08'),
 ('september 20 1999', '1999-09-20'),
 ('saturday march 1 2008', '2008-03-01')]

接下来让我们对数据进行预处理，将原始文本数据映射到索引值。
我们使用：Tx=30：假设人类可读日期的最大长度，如果我们得到更长的输入，我们将截断它。Ty=10：因为 “YYYY-MM_DD” 是 10 个字符长度。

Tx = 30
Ty = 10
X, Y, Xoh, Yoh = preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty)

print("X.shape", X.shape)
print("Y.shape", Y.shape)
print("Xoh.shape:", Xoh.shape)
print("Yoh.shape:", Yoh.shape)

输出结果如下：

X.shape: (10000, 30)
Y.shape: (10000, 10)
Xoh.shape: (10000, 30, 37)
Yoh.shape: (10000, 10, 11)

其中：

• X：训练集中人类可读日期的处理版本，其中每个字符都被它在 human_vocab 中映射该字符的索引替换。每个日期都使用特殊字符进一步填充。维度为：X.shape=(m, Tx)
• Y：训练集中机器可读日期的处理版本，其中每个字符都被它在 machine_vocab 中映射的索引替换。维度为：Y.shape=(m, Ty)
• Xoh：X 的 one-hot 版本，one-hot 中条目 “1” 的索引被映射到在 human_vocab 中对应的字符。维度为：Xoh.shape = (m, Tx, len(human_vocab))
• Y0h：Y 的 one-hot 版本，one-hot 中条目 “1” 的索引被映射到由于 machine_vacab 中对应的字符。维度为：Yoh.shape=(m, Tx, len(machine_vocab))。这里 len(machine_vocab)=11因为有 11 个字符（‘-’ 以及 ’0-9‘）。
  让我们看一下预处理训练样本的一些示例。随机选 index 来导航数据集，了解源/目标日期的预处理方式。

index = 0
print("Source date:", dataset[index][0])
print("Target date:", dataset[index][1])
print()
print("Source after preprocessing (indices):", X[index])
print("Target after preprocessing (indices):", Y[index])
print()
print("Source after preprocessing (one-hot):", Xoh[index])
print("Target after preprocessing (one-hot):", Yoh[index])

测试结果如下：

Source date: tuesday april 6 1993
Target date: 1993-04-06

Source after preprocessing (indices): [30 31 17 29 16 13 34  0 13 27 28 21 23  0  9  0  4 12 12  6 36 36 36 36
 36 36 36 36 36 36]
Target after preprocessing (indices): [ 2 10 10  4  0  1  5  0  1  7]

Source after preprocessing (one-hot): [[0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 ...
 [0. 0. 0. ... 0. 0. 1.]
 [0. 0. 0. ... 0. 0. 1.]
 [0. 0. 0. ... 0. 0. 1.]]
Target after preprocessing (one-hot): [[0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]]

2. 带注意力的神经机器翻译

如果你不得不将一本书的段落从法语翻译成英语, 你不会阅读整段，然后合上书并翻译。甚至在翻译过程中, 您将阅读/重新阅读并专注于与您所写的英语部分相对应的法文段落部分。注意机制告诉神经机器翻译模型，它应该在任何一步都要有注意力。

（1）注意力机制

在这部分，你将实现课程中介绍的注意力机制。下图是模型的工作原理图。图1展示了注意力模型，图2展示了一个“注意”步骤：计算注意力变量 ${\alpha }^{<t,t^{\prime }>}$，使用注意力变量计算输出中每个时间步（$\text{t}=1,\dots ,T_{\text{y}}$）的上下文变量 ${\text{context}}^{<t>}$

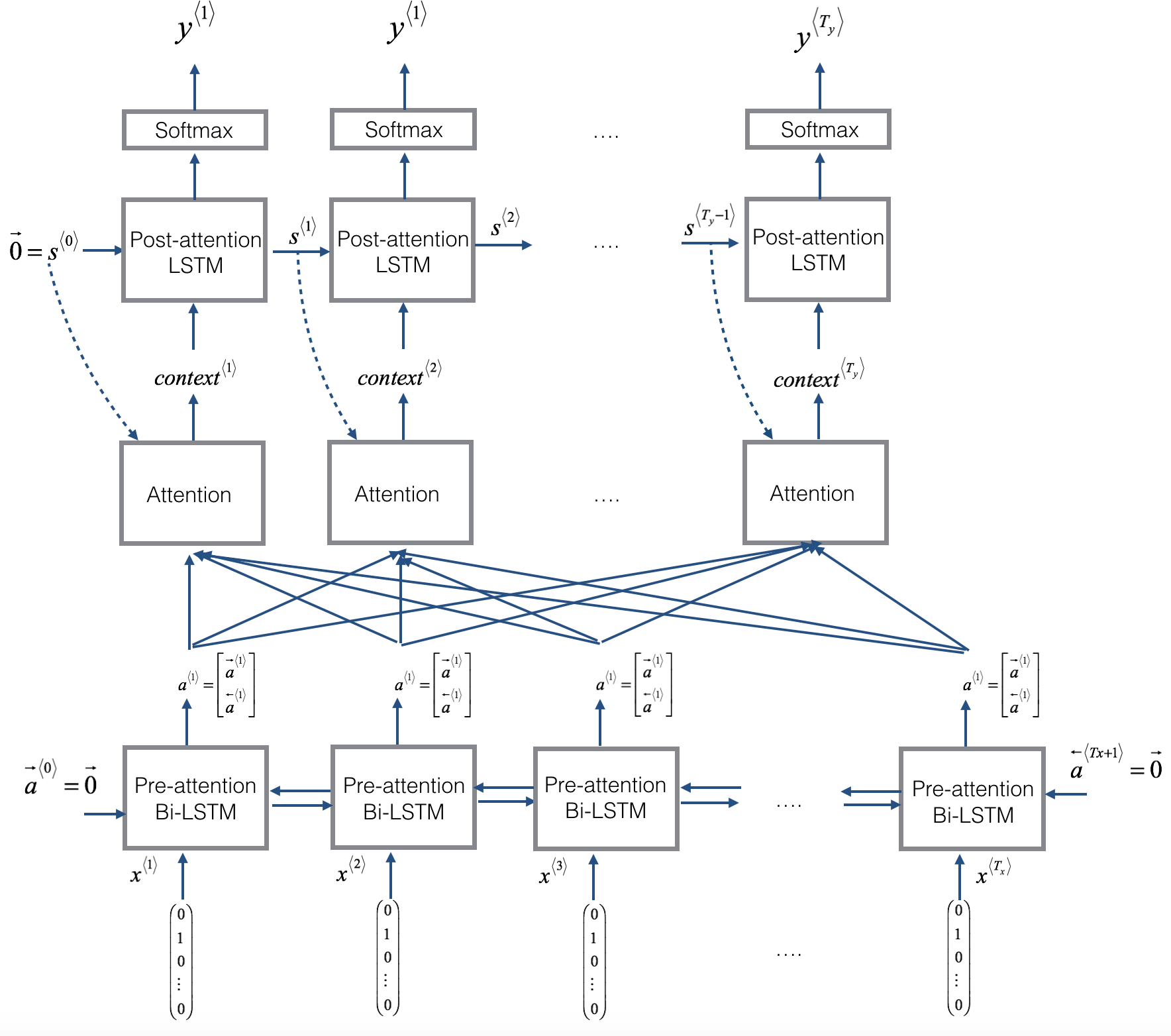
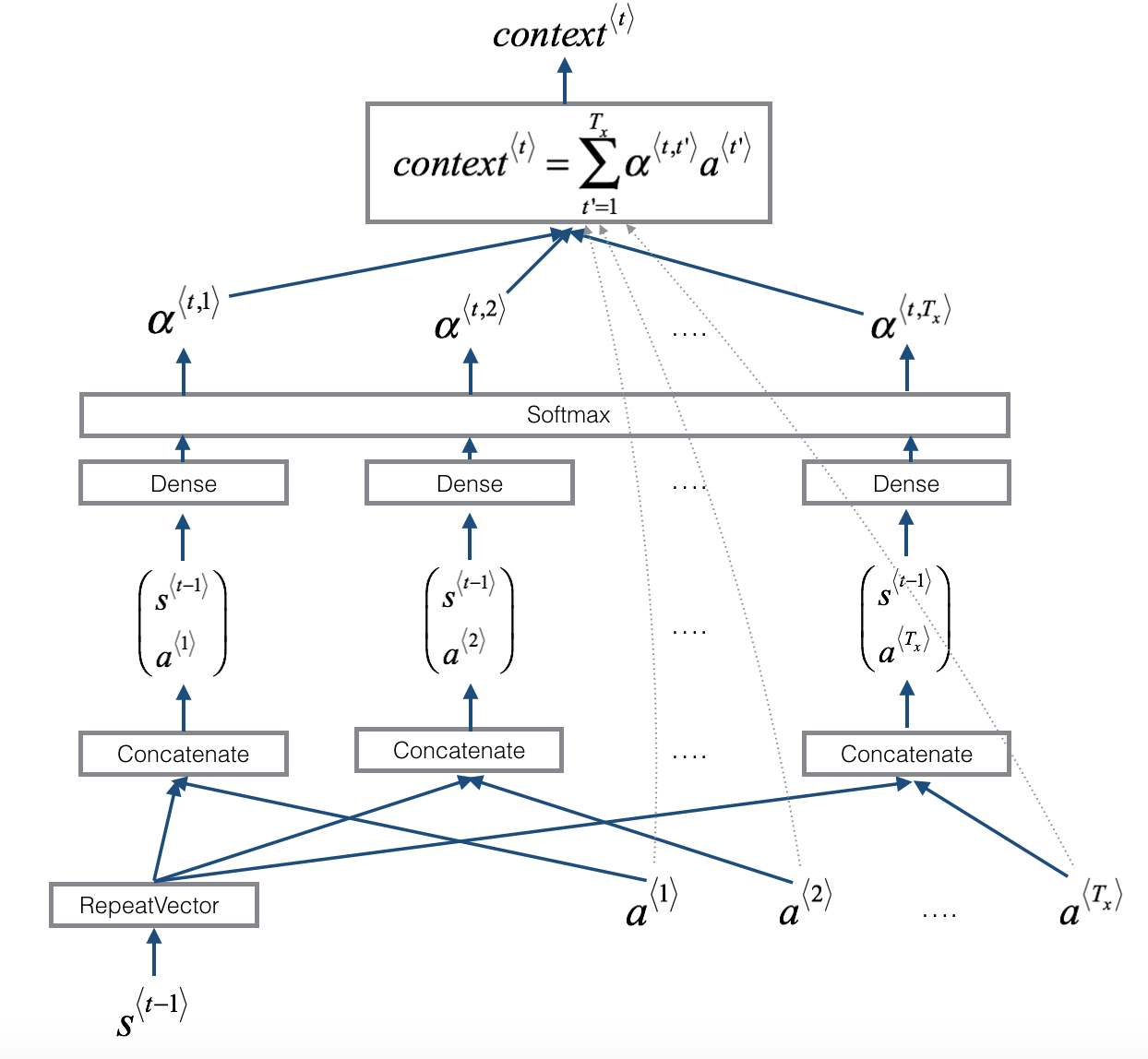
注意：

• 模型中有两种 LSTM。一个是图片底部的 Bi-LSTM（双向LSTM），在 Attention 前，我们叫做 pre-attention Bi-LSTM。另一个是图片顶部在 Attention 后LSTM，我们称为 post-attention LSTM。pre-attention Bi-LSTM 经历 ${\text{T}}_{\text{x}}$ 时间步；post-attention LSTM 经历 ${\text{T}}_{\text{y}}$ 时间步。
• post-attention LSTM 通过 $s^{<t>},c^{<t>}$ 从一个时间步到下一个。对于 post-attention 序列模型我们仅使用了基本的 RNN，状态被 RNN 输出激活捕获 $s^{<t>}$。但是因为我们在这里使用 LSTM，LSTM 有输出激活 $s^{<t>}$ 和隐藏单元状态 $c^{<t>}$。但是，与之前的文本生成示例不同，在此模型中，post-activation LSTM 在时间 $\text{t}$ 不会有具体生成的 ${\text{y}}^{<t?1>}$ 作为输入；只需要 $s^{<t>}$ 和 $c^{<t>}$ 作为输入。我们以这种方式设计了模型，因为（与相邻字符高度相关的语言生成不同）在 YYYY-MM-DD 日期中，前一个字符与下一个字符之间的依赖性不强。
• 我们用 ${\text{a}}^{<t>}=[a^{<t>};]$ 表示 pre-attention Bi-LSTM 的前向和后向激活串联起来
• 下面的图使用了 RepeatVector 节点复制 $s^{<t?1>}$ 的值 ${\text{T}}_{\text{x}}$ 次，然后 Concatenation 串联 $s^{<t?1>}$ 和 $a^{<t>}$ 计算 $e^{<t,t^{\prime }>}$，再通过 softmax 计算 $a^{<t,t^{\prime }>}$。我们将在下面解释如何在 Keras 中使用 RepeatVector 和 Concatenation。

为了实现这个模型，首先我们需要实现如下两个功能：

• one_step_attention()：在步骤 $t$，给出 Bi-LSTM 的所有隐藏状态（$[{\text{a}}^{<1>},{\text{a}}^{<1>},\dots ,{\text{a}}^{<{\text{T}}_{\text{x}}>}]$）以及第二个 LSTM 的先前隐藏状态（$s^{<t?1>}$），one_step_attention() 计算注意力权重（$[{\text{a}}^{<1>},{\text{a}}^{<2>},\dots ,{\text{a}}^{<{\text{T}}_{\text{x}}>}]$）以及第二个 LSTM 的先前隐藏状态（${\text{s}}^{<t?1>}$），one_step_attention() 计算注意力权重（$[{\alpha }^{<t,1>},{\alpha }^{<t,2>},\dots ,{\alpha }^{<t,{\text{T}}_{\text{x}}>}]$）并输出上下文向量：$${\text{context}}^{<t>}=\sum _{t^{\prime }=0}^{{\text{T}}_{\text{x}}}{\alpha }^{<t,t^{\prime }>}{\text{a}}^{<t^{\prime }>}$$请注意，我们在这个 notebook 中用 ${\text{context}}^{<t>}$ 表示注意力。在视频中用 ${\text{c}}^{<t>}$ 表示 $\text{context}$，但在这里我们称之为 ${\text{context}}^{<t>}$，避免与 post-attention LSTM 内部存储器单元变量混淆，它有时也用 ${\text{c}}^{<t>}$ 表示。
• model()：实现整个模型。首先根据输入执行Bi-LSTM 返回 $[{\text{a}}^{<1>},{\text{a}}^{<2>},\dots ,{\text{a}}^{<{\text{T}}_{\text{x}}>}]$。然后，调用 one_step_attention() ${\text{T}}_{\text{y}}$ 次。在这个循环的每次迭代中，将获得上下文向量 ${\text{c}}^{<t>}$ 给第二个 LSTM，根据 LSTM 的输出，运行 softmax 激活的全连接层以生成预测 ${\hat{\text{y}}}^{<t>}$。

接下来实现 one_step_attention()。然后函数 model() 使用 for 循环调用 one_step_attention() 中的层 ${\text{T}}_{\text{y}}$ 次，很重要的一点是所有 ${\text{T}}_{\text{y}}$ 的拷贝有相同权重。也就是说，不应该每次都重新确定权重，即所有 ${\text{T}}_{\text{y}}$ 步骤都共享权重。要想在 Keras 中实现具有可共享权重的层，必须实现以下两个步骤：

1. 定义层对象（作为样本的全局变量）
2. 在传播输入时调用这些对象

我们先将需要的层定义为全局变量：

# 将共享层定义为全局变量 
repeator = RepeatVector(Tx)   # 在轴1方向复制数据
concatenator = Concatenate(axis=-1)
densor1 = Dense(10, activation = "tanh")
densor2 = Dense(1, activation = "relu")
activator = Activation(softmax, name='attention_weights') # 在这个 notebook 我们正在使用自定义的 softmax(axis = 1)
dotor = Dot(axes = 1)   # 计算两个张量中的点乘

现在你可以使用这些图层来实现 one_step_attention()。为了通过这些层来传播 Keras 张量对象 X，可以使用 layer(X)（或 layer([X, Y]），如果它需要多个输入）。例如：densor2(X) 就将通过上面定义的 Dense(1) 层来传播 X。

def one_step_attention(a, s_prev):
    """
    执行一步 attention: 输出一个上下文向量，输出作为注意力权重的点积计算的上下文向量
    "alphas"  Bi-LSTM的 隐藏状态 "a"
    
    参数：
    a --  Bi-LSTM的输出隐藏状态 numpy-array 维度 (m, Tx, 2*n_a)
    s_prev -- (post-attention) LSTM的前一个隐藏状态, numpy-array 维度(m, n_s)
    
    返回：
    context -- 上下文向量, 下一个(post-attetion) LSTM 单元的输入
    """
    
    # 使用 repeator 重复 s_prev 维度 (m, Tx, n_s)  这样你就可以将它与所有隐藏状态 a 连接起来
    s_prev = repeator(s_prev)
    # 使用 concatenator 在最后一个轴上连接 a 和 s_prev
    concat = concatenator([a, s_prev])
    # 使用 densor1 传入参数 concat，通过一个小的全连接神经网络来计算”中间能量“变量e
    e = densor1(concat)
    # 使用 densor2 传入参数 e，通过一个小的全连接神经网络来计算"能量"变量 energies
    energies = densor2(e)
    # 使用 activator 传入参数 energies 计算注意力权重 alphas 
    alphas = activator(energies)
    # 使用 dotor 传入参数 alphas 和 a 计算下一个 (post-attention) LSTM 单元的上下文向量
    context = dotor([alphas, a])
    
    return context

实现 model()函数：

# 定义全局图层用于在 model() 中共享
n_a = 32
n_s = 64
post_activation_LSTM_cell = LSTM(n_s, return_state=True)
output_layer = Dense(len(machine_vocab), activation = softmax)

现在你可以在 for 循环中使用这些图层 ${\text{T}}_{\text{y}}$ 次来生成输出，并且他们的参数不会重新初始化。你必须执行以下步骤：

1. 传入输入参数到 Bi-LSTM
2. 迭代 $\text{for}\text{t}=0,\dots ,{\text{T}}_{\text{y}}?1$：
   • 调用 one_step_attention()，使用 $[{\alpha }^{<t,1>},{\alpha }^{<t,2>},\dots ,{\alpha }^{<t,{\text{T}}_{\text{x}}>}]$ 和 $s^{<t?1>}$ 为参数，获取上下文向量 ${\text{context}}^{<t>}$。
   • 使用 ${\text{context}}^{<t>}$、上一步隐藏状态 $s^{<t?1>}$ 和上一步单元状态 $c^{<t?1>}$ 作为参数给 post-attention LSTM 单元，使用 initial_state = [previous_hidden_state, previous_cell_state]。返回新的隐藏状态 $s^{<t>}$ 和新的单元状态 $c^{<t>}$。
   • 应用 softmax 图层 $s^{<t>}$，获取输出。
   • 通过将输出添加到输出列表来保存输出。
3. 创建 Keras 模型实例。

def model(Tx, Ty, n_a, n_s, human_vocab_size, machine_vocab_size):
    """
    参数:
    Tx -- 输入序列的长度
    Ty -- 输出序列的长度
    n_a -- Bi-LSTM的隐藏状态大小
    n_s -- post-attention LSTM的隐藏状态大小
    human_vocab_size -- python字典 "human_vocab" 的大小
    machine_vocab_size -- python字典 "machine_vocab" 的大小

    返回：
    model -- Keras 模型实例
    """
    
    # 定义模型的输入，维度为 (T_x, )
    # 定义 s0 和 c0，初始化解码器 LSTM 的隐藏状态，维度为 (n_s, )
    X = Input(shape=(Tx, human_vocab_size))
    s0 = Input(shape=(n_s, ), name='s0')
    c0 = Input(shape=(n_s, ), name='c0')
    s = s0
    c = c0
    
    # 初始化一个空的输出列表
    outputs = []
    
    # 1. 定义 pre-attention Bi-LSTM。记得使用 return_sequences=True
    a = Bidirectional(LSTM(n_a, return_sequences=True), input_shape=(m, Tx, n_a * 2))(X)
    
    # 2. 迭代 Ty 步
    for t in range(Ty):
        # (1) 执行一步注意机制，得到在t 步的上下文向量
        context = one_step_attention(a, s)
        
        # (2) 使用post-attention LSTM 单元得到新的 context
        # 别忘了使用：initial_state = [hidden_state, cell_state]
        s, _, c = post_activation_LSTM_cell(context, initial_state=[s, c])
        
        # (3) 使用全连接层处理 post-attention LSTM 的隐藏状态输出
        out = output_layer(s)
        
        # (4) 追加 out 到 outputs 列表
        outputs.append(out)
        
    # 3. 创建模型实例，获取三个输入并返回输出列表
    model = Model(inputs=[X, s0, c0], outputs=outputs)
    
    return model

创建模型，并查看模型的摘要：

model = model(Tx, Ty, n_a, n_s, len(human_vocab), len(machine_vocab))
model.summary()

在 Keras 创建模型后，你需要编译它并定义模型使用的损失、优化和评估指标。编译模型时，损失使用 categorical_crossentropy，优化算法使用 Adam(lr=0.005, beta_1=0.9, beta_2=0.999, decay=0.01)，评估指标使用 ['accuracy']：

opt = adam_v2.Adam(lr = 0.005, beta_1 = 0.9, beta_2 = 0.999, decay = 0.01)
model.compile(loss = 'categorical_crossentropy', optimizer = opt, metrics = ['accuracy'])

最后，定义所有的输入和输出并训练模型：我们已经有包含训练样例的 X，维度（$\text{m}=10000,{\text{T}}_{\text{x}}=30$），你需要创建用 0 初始化的 s0 和 c0，用于初始的 post_activation_LSTM_cell。给定的 model()，你需要“输出”11个维度为（m, Ty）元素的列表，以便 outputs[i][0], ..., outputs[i][Ty] 表示 第 $i$ 个训练样本（X[i]）对应的真是标签（字符）。大多数情况下，第 $i$ 个训练样本中第 $j$ 个字符的真正的标签是 outputs[i][j]。

s0 = np.zeros((m, n_s))
c0 = np.zeros((m, n_s))
outputs = list(Yoh.swapaxes(0,1))

对模型进行训练：

history = model.fit([Xoh, s0, c0], outputs, epochs=100, batch_size=100)

在训练时，你可以看到输出的 10 个位置中的每个位置的损失和准确性。下表给出了一个例子，说明如果每个批次有两个例子，精度可能时多少：

所以，dense_2_acc_8: 0.89 表示在当前批量数据中，89%的时间正确预测输出了第 7 个字符。