翻译距离模型Translation Distance Models

数值化知识

知识图谱（KG）是由实体 (节点) 和关系 (不同类型的边) 组成的多关系图。每条边都表示为形式 (头实体、关系、尾实体) 的三个部分，也称为事实，表示两个实体通过特定的关系连接在一起。虽然在表示结构化数据方面很有效，但是这类三元组的底层符号特性通常使 KGs 很难操作。为了解决这个问题，提出了一种新的研究方向——知识图谱嵌入。关键思想是嵌入 KG 的组件，包括将实体和关系转化为连续的向量空间，从而简化操作，同时保留 KG 的原有的结构。那些实体和关系嵌入能进一步应用于各种任务中，如 KG 补全、关系提取、实体分类和实体解析。

融合事实信息的知识图谱嵌入

步骤：
①使用连续向量空间表示实体关系，关系通常被视为向量空间的运算。
②定义评分函数，用来测量事实的合理性。
③学习实体关系的表示，优化问题：最大化全局观测事实的合理性。

【表示学习】：表示学习旨在将研究对象的语义信息表示为稠密低维实值向量，知识表示学习主要是面向知识图谱中的实体和关系进行表示学习。使用建模方法将实体和关系表示在低维稠密向量空间中，然后进行计算和推理。简单来说，就是将三元组表示成向量的这个过程就称为表示学习

有两个主要分类：

①平移距离模型 translational distance models 前者使用基于距离的评分函数
②语义匹配模型 semantic matching models 后者使用基于相似度的评分函数

trans

平移距离模型利用基于距离的评分函数。通常是在通过关系进行翻译之后，用两个实体之间的距离来衡量一个事实的合理性。

一系列trans实际上是对打分函数的不断更新，其余没有啥创新点

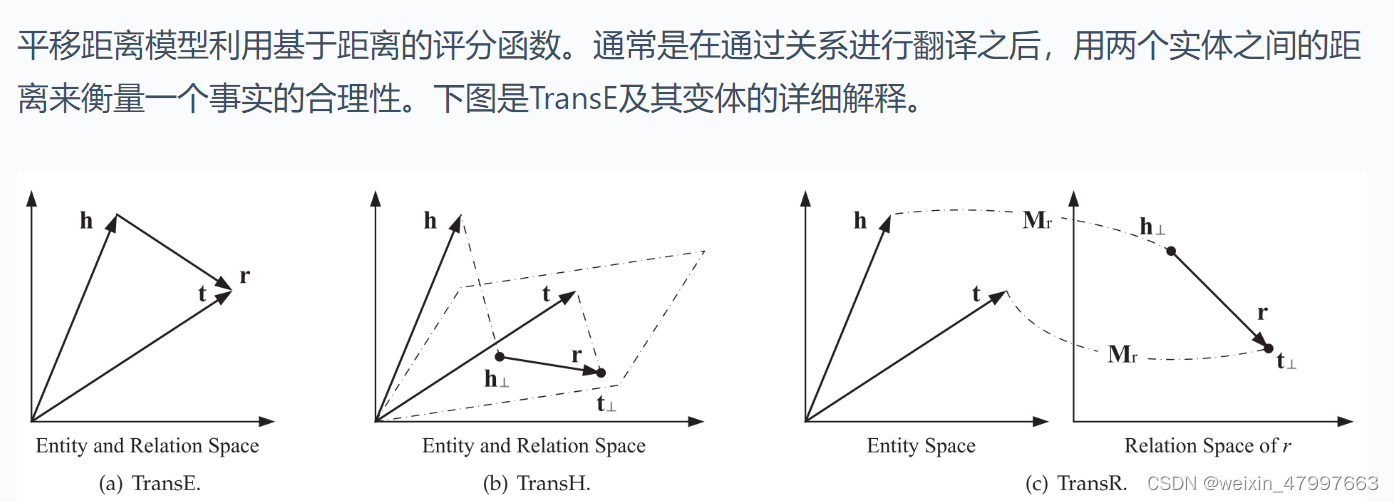
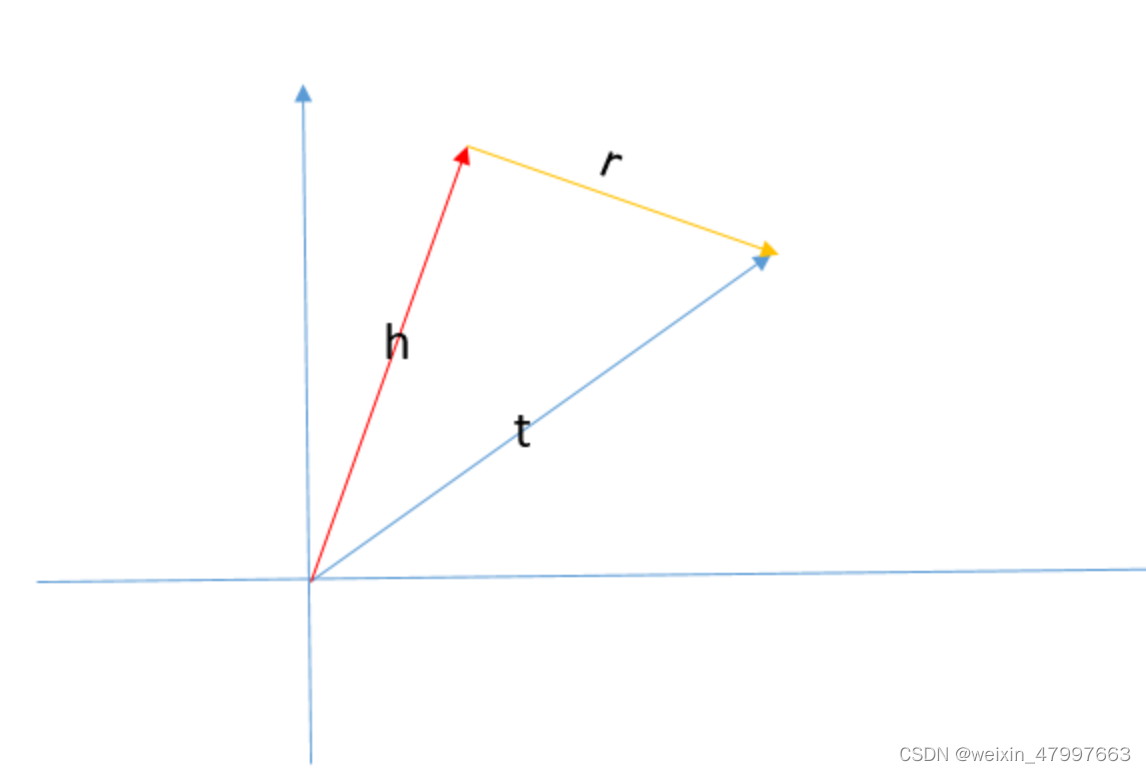
在这里插入图片描述

transE

https://blog.csdn.net/hei653779919/article/details/104278583
https://www.cnblogs.com/chenbjin/p/5644457.html
在这里插入图片描述

在这里插入图片描述

我们使用范数来衡量向量的长度并且衡量向量之间的距离，希望正确的三元组距离差短，错误的三元组距离差长，同时我们的参数gmma是来支撑错误样本的距离，如果gmma越大错误样本之间的距离越大。如果说错误样本的距离足够大，正例距离足够小，那么我们不需要进行loss反向梯度下降
一般我们使用L1/2正则化来避免过拟合
图上的加号是大于0取原值，小于0则为0。我们叫做合页损失函数(hinge loss function)，这种训练方法叫做margin-based ranking criterion。是不是听起来很熟悉？对的，就是来自SVM。支持向量机也是如此，要将正和负尽可能分开，找出最大距离的支持向量。同理，TransE也是如此，我们尽可能将对的和错的分开。margin值一般设为1了。

在这里插入图片描述

def forward(self, data):
        # 前向传播
        h_embedding, r_embedding, t_embedding = self.get_triplet_embedding(data=data)
        h_embedding = F.normalize(h_embedding, p=2, dim=1)
        t_embedding = F.normalize(t_embedding, p=2, dim=1)
        score = F.pairwise_distance(h_embedding + r_embedding, t_embedding, p=self.p_norm)
        return score

def loss(self, data):
        # 计算损失
        pos_data = data
        neg_data = self.model_negative_sampler.create_negative(data)

        
        pos_score = self.forward(pos_data)
        neg_score = self.forward(neg_data)

        return self.model_loss(pos_score, neg_score) + self.penalty(data)

transE是考虑到了word2vec的平移不变性，即 V(king) - V(man) + V(woman) ≈ V(queue)

transH

TransE模型在反射，一对多，多对一等关系中处理的效果并不好，要求发生相似性不高的向量发生位置的相似，这是不好的。
所以transH通过投影的方法解决这一问题，对于不同的关系设置不同的投影超平面。
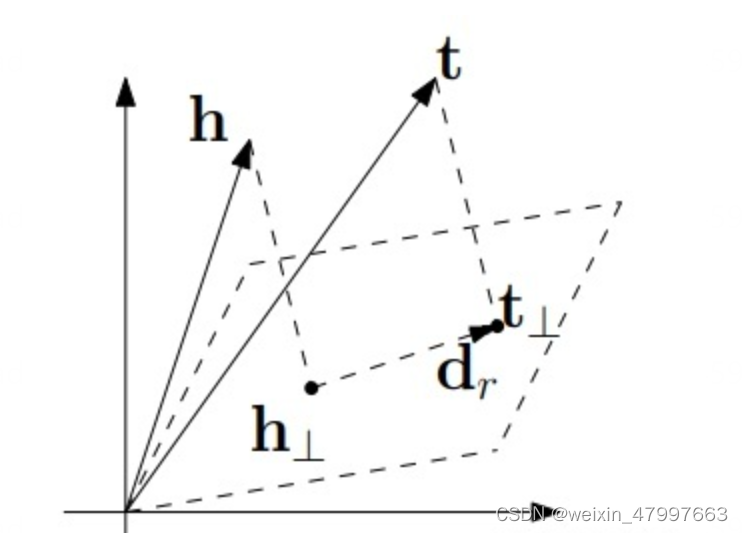
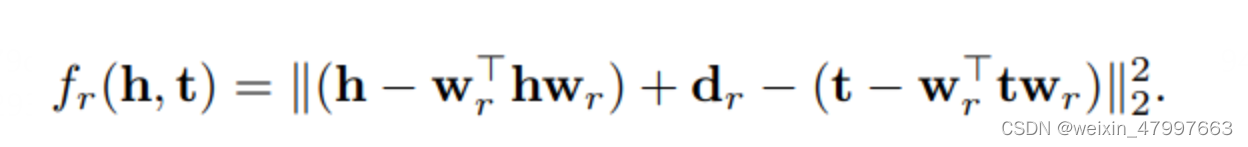
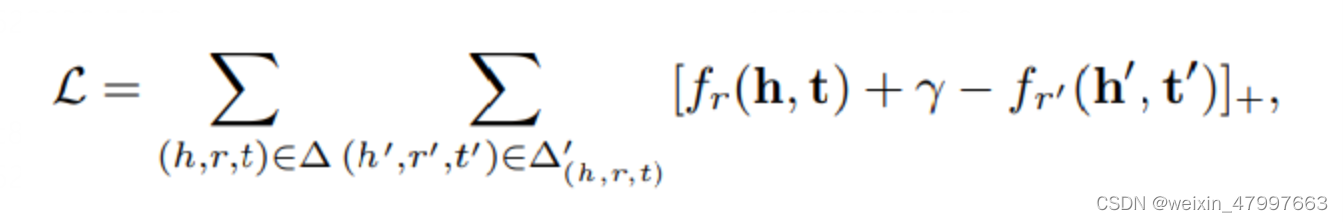
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

文章另一个创新点是提出了新的采样方法 bern。原始的负采样方法是从实体集中随机抽取一个实体替换到 golden triplet 中生成负样本，但是这样做有可能会得到假阳（false negative）的负样本。对于这种情况，文章的解决策略是：对于 1-N 的关系，赋予更高的概率替换头实体，而对于 N-1 的关系，赋予更高的概率替换尾实体。具体地，对每个关系计算其 tph （每个头实体平均对应几个尾实体）和 hpt （每个尾实体平均对应几个头实体）。对于 tphtph+hpt 越大的，说明是一对多的关系，在负采样时替换头实体，更容易获得 true negative。我曾经思考过这个问题，如果在普通的 unif 采样时，加一个检验，看下生成的负样本是否存在于 KG 中，这样是不是就可以避免生成 false negative？但是这样的策略默认遵从了一个假设，即 KG 之外的知识全都是错误的（即封闭世界假定 Closed World Assumption），即使生成的负样本不存在于训练集中，也不代表它就是 negative 的，而一般 KG 训练的时候遵循的是开放世界假定（Open World Assumption, OWA），对于未知的命题不知道正确与否，所以 bern 通过局部推测整体，一对多关系在整个知识体系中也更可能是一对多关系，增大替换头实体的概率确实更易得到 negateive，因此 bern 策略是有意义的。

transR

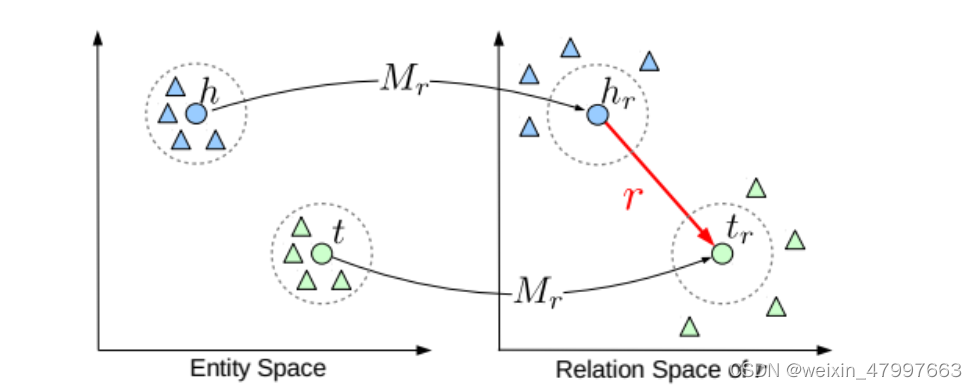
transH不过这两个模型均是假定实体和关系是在同一个语义空间中，作者提出一种新的策略，将实体和关系分别映射到不同的语义空间中，分别为entity space（实体空间）和relation space（关系空间）。
（虽然不同的语义空间不知道对不对，至少听起来有效果，训练的结果也可以）
TransR 是清华大学刘知远、孙茂松老师团队提出来的，发表在 2015 年的 AAAI 上。创新点是将 TransH 的投影到超平面更进一步——投影到空间，本质是将投影向量换为投影矩阵，实体还是用一个向量表示，关系用一个向量和一个矩阵表示。效果提升并不大，但计算量显著增大。
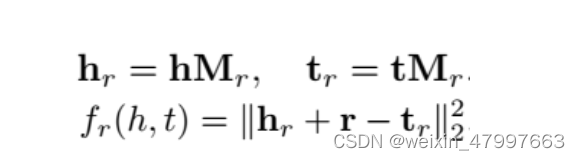
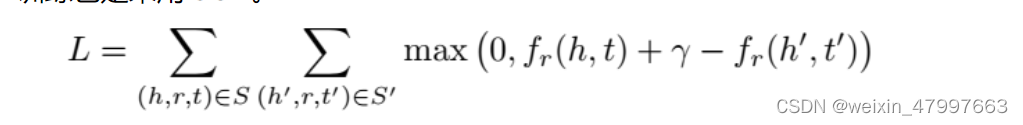
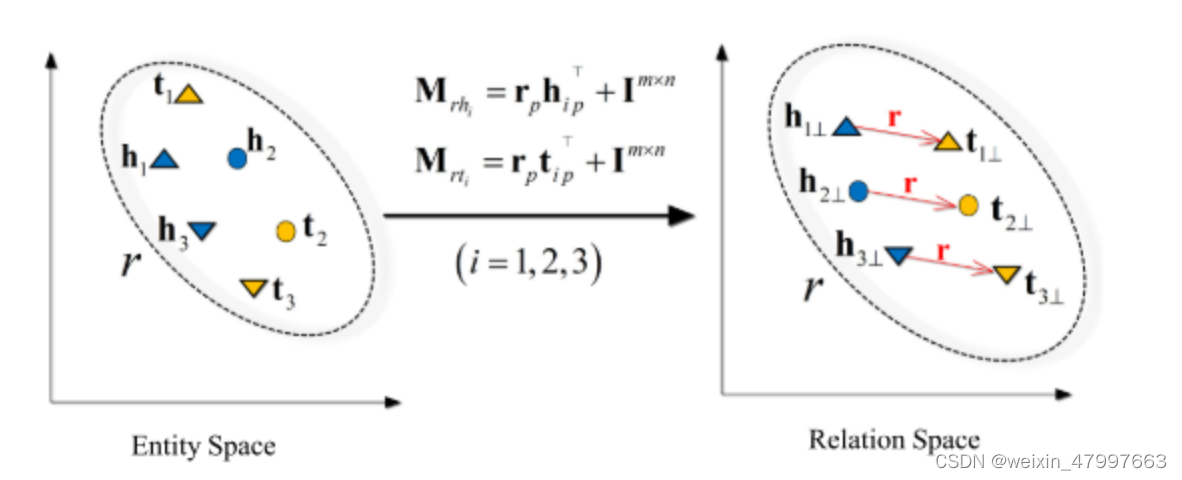
在这里插入图片描述

transD

https://blog.csdn.net/u013602059/article/details/107486941
实际上之前的模型，打分函数的转换都只是关注于关系，很少考虑到实体本身对模型的贡献，同时我们应该发现实体对结果的影响，本质上这些模型的改进方式都是通过修改不同的映射方式，来找到h-r-t间的关系，所以很常见的通过增加参数的方法来达到这一目的，考虑实体对映射过程的印象

在这里插入图片描述