0. 简介

在激光雷达的特征提取中，对整帧的点云数据进行分割是至关重要的，但是非常明显的是在3D场景中，捕获的点云通常是稀疏且非结构化的，分割有可能误分割或者漏分割。今天我们来看一下22年的论文《FEC: Fast Euclidean Clustering for Point Cloud Segmentation》，这篇文章中提出一种新颖的快速欧几里得聚类算法，同时据作者说易于实现，具体只有40行的CPP代码。目前作者代码还没有开源，说是accept后就开源。虽然这篇文章并没有被大量的关注，但是从小代码，即插即用等特点，这给我们可以通过文章学习它的详细思想以及算法的可能性。

1. 文章贡献

从整篇文章来看，该算法在现有工作中使用的聚类方案之上应用了逐点方案。文中在一开始就提到相比于传统的聚类方法，速度提升了100多倍

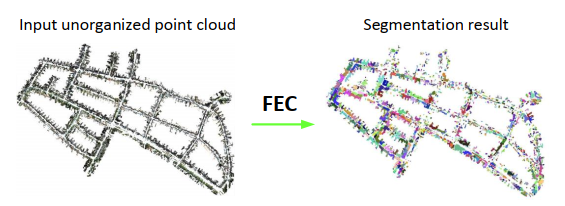
由于深度学习对点云的学习分割仍然还是比较耗资源的，所以使用传统的形态学分割仍然存在广泛的应用，通过对点云完成聚类，以区分不同的语义标签以及具有相同语义标签的各种实例。文中提到目前点云分割分为三大类：

基于区域增长的方法，主要思想是分割具有均匀几何特性的点云，首先选择种子点，然后合并相邻点，如果它们在表面点属性（如方向、表面法线和曲率）方面具有相似性，但是这些方法对初始种子的位置和边界附近法线和曲率的不准确估计非常敏感，这会导致过度分割或欠分割。
基于聚类的方法。聚类算法根据元素的相似性将元素划分为类别，可应用于点云分割。因此，K均值、均值漂移、DBSCAN和欧几里德聚类提取（EC）常被用于这项任务，尽管基于聚类的方法简单，但点云中每个点的高迭代率导致了高计算负担并降低了效率。
基于深度学习的方法。目前除了传统的点云方法以外，还有使用深度学习或投影到二维图像中，以分割点云中的实例，基于深度学习的方法通常存在运行时间长和处理大规模点云的问题。

而文中的方法是属于聚类方法的一种变种，针对现有工作中应用的聚类方案使用逐点聚类。与之前的算法对比，实现了类似的质量，但比现有工作加快了100倍。

2. 算法推导

2.1地面滤除

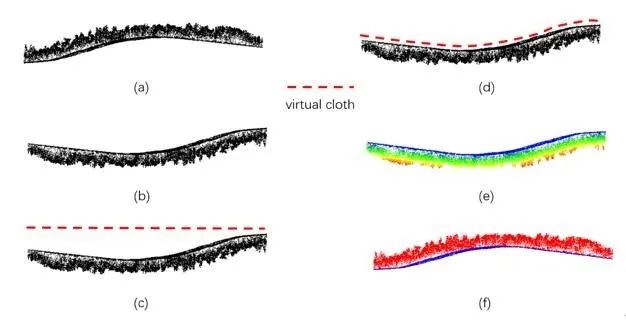
首先文中提到会先对地面点进行滤除，虽然说是地面滤除，但是如果说我们需要实际上提取车道线点时候，可以直接使用地面提取，然后再对地面的特征点进行提取。文中提到使用了cloth simulation filter来提取和滤除接地点云。

CSF csf;
//step 1 Input the point cloud
csf.readPointsFromFile(terr_pointClouds_filepath);

clock_t start, end;
start = clock();

//In real application, the point cloud may be provided by main program
//csf.setPointCloud(pc);//pc is PointCloud class

//step 2 parameter setting
csf.params.bSloopSmooth = ss;
csf.params.class_threshold = atof(class_threshold.c_str());
csf.params.cloth_resolution = atof(cloth_resolution.c_str());
csf.params.interations = atoi(iterations.c_str());
csf.params.rigidness = atoi(rigidness.c_str());
csf.params.time_step = atof(time_step.c_str());

//step3 do filtering
std::vector<int> groundIndexes, offGroundIndexes;
if (argc == 2 && strcmp(argv[1], "-c")==0)
{
    std::cout << "Export cloth enabled." << std::endl;
    csf.do_filtering(groundIndexes, offGroundIndexes, true);
}
else
{
    csf.do_filtering(groundIndexes, offGroundIndexes, false);
}


end = clock();
double dur = (double)(end - start);
printf("Use Time:%f\n", (dur / CLOCKS_PER_SEC));

csf.savePoints(groundIndexes,"ground.txt");
csf.savePoints(offGroundIndexes, "non-ground.txt");

2.2 快速欧几里得聚类

与EC类似，我们使用欧几里得（L2）距离度量来测量无组织点云的接近度，并将相似性分组到同一聚类中，可以描述为

$min\|\mathbf{P}_i - \mathbf{P}_{i'}\|_2 \geqslant d_{th}$

伪代码步骤为：

流程整体来说还是比较清楚的，首先会将 $\mathbf{P}_i$ 的label全部置零，然后分割的 $se gL ab$ 初始化为1，然后遍历所有的点，当发现遍历的点中label为0，则去找最近的关联点 $\mathbf{P}_{NN}$ 。如果存在有点不为0，则找到最小的label值，这就代表存在联通。如果不存在则赋值，然后对 $\mathbf{P}_{NN}$ 遍历，如果找到其他的label大于 $min S e gL ab$ 的值，则再次遍历所有的带你，然后将所有其他的label值，重置为 $min S e gL ab$ 的值。