
🤵?♂? 个人主页: @计算机魔术师
👨?💻 作者简介:CSDN内容合伙人,全栈领域优质创作者。
该文章收录专栏
?— 机器学习 —?
【机器学习】logistics分类
一、线性回归能用于分类吗?
l o g i s t i c logistic logistic(数理逻辑)回归算法(预测离散值 y y y 的 非常常用的学习算法
假设有如下的八个点( y = 1 或 0 ) y=1 或 0) y=1或0),我们需要建立一个模型得到准确的判断,那么应该如何实现呢
- 我们尝试使用之前文章所学的线性回归 h θ ( x ) = θ T ? x h_\theta(x) = \theta^T*x hθ?(x)=θT?x 来拟合数据( θ \theta θ是参数列向量,注意这里的 x x x是关于 x i x_i xi?的向量,其中 x 0 = 1 , 即 x 0 ? θ 0 = 常数项 x_0=1, 即 x_0*\theta_0 = 常数项 x0?=1,即x0??θ0?=常数项),并在0~1设置一个阈值 y = 0.5 所对应的 x 0.5 值 y = 0.5 所对应的 x_{0.5} 值 y=0.5所对应的x0.5?值, x x x 大于 x 0.5 x_{0.5} x0.5? 的点则为1,否则为0,预测会得到如下粉丝直线,
上一篇文章: 【机器学习】浅谈正规方程法&梯度下降
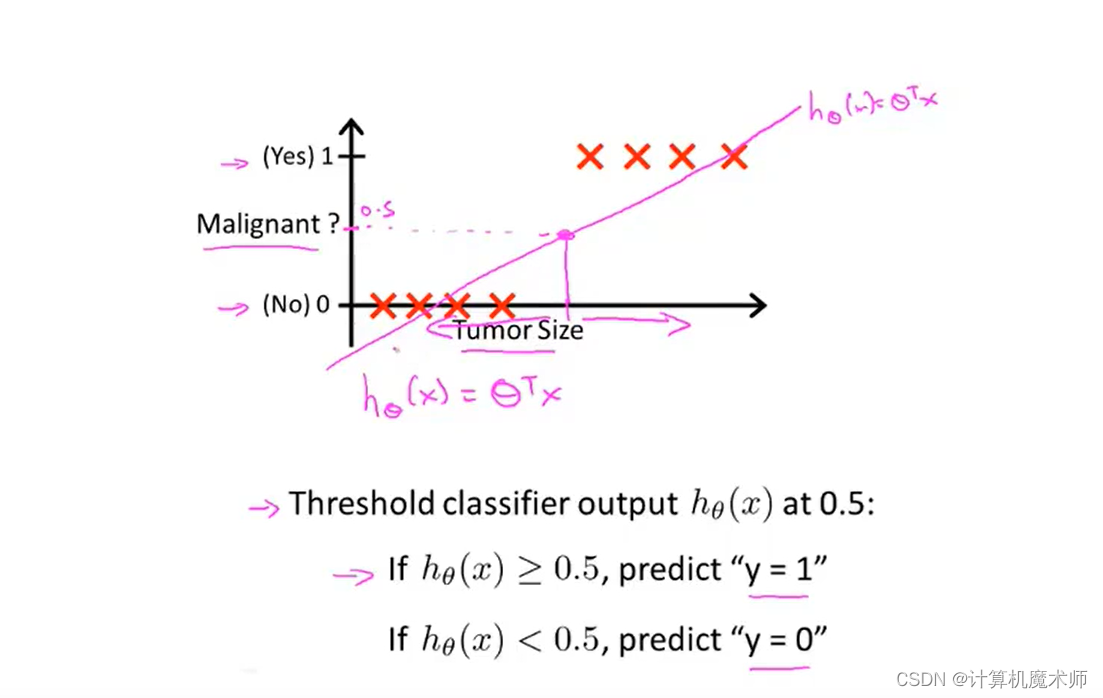
假设我们再增加一个数据点,如下图右方,按照如上算法对应的拟合直线
h
θ
(
x
)
h_\theta(x)
hθ?(x)则如下蓝色直线,此时得到错误的预测 (对于结果为1也小于
x
0.5
x_{0.5}
x0.5?)
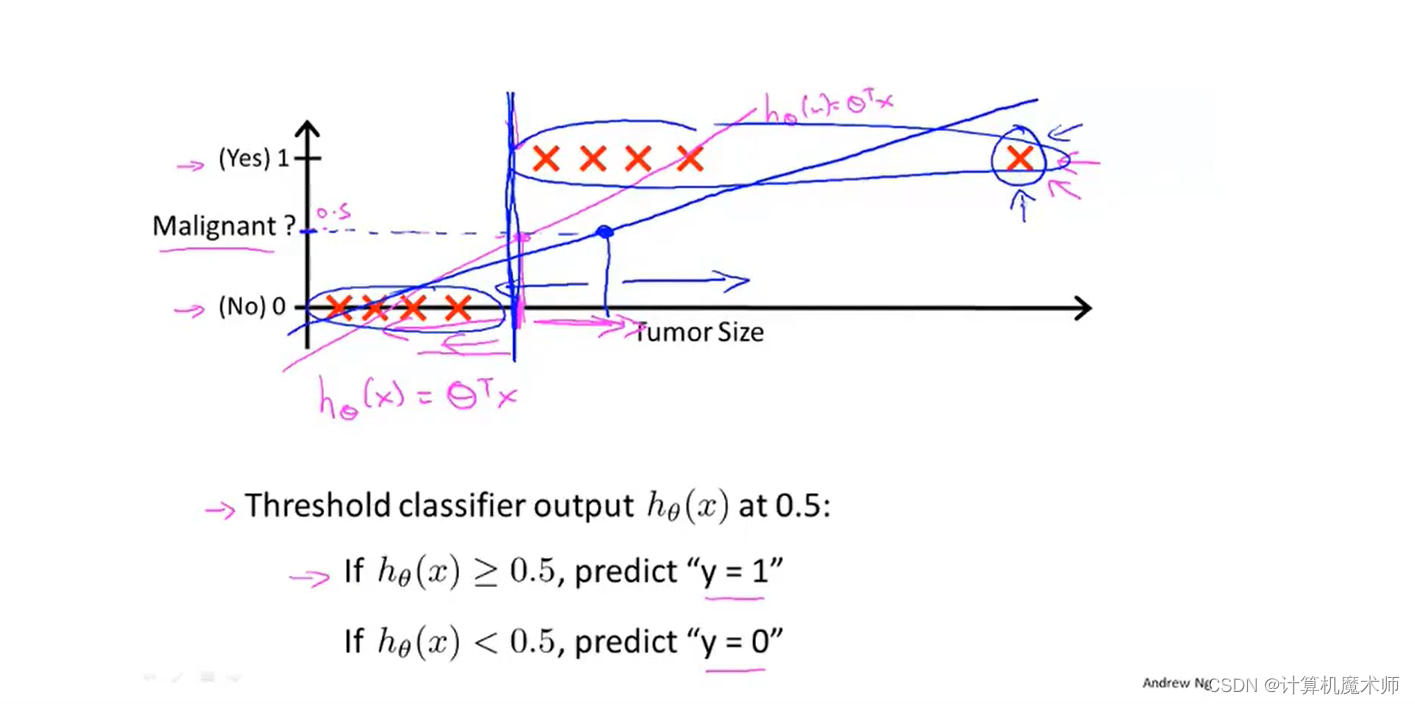
所以综上所诉,用线性回归来用于分类问题通常不是一个好主意,并且线性回归的值会远远偏离0或1,这显示不太合理。
所以梯度下降算法中引出 logistic regression 算法
二、二元分类
2.1假设函数
我们希望能把 h θ ( x ) = θ T ? x h_\theta(x) = \theta^T*x hθ?(x)=θT?x 结果在 0 ~ 1 之间,
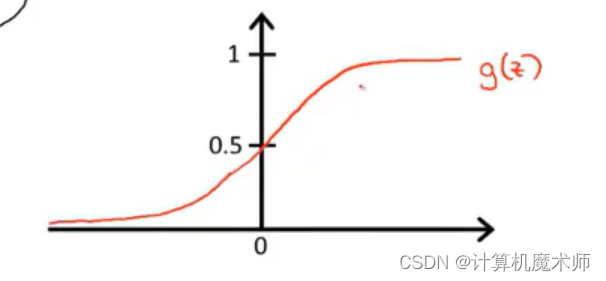
这里引入 s i g m o i d sigmoid sigmoid 函数 (也叫做 l o g i s t i c logistic logistic 函数) —— g ( x ) = 1 1 + e ? x g(x) = \frac{1}{1 + e ^{-x}} g(x)=1+e?x1?
s i g m o i d sigmoid sigmoid函数图像是一个区间在 0 ~ 1的S型函数, x ? ∞ x \Rightarrow\infty x?∞则 y ? 1 y\Rightarrow1 y?1, x ? ? ∞ x \Rightarrow-\infty x??∞则 y ? 0 y\Rightarrow0 y?0
- 令
h
θ
(
x
)
=
g
(
θ
T
?
x
)
=
1
1
+
e
?
θ
T
?
x
h_\theta(x) =g( \theta^T*x) = \frac{1}{1 + e ^{- \theta^T*x}}
hθ?(x)=g(θT?x)=1+e?θT?x1?
那么我们的函数结果结果就会在0 ~ 1 之间
那现在我们所要做的便是需要求得参数 θ \theta θ 拟合模型
如下图,假设肿瘤案例,如下 x x x为一个病人 同样的用列向量表示 x x x的参数,那么参数一tumorSize便是肿瘤的大小,那么我们可以假设输出结果为 0.7 ,意思就是医生会告诉这个病人很不幸,会有很大(70%)的概率得到肿瘤。
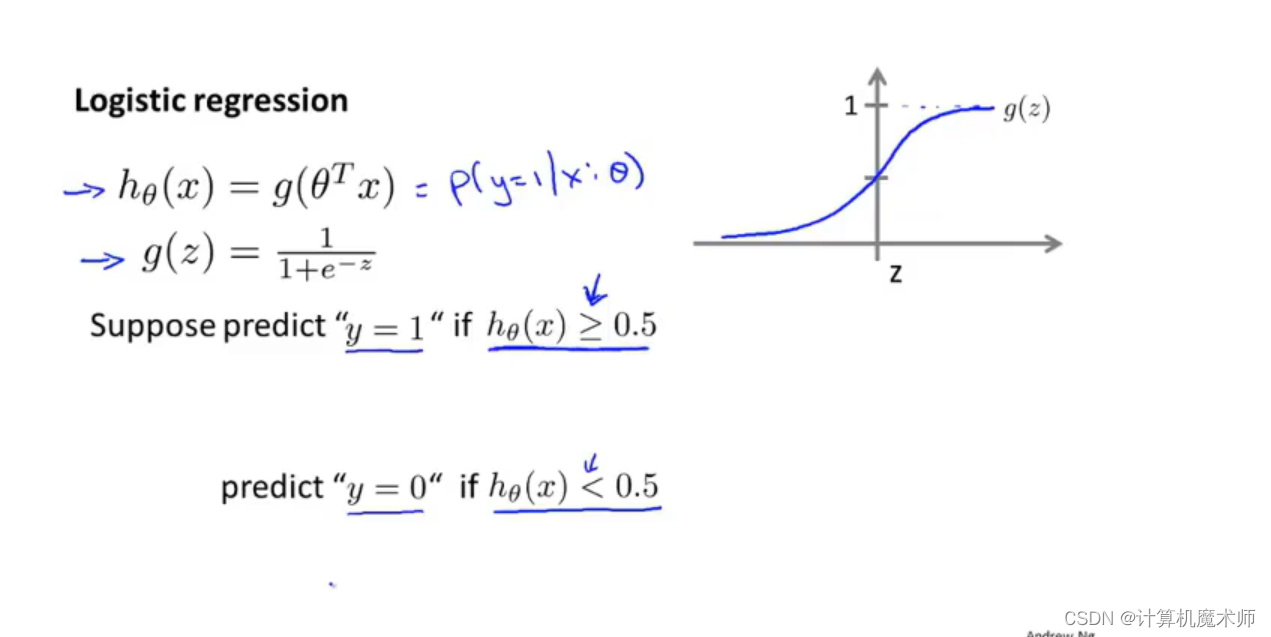
- 那么公式可以表示为 h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta(x) = P(y=1|x;\theta) hθ?(x)=P(y=1∣x;θ)
- 即在 x x x的条件下 求给定 y y y (概率参数为 θ \theta θ)的概率

那么在
y
y
y只有 0 和 1 的情况下,有如下公式 (二者为对立事件,符合全概率公式)
- P ( y = 1 ∣ x ; θ ) + P ( y = 0 ∣ x ; θ ) = 1 P(y=1|x;\theta)+ P(y=0 |x;\theta)= 1 P(y=1∣x;θ)+P(y=0∣x;θ)=1
- 1 ? P ( y = 0 ∣ x ; θ ) = P ( y = 1 ∣ x ; θ ) 1 - P(y=0 |x;\theta)= P(y=1|x;\theta) 1?P(y=0∣x;θ)=P(y=1∣x;θ)
概率结果只在0 ~ 1中
- 假设如下
那么此时我们可以设置阈值 g ( z ) g(z) g(z) = 0.5,大于 0.5 的点则为1,否则为0
即在 z < 0 z<0 z<0(即 θ T ? x \theta^T*x θT?x)中 g ( z ) g(z) g(z)< 0.5, 此时预测为0,在 z > 0 z>0 z>0(即 θ T ? x \theta^T*x θT?x) 时, g ( z ) > 0 g(z)>0 g(z)>0 预测值为1
2.1.1 案例一
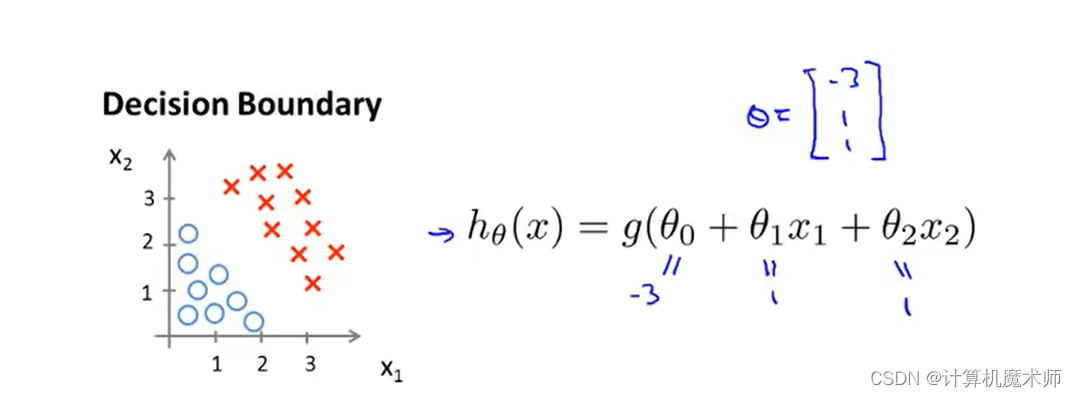
我们假设他的各个
θ
\theta
θ 参数向量参数为-3,1,1
此时如果满足
g
(
z
)
g(z)
g(z)> 0.5 , 也就是横坐标
z
z
z(这里的
z
z
z 是对应线性方程) 大于零,预测 y 为 1 条件则如下:
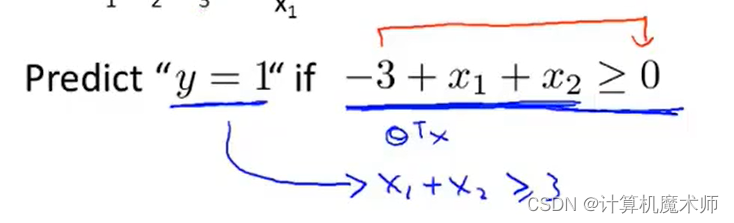
化简为条件
x
1
+
x
2
>
=
3
x_1 + x_2 >=3
x1?+x2?>=3 , 这个条件所对应的几何意义:
即一条切割线的右侧,此时
s
i
g
o
m
i
d
函数的
z
坐标
>
0
sigomid函数的z坐标>0
sigomid函数的z坐标>0 , y值 大于0.5
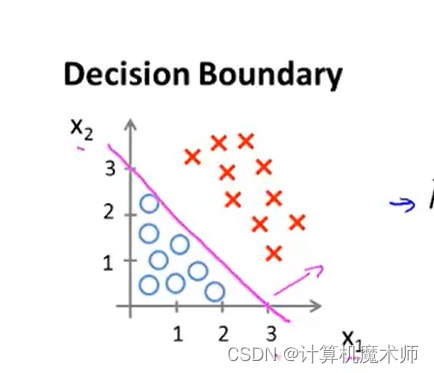
此时该切割线分割除了两个区域,分别是
y
=
0
与
y
=
1
y=0 与 y=1
y=0与y=1的 情况,我们把这条边界,称为决策边界,这些都是关于假设函数的属性,决定于其参数,与数据集属性无关

2.1.2例子二
有数据集如下:
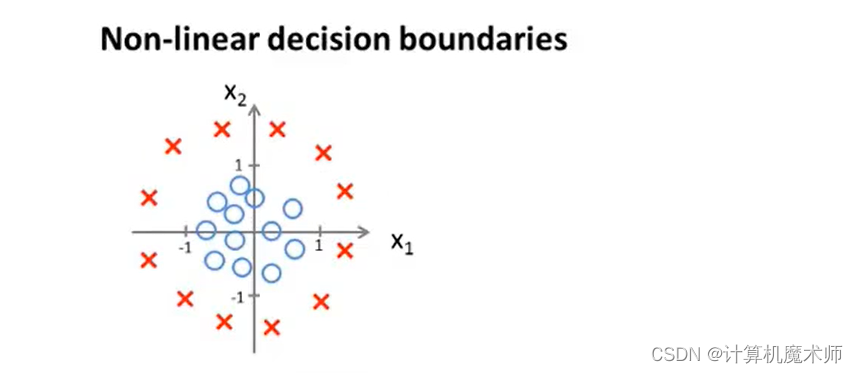
我们假设函数为多项式高阶函数,并对其参数假设赋值如下。
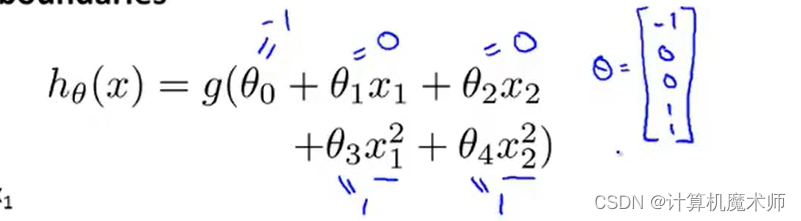
那我们的预测y=1时,
s
i
g
o
m
i
d
sigomid
sigomid横坐标
z
z
z满足条件为
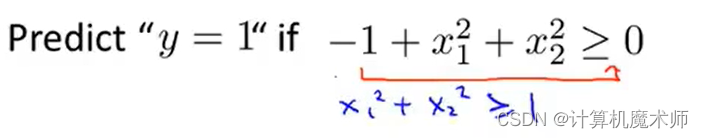
可以得到其决策边界decision boundory ——
x
1
2
+
x
2
2
=
1
x_1^2+x_2^2 =1
x12?+x22?=1
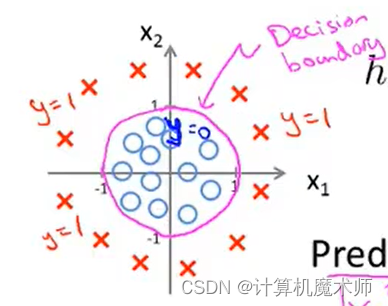
- 强调: 决策边界并不是数据集的属性,而是假设函数以及其参数的属性,数据集则是用于拟合参数
θ
\theta
θ
不同的高阶多项式 会得到不一样的决策边界
如:
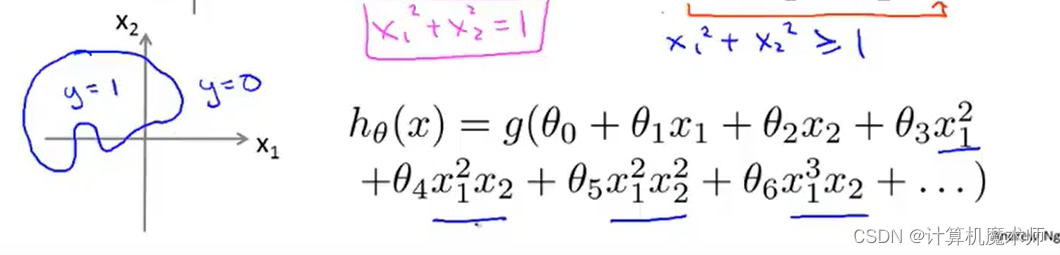
2.2 拟合logistic回归参数 θ i \theta_i θi?
- 代价函数
我们给定如数据集
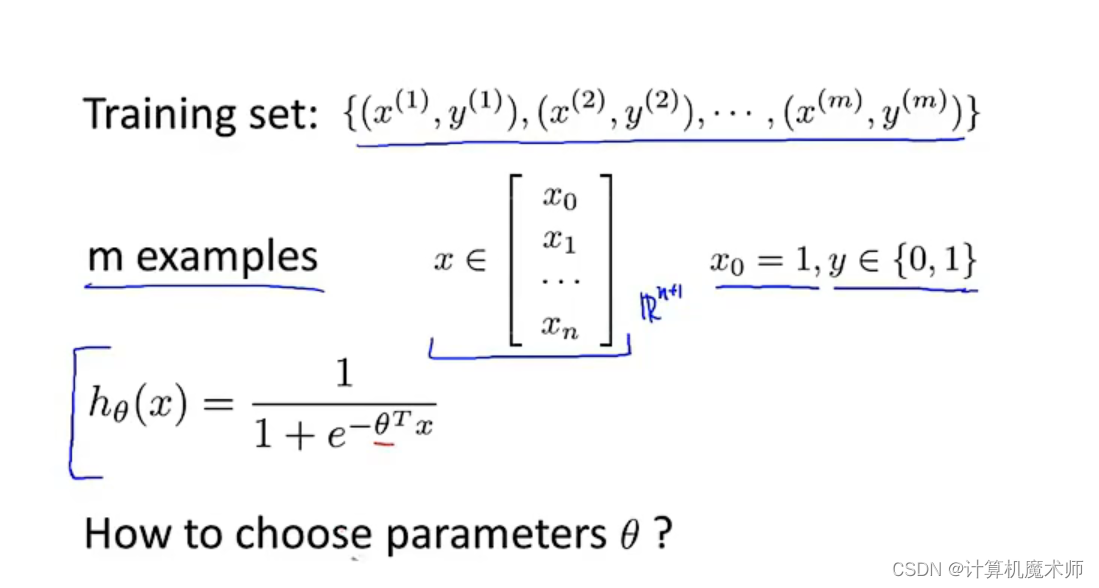
有
m
m
m个样本,同样将每一个
x
x
x用
n
+
1
n+1
n+1维向量表示(向量每个元素即特征,其中
x
0
为
1
x0为1
x0为1 ) 分类标签
y
y
y只有 0,1结果
- 那么我们如何选择参数 θ \theta θ呢?
在往篇文章中我们线性回归的均方差代价函数可以变化如下:

简化函数,我们省略上标
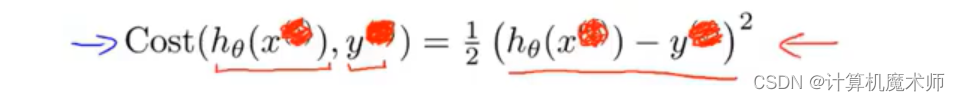
因为
s
i
g
o
m
i
d
sigomid
sigomid 是复杂的非线性函数,如果直接以函数作为代价函数,那么所求模型对应代价函数为非凹函数,会有非常多的局部最优,如下图
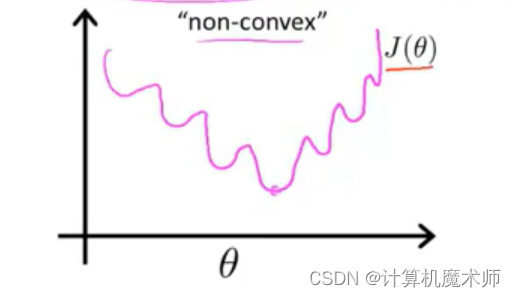
我们不能保证其可以下降到函数最优
我们往往希望找到如下的凹型代价函数,以可以找到参数最优。
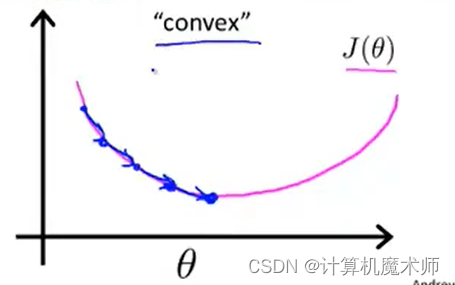
故我们需要找到另外的代价函数保证我们可以找到全局最小值
三、logistic代价函数

3.1 当 y = 1 y=1 y=1代价函数图像
对该代价函数,我们可以画出当
y
=
1
y=1
y=1时的图像。(由于
s
i
g
o
m
i
d
sigomid
sigomid 函数值域在0~1,对应代价函数横坐标为0 ~1)
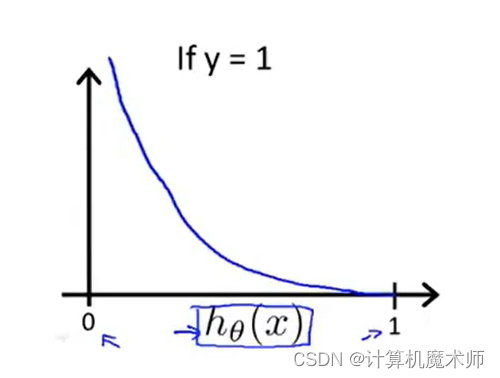
为了方便理解我们可以画出,对数函数的图像
l
o
g
(
z
)
log(z)
log(z) (
z
=
h
θ
(
x
)
)
z = h_\theta(x))
z=hθ?(x)) )
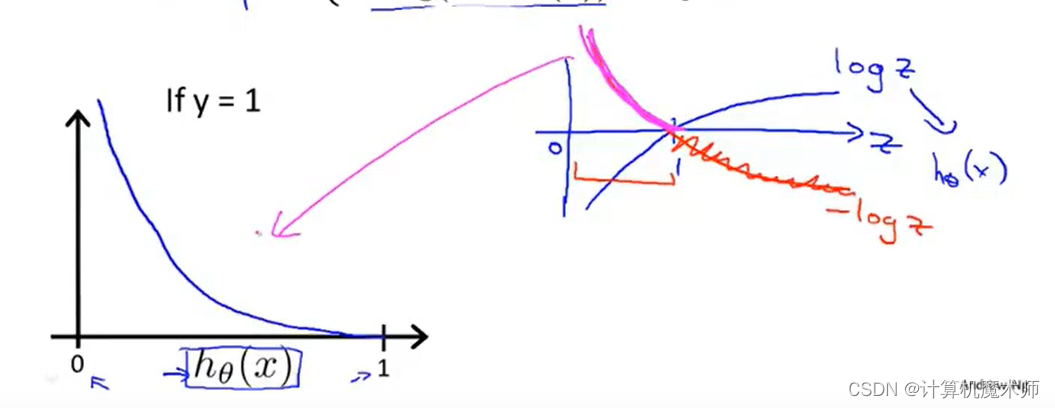
- 从图中我们也可以看到作为代价函数 很好的性质
-
当 C o s t ? 0 Cost \Rightarrow 0 Cost?0时,即代价函数为0,此时有 h θ ( x ) ? 1 h_\theta(x)\Rightarrow1 hθ?(x)?1 即模型拟合优秀
-
当 C o s t ? ∞ Cost \Rightarrow\infty Cost?∞时,即代价函数 ? ∞ \Rightarrow\infty ?∞,此时 h θ ( x ) ? 0 h_\theta(x) \Rightarrow 0 hθ?(x)?0即为 。此时说明模型拟合非常差
显然当 y = 1 y=1 y=1 时 这个代价函数满足我们的要求

3.2 当 y = 0 y=0 y=0代价函数图像
对应
y
=
0
y=0
y=0的情况下:
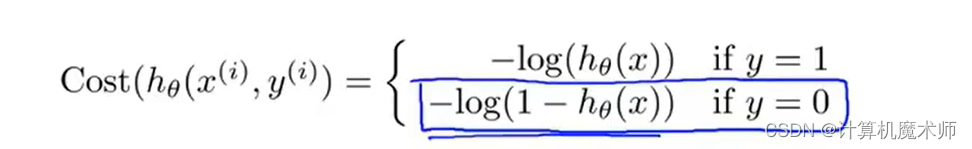
- 如下图
-
当 C o s t ? 0 Cost \Rightarrow 0 Cost?0时,即代价函数为 ? 0 \Rightarrow0 ?0,此时有 h θ ( x ) ? 0 h_\theta(x)\Rightarrow0 hθ?(x)?0 即模型拟合优秀
-
当 C o s t ? ∞ Cost \Rightarrow\infty Cost?∞时,即代价函数 ? ∞ \Rightarrow\infty ?∞,此时 h θ ( x ) ? 1 h_\theta(x) \Rightarrow 1 hθ?(x)?1即为 。函数惩罚很大
同样的符合代价函数性质
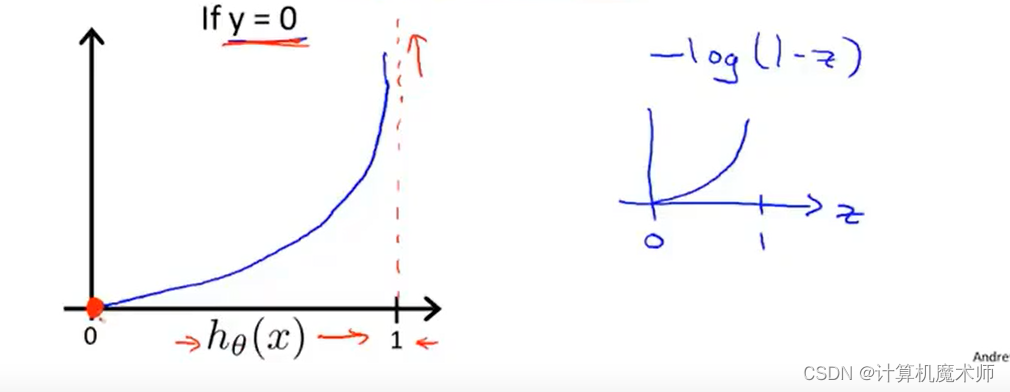
至此,我们定义了关于单变量数据样本的分类代价函数,我们所选择的代价函数可以为我们解决代价函数为非凹函数的问题以及求解参数最优,接下来我们使用梯度下降算法来拟合 l o g i s t i c logistic logistic 算法
四、 代价函数与梯度下降
为了避免让代价函数分为 y = 1 , y = 0 y = 1,y= 0 y=1,y=0两种情况 ,我们要找一个方法来把这两个式子合并成一个等式,以便更简单写出代价函数,并推导出梯度下降。
公式如下图蓝色字体公式:

由于 y 只有两个情况 0,1 ,利用该性质 当y = 1 时,y=0情况的多项式消去,y = 0 时同理,这样就成功表达了两种不同情况的函数
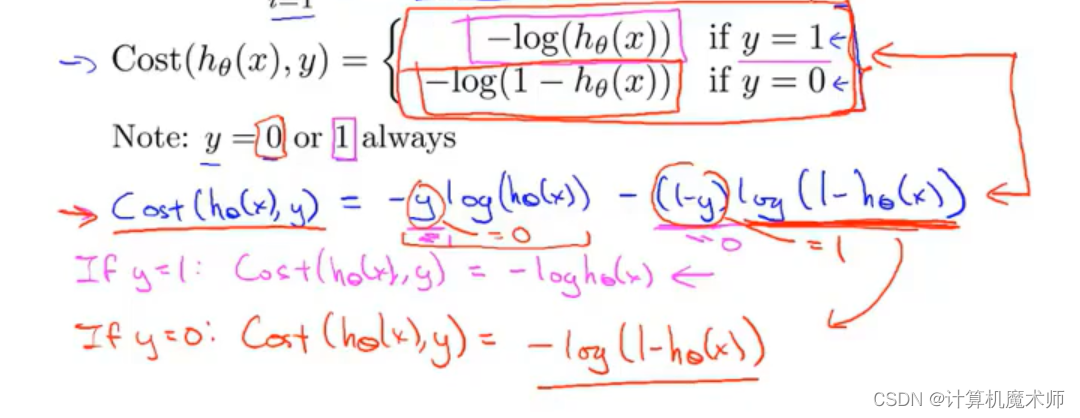
- 通过将式子合并为一个等式,代价函数(cost function) 变化为如下(参考:统计学的极大似然法:
为不同模型已知数据寻找参数的方法,即选取概率最大的参数)
最大似然函数参考文章

同样,我们为了求最小化代价函数以拟合参数
θ
\theta
θ,使用梯度下降

- 同样,将微积分求其偏导

- 并用此公式更新每个参数 (注意是:同步更新)

4.1 线性回归与logistic回归的梯度下降规则
我们可以惊奇的发现以上公式与线性回归时所用来梯度下降的方程一样
那么线性回归和logistic回归是同一种算法吗?
线性回归和logistic在梯度下降更新的函数区别在于: h θ ( x i ) h_\theta(x^i) hθ?(xi)
- 对于线性回归 : h θ ( x ) = θ T ? x h_\theta(x) = \theta^T*x hθ?(x)=θT?x
- 对于logistic回归: h θ ( x ) = 1 1 + e ? θ T ? x h_\theta(x) = \frac{1}{1 + e ^{- \theta^T*x}} hθ?(x)=1+e?θT?x1?
虽然在梯度下降算法看起来规则相同,但假设的定义发生了变化,所以梯度下降和logistic回归是完全不一样的算法
- 我们用此算法更新各个参数,可以通过for进行实现,也可以通过向量化进行实现。
关于向量化,可以参考文章 【机器学习】向量化计算 – 机器学习路上必经路

同样的,在对于线性回归的梯度下降中,我们使用到了特征缩放数据标准化,同样的,这对于
l
o
g
i
s
t
i
c
logistic
logistic 回归算法同样适用。
数据标准化可参考文章: 【机器学习】梯度下降之数据标准化
五、高级优化算法
高级优化算法,与梯度下降相比能够大大提高
l
o
g
i
s
t
i
c
logistic
logistic 回归速度,也使得算法更加适合大型数据集机器学习问题。
除了使用梯度下降算法,还有诸多如下算法

优点如下
- 不需要选择学习率 α \alpha α ( 存在智能内循环,智能选择最佳的学习率 α \alpha α
- 下降速率快得多
缺点
- 太过于复杂了
在实际解决问题中,我们很少通过自己编写代码求平方根或者求逆矩阵,我们往往都是使用别人写的好的数据科学库,如numpy
有如下例子(求两个参数)

我们可以通过梯度下降来求得参数,如下求偏导:

octave代码实现如下;
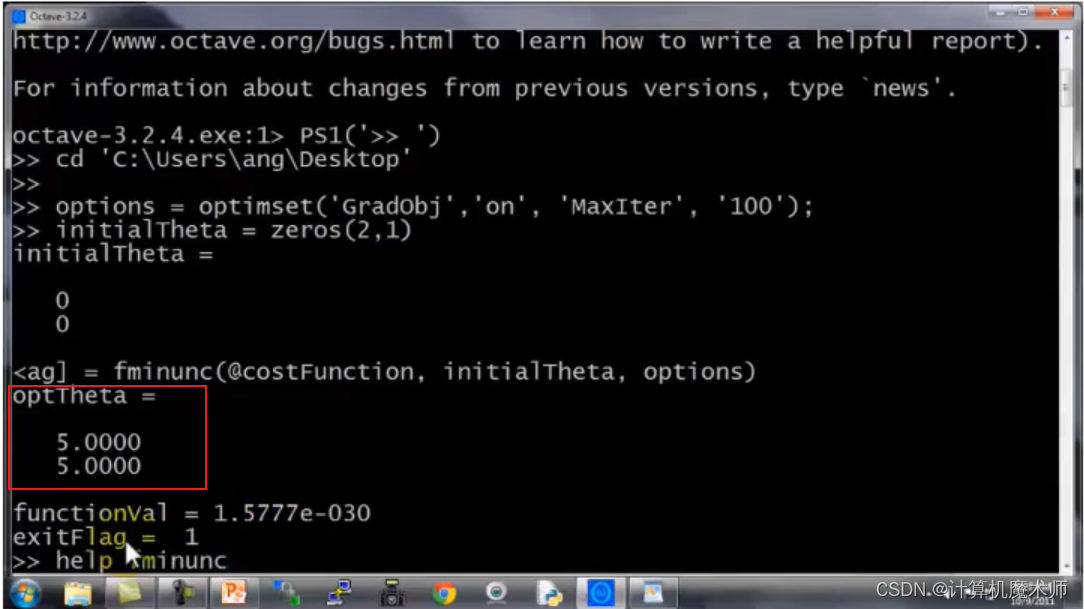
这是一个简单的二次代价函数,现在我们如何将其用在logistic回归算法中呢?
在logistic回归中,我们使用如下的
θ
\theta
θ参数向量 (使用参数向量化)

所以在实现这些高级算法,其实是使用不同的高级库函数,虽然这些算法在调试过程中,更加麻烦,但是其速度远远大于梯度下降,所以面对机器学习问题中,往往使用这些算法。
六、多元分类:一对多
例如将邮件分为亲人,朋友,同事。例如将天气分类,下雨,晴天等、我们可以将这些用数字0,1,2表达,以上这些都是多类别分类
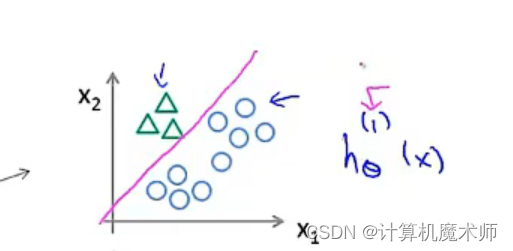
与二分类图像不同(右图)
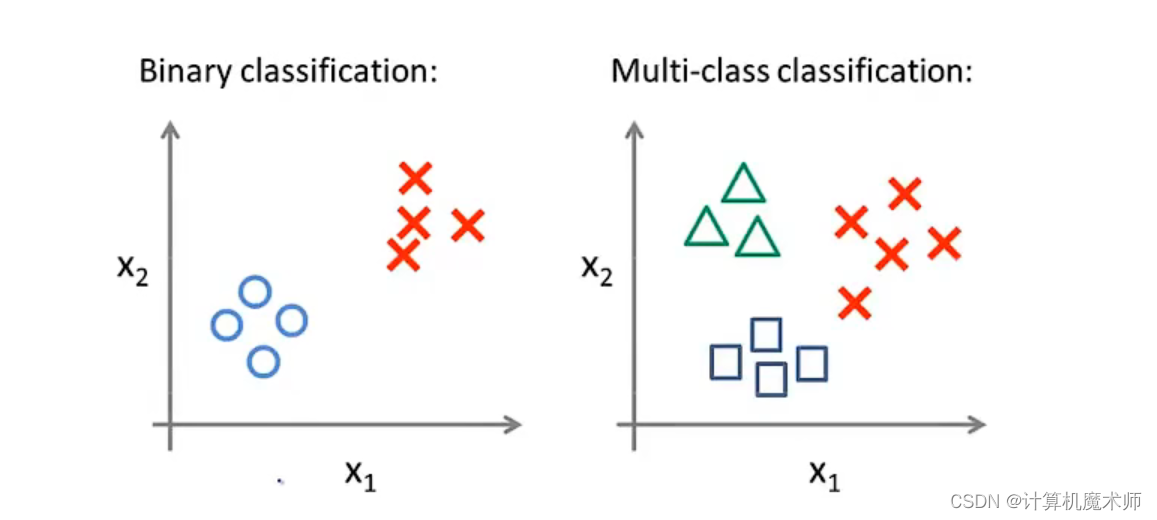
首先,我们将该数据集划分为三类
我们要做的就是将这数据集转换为三个独立的二元分类问题, 我们将创建一个新的**”伪“训练集**,其中第二类第三类为负类,第一类为正类(如下图右侧)
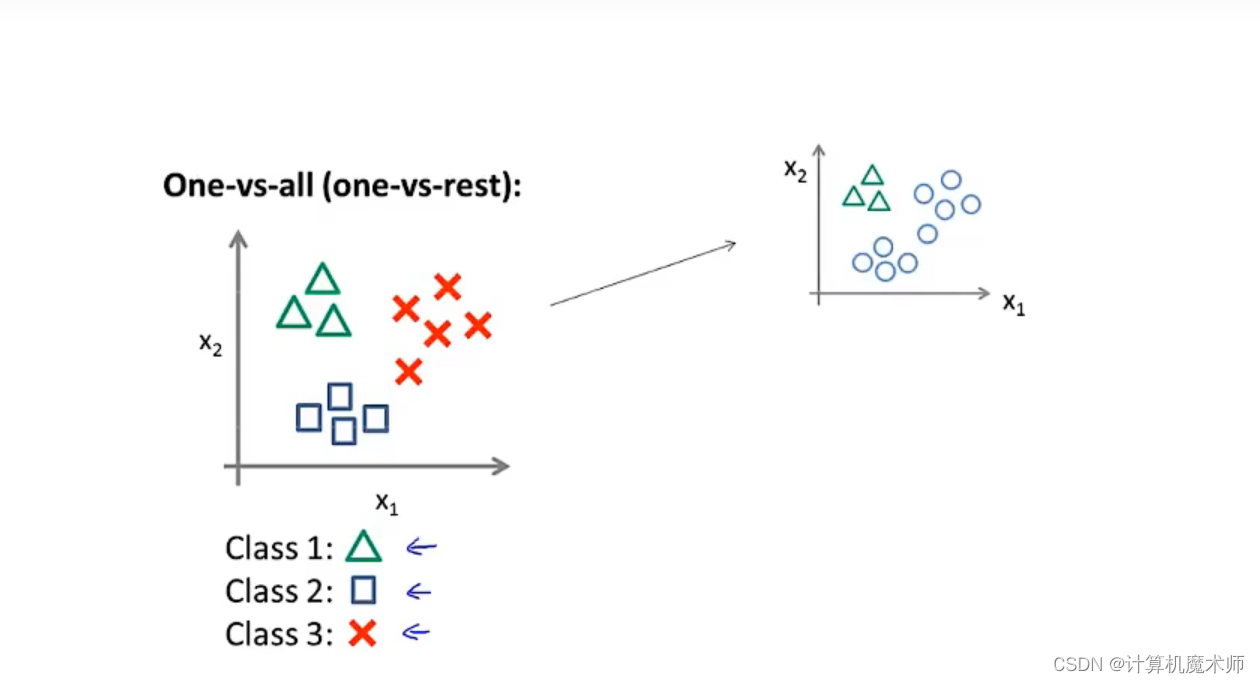
并拟合一个分类器
h
θ
1
(
x
)
h_\theta^1(x)
hθ1?(x),接下来我们来实现一个标准的逻辑回归分类器,通过训练,我们可以得到一个决策边界
- 同理,将其他两类样本如上创建
伪数据集,以及对应的拟合分类器,进行一个标准的逻辑回归分类器,得到对应边界

总而言之,我们拟合出了三个分类器
h θ i ( x ) = P ( y = i ∣ x ; θ ) ( i = 1 , 2 , 3 ) h_\theta^i(x) = P(y=i|x;\theta) (i=1,2,3) hθi?(x)=P(y=i∣x;θ)(i=1,2,3)
每个分类器都对应与之的情况训练,y = 1, 2, 3 的情况
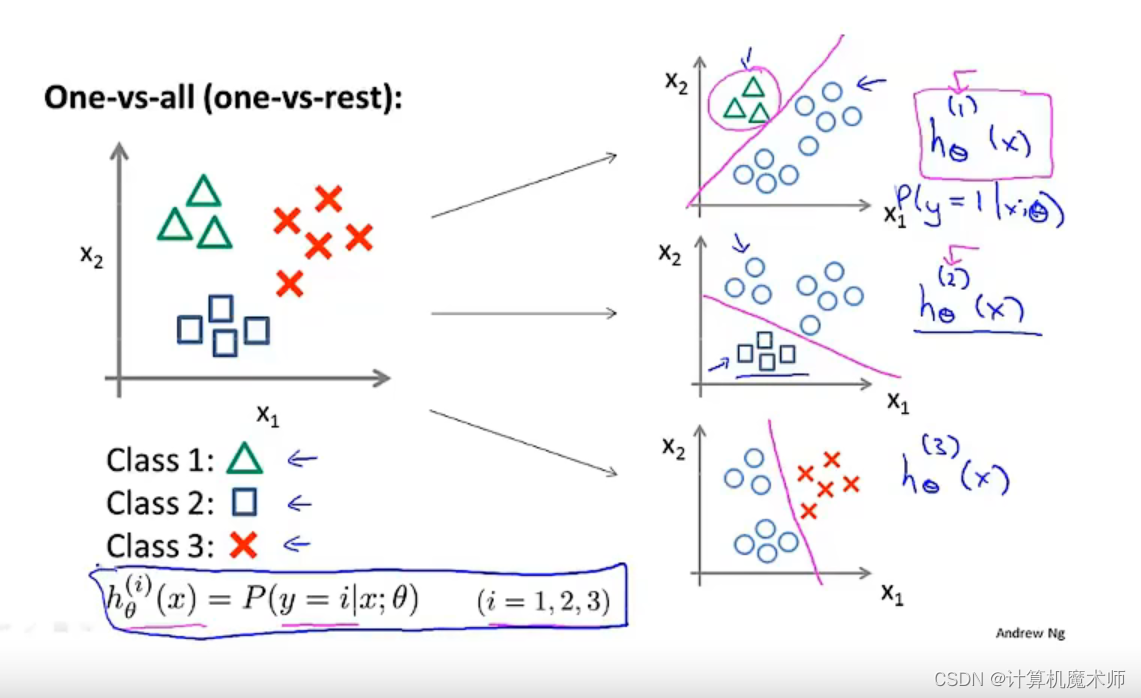
我们训练了逻辑回归分类器 h θ i ( x ) = P ( y = i ∣ x ; θ ) ( i = 1 , 2 , 3 ) h_\theta^i(x) = P(y=i|x;\theta) (i=1,2,3) hθi?(x)=P(y=i∣x;θ)(i=1,2,3),用于预测 y = i y= i y=i 的概率,为了做出预测,我们向分类器输入一个 x x x,期望获得预测,我们需要在这三个回归分类器中运行输入 x x x,选出结果中概率最大的一个(最可信)的那个分类器,就是我们要的类别。