[人工智能]神经网络(深度学习)----MLPClassifier库的初尝试

神经网络(深度学习)

一些被称为神经网络的算法以"深度学习"为名成为主流。

虽然深度学习在许多机器学习应用中都有巨大的潜力，但深度学习算法往往经过精确调整，只适用于特定的使用场景。

这里只讨论一些相对简单的方法，即用于分类和回归的多层感知机(multilayer perceptron, MLP)，它可以作为研究更复杂的深度学习方法的起点。MLP 也被称为前馈神经网络，有时也被称为神经网络。

神经网络模型

MLP 可以被视为广义的线性模型，执行多层处理后得到结论。

或许还记得线性回归的预测公式为:

$$\hat{y}=w[0]?x[0]+w[1]?x[1]+...+w[p]?x[p]+b$$

简单来说，$\hat{y}$是输入特征x[0]到x[p]的加权求和，权重为学到的系数w[0]到w[p]。

可以将该公式可视化，如下图

import mglearn                               #导入mglearn库
from IPython.display import display         #导入display可视化方法

display(mglearn.plots.plot_logistic_regression_graph())         #绘制逻辑回归图形

上图中，左边的每个结点代表一个输入特征，连线代表学到的系数，右边的结点代表输出，是输入的加权求和。

在 MLP 中，多次重复这个计算加权求和的过程，首先计算代表中间过程的隐单元(hidden unit)，然后再计算这些隐单元的加权求和并得到最终结果。

如下图

display(mglearn.plots.plot_single_hidden_layer_graph())         #输出隐层的图形结果

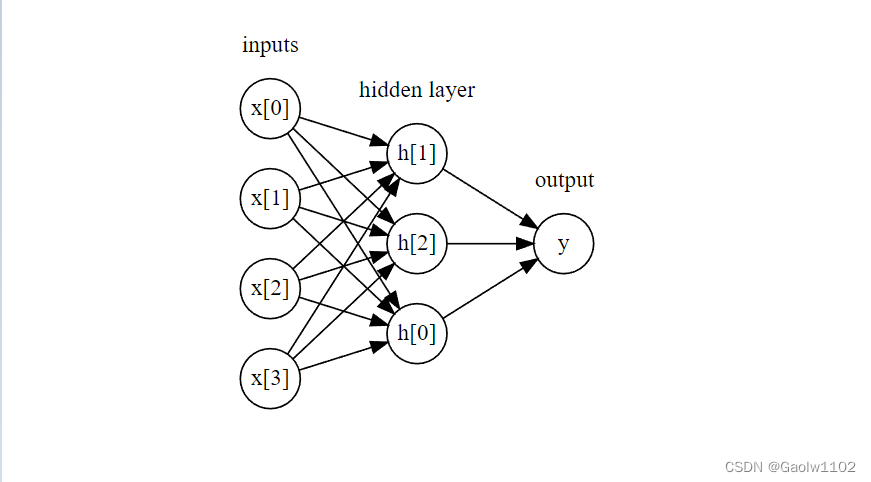
这个模型需要学习更多的系数(也叫做权重): 在每个输入与每个隐单元(隐单元组成了隐层)之间有一个系数，在每个隐单元与每个输出之间也有一个系数。

从数学的角度看，计算一系列加权求和与只计算一个加权求和是完全相同的，因此，为了让这个模型真正比线性模型更为强大，这里还需要一个技巧。

在计算完每个隐单元的加权求和之后，对结果再应用一个非线性函数----通常为校正非线性(rectifying nonlinearity, 也叫校正线性单元或relu)或正切双曲线(tangens hyperbolicus, tanh)。

之后将该函数的结果加权求和，得到输出$\hat{y}$。

该两个函数的可视化图形如下

import matplotlib.pyplot as plt

line = np.linspace(-3,3,50)                                 #从-3到3划分为 50份
plt.plot(line, np.tanh(line), label='tanh')                 #绘制tanh图像
plt.plot(line, np.maximum(0, line), label='relu')           #绘制relu图像
plt.legend(loc='best')

plt.xlabel('x')
plt.ylabel('relu(x), tanh(x)')

Text(0, 0.5, 'relu(x), tanh(x)')

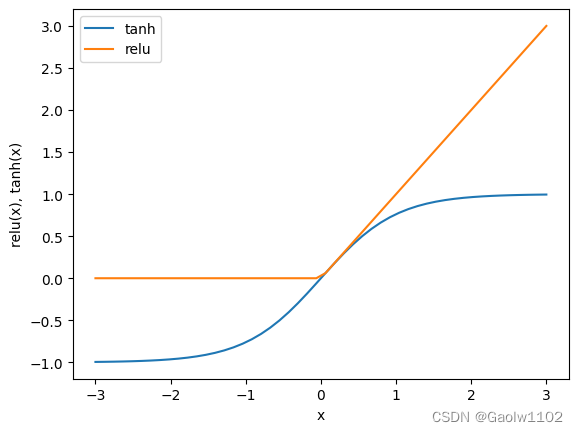
所以，对于上述的小型神经网络，计算回归问题的 $\hat{y}$ 的完整公式如下(使用tanh非线性):

$$?\begin{array}{l}h[0]=tanh(w[0,0]?x[0]+w[1,0]?x[1]+w[2,0]?x[2]+w[3,0]?x[3]+b[0])\\ h[1]=tanh(w[0,0]?x[0]+w[1,0]?x[1]+w[2,0]?x[2]+w[3,0]?x[3]+b[1])\\ h[2]=tanh(w[0,0]?x[0]+w[1,0]?x[1]+w[2,0]?x[2]+w[3,0]?x[3]+b[2])\\ \hat{y}=v[0]?h[0]+v[1]?h[1]+v[2]?h[2]+b\end{array}$$

其中，w是输入x与隐层h之间的权重，v是隐层h与输出$\hat{y}$之间的权重。

权重 w 和权重 v 需要从数据中学习得到，x 是输入特征，$\hat{y}$是计算得到的输出，h是计算的中间结果。

神经网络可以有多个隐层，如下图所示

mglearn.plots.plot_two_hidden_layer_graph()

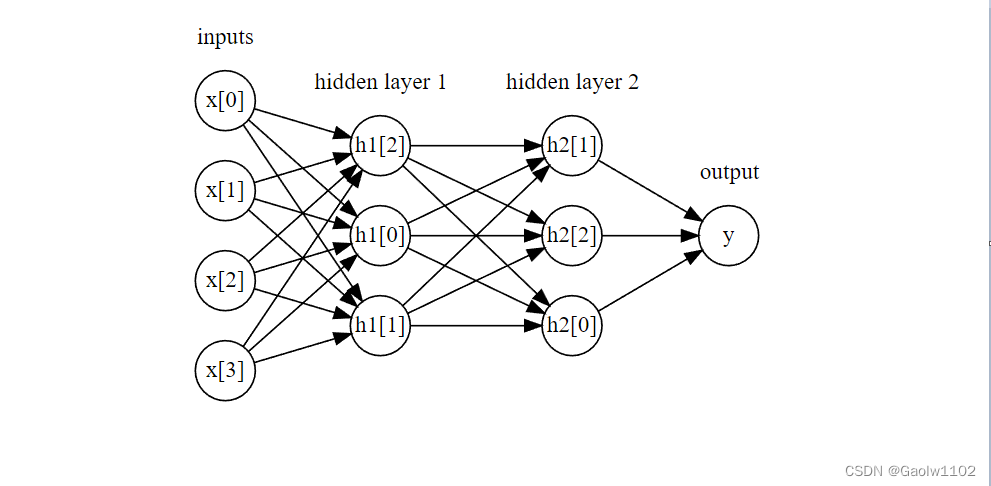
这些由许多计算层组成的大型神经网络，正是术语"深度学习"的灵感来源。

神经网络调参

假如将MPLClassifier应用到前面用过的two_moons数据集上，会出现什么效果呢?

默认情况(1层hidden层，包含100个隐单元hidden unit)

from sklearn.datasets import make_moons                          #导入数据集
from sklearn.neural_network import MLPClassifier                #导入前馈神经网络分类器
from sklearn.model_selection import train_test_split             #导入数据集分离函数
import mglearn

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)      #获取到数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train)         #训练数据集
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)                      #绘制出分界线
mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train)                     #显示出所有点

plt.xlabel('feature 0')
plt.ylabel('feature 1')

Text(0, 0.5, 'feature 1')

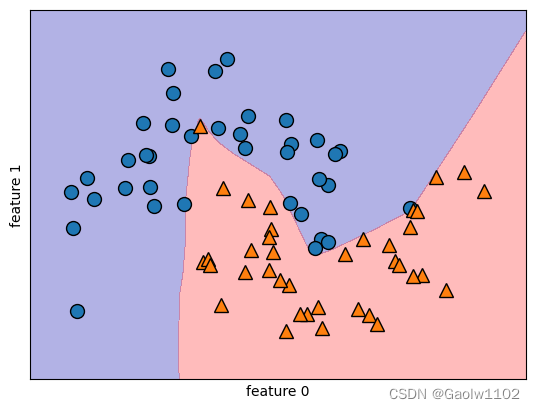
可以看到，神经网络分类的效果十分有效，学到的决策边界完全是非线性的，但相对平滑。

减少隐单元个数

默认情况下，MLP使用100个隐结点，但对于这个小型数据集来说已经相当多了。我们可以减少其数量，仍然可以得到好的结果。

from sklearn.datasets import make_moons                          #导入数据集
from sklearn.neural_network import MLPClassifier                #导入前馈神经网络分类器
from sklearn.model_selection import train_test_split             #导入数据集分离函数
import mglearn

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)      #获取到数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10]).fit(X_train, y_train)        #训练数据集
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)                                        #绘制出分界线
mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train)                                              #显示出所有点

plt.xlabel('feature 0')
plt.ylabel('feature 1')

Text(0, 0.5, 'feature 1')

只有10个隐单元时，决策边界看起来更加参差不齐。默认的非线性是relu。

如果使用单隐层，那么决策函数将有10个直线段组成。如果想要得到更加平滑的决策边界，可以添加更多的隐单元，添加第二个隐层或者使用tanh非线性。

添加多层隐层

如下代码，添加第二个隐层，每个隐层包含10个隐单元(激活函数为relu):

from sklearn.datasets import make_moons                          #导入数据集
from sklearn.neural_network import MLPClassifier                #导入前馈神经网络分类器
from sklearn.model_selection import train_test_split             #导入数据集分离函数
import mglearn

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)      #获取到数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10, 10]).fit(X_train, y_train)       #训练数据集,此时存在2个隐层
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)                                           #绘制出分界线
mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train)                                                 #显示出所有点

plt.xlabel('feature 0')
plt.ylabel('feature 1')

Text(0, 0.5, 'feature 1')

切换激活函数

依旧添加第二个隐层，每个包含10个单元，这次使用tanh非线性(激活函数为tanh):

from sklearn.datasets import make_moons                          #导入数据集
from sklearn.neural_network import MLPClassifier                #导入前馈神经网络分类器
from sklearn.model_selection import train_test_split             #导入数据集分离函数
import mglearn

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)      #获取到数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

mlp = MLPClassifier(solver='lbfgs', random_state=0, activation='tanh', hidden_layer_sizes=[10, 10])        #训练数据集,2个隐层,tanh函数
mlp.fit(X_train, y_train)                                                                                   #训练数据
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)                                         #绘制出分界线
mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train)                                               #显示出所有点

plt.xlabel('feature 0')
plt.ylabel('feature 1')

Text(0, 0.5, 'feature 1')

正则化操作

MLP分类器中也存在alpha正则化参数，默认值为0.0001。

同前，alpha越小，正则化程度越小，模型较为复杂；alpha越大，正则化程度越大，模型较为简单。

fig, axes = plt.subplots(2, 4, figsize=(20, 8))
for axx, n_hidden_nodes in zip(axes, [10, 100]):                          #循环所有显示面板
    for ax, alpha in zip(axx, [0.0001, 0.01, 0.1, 1]):                    #不断变更alpha正则化参数
        
        #实例化MLP神经网络
        mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[n_hidden_nodes, n_hidden_nodes], alpha=alpha)
        mlp.fit(X_train, y_train)                                                                                  #训练数据
        mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax)                                 #绘制分界线
        mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train, ax=ax)                                       #绘制所有的数据点
        ax.set_title('n_hidden=[{}, {}]\nalpha={:.4f}'.format(n_hidden_nodes, n_hidden_nodes, alpha))              #添加标签
        
        

现在，我们可以明白，控制神经网络复杂度的方法有很多种:

• 隐层的个数
• 每个隐层的隐单元
• 正则化alpha

随机化种子的影响

需要注意的是，在初始化定义MLP神经网络时，特征或隐单元的权重一般为随机设置的，这种初始化会影响模型学到的结果。如下

fig, axes = plt.subplots(2, 4, figsize=(20, 8))
for i, ax in enumerate(axes.ravel()):
    mlp = MLPClassifier(solver='lbfgs', random_state=i, hidden_layer_sizes=[100,100])           #定义前馈神经网络模型
    mlp.fit(X_train, y_train)                                                                    #训练数据集
    mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax)                   #绘制分界线
    mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train, ax=ax)                         #绘制所有的数据点

但是若网络很大，且复杂度选择合理的话，这应该不会对精度有太大影响，但是较小的网络需要注意这一点。

MLP分类器的实际应用

现在将MLPClassifier应用在乳腺癌数据集上。测试如下:

from sklearn.datasets import load_breast_cancer               #引入数据集
from sklearn.neural_network import MLPClassifier              #引入MLP神经网络分类器
from sklearn.model_selection import train_test_split          #引入数据集分割函数

cancer = load_breast_cancer()                                  #加载数据集
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state=0)           #拆分数据集

mlp = MLPClassifier(random_state=42)                           #加载神经网络模型
mlp.fit(X_train, y_train)                                      #训练数据集

print('Accuracy on training set:{}'.format(mlp.score(X_train, y_train)))                              #输出训练集预测准确度
print('Accuracy on test set:{}'.format(mlp.score(X_test, y_test)))                                    #输出测试集预测准确度

Accuracy on training set:0.9389671361502347
Accuracy on test set:0.916083916083916

MLP的精度较好，但是没有其它的模型好。

数据预处理(缩放)

与较早的SVC例子相同，原因可能在于数据的缩放。神经网络也要求所有输入特征的变化范围相似，最理想的情况是均值为0、方差为1。

现在需要对数据进行缩放。

mean_on_training = X_train.mean(axis=0)                            #求每一列特征的平均值
std_on_training = X_train.std(axis=0)                              #求每一列特征的标准差

#training_scale数据集中的特征列均值为0，标准差为1
X_training_scale = (X_train-mean_on_training)/std_on_training        #数据集减去每个特征的均值。再除以标准差
X_test_scale = (X_test-mean_on_training)/std_on_training             #同样地对测试集数据进行测试

mlp = MLPClassifier(random_state=42)                                 #加载神经网络模型
mlp.fit(X_training_scale, y_train)                                   #训练数据集

print('Accuracy on training set:{}'.format(mlp.score(X_training_scale, y_train)))             #输出训练集预测准确度
print('Accuracy on test set:{}'.format(mlp.score(X_test_scale, y_test)))                      #输出测试集预测准确度

Accuracy on training set:0.9929577464788732
Accuracy on test set:0.965034965034965

可以看到，预测的准确度有了显著的提升。

不过存在过拟合的现象，可以加大正则化程度提高泛化程度。

增加正则程度

此时选择增加alpha的值来增大正则化，再来测试预测的准确度。

mean_on_training = X_train.mean(axis=0)                            #求每一列特征的平均值
std_on_training = X_train.std(axis=0)                              #求每一列特征的标准差

#training_scale数据集中的特征列均值为0，标准差为1
X_training_scale = (X_train-mean_on_training)/std_on_training        #数据集减去每个特征的均值。再除以标准差
X_test_scale = (X_test-mean_on_training)/std_on_training             #同样地对测试集数据进行测试

mlp = MLPClassifier(random_state=42, alpha=1)                        #加载神经网络模型, 增加alpha到 1
mlp.fit(X_training_scale, y_train)                                   #训练数据集

print('Accuracy on training set:{}'.format(mlp.score(X_training_scale, y_train)))             #输出训练集预测准确度
print('Accuracy on test set:{}'.format(mlp.score(X_test_scale, y_test)))                      #输出测试集预测准确度

Accuracy on training set:0.9859154929577465
Accuracy on test set:0.9790209790209791

此时，该神经网络的预测准确度达到了97.9%，表现十分不错。

分析特征的权重

虽然可以分析神经网络学到了什么，但这通常比分析线性模型或基于树的模型更为复杂。

要想观察模型学到了什么，一种方法是查看模型的权重。

import matplotlib.pyplot as plt
plt.figure(figsize=(20,5))                                               #显示面板
plt.imshow(mlp.coefs_[0], interpolation='none', cmap='viridis')
plt.yticks(range(30), cancer.feature_names)
plt.xlabel('Columns in weight matrix')
plt.ylabel('Input feature')
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x1d647d30588>

可以推断，如果某个特征对所有隐单元的权值都很小，可以认为该特征对模型来说"不太重要"，反之亦然。

优、缺点和参数

神经网络模型的优点之一是能够获得大量数据中包含的信息，并构建无比复杂的模型。

但是通常需要仔细地进行数据预处理，并调节相关参数。