文章信息

题目： Density?based weighting for imbalanced regression
期刊：Machine Learning
作者：Michael Steininger 1， Andreas Hotho 1，Konstantin Kobs 1 · Padraig Davidson 1 · Anna Krause 1 ·

背景

相比于分类场景，回归场景的不平衡问题是一个被忽视的方向。不平衡问题的解决的方法大致有两类：
（1）Data level：通过上采样/下采样想办法把数据的分布变平衡;
（2）Algorithm level：通过设计算法/模型来克服因数据不平衡而导致的模型预测Bias；
这篇文章的目的也是解决不平衡回归问题。

动机

当前有少部分解决不平衡回归的文章，这些文章大都采用Data level的方法。然而分类场景中Algorithm level的方法相比Data level的方法有很大优势。因此，本文试图提出一种Algorithm level的方法来解决不平衡回归问题。具体来说，首先基于核密度估计(KDE)提出一种样本加权的方法用于给不同的样本指定权重，然后与经典的代价敏感学习Cost-sensitive learning的思路结合，提出了一种新的损失函数DenseLoss。

方法

方法非常的简单，先介绍所谓的样本加权DenseWeight。

DenseWeight

所谓的DenseWeight顾名思义就是根据密度来指定样本的权重。那么怎么来指定权重呢？实际上就是根据样本目标值y的稀有程度/密度来指定权重，密度越大，则相应的权重小一点。

开始之前，作者首先指出了权重应该满足的一些属性，然后基于这些属性要求来设计Loss。
权重的一般属性：
（1）样本的目标值y的密度越大，则其权重应该越小；
（2）希望有一个超参数 $\alpha$ 能够控制加权的程度： $\alpha=0$ 时，对应均匀分布，即样本的权重权重全部为1， $\alpha$ 越大，则加权的程度越大；
（3）样本的权重权重为正值以避免有的样本被忽视;
（4）所有样本权重的均值应当为1，这一点学优化时的补偿有关，以避免影响学习率；

接下来，DenseWeight的具体步骤：
假设有N个样本，第i个样本的目标为 $y_{i}$ ,
Step 1: 基于核密度估计KDE来估算每个样本的密度，对于样本x，其密度的估计公式如下，
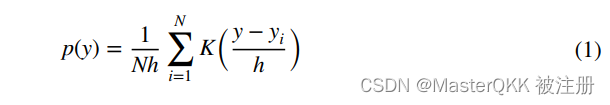
在这里插入图片描述
注： KDE是一种经典的非参数密度估计方法；
Step 2：将所有样本的密度归一化到(0，1)之间

Step 3:设置样本的初始权重

可以看到密度越大，权重越小，并且参数 $\alpha$ 可以控制加权的程度，Step 2实际上是为了使Step 3的权重指定规则有意义；
Step 4：通过截断使每个样本的权重都为正
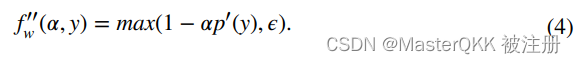
在这里插入图片描述
这一步使为了满足属性（3）；
Step 5：归一化

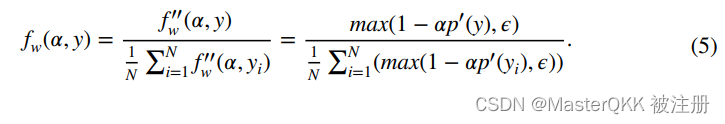
这一步是为了满足属性（4）；

DenseLoss

DenseLoss的思想实际上就是代价敏感学习，具体到这儿，就是通过上一节的DenseWeight把密度低的样本的Loss放大，把密度大的样本的Loss缩小来客服不平衡问题。故，Loss的定义如下：
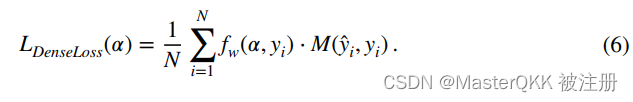
在这里插入图片描述
其中M表示损失的计算函数。OK。
这里可以发现：
（1）当 $\alpha=0$ 时，所有样本的权重为1，退化成了原始的损失；
（2） $\alpha$ 值越大，则权重的设置对密度越敏感，密度大的样本的权重越远离1；