[人工智能]【论文学习】MKIoU Loss: Towards Accurate Oriented Object Detection in Aerial Images

【论文学习】MKIoU Loss: Towards Accurate Oriented Object Detection in Aerial Images

在本文中，提出了一种近似 SkewIoU 的调制卡尔曼 IoU 损失，命名为 MKIoU。以往的高斯分布建模的方法会有类正方形的问题，所以，提出了高斯角损失（GA Loss）来解决这个问题。

论文链接：MKIoU Loss: Towards Accurate Oriented Object Detection in Aerial Images

一、前言

在本文中，作者提出了一种更精确的调制卡尔曼 IoU 近似 SkewIoU 用于定向目标检测，称为 MKIoU。通过分析，发现回归不准确是由于预测框与真实框接近时损失变化趋势不敏感，即损失与度量不一致。因此，充分考虑角度偏差和宽高偏移对损耗变化的敏感性，提出了一种调制方法，使损耗与评估指标更加一致。此外，高斯建模方法无法学习类正方形目标的角度信息，如图 1 所示，这影响了模型的高精度检测性能。因此，提出了一种 GA Loss，它可以纠正方形物体的角度混淆，如图 1 所示。此外，它可以很容易地添加到其他高斯建模方法中。本文的亮点可概括如下：

• 提出了一种更准确的调制卡尔曼 IoU 损失，命名为 MKIoU，它更关注损失趋势与评估指标的一致性。与 KFIoU 相比，本文的方法实现了更高的准确度。
• 提出了一种高斯角度损失，以克服高斯建模方法对类正方形物体的角度混淆问题，从而进一步提高高精度检测的性能。

图1：基于高斯的损失和添加高斯角损失的检测结果的可视化

二、相关工作

三、方法

作者先分析了 KFIoU Loss 的不足之处。然后在KFIoU的基础上提出了一种调制的Kalman IoU loss，更加关注角度偏差和宽高偏移对loss变化的敏感性。此外，为了克服高斯建模方法引起的方形目标角度混淆问题，提出了高斯角度损失。

3.1 调制的Kalman IoU loss

先回顾了一下KFIoU的工作，具体内容可参考：KFIoU。这里直接把KFIoU的相关公式放过来：

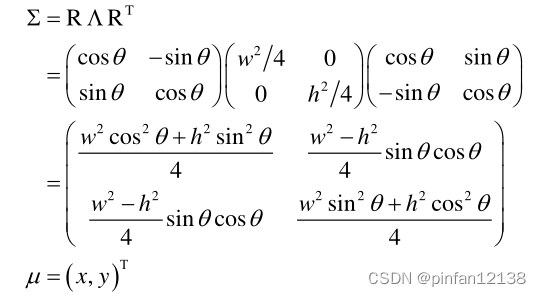
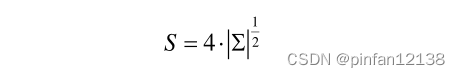
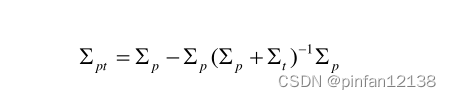
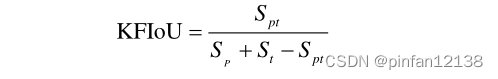
其中，$\Sigma$和$\mu$分别是将旋转框转化为高斯表征后对应高斯分布的协方差矩阵和中心点坐标。$S$是利用协方差计算的旋转框面积。${\Sigma }_{pt}$是预测框和真实框对应的高斯分布（椭圆）在中心重合后相交部分近似椭圆的协方差。
本文作者经过分析发现：KFIoU 损失在精度更高的指标（AP75和AP50：95）中的结果不好，即回归结果不准确。通过联立上面的方程，得到：


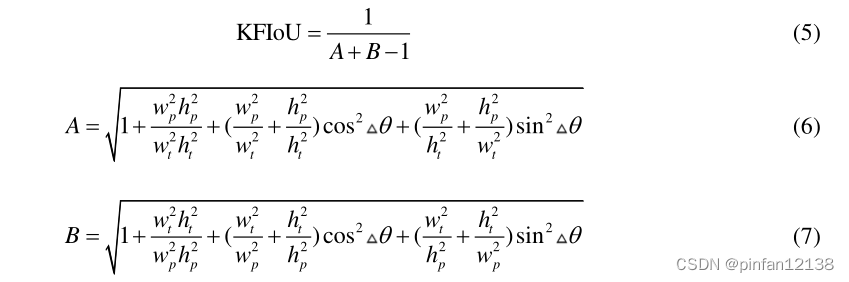
经过联立方程，KFIoU可以化简成（5）式的形式，其中A和B两部分分别如上，经过分析发现$A+B\ge 4$，当满足（8）中条件之一时等号成立。
也就是说，当预测框和真实框完全重叠时，KFIoU取最大值的1/3。为了方便与SkewIoU进行比较，将KFIoU乘以3，使得取值范围为[0,1]。经过图2的可视化分析，可以发现：KFIoU（红色）的变化趋势与SkewIoU（蓝色）的实际趋势存在显着差异。具体来说，当预测框接近真实框时，KFIoU远大于实际IoU，这使得模型的优化变得不敏感，从而损害了模型的高精度检测性能。

我们希望近似 IoU 的变化趋势与 SkewIoU 一致。因此，作者提出了 MKIoU，它通过调制因子 α 进行调整：

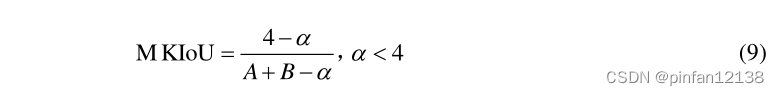
MKIoU的取值范围是(0,1]。KFIoU是MKIoU的一个特例，当α=1时，MKIoU等于3倍的KFIoU。图2(a)显示了当两个bounding box中心和角度相同时，α值不同的MKIoU随着高宽偏移的变化。可以看出，当α=1时，MKIoU对宽高偏移的敏感度远低于SkewIoU，导致结果不准确。 α增加，灵敏度逐渐增加，使得MKIoU的趋势与评价指标更加一致。图2（b）显示了当两个边界框具有相同的中心、宽度和高度时，MKIoU的角度偏差的灵敏度。注意随着物体高宽比的增加，SkewIoU对角度的敏感度增加，很小的角度变化也会引起SkewIoU的急剧变化，不利于损失函数的一个稳定且准确的回归。因此，α 不是越大越好，最终的α值是通过对比实验确定的。

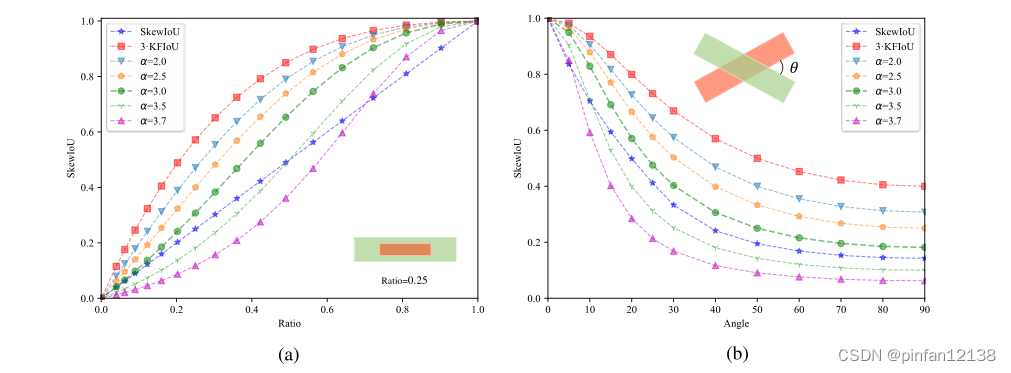
图2：不同条件下MKIoU曲线对比

3.2 高斯角度损失

基于高斯的方法有效地避免了边界问题，但是当对象是正方形时，即 $w=h$ ，其二维高斯分布是一个不能准确表示方向的圆。在类正方形情况下，缺少角度信息会导致物体的角度混乱，从而影响高精度检测的性能。图 1（上）显示了角度混淆问题的可视化。为了解决这个问题，作者提出了高斯角度损失，可以表示为：


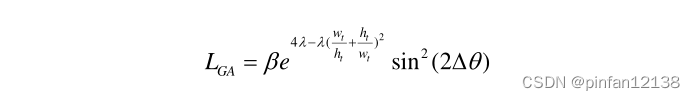
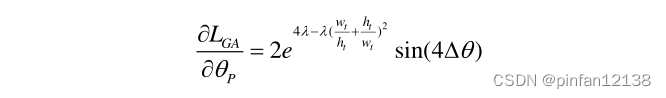
其中$\beta$和$\lambda$是超参数，文中$\lambda$设为3，$△\theta ={\theta }_p?{\theta }_t$，${\theta }_p$的修正只与ground-truth的角度偏差和高宽比有关。在正方形情况下，即$w_t=h_t$时，损失关于角度的偏导为$?L_{GA}/?{\theta }_p=2\sin (4△\theta )$，这意味着随着ground-truth的高宽比接近1，角度梯度会呈现$90^{°}$的周期性变化，这与正方形的角周期是一致的。随着高宽比的增加，$?L_{GA}/?{\theta }_p$会逐渐趋近于0，GA损失将失效。详情看图3。 GA Loss 可以很容易地在 MKIoU 上实现，并且很容易添加到其他高斯建模方法中，提高了高精度检测的性能。

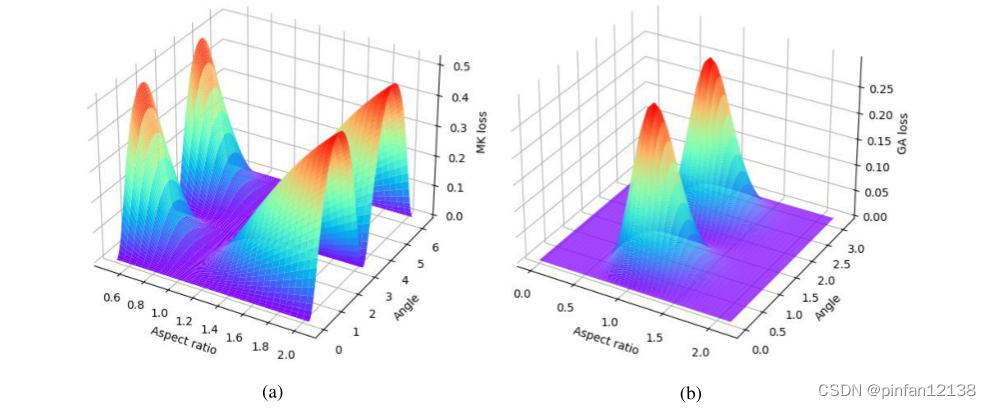
图3：Loss（Z 轴）、高宽比（X 轴）和角度偏差（Y 轴）之间的关系。 MK Loss (a) 随着角度偏差的变化周期性地变化 180°。高宽比越大，损失越大，说明模型更注重优化高宽比较大的对象。然而，随着高宽比接近 1，MK Loss 接近 0，并且没有梯度变化。当高宽比接近1时，GA Loss (b)随着角度偏差的变化周期性变化90°。随着高宽比变大，损失接近0，因此不影响原始损失值

3.3 损失函数

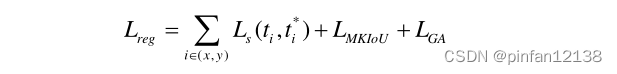
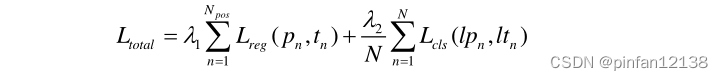
其中$L_s$是Smooth L1 Loss，$L_{MKIoU}=1?MKIoU$，$L_{GA}$是高斯角度损失，$L_{total}$是全局损失，${\lambda }_1$和${\lambda }_2$是超参数，文中设为{0.01,1}。

四、实验

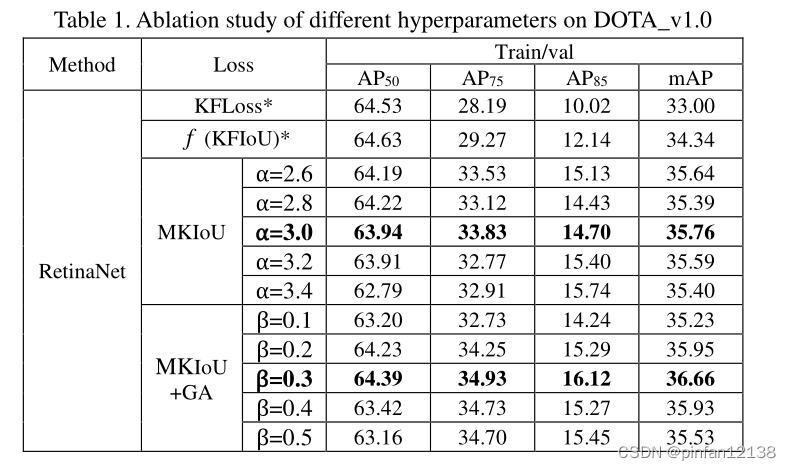
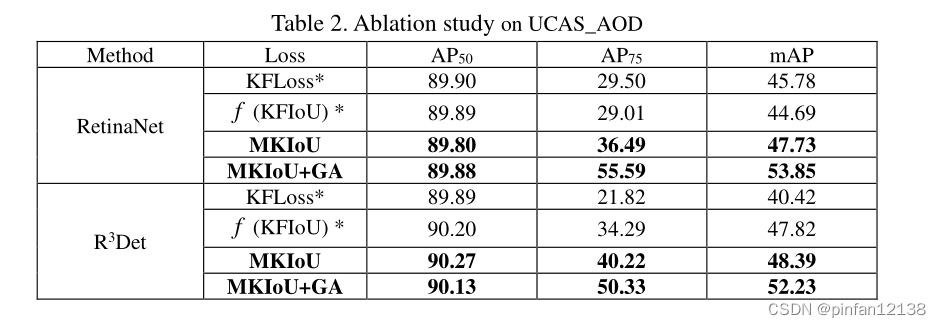
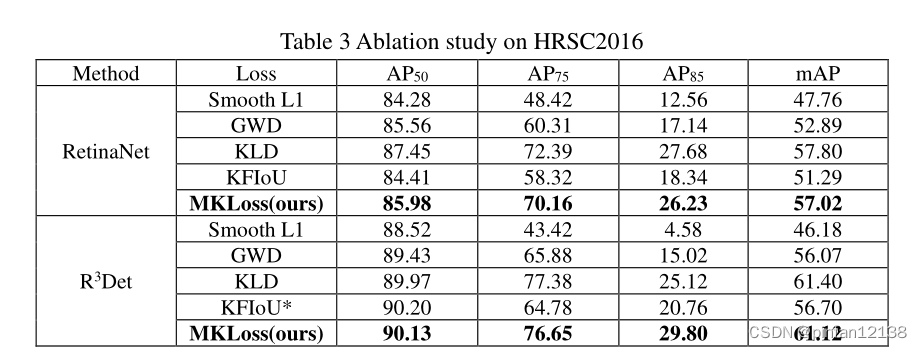
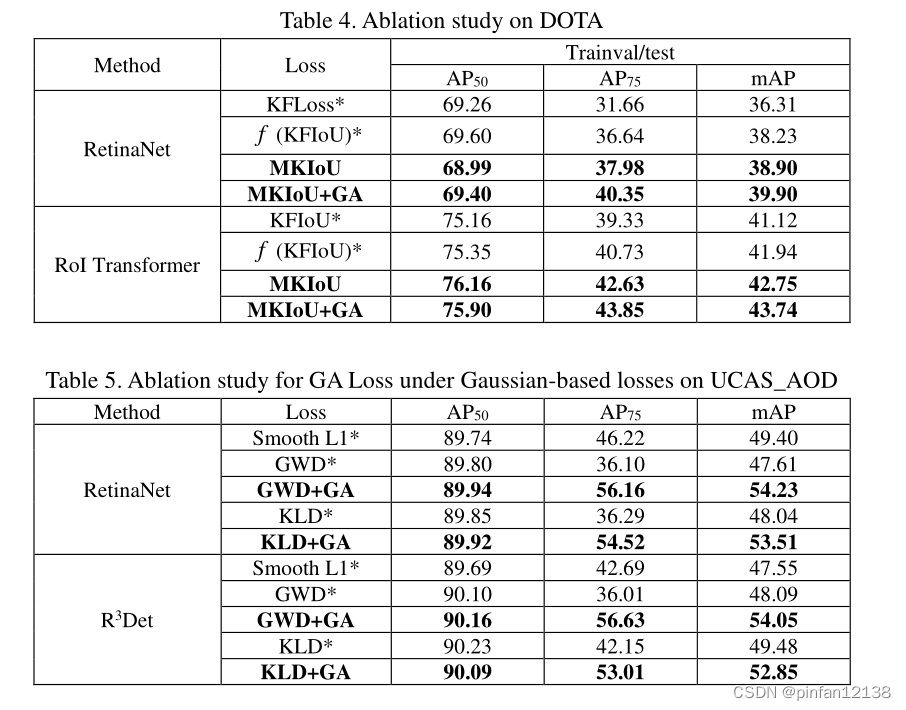
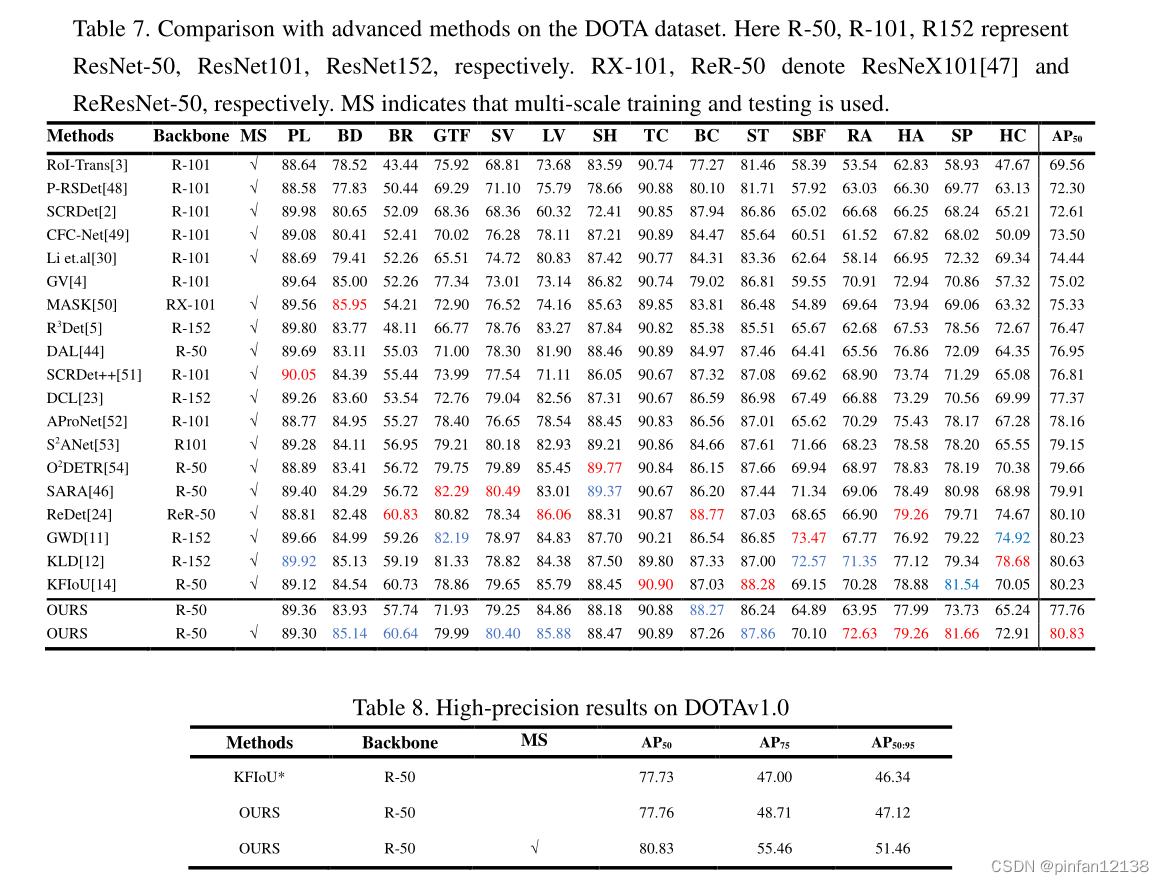
可以看到MKIoU可以达到与KFIoU相当的成绩，并且在$A{P}_{75}$$A{P}_{50?95}$这两个指标上实现了可观的提升。

五、结论

在本文中，作者提出了一种用于定向目标检测的近似 SkewIoU 的调制卡尔曼 IoU 损失，称为 MKIoU 损失。与KFIoU相比，MKIoU更加关注宽高偏移和角度偏差对loss变化的敏感性，从而显着提升了模型的高精度检测性能。此外，为了克服高斯建模方法中方形物体的角度混淆问题，提出了高斯角度损失。在几个公共数据集上进行的实验证明了我们方法的有效性，并取得了与最先进方法相当的结果。虽然文中方法实现了更准确的检测，但仍然存在一些缺点，例如错误分类和检测具有巨大高宽比的对象。因此，在未来的工作中，将专注于有效减少错误分类并提高具有巨大纵横比的物体的精度。

本文主要创新有两个点：
1.在KFIoU的基础上，提出了新的高斯损失MKIoU，通过数学上的分析指出了KFIoU的不足并提出了自己的解决方法，将着重点放在Loss对参数变化的灵敏度与SkewIoU对参数变化灵敏度的近似上。
2.针对高斯分布损失的类正方形提出了一个新的损失函数GA Loss，这是容易实现的，而且GA Loss具有高宽比为1时损失最大，高宽比增大时损失迅速衰减的特性，避免了对非正方形物体的影响。
本文没有公开代码，但所有实验都是在mmrotate上实现的，复现难度不高。