主流序列转录模型( sequence transduction models )是基于复杂的循环和卷积神经网络，通常是用编码器-解码器（ encoder-decoder ）架构。性能最好的模型通常也会在编码器-解码器之间使用注意力机制。文章提出了一个简单的新架构 Transformer -- 仅仅依赖于注意力机制，不使用循环和卷积。在两个机器翻译任务上展示了特别好的性能--更好的并行度，训练时间更短。在 WMT 2014 Englishto-German 翻译任务上达到了28.4的 BLUE score，比目前最好的结果提升了2个 BLUE （包括集成模型）。在 WMT 2014 English-to-French 翻译任务中，做了一个单模型，效果优于其他的单模型，在8个? GPU 上训练了3.5天达到了41.8的 BLUE ，其训练时间相对于文献中其他模型的训练时间来说很少。 Transformer 架构能够很好的泛化到其他任务。

导言

在RNN里面是把序列从左往右一步一步的往前计算。假设序列是一个句子，他就是一个词一个词的往前看，对 t 个词会计算一个输出（隐藏状态）? $h_{t}$ ?，其是由前一个时刻的隐藏状态? $h_{t-1}$ ?和当前? $t$ ?时刻的输入决定的。它是一个时序即一步一步的计算过程，难以并行。如果序列比较长的话，很早期的那些时序信息在后面的时候可能会丢掉，若不想丢掉，会需要比较大的? $h_{t}$ ?，但是每一个时间步的? $h_{t}$ ?都得存下来，会导致内存开销比较大。

已经有相关工作将 attention 应用到了编码器-解码器里面了，主要是用于如何将编码器的东西有效的传给解码器，即和 RNN 是一起使用的。

背景

卷积网络替换循环神经网络来减少时序的计算。但是卷积神经网络难以建模长序列，因为卷积计算每次去看一个比较小的窗口（例如一个3*3的像素块），若两个像素隔得比较远，得用很多层卷积，一层一层堆上去才能把隔的较远的像素融合起来。但是使用 Transformer 里面的注意力机制，每次能看到所有的像素，一层就能看到整个序列。但是卷积可以有多输出通道，每一个输出通道可以认为是识别不一样的模式，想要获得类似多输出通道的效果，提出了多头的注意力机制（ Multi-Head Attention ）。

自注意力机制（ self-attention ）将单个序列的不同位置联系起来以计算序列的表示，之前的有些工作已经使用了自注意力机制。

基于循环 attention 机制的端到端的 memory networks ，而不是序列对齐的循环，在简单语言中的问答和语言建模任务中表现良好。

Transformer 是第一个仅依赖于自注意力机制来做的编码器-解码器框架。

模型架构

编码器将序列的符号表示? $x=(x_{1}, x_{2}, \cdots ,x_{n})$ ?映射成相同长度的序列的向量表示? $z = (z_{1}, z_{2}, \cdots , z_{n})$ ? 。对于句子来说，? $x_{t}$ ?可以看作是句子中第 t 个词在词表中的下标， $z_{t}$ ?代表? $x_{t}$ ?的向量表示， n 表示序列的长度。给定编码器的输出? $z$ ?，解码器会生成长为 m 的序列? $y = (y_{1}, y_{2}, \cdots , y_{m})$ ?，这里的 n 可以不等于 m 。解码器的词是一个一个生成的（自回归，例如生成? $y_{t}$ ?，可以拿到编码器输出 $z$ 和 t 时刻前的解码器的输出? $(y_{1}, y_{2}, \cdots , y_{t-1})$ ?，过去时刻的输出会作为当前时刻的输入），这一点与编码器不同，编码器一次很可能能看完整个句子。

Transformer 使用了一个编码器解码器的架构，将 self-attention 、 point-wise 、 fully connecte layers 堆叠在一起的。

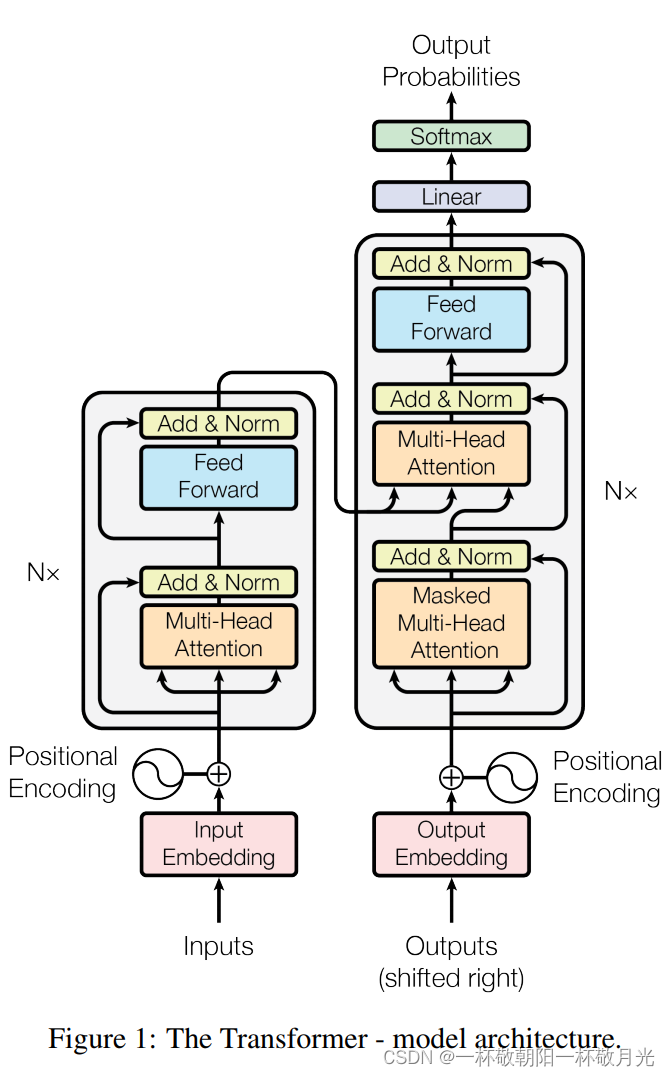
编码器的输入：例如中译英，就是中文的句子。解码器的输入：解码器在做预测的时候是没有输入的，实际上解码器之前时刻的一些输出作为输入。（ shifted right 一个一个往右移）。

编码器解码器堆叠

编码器：由? $N=6$ ?个完全一样的层（ layers ）堆叠起来。每一个层里面有两个子层（ sub-layers ）。第一个子层是多头自注意力子层（ multi-head self-attention mechanism ），第二个子层是一个全连接层（就是一个MLP）。每一个子层都用了一个残差连接，再接上 layer normalization 。每个子层的输出用式子可表示为? $LayerNorm(x + Sublayer(x))$ ?。因为残差网络需要输入 x 和子层的输出? $Sublayer(x)$ ?的维度是一样的，否则得做投影，简单起见，将 embedding 层和所有子层的输出维度统一为? $d_{model} = 512$ ?。

解码器：解码器也是由6个完全一样的层堆叠起来的。解码器有3个子层。第一个子层是 masked multi-head self-attention?，因为解码器做的是一个自回归（当前输出的输入集是上面一些时刻的输出），即预测的时候我们不应该看到之后那些时刻的输出（保证训练和预测的行为的一致性），但是在注意力机制中每次都能看到完整的输入，解码器训练的时候，预测?t 时刻的输出不应该看到 t 时刻以后的那些输入，可以通过带掩码的注意力机制实现。第二个子层是 multi-head? attention ，其中 k ， v 来自编码器的输出， q 来自解码器的前一子层的输出，这边不需要掩码，因为在翻译任务中，我们是能拿到完整的源语言的句子的，上一子层的 mask 是针对目标语言的，我们翻译的时候都是逐字逐词从前往后翻的。第三个子层同编码器第二个子层一样是一个全连接层。每一个子层都用了一个残差连接，再接上 layer normalization 。

注意力层

注意力函数是将一个 query 和一些 key-value 对映射成输出的一个函数， query ， keys ， values? 和 output 都是一些向量， output 是 values 的加权和（在最后一维的长度上，输出和 values 是一样的），每一个 value 的权重是其对应的 key 和 query 的相似度（ compatibility function ，不同的注意力机制有不同的算法）算出的。

Scaled Dot-Product Attentions

queries 和 keys 维度相同都是? $d_{k}$ ?， values 的维度是? $d_{v}$ ?，将 query 和所有的 keys 做内积作为相似度，得到的结果再除以? $\sqrt{d_{k}}$ ?，再用一个 softmax 来得到最后的权重（ attention scores ）。

实现时，将 queries 拼成一个矩阵? $Q$ ?， keys 和 values 也一起组合成矩阵?K?和?V?。则输出矩阵为：

$Attention(Q,K,V) = softmax(\frac{QK^{T}}{\sqrt{d_{k}}}) V \ \ \ (1)$

有两种常见的注意力机制，一种是加性注意力机制（ additive attention ，用一个隐藏层的全连接层实现，可以处理 query 和 key 不等长的情况），另一种是点积注意力机制（ dot-product? ( multiplicative )? attention，这边在传统点积的基础上除以了? $\sqrt{d_{k}}$ ?），这两种都差不多，但是点积实现比较简单，且比较高效，两次矩阵乘法就能搞定。当? $d_{k}$ ?的值比较小的时候，这两个机制的性能相近，当? $d_{k}$ ?比较大时，加性注意力机制比不带缩放的点积注意力机制性能好。

除以了? $\sqrt{d_{k}}$ ?的解释：

我们怀疑，对于长度比较大的向量，点积绝对值有可能很大，也可能比较小，相对的差距就会变大，套上 softmax 函数最大的那个值会更加接近1，剩下的值更加接近0，值更加向两端靠拢，计算梯度的时候会发现梯度比较小，因为 softmax 最后的结果是希望预测的值置信的靠近1，不置信的地方尽量接近0，这样就可以说收敛的差不多了，这时候梯度就比较小，就跑不动。

假设 q 和 k 的分量是均值为0、方差为1的独立随机变量，它们的点积

$q \cdot k = \sum_{i=1}^{d_{k}}q_{i}k_{i}$ 是均值为0，方差为? $d_{k}$

$E(XY) = E(X)E(Y)$

$D(XY)=E[(XY - E(XY))^{2}] = E[X^{2}Y^{2} -2XYE(XY)^{2} + (E(XY))^{2}] =E(X^{2}Y^{2}) - 2E(X)E(Y)E(XY)^{2}+ (E(XY))^{2} =E(X^{2})E(Y^{2})-E(X)^{2}E(Y)^{2}=[D(X)+E(X)^{2}][D(Y)+E(Y)^{2}]==[D(X)D(Y)+D(Y)E(X)^{2}+D(X)E(Y)^{2}]=1$

则? $d_{k}$ ?个相加就是均值0，方差? $d_{k}$ ?，这个是时候若除以? $\sqrt{d_{k}}$ ?，则就又会变为均值0方差1。

transformer 里面? $d_{k}$ ?一般比较大，通常是512，为了抵消这种影响，我们通过除以? $\sqrt{d_{k}}$ ?将点积幅度缩小。

mask 主要是为了避免在第 t 时刻看到之后时间的东西，假设 query 和 key 是等长的，长度为 n ，且在时间上是能对应起来的，那么第 t 时间的 queries? $q_{t}$ ?，那么在计算的时候应该只去看 keys 的? $k_{1}, k_{2}, \cdots , k_{t - 1}$ ?，而不应该去看? $k_{t}$ ?和它之后的东西，因为在当前时刻还没有? $k_{t}$ ?，但是注意力机制会看到所有， $q_{t}$ ?会和 keys 里面所有的 k 做运算（即会和? $k_{1}, k_{2}, \cdots , k_{t - 1}, k_{t}, \cdots , k_{n}$ ?计算），其实是可以全部计算的，只要保证在计算权重的时候不要用到后面这些东西，所以就有图2中的 mask ，对于? $q_{t}$ ?与 $k_{t}$ ?及之后的那些计算值替换成一个非常大的负数，例如? $-1e^{10}$ ?，这么大的负数在经过 softmax 后就会变成0，所以 softmax 之后? $k_{t}, \cdots , k_{n}$ ?对应的那些权重都会变成0，那么起作用的就剩下? $k_{1}, k_{2}, \cdots , k_{t - 1}$ ?，相当于在计算 output 的时候只用了 values 的 $v_{1}, v_{2}, \cdots , v_{t - 1}$ ?，后面的那些没有看，所以mask的作用是训练的时候让第t个时刻的 query 只看对应的前面那一些的 key-values 的 pair 对，使预测的时候能跟训练的时候一一对应上的。

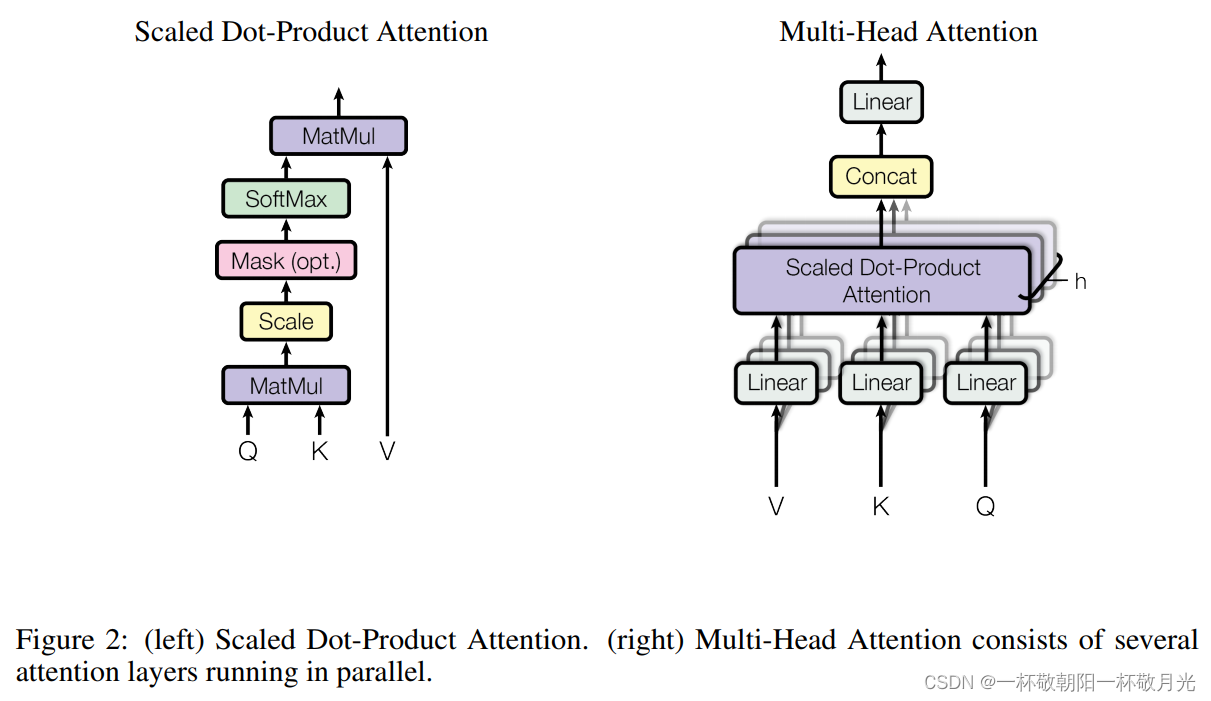
Multi-Head Attention

与其做一个单个的注意力函数，不如将整个 queries ， keys ， values 投影到一个低维的空间投影? h 次，再做 h 次的注意力函数，将每一个函数的输出并在一起再投影回来得到我们最终的输出，见图2。 Scaled Dot-Product Attentio 里面没有可学的参数，注意力函数就是内积，有时候为了识别不一样的模式，希望可以有一些不一样的计算相似度的方法，若用加性注意力机制还是有权重可以学的，Multi-Head Attention 先投影到一个低维空间，这个投影的 W 是可以学的，给 h 次机会希望可以学到不一样的方法，使得在投影进去的那个度量空间能匹配不同模式需要的一些相似函数，最后再投影回来（有点像卷积里面多输出通道的感觉）。

$MultiHead(Q,K,V) = Concat(head_{1}, \cdots, head_{h})W^{O} \ \ \ (2)$

其中，

$head_{i} = Attention(QW^{Q}_{i}, KW^{K}_{i}, VW^{V}_{i}) \ \ \ (3)$

投影矩阵的维度

$W_{i}^{Q} \in \mathbb{R}^{d_{model} \times d_{k}}, W_{i}^{K} \in \mathbb{R}^{d_{model} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{model} \times d_{v}}$

我们采用? $h=8$ ?个并行的注意力层，或者说 heads ，则各个维度是? $d_{k} = d_{v} = d_{model} / h = 64$ ? 。由于每个 head 的维数减少，总计算成本与全维单头部注意力的计算成本相似。虽然我们看到式（3）有许多小矩阵的乘法，实际上也可以通过一次的矩阵乘法来实现。这边贴一个哈佛大学的pytorch版本的实现， The Annotated Transformer，先做一个不改变维度的投影，Q 、 K 、 V 是三个不同的投影矩阵，且投影矩阵的形状均是是? $W \in \mathbb{R} ^{(d_{model}, d_{model})}$ ?，通过一个输入输出均是? $d_{model}$ ?的线性层实现，将得到的矩阵变成我们要的形状，先 reshape 将最后一维切成? $(head, d_{k})$ ?，再 transpose 因为我们希望得到的最后两维是序列长度和 embedding 维度? $(seq\_len, d_{k})$ ? 。?


def clones(module, N):
    "Produce N identical layers."
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

linears = clones(nn.Linear(d_model, d_model), 4)
query, key, value = [
    lin(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
    for lin, x in zip(linears, (query, key, value))
]

transformer 中的注意力机制三种使用姿势

编码器中的自注意力机制，设batch_size=1，句子长度n， embedding 维度? $d_{model}$ ?，则它的输入是形状为? $(1, n, d_{model})$ ?的向量（ n 个长度为? $d_{model}$ ?的向量），注意力层的三个输入（ queries ,? keys , values ）是一根线过去的然后 copy 三次，即?queries , keys , values 是同一个东西，这就是自注意力机制，n 个 queries ，每一个 query 会得到一个输出（ values 的加权和，权重是? query 和对应的 keys? 的相似度），则有 n 个输出，输出的最后一维的长度和 values 最后一维的长度一样也是 $d_{model}$ ，即输入输出的形状一样。由于多头会学习出 h 个不同的距离空间。

解码器中的自注意力机制，和编码器类似，可能就是长度变成 m ，embedding 维度也是? $d_{model}$ ?。有区别的是编码器有 mask ，当算 t 时刻的 query 对应的输出，不应该看到 t 时刻之后的东西，t 时刻之后的权重要设置为0（赋一个大负数，这样过 softmax 后就是0啦，即只有 t 时刻前的起作用（不包括 t 时刻））。

编码器解码器之间的注意力机制，这边不再是自注意力了， keys 和 values 来自编码器最后一层的输出（形状是 $(1, n, d_{model})$ ?），queries 是来自解码器前一层的输出（形状是 $(1, m, d_{model})$ ?）。意味着对解码器的每一个 query 要算一个输出（来自编码器输出的 values 的加权和），可以理解为将编码器的输出根据解码器的输出拎出来。

Position-wise Feed-Forward Networks

他就是一个 MLP ，这边有一个 Position-wise ， position 输入序列有很多个词，一个词就是一个点 position ，把一个 MLP 对每一个词作用一次（对每一个词作用的是同样一个 MLP ），就是 MLP 作用在最后一个维度（每一个词共享同一个权重参数矩阵），它的另一种描述方式是两个kernel大小为1的卷积。

$FFN(x) = max(0, x W_{1} + b_{1}) W_{2} + b_{2}$

有两个线性层，第一个线性层的输出维度是? $d_{ff} = 2048$ ?，将维度扩大了4倍，最后有一个残差连接，为了保证维度不变，所以第二层将维度投影回? $d_{model}$ ?。

解释，关于transformer怎么有效的使用序列信息。

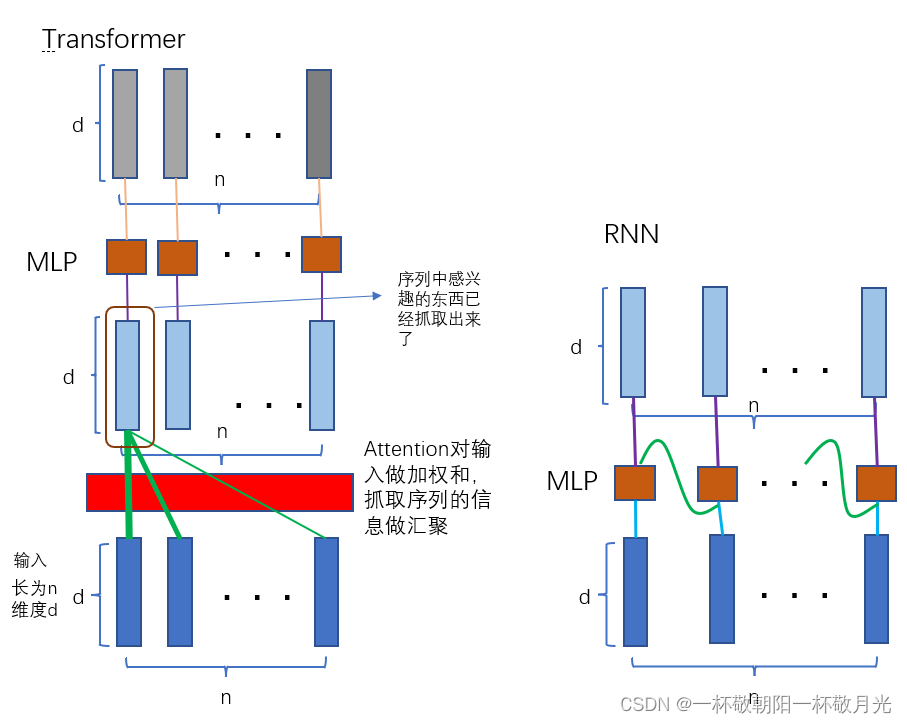
考虑简单情况，无残差连接，也没有 layerNorm ，然后 attention 是一个单头的。在 transformer 的 MLP 虽然画了多个棕色的框，但是其实是一个它们的权重是一样的，每个 MLP 对你每一个输入的点做运算，会得到一个输出。输入和输出的大小都是一样的， attention 的作用就是把整个序列里面的信息抓取出来做一次汇聚 aggregation ，所以序列中我们感兴趣的信息就已经抓取出来了，以至于在做投影（ MLP ）映射成我们更想要的语意空间的时候，因为已经涵盖了我们要的序列信息，所以每个 MLP 只要在对每个点独立做就行。因为序列信息已经被汇聚完成，所以 MLP 是可以分开做的。这就是transformer 如何抽取序列信息然后把这些信息加工成我们最后要的语意空间的向量的过程。

RNN，棕色的 MLP 也是每个时间步共享权重矩阵。如绿色的线表示把上一时刻的输出（作为历史信息）放回来和该时刻的输入一起并进去（就完成了信息的传递），得到当前时刻的输出。

RNN 和 Transformer 一样都是用一个 MLP 来做语意空间的转换，不同的是传递序列信息的方式， RNN 是把上一时刻的信息输出传入到下一时刻做输入，?Transformer 是通过一个 attention 层去全局的抓取整个序列里面的信息，然后再用 MLP 做语义的转换。关注点都是如何有效的使用序列信息。

Embeddings and Softmax

对于任何一个词学习长为? $d_{model}$ ?的向量表示它，编码器、解码器以及 softmax 前的线性均需要 embedding ，这三者是一样的权重，权重乘上了? $\sqrt{d_{model}}$ ?。

解释：为啥要乘上? $\sqrt{d_{model}}$ ?，为了后面加上位置编码的时候，能在同一个 scale 上不被淹没，参照 transformer encoder输入单词,对单词进行embedding的时候，为什么乘根号d？？ - 知乎?@王四喜和 @Quokka?。

因为是3个 embedding 层共享权重的，其中有?softmax 前的线性层，通常是要用?xavier 等方法初始化的，也即编码器、解码器的 embedding 亦是如此。xavier?初始化的? $W\sim N(0, 1/n)$ ?，这边的? $n = d_{model}$ ?，即? $Embedding \sim N(0, 1/ d_{model})$ ?，维度比较大的时候学的权重值就会变小，但是之后要加位置编码，所以想把? $Embedding \sim N(0, 1)$ ?，这样相加的时候就在同一个 scale 上。

Positional Encoding

attention 是没有时序信息的，输出是 values 的加权和，权重是 query 和 keys 的相似度，和序列信息无关，不会关注 key-value 对在序列的什么位置，换句话说，给定一句话，将词打乱 attention 的结果是一样的（最多顺序发生了变化），尽管词在序列中的顺序发生了变化，但是加权和不会变，这是不合理的，词序打乱可能会影响语义，所以需要通过别的方式加入时序信息。 RNN 是上一时刻的输出作为下一时刻的输入来传递历史信息，其本来就是带时序的。在输入中添加时序信息，例如一个词在位置 i ，将位置? $(1,2,\cdots , max\_len)$ ?加入到输入里面。

$\begin{matrix} PE_{(pos, 2i)} &= \sin(pos / 10000^{2i/d_{model}}) \\ PE_{(pos, 2i + 1)} &= \cos(pos / 10000^{2i/d_{model}}) \end{matrix}$

思路：在计算机中假设用32位的整数表示数字，就是说用32个 bit ，每个 bit 上有不同的值来表示? $0,1,2,...$ ??，可以认为一个数字使用一个长为32的向量表示的。现在，词会被表示成一个维度为? $d_{model}$ ??的向量，同样这里我们用? $d_{model}$ ? 的向量表示数字，具体的值是通过周期不一样的 sin 和 cos 函数来算出来的。

其中pos?是位置，i?是维度。也就是说，位置编码的每个维度对应于一个正弦曲线。这些波长的范围是? $[2*\pi ,10000 * 2 * \pi]$ ，准确来说范围是? $[2 * 1* \pi, 2 * (d_{model} - 2)/ d_{model} * \pi]$ ?。我们选择这个函数是因为我们假设它允许模型很容易通过相对位置来学习到相对位置信息，因为对任意确定的偏移k,? $PE_{pos+k}$ ?可以表示为 $PE_{pos}$ ?的线性函数。

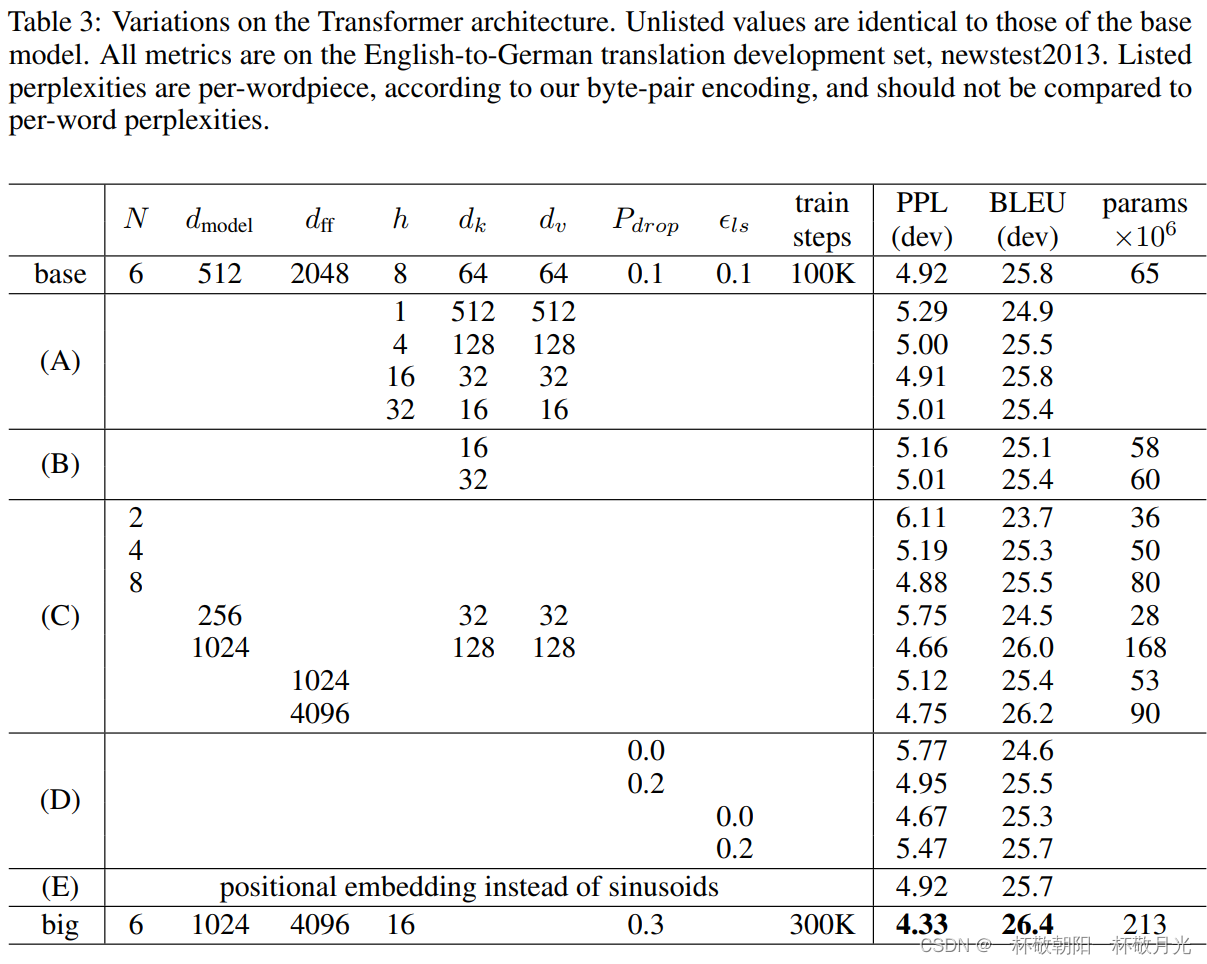
还使用可训练的位置embeddings进行了试验，发现这两个版本产生几乎相同的结果（参见表?3 的 E 行）。选择正弦曲线，因为它可以允许模型推断比训练期间遇到的更长的序列。

下图中，? $d_{model} = 512$ ?，这边序列长度取了100，在 embedding 维度上切? $[70, 73]$ ?时的位置编码，固定住i，即最后一维，只看其值随位置的变化则是一个个不同周期的正弦（偶）或余弦函数（奇），波长随着 i 的增大而增大。

plt.figure(figsize=(15, 5))
# 词嵌入维度512， 置0比率为0
pe = PositionalEncoding(512, 0.)
# 向pe中传入一个全零初始化的x，相当于展示pe, [bs, seq_len, d_model]
y = pe(torch.zeros(1, 100, 512))
for dim in range(70, 74):
    plt.plot(np.arange(100), y[0, :, dim].data.numpy())
    
plt.legend(['dim {}'.format(p) for p in range(70, 74)])
plt.show()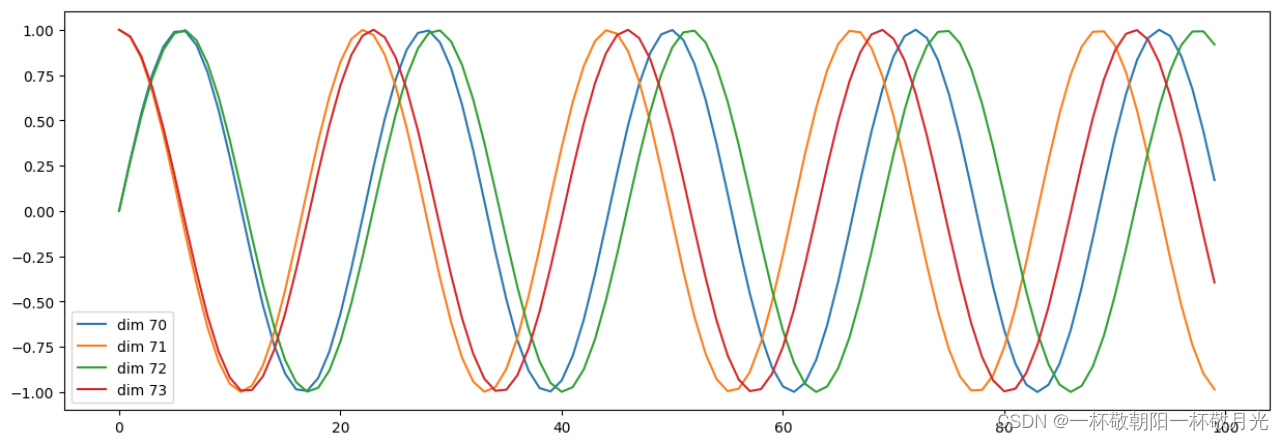

Why Self-Attention

表1比较了四种不一样的层，比较了三个方面，复杂度，计算的顺序性（这个越少越好，表示下一步计算必须等前面多少步计算完成），最大的长度（表示信息从一个数据点到另一个数据点要走多远，越短越好）。 self-attention 复杂度，例如 queries?和 keys 长度是 n，它们的列数都是d，所以是? $n^{2} \cdot d$ ?，顺序性，因其就是几个矩阵乘法，矩阵乘法并行度较高，所以是? $O(1)$ ?的，最大的长度，一个 query 可以和所有的 keys 做运算，输出是所有 values 的加权和，所以任何一个 query 和任何一个很远的 key-value 对只需要一次就可以。循环层，复杂度，序列长度是 n ，维度是d，可以理解为过 n 次 dense layer ，就是 $O(n \cdot d ^{2})$ ?，对比 self-attention 若是 n 大则循环层复杂度低， d 大则 attention 复杂度低，现在看来 n 和 d 在差不多的数据层面所以这俩差不多复杂度，但是由于循环层需要一个一个做运算，下一步计算必须等前面步计算完成，所以并行化上比较亏，信息从第一个数据点到最后一个数据点要走 n 步，对长度比较长的序列不够友好，因为信息会走丢。卷积， kernel 是 k ， d 是输入输出的通道数， k 通常不会很大，一般就是3或5等类似，卷积的并行度比较高，卷积的一个点每一次是有一个长为 k 的窗口来看的，所以 k 距离以内的信息一次就能传递，但是超出 k ，需要一层一层的叠上去。self-attention（ restricted ）， query 只跟最近的 r 个邻居做运算，但是相对原先的自注意力机制信息从一个数据点到另一个数据点可能需要走更多的步数。attention 主要关心的是对于特别长的信息能把整个信息整合的更好，所以self-attention（ restricted ）不常用，还是原始的自注意力机制用的更广一点。

实际上， attention 对模型的假设更少，想要达到和 RNN 、 CNN 相同的效果则需要更大的模型和更多的数据，所以现在基于 transformer 的模型都是特别大特别贵。

实验

Training Data and Batching

在标准的WMT 2014 English-German数据集上进行了训练，其中包含约450万个句子对。这些句子使用?byte-pair encoding （BPE，把词根提出来，可以使整个字典比较小）进行编码，源语句和目标语句共享大约37000个 tokens 的词汇表（编码器和解码器的 embedding 就可以公用，模型会比较简单）。对于英语-法语翻译，我们使用更大的WMT2014 English-French 数据集，它包含3600万个句子，并将tokens分成32000个word-piece词汇表[38]。序列长度相近的句子一起进行批处理。每个训练批次的句子对包含大约25000个源tokens和25000个目标tokens。

Hardware and Schedule

我们在一台具有8个NVIDIA P100 GPU的机器上训练我们的模型。使用本文描述的超参数的base models，每个 batch 耗时约0.4秒。我们的base models共训练了10万步，花费12小时。如表3底部描述的大模型，?每个 batch 耗时约1.0秒，大模型训练了30万步（3.5天）。

Optimizer

使用Adam优化器，其中 $\beta_{1} = 0.9, \beta_{2}= 0.98$ ??（这边? $\beta_{2}$ ?取的比较小，常用的是0.999）及 $\epsilon = 10^{-9}$ ?。根据以下公式在训练过程中改变学习率：

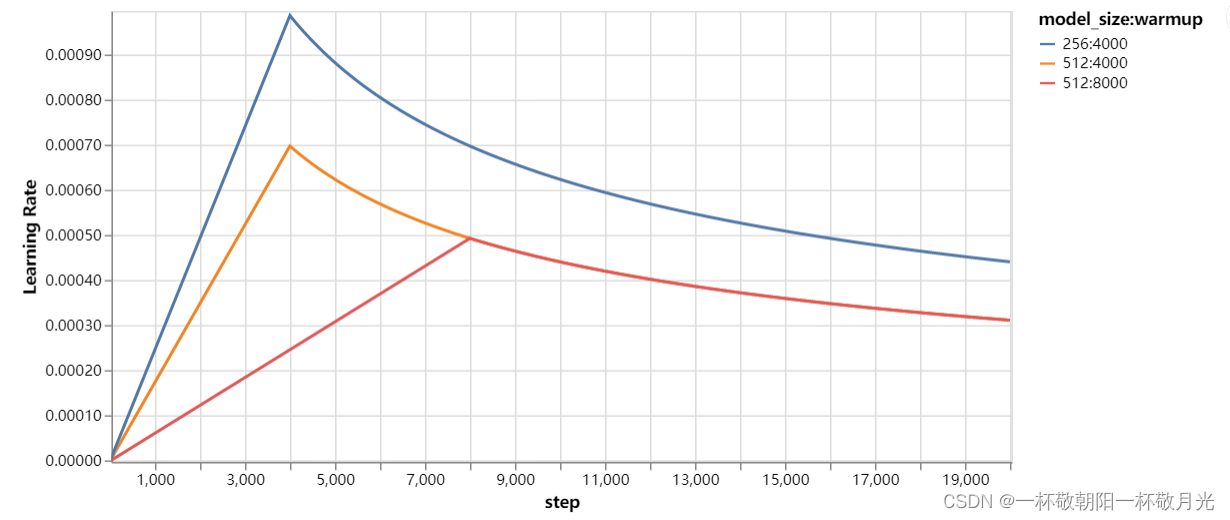
$l_{rate} = d_{model}^{-0.5} \cdot \min(step\_num^{-0.5}, step\_num\cdot warmup\_steps^{-0.5})$

这对应于在第一次warmup_steps?步骤中线性地增加学习速率，并且随后将其与步骤数的平方根倒数成比例地减小。我们使用warmup_steps?= 4000。学的向量越长的时候，学习率要低一点。先由一个较小的值慢慢爬到一个高的值，爬到之后按照步数的0.5次方衰减。这边几乎没啥可调的超惨，本来 adam 对学习率不怎么敏感。

下面直观感受一下，学习率的变化情况，蓝色的? $d_{model} = 256$ ?，其余的? $d_{model} = 512$ ?，从蓝色线和橙色线可以看出，大的? $d_{model}$ ?学习率要低一点。红色的? $warmup\_steps = 8000$ ?，其余的? $warmup\_steps = 4000$ ?，? $warmup\_steps$ ?越小，学习率一开始涨的越快，但是达到一个临界点后他们的学习率一样，毕竟过了? $warmup\_steps$ ?后，学习率就由第一部分决定。

Regularization

训练期间我们采用三种正则化：

Residual Dropout?将 dorpout 应用到每个子层的输出，在进入残差连接和 layerNorm 之前。此外，在编码器和解码器中，将dorpout应用到embeddings和位置编码求和。对于 base model ，我们使用 $P_{drop} = 0.1$ ?丢弃率，把10%的元素置成0，剩下的元素乘上1.1（? $1 / (1 - p)$ ）。可以看到对每一个带权重的层在输出上都使用了?dorpout 。

Label Smoothing?在训练过程中，我们使用的label smoothing的值为? $\epsilon_{ls}=0.1$ ??。这损害了perplexity，因为模型学得更加不确定，但提高了准确性和BLEU得分。

Results

结论

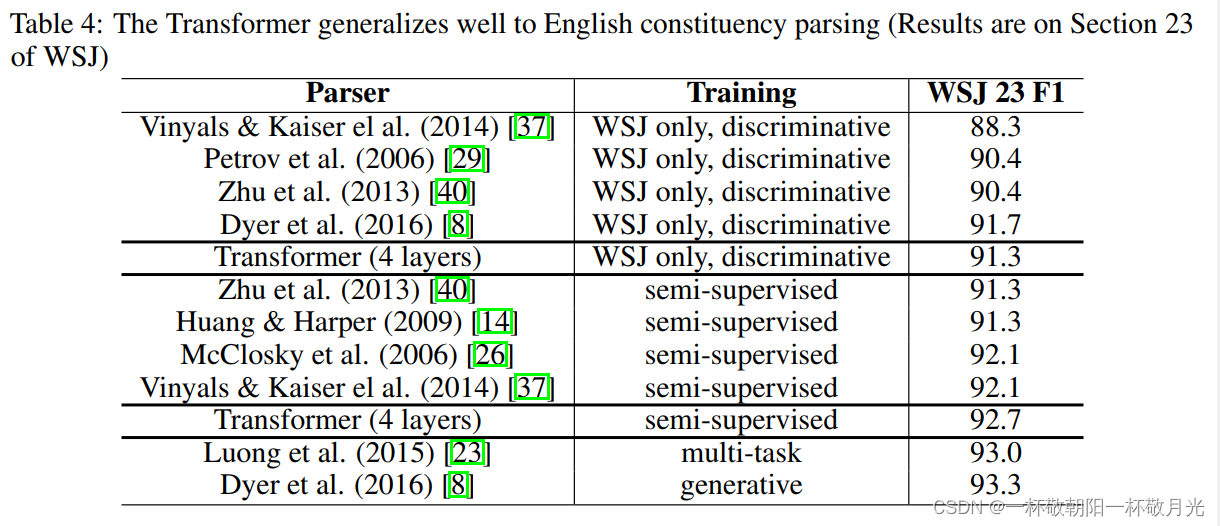
文中提出的 Transformer ，是第一个完全基于注意力机制的序列转录模型--将编码器-解码器架构常用的循环层替换成了multi-headed self-attention 。在机器翻译的任务上， Transformer 的训练要比比循环层卷积层快很多。在 WMT 2014 English-to-German 和?WMT 2014 English-to-French 翻译任务上，达到了最好的效果。在 WMT 2014 English-to-French 任务上，效果优于所有的模型，前一项任务甚至优于所有先前的集成模型。很看好基于注意力机制模型的前景，并打算运用到其他任务上。我们计划将 Transformer 扩展到涉及输入和输出模式的文本以外的任务上，并研究 local ,? restricted 注意机制，以有效处理图像、音频和视频等。 generation less sequential 也是一个研究方向。

附

batch norm VS layer norm

考虑二维输入的情况，每一行是样本，每一列是特征， batch norm 就一个列是每次在一个 batch 内将每（每一个特征）变成均值0方差1。训练阶段在小批量里面算出均值方差；算出全局的均值方差存起来在预测的时候用。还会学一个? $\lambda,\beta$ ? 出来，即可以把这个向量通过学习变为方差为某个值均值为某个值的东西。

同考虑二维输入， layer norm 在很多时候和 batch norm 是一样的，不过 layer norm 是对每个样本做了 normalization ，即把每一行变为均值0方差1的向量，可以认为是把矩阵转置一下，做一个? batch norm ，再转置回去。

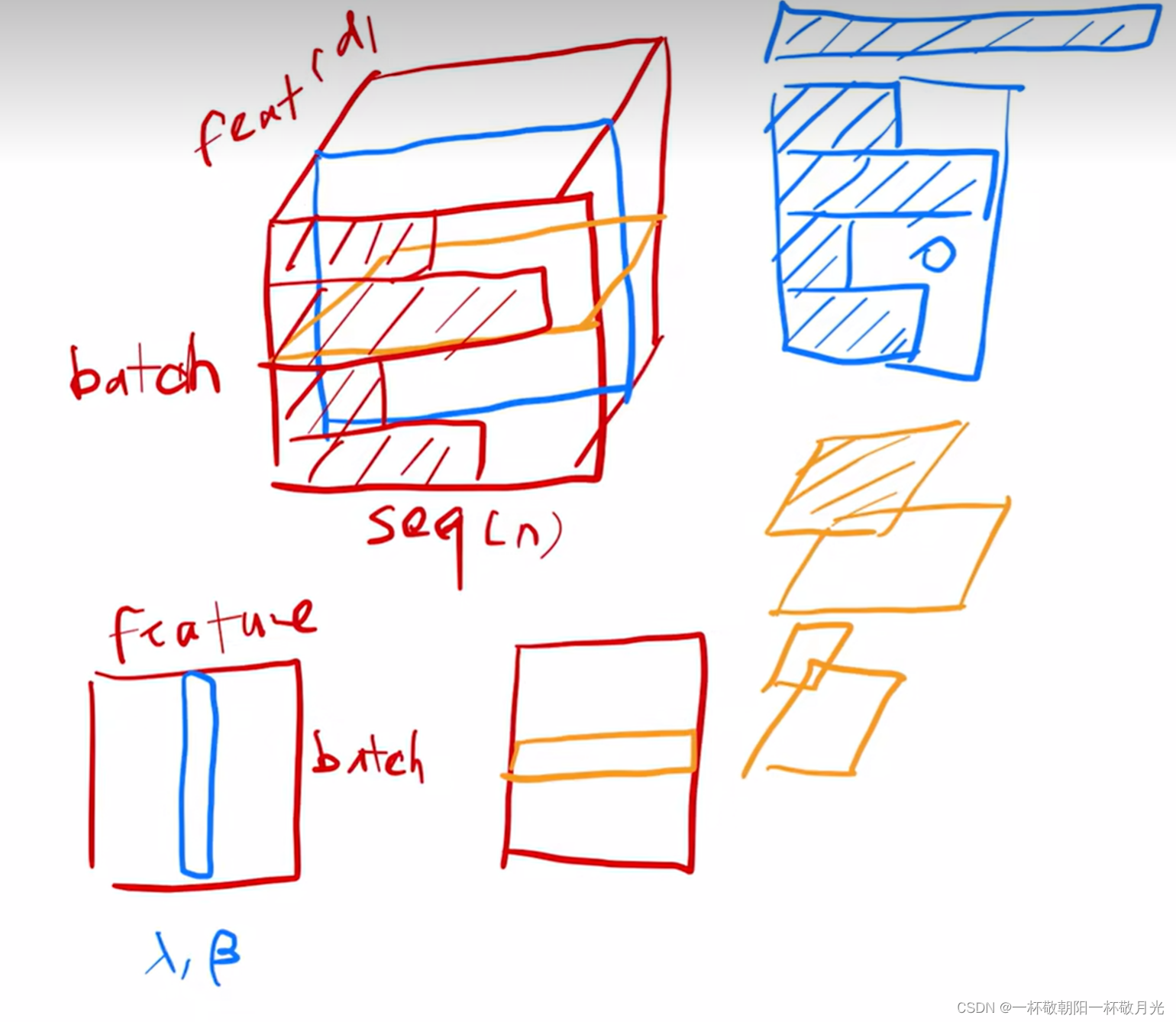
但是 transformer 里面的输入是三维的，输入的是一个序列的样本，每一个样本里面有很多个元素，每个元素有自己的 embedding ，形状是? $(batch\_size, seq\_len, d_{model})$ ? ，这时候若用 batch norm ，每次取一个特征，把他的序列的元素以及 batch 全部搞出来? $(batch\_size, seq\_len)$ ? 展平成一个向量? $(batch\_size \times seq\_size, )$ ? ，将其变为均值0方差1。 layer norm 是针对 hidden 层的，就是每次取一个样本一个词，把它的 embedding 全搞出来? $(d_{model},)$ ?? ，将其变为均值0方差1。对于这种变长的序列通常 layer norm 用的比较多，因为序列中每个样本的长度? $seq\_len$ ? 可能会发生变化，见图蓝色 batch norm ，黄色? layernorm ，没有值的地方通常补0，主要就是两种切法的不同，会带来计算均值方差的不同，若样本长度变化比较大，每次算一个 batch 里面的均值方差抖动相对较大，还有一点，预测的时候我们会记下全局的均值方差，若预测的样本比较长，我们在训练的时候没见到伸出去那么长的之前算出的均值方差不那么好用。 layernorm 是每一个样本的每一个词自己算均值方差，也不需要存下全局均值方差，毕竟是针对样本的，反正无论长短都是在各自样本里面算的，相对来说稳定一些。

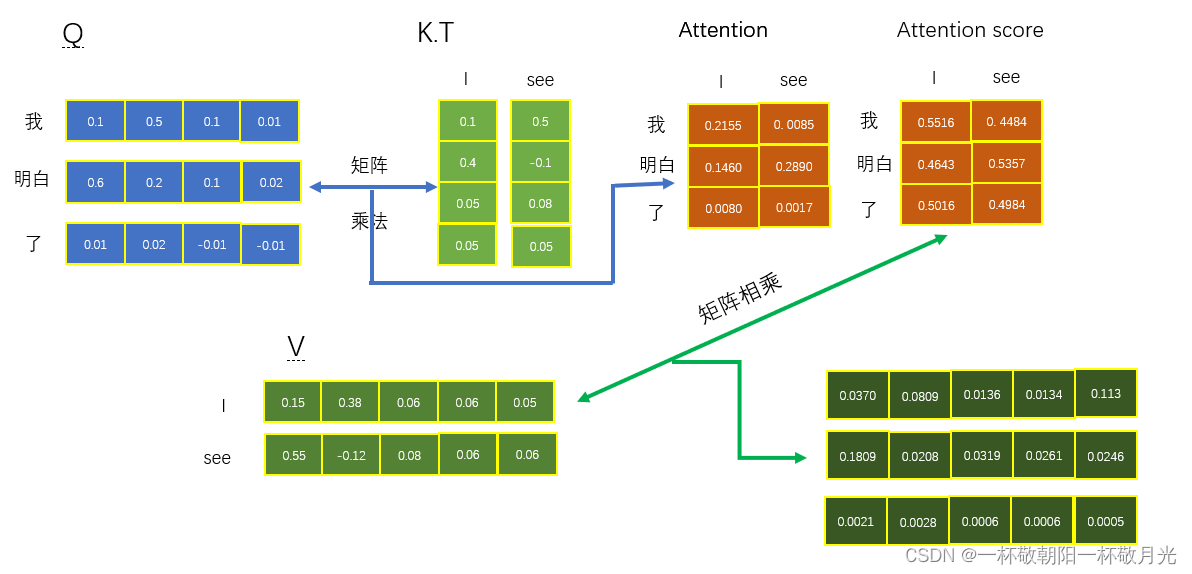
attention

Q = torch.tensor([[[0.1, 0.5, 0.1, 0.01], [0.6, 0.2, 0.1, 0.02], [0.01, 0.02, -0.01, -0.01]]])
K = torch.tensor([[[0.1, 0.4, 0.05, 0.05], [0.5, -0.1, 0.08, 0.05]]])
V = torch.tensor([[[0.15, 0.38, 0.06, 0.06, 0.05], [0.55, -0.12, 0.08, 0.06, 0.06]]])
att = torch.matmul(Q, K.transpose(-2, -1))
att_score = att.softmax(dim=-1)
out = torch.matmul(att_score, V)
print("Q: {}, K: {}, V: {}, att_score: {}, out: {}".format(
    Q.size(), tuple(K.size()), tuple(V.size()), tuple(att_score.size()), tuple(out.size())
))
print("att:")
print(att)
print("att_score:")
print(att_score)
print('out:')
print(out)

当用内积做相似度是，Q和K最后一维要相同，output是values的加权和（所以输出和? values 的最后一维相同），output倒数第二维是Q倒数第二维的维度，因为本来一个query，就是通过该query和所有的keys来算得相似度向量，该向量的元素个数是keys的个数，这些元素又是对应的values的权重，那么一个query会得到一个加权和，可以理解为该序列values在给定query下的表示。

Label Smoothing

关于 Transformer 中提到的 Label Smoothing ，参考论文?https://arxiv.org/pdf/1512.00567.pdf 中的?7. Model Regularization via Label Smoothing 。

标签平滑（?Label Smoothing ）通常用于分类问题，目的是防止模型在训练时过于自信地预测标签，进而改善泛化能力差的问题。

设? $K$ ?分类任务? $k \in \{1 \cdots K\}$ ?，有一个样本? $x$ ?，其真实标签是 y ，?真实标签分布用? $q(k)$ ?表示，后续用 Dirac delta $\delta _{k, y}$ ?来表示。

$\left\{\begin{matrix} q(k) = 1, & k = y\\ q(k) = 0, & k \neq y \end{matrix}\right.$

用? $p(k)$ ?表示预测分布，

$p(k) = e^{z_{k}} / \sum_{i=k}^{K} e^{z_i}$

交叉熵损失

$\l = H(q, p)= - \sum_{k=1}^{K} \log(p(k)) q(k)$

梯度，在-1 到 1 之间。

$\frac{\partial \l}{\partial z_{k}} = p(k) - q(k)$

因为只有 k=y 时， $q(k)$ ?才为1，所以交叉熵损失只关心正确标签，即只会最大化正确标签的最大似然，也就是? $\l =- \log(p(y))$ ?，对于有限值? $z_{k}$ ?来说，对所有的 $k \neq y$ ?有? $z_{y} \gg z_{k}$ ?时可以近似达到正确标签的最大似然。这会产生两个问题。1. 导致过拟合：若模型将所有的可能性全给到正确标签，不利于泛化。2. 模型会鼓励正确标签的预测值相对于其他的预测值的差异过大，鼓励模型在目标类别处预测的概率趋近1，非目标类别的概率趋近0，即最终预测的logits向量中目标类别? $z_{y}$ ?的值会趋近无穷大，使模型向预测正确与错误标签的 logit 差值无限增大的方向学习（此时梯度也接近0），而过大的 logit 差值会使模型缺乏适应性，对它的预测过于自信。

标签平滑鼓励模型不那么自信，这可能不是最大化训练标签似然函数所期望的，但是可以很好的对模型起到正则化，增加鲁棒性。取平滑参数? $\epsilon$ ?，分布 $u(k)$ ?。将真实的标签分布? $q(k|x) = \delta_{k,y}$ ?替换成下面的分布，以权重? $1-\epsilon$ ?和权重? $\epsilon$ ?分别融合了真实标签分布? $q(k)$ 和选定的固定分布? $u(k)$ 。

? $q^{'} (k | x) = ( 1 - \epsilon ) \delta_{k, y} + \epsilon u(k)$

若选取均匀分布，即? $u(k) = 1/ k$ ?，给正确标签先分配? $1-\epsilon$ 的分数，将剩下的权重? $\epsilon$ 均摊到所有的的标签上，则正确标签权重? $1-\epsilon + \epsilon / K$ ?，其它的非正确的标签都分配了? $\epsilon / K$ ?：