研究内容
- 许多基于GCN的知识图补全( KGC )模型首先使用GCN聚合邻居实体和关系信息生成实体和关系的表示,然后使用知识图嵌入(KGE)模型捕获实体和关系之间的交互。这一操作虽然引入了额外的计算复杂性,但其性能无法超过最先进的KGE模型
- 作者通过消融实验证明,GCN中的图结构建模对KGC模型的性能没有显著影响,对于实体表示的线性转换的作用更大一些
- 作者设计了简单的LTEKGE模型,对实体表示施加类似的线性转换之后, 性能与GCN模型相差无几
符号定义
- 知识图谱表示为 K = { ( e i , r j , e k ) } ? E × R × E \mathcal{K}=\left\{\left(e_i, r_j, e_k\right)\right\} \subset \mathcal{E} \times \mathcal{R} \times \mathcal{E} K={(ei?,rj?,ek?)}?E×R×E,可以由一个三阶邻接张量 X ∈ { 0 , 1 } ∣ E ∣ × ∣ R ∣ × ∣ E ∣ \mathcal{X} \in\{0,1\}^{|\mathcal{E}| \times|\mathcal{R}| \times|\mathcal{E}|} X∈{0,1}∣E∣×∣R∣×∣E∣唯一确定
- 给定三元组
(
h
i
,
r
j
,
t
k
)
∈
E
×
R
×
E
\left(h_i, r_j, t_k\right) \in \mathcal{E} \times \mathcal{R} \times \mathcal{E}
(hi?,rj?,tk?)∈E×R×E,KGC定义一个得分函数
s
:
E
×
R
×
E
→
R
s:\mathcal{E} \times \mathcal{R} \times \mathcal{E} \rightarrow \mathbb{R}
s:E×R×E→R以获得三元组成立的分数
s
(
h
i
,
r
j
,
t
k
)
s\left(h_i, r_j, t_k\right)
s(hi?,rj?,tk?),有效三元组的得分应高于无效三元组,一些有代表性的得分函数定义如下
- TransE: f ( h , r , t ) = ? ∥ h + r ? t ∥ 1 / 2 f(h, r, t)=-\|\mathbf{h}+\mathbf{r}-\mathbf{t}\|_{1 / 2} f(h,r,t)=?∥h+r?t∥1/2?
- DistMult: f ( h , r , t ) = h ? R t f(h, r, t)=\mathbf{h}^{\top} \mathbf{R t} f(h,r,t)=h?Rt
- ConvE: f ( h , r , t ) = σ ( vec ? ( σ ( [ r  ̄ , h  ̄ ] ? ω ) ) W ) ? t f(h, r, t)=\sigma(\operatorname{vec}(\sigma([\overline{\mathbf{r}}, \overline{\mathbf{h}}] * \omega)) W)^{\top} \mathbf{t} f(h,r,t)=σ(vec(σ([r,h]?ω))W)?t
研究对象
- 论文研究了三种有代表性的模型,包括Relational-GCN (RGCN)、 Weighted-GCN (WGCN)和CompGCN。其中CompGCN是目前效果最好的GCN模型,在FB和WN数据集上能达到0.355和0.479的MRR,但最佳的KGE模型ComplEx+N3可以达到0.366和0.489
- 嵌入更新过程包括三个阶段:1)从图邻域聚合信息 2)实体表示的转换 3)关系表示的转换,三个模型的区别如下表
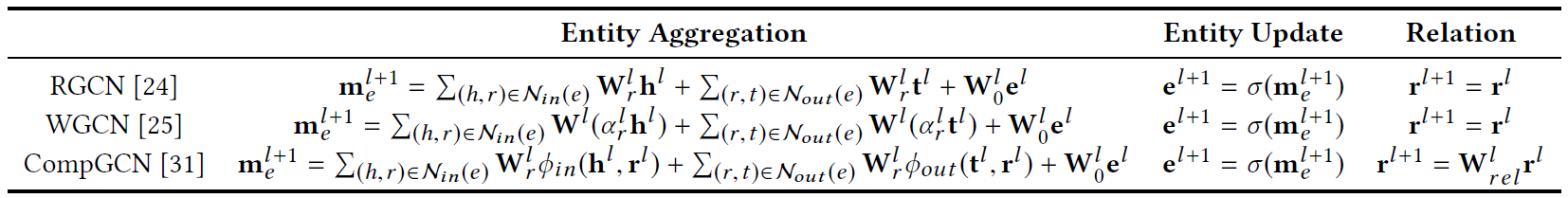
实验设置
- TransE、DistMult和ConvE(简称T、D、C)作为解码器
- 使用二元交叉熵(BCE)损失函数
L = 1 ∣ S ∣ ∑ ( h , r , ? ) ∈ S ( 1 ∣ E ∣ ∑ t ∈ E y ( h , r , t ) ? log ? f ( h , r , t ) + ( 1 ? y ( h , r , t ) ) ? log ? ( 1 ? f ( h , r , t ) ) ) L =\frac{1}{|S|} \sum_{(h, r, \cdot) \in S}(\frac{1}{|\mathcal{E}|} \sum_{t \in \mathcal{E}} y(h, r, t) \cdot \log f(h, r, t) +(1-y(h, r, t)) \cdot \log (1-f(h, r, t))) L=∣S∣1?(h,r,?)∈S∑?(∣E∣1?t∈E∑?y(h,r,t)?logf(h,r,t)+(1?y(h,r,t))?log(1?f(h,r,t))) - 数据集为FB15k237和WN18RR
- 使用MR,MRR和 H@N作为评估指标。较低的MR和较高的MRR/H@N表明性能更好
Do GCNs Really Bring Performance Gain?
- 作者首先复现了几个目标模型并取得了更好的效果,“O”表示结果取自他们的原始论文,而“R”表示使用DGL复制结果
- 在大多数情况下,GCN显著提高了KGE模型的性能,但并非所有GCN都能提高所有KGE模型的性能
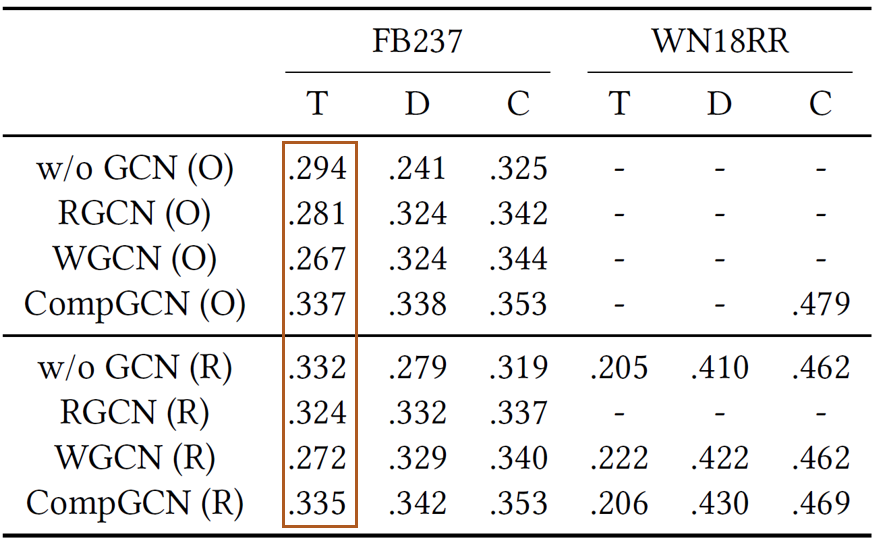
- 单个GCN层就足以实现令人满意的性能
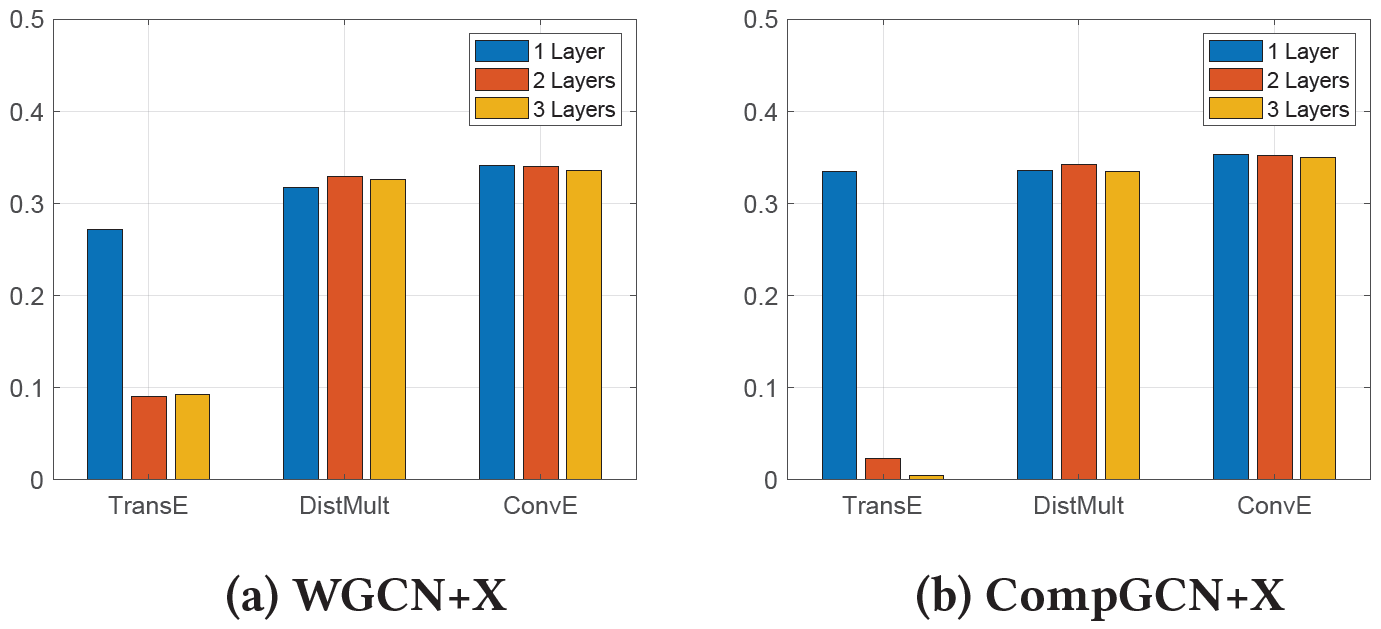
Which Factor of GCNs is Critical in KGC?
图结构建模
- RAT操作:随机断开邻接张量,即在消息传播步骤将邻居实体替换为随机实体
- WNI操作:完全不使用邻居信息,相当于图中没有边,自己更新自己的表示
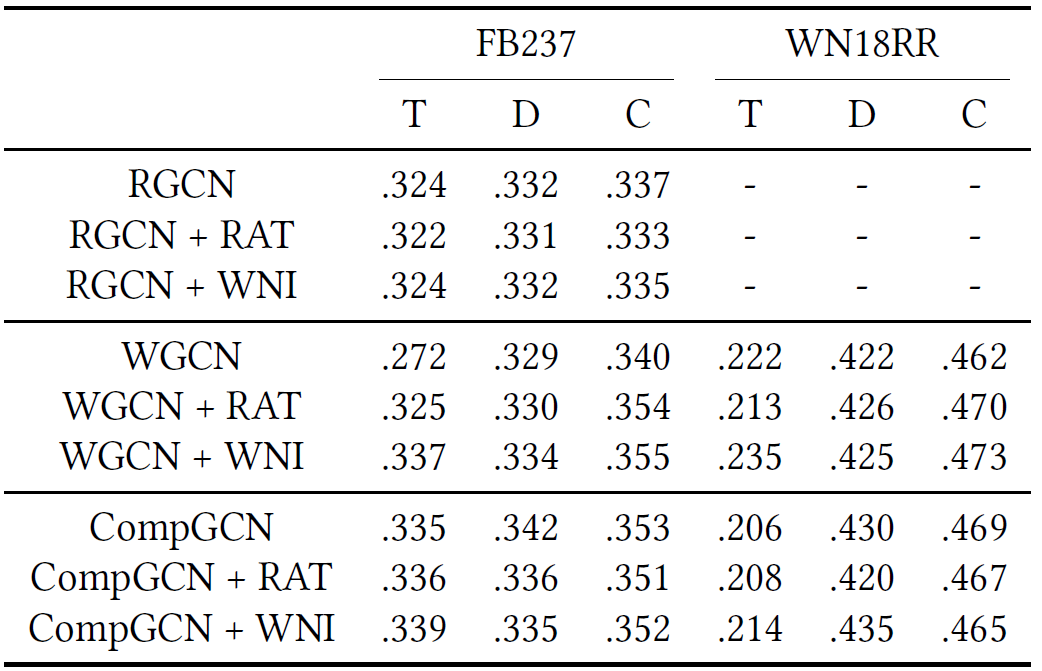
结果表明,尽管GCN编码器可以提高KGE模型的性能,但GCN中的图结构建模对于性能的提高并不重要,性能增益并非来自邻域聚合
自环信息
WSI操作: 去除自环信息,实体的表示仅基于其邻域实体和关系的表示生成
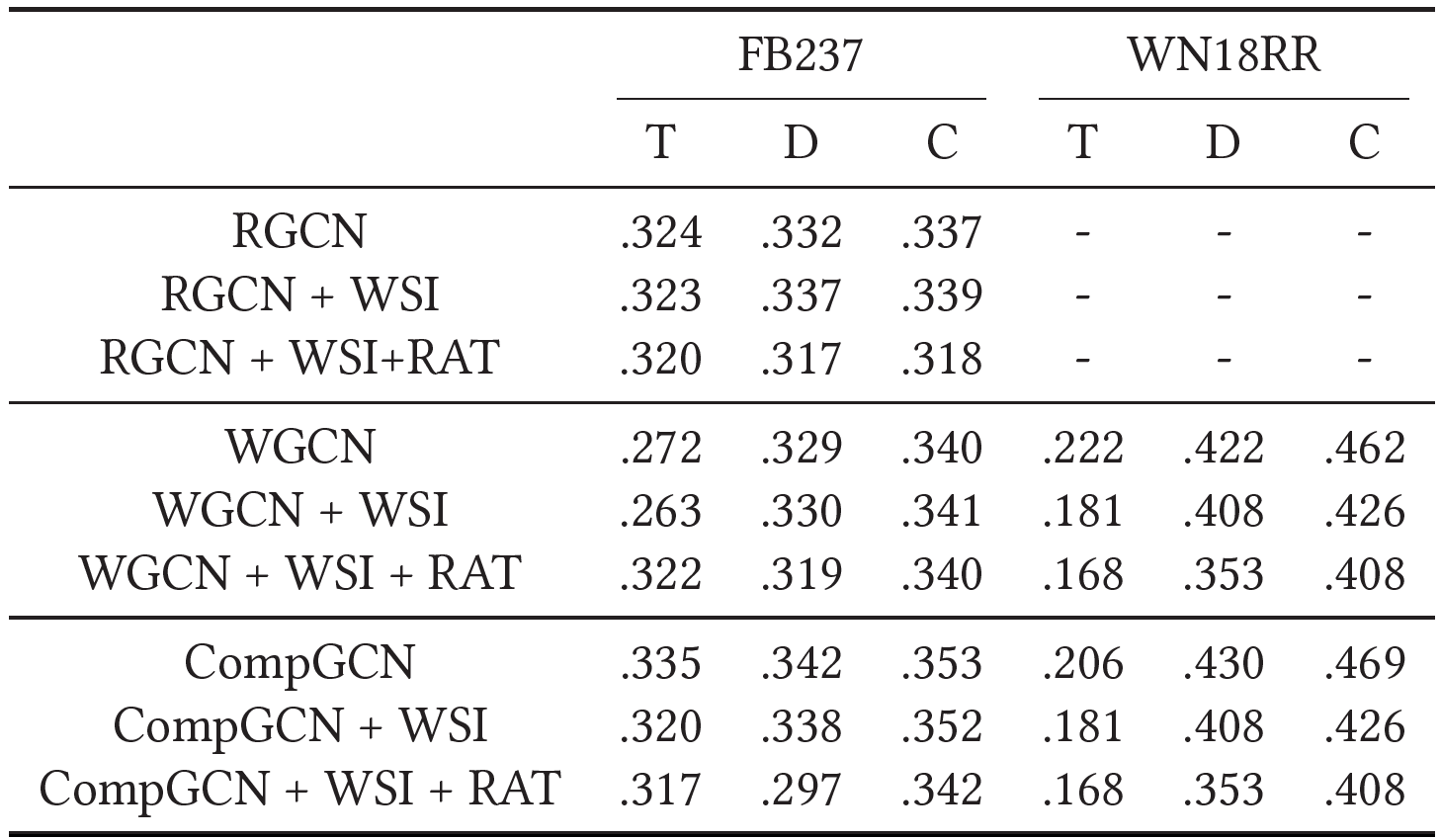
- 目前的三个变体:1)仅使用自环信息 2) 仅使用邻居信息 3) 仅使用随机生成的邻居信息 都被证明对效果影响不大
- 论文认为这三个变体都有一个共同点,即它们能够以高置信度区分具有不同语义的实体。如果只使用自环信息,则每个实体的表示是独立的,因此可以区分。如果只使用邻居信息,那么只有当两个实体具有相似的邻居表示时,它们才会具有相似的表示(仅使用邻居信息(WSI/WSI+RAT)的性能远低于基于WN18RR的完整GCN模型。这是合理的,因为WN18RR和FB15k-237中相邻实体的平均数量分别为2.1和18.7。基于较少的相邻实体来区分具有不同语义的实体更具挑战性)。不过论文没有分析第三种情况,我猜测可能是随机替换的概率不是很大,类似于dropout,保留了一大部分邻居信息
论文提出了一种假设:如果聚合过程能够很好地区分具有不同语义的实体,则GCN可以提高KGE模型的性能。为证明这一点,论文做了控制是否使用自环信息,同时随机抽样给定实体集中的邻居的实验。随着集合的数目变小,不同实体的邻域越来越相似,使得它们难以区分。但如果引入自环信息,则基本没有下降。
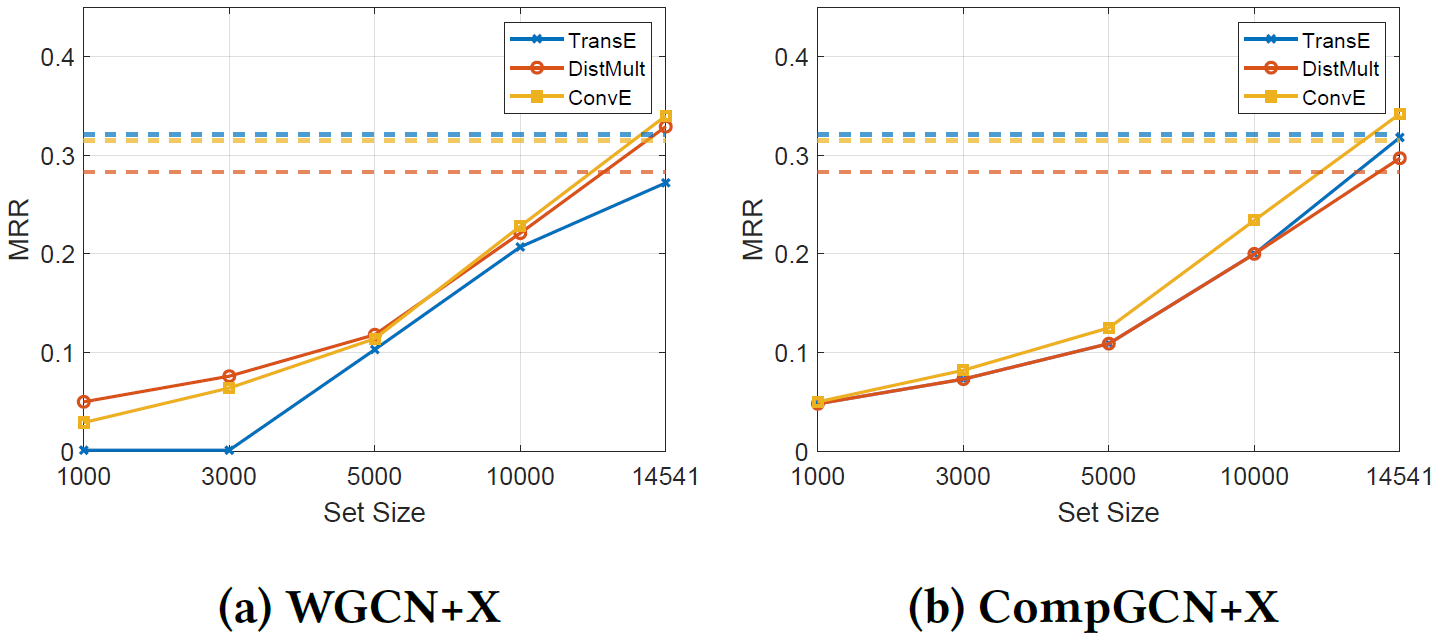
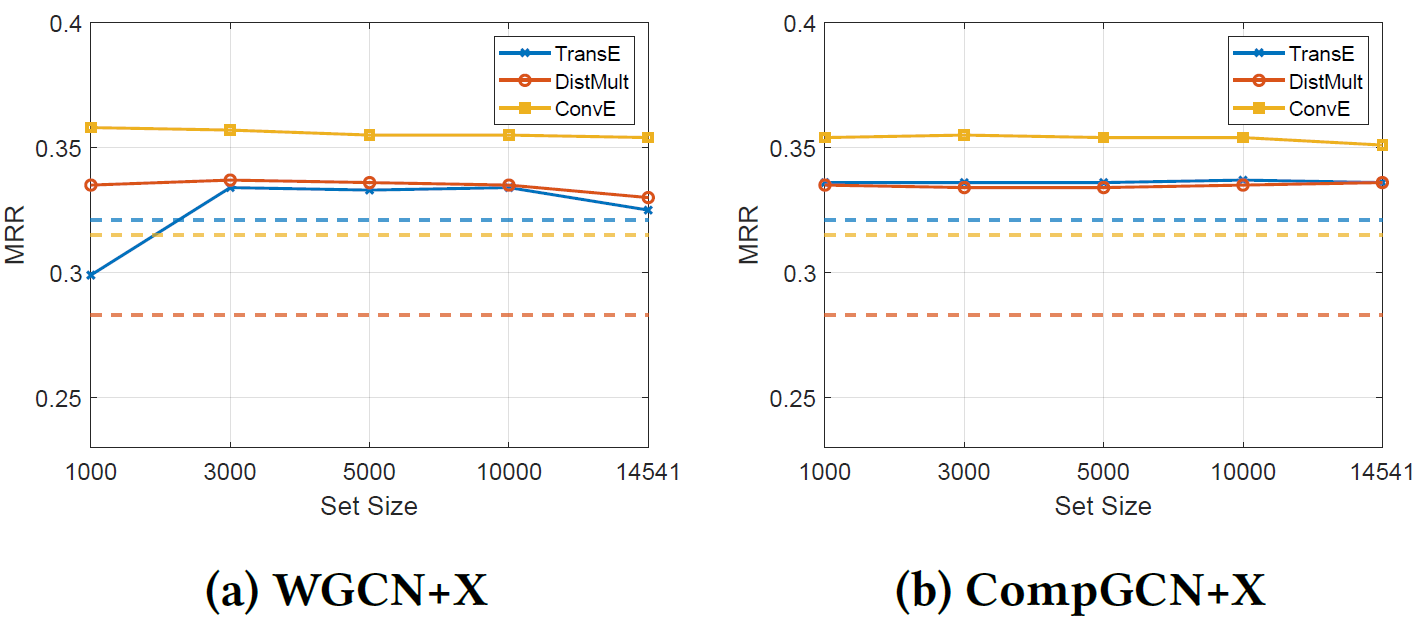
关系的线性转换
LTR:CompGCN对关系的线性变换,消融实验表明这一块也不重要。由于嵌入更新步骤中的两个部分都被证明不重要,因此聚合实体表示的转换对于性能改进至关重要。
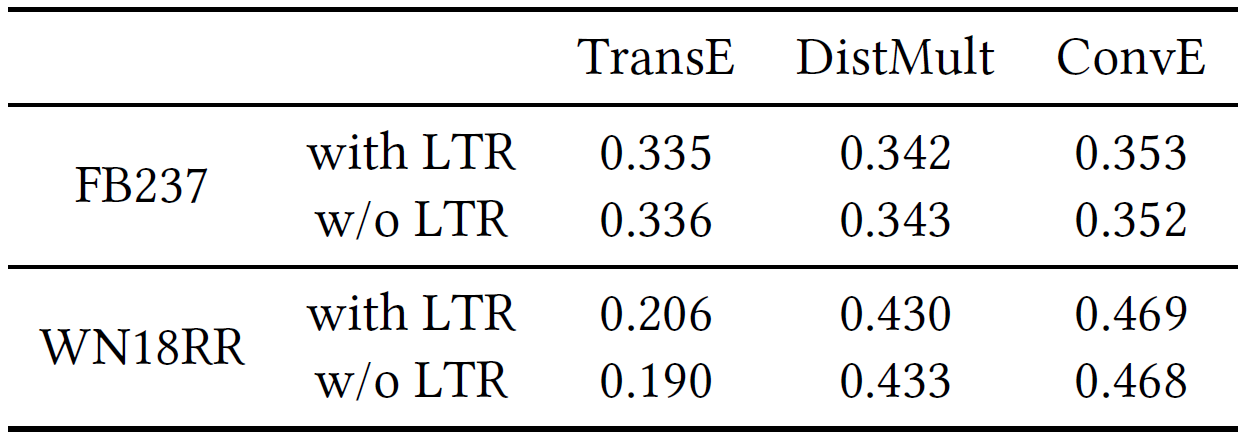
得出结论:只要GCN能够通过生成的实体表示很好地区分具有不同语义的实体,实体表示的转换就可以有效地提高KGE模型的性能。
LTE-KGE
论文认为现有的复杂GCN对于KGC可能是不必要的,因此提出LTE-KGE以证明更简单的模型可以实现与基于最新GCN的模型相似的性能
-
假设三元组 ( h , r , t ) (h, r, t) (h,r,t)的原始得分函数为 f ( h , r , t ) f(\mathbf{h}, \mathbf{r}, \mathbf{t}) f(h,r,t),LTE-KGE将其修改为 f ( g h ( W h h ) , r , g t ( W t t ) ) ) \left.f\left(g_h\left(W_h \mathbf{h}\right), \mathbf{r}, g_t\left(W_t \mathbf{t}\right)\right)\right) f(gh?(Wh?h),r,gt?(Wt?t)))
-
LTE-KGE可以理解为一个加强版的只使用自环信息的GCN,其中 g h g_h gh?和 g t g_t gt?是恒等函数,非线性激活函数,批量归一化,dropout等操作的任意组合
-
论文在实验中令 W h W_h Wh?和 W t W_t Wt?共享参数, g h g_h gh?和 g t g_t gt?对于TransE设为恒等函数,对于DistMult/ConvE设为BN+dropout
效果与时间对比
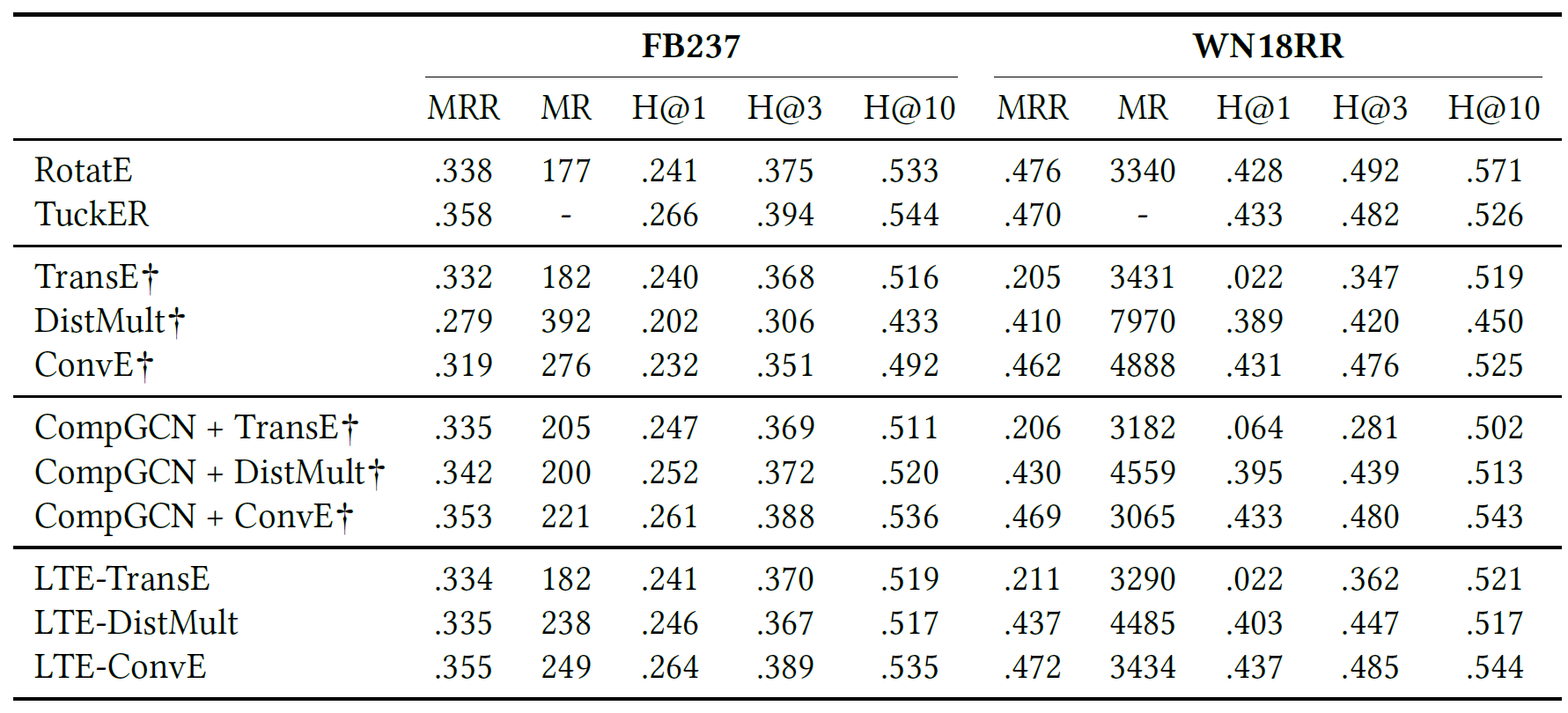
LTE-KGE & GCN
这一部分主要想说明LTE-KGE已经隐式聚合了邻居信息
给定头实体 h h h,目标是最小化所有与之相连的邻居的损失
∑ r ∈ R h ∑ t : ( h , r , t ) ∈ S log ? f ( W h , r , W t ) \sum_{r \in R_h} \sum_{t:(h, r, t) \in S} \log f(W \mathbf{h}, \mathbf{r}, W \mathbf{t}) r∈Rh?∑?t:(h,r,t)∈S∑?logf(Wh,r,Wt)
其关于 h \mathbf{h} h的梯度为
∑ r ∈ R h ∑ t : ( h , r , t ) ∈ S 1 f ( W h , r , W t ) ? f ? h ( W h , r , W t ) \sum_{r \in R_h} \sum_{t:(h, r, t) \in S} \frac{1}{f(W \mathbf{h}, \mathbf{r}, W \mathbf{t})} \frac{\partial f}{\partial \mathbf{h}}(W \mathbf{h}, \mathbf{r}, W \mathbf{t}) r∈Rh?∑?t:(h,r,t)∈S∑?f(Wh,r,Wt)1??h?f?(Wh,r,Wt)
对LTE-TransE、LTE-DistMult和LTE-ConvE分别求梯度,可归纳为以下形式,可以看到梯度实质上是计算了邻居信息的聚合,用梯度来更新 h \mathbf{h} h自然等同于一层GCN迭代
∑ r ∈ R h ∑ t : ( h , r , t ) ∈ S a ( h , r , t ) W t + b ( h , r , t ) \sum_{r \in R_h} \sum_{t:(h, r, t) \in S} a(\mathbf{h}, \mathbf{r}, \mathbf{t}) W \mathbf{t}+b(\mathbf{h}, \mathbf{r}, \mathbf{t}) r∈Rh?∑?t:(h,r,t)∈S∑?a(h,r,t)Wt+b(h,r,t)